Mở rộng: Bài toán tổng quát của bài toán trên có thể quy về bài toán sau:
Cho $a_i>0$ ($i=1,2,3,...,n$) với $a_1a_2...a_n=1$
Tìm GTLN của:
$A=\sum \frac{1}{a_{n}^k\left (a_1^{n+k(n-1)}+a_2^{n+k(n-1)}+..+a_{n-1}^{n+k(n-1)} \right )+1}$
Giả sử $a_1\geq a_2\geq .....\geq a_n$
Áp dụng chebyshev và AM-GM ta có:
$S=a_1^{n+k(n-1)}+a_2^{n+k(n-1)}+..+a_{n-1}^{n+k(n-1)}\geq \frac{1}{n-1}(a_1+a_2+..+a_{n-1})(\sum_{i=1}^{n-1} a_i^{(n-1)(k+1)})$
$S\geq (a_1+a_2+..+a_{n-1})(a_1a_2..a_{n-1})^{k+1}$
Áp dụng tương tự rồi áp dụng vào A ta có:
$A\leq \sum \frac{a_n}{a_1+a_2+..+a_n}=1$
Dấu bằng xảy ra khi $a_1=a_2=..=a_n=1$

_______________
Điểm mở rộng: $d_{mr}=10$

Cho $a,b,c>0$ và $abc=1$ . Tìm GTLN của biểu thức
$$A=\sum \frac{1}{\sqrt{a^{5}c+b^{5}c+1}.\sqrt{b^{5}a+c^{5}a+1}}$$

Toán thủ ra đề
19kvh97

Ta có:
$(a-b)^2(a+b)(a^2+ab+b^2)\geq 0$
$\Leftrightarrow a^5+b^5\geq a^2b^2(a+b)$
Áp dụng tương tự ta suy ra:
$A\leq \sum\frac{1}{\sqrt{ab(a+b)+1}.\sqrt{bc(b+c)+1}}$
$\Leftrightarrow A\leq \sum\frac{1}{\sqrt{ab(a+b)+abc}.\sqrt{bc(b+c)+abc}}$
$\Leftrightarrow A\leq \frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}{a+b+c}\leq 1$
(Do $\sqrt{ab}+\sqrt{ac}+\sqrt{bc}\leq a+b+c$ )
Vậy GTLN của A là 1 khi $a=b=c=1$
________________________
*Lưu ý: Bài làm khá vắn tắt, cần chú thích rõ ràng hơn (VD: theo AM-GM)
Điểm bài làm $d=10$
$S=\left\lfloor\dfrac{52-1}{2}\right\rfloor+3\times 10+10=65$

Định $a$ để hệ phương trình sau có nghiệm duy nhất, tìm nghiệm ấy:

$$\left\{\begin{matrix} ax^{2}+a-1=y-|\sin x|\\ \tan ^{2}x+y^{2}=1 \end{matrix}\right.$$
Toán thủ ra đề:
hoangtrong2305

ĐK: $x\neq \frac{\pi}{2}+k\pi$ ($k\in Z$)
Nhận xét: nếu phương trình có nghiệm $x=x_0$ khác 0 thì cũng có nghiệm $x=-x_0$
Khi đó PT có ít nhất 2 nghiệm..
Do đó để PT có nghiệm duy nhất thì điều kiện cần là $x=0$
Thay x=0 vào ta được:
$\left\{\begin{matrix} a-1=y\\ y^2=1 \end{matrix}\right.$
Khi đó ta có 2 số a thỏa mãn là $a=2$ và $a=0$
Ta xét điều kiện đủ
TH1: Với a=2 ta được:
$\left\{\begin{matrix} 2x^2+1=y-|sinx|\\ tan^2x+y^2=1 \end{matrix}\right.$
Từ PT số 2 của hệ suy ra $y\leq 1$ .. Do đó ta có $VT(pt1)\geq VP(pt1)$
Dấu bằng xảy ra khi $y=1, x=0$. Đây là nghiệm suy nhất của hệ
Vậy a=2 thỏa mãn.
TH2: Với a=0 ta có:
$\left\{\begin{matrix} -1=y-|sinx|\\ tan^2x+y^2=1 \end{matrix}\right.$
Thế $y=|sinx|-1$ vào PT dưới và đặt $t=|sinx|$ ($t\geq 0$) ta được PT
$t^4-2t^3-2t^2+2t=0$
Suy ra t=0 hoặc $t^3-2t^2-2t+2=0$ (1)
Xét $f(t)=VT(1)$
Ta có: $f(0).f(1)=-2<0$
Suy ra PT có nghiệm $t\in (0;1)$
Do đó PT có nghiệm $x\neq 0$ thỏa mãn..
Do đó PT có nhiều hơn 1 nghiệm.
Vậy a=0 không thỏa mãn.
KẾT LUẬN: PT đã cho có nghiệm duy nhất $x=0, y=1$ khi a=2
__________________________________
Điểm bài làm: $d=10$
$S=\left\lfloor\dfrac{52-1}{2}\right\rfloor+3\times 10+0+0=55$

Mình nghĩ là bài bạn chưa đúng.Theo mình thì:
Nếu ta lập được 1 tổ thì tổ thứ 2 thỏa mãn điều kiện đề bài
Xét tổ có 1 học sinh giỏi,số cách chọn học sinh giỏi là $3$
TH1: có $2$ học sinh khá,số cách chọn hs khá là $C^{2}_{5} \Rightarrow $ số cách chọn hs TB là $C^{5}_{8} \Rightarrow $ có : $3.C^{2}_{5}.C^{5}_{8}=1680$ cách chọn
TH2: có $3$ học sinh khá ,số cách chọn hs khá là $C^{3}_{5} \Rightarrow $ só cách chọn hs TB là $C^{4}_{8} \Rightarrow $ có $ 3.C^{3}_{5}.C^{4}_{8}=2100$ cách chọn
$\Rightarrow$ có tất cả :$3780$ cách chọn.

Mình nghĩ là bài bạn chưa đúng.Theo mình thì:
Nếu ta lập được 1 tổ thì tổ thứ 2 thỏa mãn điều kiện đề bài
Xét tổ có 1 học sinh giỏi,số cách chọn học sinh giỏi là $3$
TH1: có $2$ học sinh khá,số cách chọn hs khá là $C^{2}_{5} \Rightarrow $ số cách chọn hs TB là $C^{5}_{8} \Rightarrow $ có : $3.C^{2}_{5}.C^{5}_{8}=1680$ cách chọn
TH2: có $3$ học sinh khá ,số cách chọn hs khá là $C^{3}_{5} \Rightarrow $ só cách chọn hs TB là $C^{4}_{8} \Rightarrow $ có $ 3.C^{3}_{5}.C^{4}_{8}=2100$ cách chọn
$\Rightarrow$ có tất cả :$3780$ cách chọn.

Ừ, mình nhầm mất.. 2 tổ này là giống nhau chứ ko phân biệt nên không thể hoán vị được!!

Em có cách này ko biết đúng ko!
Áp dụng CT $(n+1)C_n^k=(k+1)C_{n+1}^{k+1}$ ta có:
$S=n(C_n^0.C_n^1+...+C_{n-1}^{n-1}.C_n^n)$
Ta quy về bài toán sau: Có n bi đỏ và n-1 bi xanh.. Tính số cách chọn n-1 viên bi từ 2n-1 viên bi đó:
Dễ thấy số cách chọn là $C_{2n-1}^n$
Mặt khác ta có thể tính như sau:
TH1: 0 bi xanh và n-1 bi đỏ có $C_{n-1}^0.C_n^{n-1}=C_{n-1}^0.C_n^1$
TH2: 1 bi xanh và n-2 bi đỏ có $C_{n-1}^1.C_n^2$
......
TH(n-1): n-1 bi xanh và 0 bi đỏ có $C_{n-1}^{n-1}.C_n^n$
Do đó:
$S=nC_{2n-1}^{n-1}$

Trong số 16 học sinh có 3 học sinh giỏi, 5 khá, 8 trung bình. Có bao nhiêu cách chia số học sinh đó thành hai tổ, mỗi tổ có 8 học sinh sao cho mỗi tổ đều có học sinh giỏi và mỗi tổ có ít nhất hai học sinh khá.

Bước đầu tiên xử lí cái đk:
Chọn 1 học sinh giỏi vào tổ 1 có 3 cách, chọn 1 học sinh giỏi vào tổ 2 có 2 cách
Chọn 2 học sinh khá vào tổ 1 và 2 học sinh vào tổ 2 có $C_5^2.C_3^2$ cách
Bây giờ thì xếp bừa vào là thỏa mãn.. Xếp 5 học sinh vào tổ 1 và 5 còn lại vào 2 có $C_{10}^5$ cách
Vậy có tất cả: $3.2.C_5^2.C_3^2.C_{10}^5$
Vừa nghĩ ko biết "chặt" chưa!!

Tìm hệ số của số hạng chứa $x^2$ trong khai triển nhị thức Niu-tơn của ${\left( {\sqrt x + \frac{1}{{2\sqrt[4]{x}}}} \right)^n}$, biết rằng $n$ là số nguyên dương thỏa mãn: \[2C_n^0 + \frac{{{2^2}}}{2}C_n^1 + \frac{{{2^3}}}{3}C_n^2 + .... + \frac{{{2^{n + 1}}}}{{n + 1}}C_n^n = \frac{{6560}}{{n + 1}}\]

Bài này chắc chỉ cần tìm n!!
Ta có công thức sau:
$(n+1)C_n^k=(k+1)C_{n+1}^{k+1}\Leftrightarrow \frac{1}{k+1}C_n^k=\frac{C_{n+1}^{k+1}}{n+1}$
ÁP dụng ta có:
$\frac{6560}{n+1}=\frac{1}{n+1}(2.C_{n+1}^1+2^2.C_{n+1}^2+..+2^{n+1}C_{n+1}^{n+1})$
$\Leftrightarrow 3^{n+1}-1=6560$
$\Leftrightarrow n=7$

Tính tích phân:
$$\int_{0}^{1}\left (x^2.e^{x^3}+\frac{\sqrt[4]{x}}{1+\sqrt{x}} \right )dx$$
Toán thủ ra đề:
luuxuan9x

Ta có:
$I=\int_{0}^1(x^2e^{x^3}+\frac{\sqrt[4]{x}}{1+\sqrt{x}})dx$
$=\frac{1}{3}\int_{0}^1(3x^2.e^{x^3})dx+\int_{0}^1(\frac{\sqrt[4]{x}}{1+\sqrt{x}})dx$
**Ta có:
$=\frac{1}{3}\int_{0}^1(3x^2e^{x^3})dx=\frac{1}{3}\int_{0}^1e^udu$ ( Với $u=x^3$)
Chú ý cách trình bày
$=\frac{e-1}{3}$
** Xét :
$\int_{0}^1\frac{\sqrt[4]{x}}{1+\sqrt{x}} dx$
đặt $x=t^4$ suy ra $dx=4t^3dt$
Thay vào ta có:
$\int_{0}^1\frac{\sqrt[4]{x}}{1+\sqrt{x}} dx=\int_{0}^1\frac{4t^4}{1+t^2}dt$
$=4\int_{0}^1(t^2-1+\frac{1}{1+t^2})dt$
$=4(\frac{-2}{3}+\left.\begin{matrix} arctan(t) \end{matrix}\right|_{0}^{1}) =\pi-\frac{8}{3}$
Do đó:
$I=\frac{e}{3}+\pi-3$

Hàm lượng giác ngược không được học trong chương trình nữa rồi
Điểm bài 9
S=25+3x9 = 52

Mở rộng 2: Tổng quát cho nhiều số.
Từ 10 chữ số $0,1,2,...,9$ có thể lập được bao nhiêu số tự nhiên có $S=\sum_{i=1}^{10}a_i$ (chữ số) sao cho các số $0,1,2,...,9$ xuất hiện đúng $a_1, a_2,..., a_{10}$ lần theo thứ tự.
Lời giải:
Coi các chữ số xếp theo thứ tự vào $S$ ô
B1: Xếp $a_1$ chữ số 0 vào $a_1$ ô trong $S-1$ ô cuối có $C_{S-1}^{a_1}$
B2 xếp lần lượt các số còn lại vào có $C_{S-a_1}^{a_2}.C_{S-a_1-a_2}^{a_3}....C_{a_{10}}^{a_{10}}$ cách
Kết luận: Số các số thỏa mãn là: $C_{S-1}^{a_1}.\prod_{i=1}^9 C_{S-a_1-a_2-..-a_i}^{a_{i+1}}$

$=\dfrac{(S-1)!(S-a_1)}{a_1!a_2!...a_{10}!}=\dfrac{(a_1+a_2+...+a_{10}-1)!(a_2+a_3+...+a_{10})}{a_1!a_2!...a_{10}!}$
_________
Mở rộng đúng!

$d_{mr_2}=10$

Mở rộng: Xét bài toán mở rộng cho bài toán trên:
Từ 8 chữ số $0,1,2,....,7$ có thế lập được bao nhiêu số tự nhiên có $8+k-1$ chữ số ($k\geq 1$) sao cho chữ số 6(hoặc có thể chữu số khác) xuất hiện k lần.
Lời giải:
Coi các chữ số của số tạo thành được xếp vào $8+k-1$ ô theo thứ tự.
B1: Xếp chữ số 0 vào 1 trong $8+k-2$ ô cuối có $8+k-2$ cách
B2: Xếp k chữ số 6 vào k trong $8+k-2$ ô còn lại có $C_{8+k-2}^k$ cách.
B3: Xếp 6 chữ số còn lại vào 6 ô còn lại có $6!$ cách
Vậy tất cả có $9.6!.C_{8+k-2}^k$ số thỏa mãn.

_______________
hxt@ Mở "rộng" này không rộng lắm nhưng đúng!

$d_{mr_1}=10$

Cho các chữ số $0,1,2,3,4,5,6,7$, có thể lập bao nhiêu chữ số có $10$ chữ số trong đó chữ số $6$ được lặp lại $3$ lần và chữ số còn lại xuất hiện đúng $1$ lần?

Toán thủ ra đề
mekjpdoj

Cách 2: Phương pháp trên là xét phần bù.. Bây giờ ta xét phương pháp trực tiếp:
Coi các chữ số xếp vào 10 ô trống theo thứ tự.
B1: Xếp số 0 vào 1 trong 9 ô cuối có $9$ cách
B2: Xếp 3 chữ số 6 vào 3 trong 9 ô còn lại có $C_{9}^3$ cách
B3: Xếp 6 chữ số còn lại vào 6 ô còn lại có $6!$ cách
Vậy tất cả có
$C_{9}^3.9.6!=544320$ cách
_______________

hxt@ Cách làm đúng!

$d_t=10$

Cho các chữ số $0,1,2,3,4,5,6,7$, có thể lập bao nhiêu chữ số có $10$ chữ số trong đó chữ số $6$ được lặp lại $3$ lần và chữ số còn lại xuất hiện đúng $1$ lần?

Toán thủ ra đề
mekjpdoj

*Ta xét số cách xếp 1 dãy 10 chữ số thoả mãn yêu cầu đầu bài tính cả số 0 ở đầu:
B1: Xếp 3 chữ số 6 vào 3 trong 10 ô có $C_{10}^3$ cách
B2: Xếp 7 chữ só còn lại vào 7 ô có $7!$ cách
Vậy có tất cả $C_{10}^3 .7!= 604800$ cách
*Xét số cách xếp mà số 0 đứng đầu trong số cách xếp dãy trên
B1: Xếp 3 chữ số 6 vào 3 trong 9 ô có $C_{9}^3$
B2: Xếp 6 chữ số còn lại vào 6 ô có $6!$ cách
Vậy có tất cả $C_{9}^3.6!=60480$
Kết luận: số các số thỏa mãn là $604800-60480=544320$ cách
ĐS: $544320$

___________
Điểm bài làm: $d=10$

$S=\left\lfloor\dfrac{52-0}{2}\right\rfloor+3\times 10+ (10+10)+10=86$

Cách 2:
Từ hệ suy ra:
$3xy-y^2=x+y$
$\Leftrightarrow (3y-1)x=y^2+y$
Với $y=\frac{1}{3}$ thì PT trên vô nghiệm.
Với $y\neq \frac{1}{3}$ thì ta có:
$\Leftrightarrow x=\frac{y^2+y}{3y-1}$
Thế vào hệ ta được:
$(\frac{y^2+y}{3y-1})+2y^2=\frac{y^2+y}{3y-1}+2y$
$\Leftrightarrow \left\{\begin{matrix} y=0\\ 19y^3-31y^2+13y-1=0 \end{matrix}\right.$
$\Leftrightarrow \begin{bmatrix} y=0\\ y=1 \\y=\frac{1}{19}(6-\sqrt{17}) \\ y=\frac{1}{19}(6+\sqrt{17}) \end{bmatrix}$
Thay vào suy ra hệ đã cho có 4 cặp nghiệm
$x=y=0$ ; $x=y=1$; $\left\{\begin{matrix} x=\frac{1}{38}(23-7\sqrt{17})\\ y=\frac{1}{19}(6-\sqrt{17}) \end{matrix}\right.$;
$\left\{\begin{matrix} x=\frac{1}{38}(23+7\sqrt{17})\\ y=\frac{1}{19}(6+\sqrt{17}) \end{matrix}\right.$

Điểm cách 10

Mở rộng: Giải hệ PT có dạng:
$\left\{\begin{matrix} ax+by=cx^2+dxy+ey^2\\ mx+ny=px^2+qxy+ry^2 \end{matrix}\right.$
TH1:
$\left\{\begin{matrix} mx+ny=0\\ px^2+qxy+ry^2=0 \end{matrix}\right.$
Thế PT đầu vào PT dưới ta giải đc nghiệm x=y=0 và nghiệm khác (nếu có)
TH2:
$\left\{\begin{matrix} mx+ny\neq 0\\ px^2+qxy+ry^2\neq 0 \end{matrix}\right.$ (1)
Ta có:
$ax+by=cx^2+dxy+ey^2$
$\Leftrightarrow (ax+by)(px^2+qxy+ry^2)=(mx+ny)(cx^2+dxy+ey^2)$
$\Leftrightarrow (ap-mc)x^3+(br-ne)y^3+(aq+bp-md-cn)x^2y+(ar+bq-nd-me)y^2x=0$ (*)
Nhận thấy từ (1) suy ra $x,y \neq 0$
Chia PT (*) cho $y^3$ và đặt $\frac{x}{y}=t$ ta được:
$\Leftrightarrow (ap-mc)t^3+(br-ne)+(aq+bp-md-cn)t^2+(ar+bq-nd-me)t=0$
Giải phương trình trên ta được nghiệm t thỏa mãn.. Khi đó:
$x=ty$ Thay vào hệ suy ra nghiệm x,y thỏa mãn!


Điểm mở rộng 10

**Với x=0 thì từ hệ suy ra y=0
Vậy $x=y=0$ là 1 nghiệm của hệ.
**Với $x,y \neq 0$ thì do $x+2y= x^2+2y^2$ nên $x+2y>0$
Do đó:
$2x+3y= x^2+3xy+y^2$
$\Leftrightarrow \left (2x+3y \right )(x^2+2y^2)= \left (x^2+3xy+y^2 \right )(x+2y)$
(lạm dụng dấu tương đương, Phương trình này là Hệ quả của hệ ban đầu)
$\Leftrightarrow x^3-2x^2y-3xy^2+4y^3=0$
$\Leftrightarrow \begin{bmatrix} x=y\\ x=\frac{1+\sqrt{17}}{2}y\\ x=\frac{1-\sqrt{17}}{2}y \end{bmatrix}$
Với x=y thay vào hệ ta được $x=y=1$ (thỏa mãn)
Với $x=\frac{\sqrt{17}-1}{2}y$ thay vào hệ suy ra $\left\{\begin{matrix} x=\frac{23+7\sqrt{17}}{38}\\ y=\frac{6+\sqrt{17}}{19} \end{matrix}\right.$ (thỏa mãn) (Nhầm lẫn đáng tiếc)
Với $x=\frac{1-\sqrt{17}}{2}y$ thay vào hệ ta được:
$\left\{\begin{matrix} x=\frac{23-7\sqrt{17}}{38}\\ y=\frac{6-\sqrt{17}}{19} \end{matrix}\right.$ (thỏa mãn)
KẾT LUẬN: Hệ đã cho có 4 cặp nghiệm
$x=y=0$; $x=y=1$; $\left\{\begin{matrix} x=\frac{23+7\sqrt{17}}{38}\\ y=\frac{6+\sqrt{17}}{19} \end{matrix}\right.$;
$\left\{\begin{matrix} x=\frac{23-7\sqrt{17}}{38}\\ y=\frac{6-\sqrt{17}}{19} \end{matrix}\right.$

Điểm: 9
S = 26 + 3x9 + 10 + 10 = 73

**Với x=0 thì từ hệ suy ra y=0
Vậy $x=y=0$ là 1 nghiệm của hệ.
**Với $x,y \neq 0$ thì do $x+2y= x^2+2y^2$ nên $x+2y>0$
Do đó:
$2x+3y= x^2+3xy+y^2$
$\Leftrightarrow \left (2x+3y \right )(x^2+2y^2)= \left (x^2+3xy+y^2 \right )(x+2y)$
$\Leftrightarrow x^3-2x^2y-3xy^2+4y^3=0$
$\Leftrightarrow \begin{bmatrix} x=y\\ x=\frac{1+\sqrt{17}}{2}y\\ x=\frac{1-\sqrt{17}}{2}y \end{bmatrix}$
Với x=y thay vào hệ ta được $x=y=1$ (thỏa mãn)
Với $x=\frac{\sqrt{17}-1}{2}y$ thay vào hệ suy ra $\left\{\begin{matrix} x=\frac{23+7\sqrt{17}}{38}\\ y=\frac{6+\sqrt{17}}{19} \end{matrix}\right.$ (thỏa mãn)
Với $x=\frac{1-\sqrt{17}}{2}y$ thay vào hệ ta được:
$\left\{\begin{matrix} x=\frac{23-7\sqrt{17}}{38}\\ y=\frac{6-\sqrt{17}}{19} \end{matrix}\right.$ (thỏa mãn)
KẾT LUẬN: Hệ đã cho có 4 cặp nghiệm
$x=y=0$; $x=y=1$; $\left\{\begin{matrix} x=\frac{23+7\sqrt{17}}{38}\\ y=\frac{6+\sqrt{17}}{19} \end{matrix}\right.$;
$\left\{\begin{matrix} x=\frac{23-7\sqrt{17}}{38}\\ y=\frac{6-\sqrt{17}}{19} \end{matrix}\right.$

Ta có:
$2013(u_{n+1}-u_n)=u_n.(u_n-1)$
$\Leftrightarrow \frac{u_n}{u_{n+1}-1}=2013(\frac{1}{u_n-1}-\frac{1}{u_{n+1}-1})$
Do đó:
$S_n=\sum_{i=1}^n\frac{u_i}{u_{i+1}-1}=2013\frac{1}{u_1-1}-2013\frac{1}{u_{n+1}-1}=2013(1-\frac{1}{u_{n+1}-1})$
Mặt khác: Xét dãy đã cho
$u_{n+1}=\frac{u_n(u_{n}-1)}{2013}+u_{n}$
Ta chứng minh dãy $u_n\geq2$ (*) với mọi $n\geq 1$
Thật vậy.. ta có (*) đúng với n=1
Giả sử (*) đúng với n=k thì $u_k\geq1$ ta cần chứng minh $u_{k+1}\geq 2$ (Sao lại 1 nhỉ)
Nhưng BDT này đúng vì $u_{k+1}=\frac{u_k(u_k-1)}{2013}+u_k> 2$
Do đó (*) đúng với mọi $n\geq 1$
Khi đó ta luôn có:
$u_{n+1}=\frac{u_n(u_n-1)}{2013}+u_n>u_n$
Do đó dãy $u_n$ là dãy tăng.. Giả sử dãy bị chặn trên. Khi đó tồn tại $\lim_{n \to +\infty }u_n=A$
Khi đó A thỏa mãn PT:
$A=\frac{A^2+2012A}{2013} \Leftrightarrow \begin{bmatrix} A=0\\ A=1 \end{bmatrix}$
Điều này vô lí do $u_n>2$ với mọi n.
Vậy $\lim_{n \to +\infty }u_{n+1}=+\infty$
Suy ra: $\lim_{n \to +\infty }\frac{1}{u_{n+1}-1}=0$
KẾT LUẬN:
$\lim_{n \to +\infty }\sum_{i=1}^n\frac{u_i}{u_{i+1}-1}=2013$

Điểm bài: 9,5
S = 26+3x9,5=54.5

Mở rộng: Khai thác biểu thức vec tơ trong tam giác:
Cho tam giác ABC bất kì.. Ta gọi D là 1 điểm bất kì thì:
$(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC})^2 \geq 0$
$\Leftrightarrow 3(DA^2+DB^2+DC^2)\geq a^2+b^2+c^2$ (*)
TH1: Cho $D\equiv O$ là tâm đường tròn ngoại tiếp tam giác ABC bán kính R thì ta có:
$a^2+b^2+c^2\leq 9R^2$
Khi đó ta có bài toán trên.
**Áp dụng BĐT $a^2+b^2+c^2\geq \frac{1}{3}(a+b+c)^2$ ta có:
$\frac{1}{3}(a+b+c)^2\leq 9R^2$
Thay $a=2RsinA, b=2RsinB, c=2RsinC$ ta có:
$sinA+sinB+sinC\leq \frac{3\sqrt{3}}{2}$

TH2: $M\equiv I$ là tâm đường tròn nội tiếp tam giác ABC bán kình r.
Gọi E là tiếp điểm của AC với đường tròn. khi đó tam giác AIE vuông tại E. Ta có:
$3(IA^2+IB^2+IC^2)\geq a^2+b^2+c^2\geq \frac{1}{3}(a+b+c)^2=\frac{4}{3}p^2$(1)
$sin\frac{A}{2}=\frac{IE}{IA}$
$\Leftrightarrow IA=\frac{r}{sin\frac{A}{2}}$
Tương tự ta có: $IB=\frac{r}{sin\frac{B}{2}}$
$IC=\frac{r}{sin\frac{C}{2}}$
Thay vào (1) ta có:
$\frac{1}{sin^2\frac{A}{2}}+\frac{1}{sin^2\frac{B}{2}}+\frac{1}{sin^2\frac{C}{2}}\geq (\frac{2p}{3r})^2$

TH3: $M\equiv H$ là trực tâm tam giác ABC nhọn. Suy ra:
$3(HA^2+HB^2+HC^2)\geq a^2+b^2+c^2\geq \frac{1}{3}(a+b+c)^2=\frac{4}{3}p^2$ (2)
Gọi A', B', C' là chân đường cao thứ tự từ đỉnh A,B,C ta có:
$HC=\frac{CA'}{sinCHA'}=\frac{ACcosC}{sinB}=2RcosC$
tương tự ta có: $HB=2RcosB, HA=2RcosA$
Thay vào (2) ta được:
$cos^2A+cos^2B+cos^2C\geq (\frac{p}{3R})^2$

Điểm mở rộng: 7
Hướng dẫn chứng minh (*): Khai triển VT và sử dụng định lí côsin trong tam giác.

Cách 2:
Ta có:
$4S=\frac{abc}{R}$ và
$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$ nên Gt tương đương với:
$sinAsinBsinC(tan\frac{A}{2}+tan\frac{B}{2}++tan\frac{C}{2})=\frac{9}{8}$
$\Leftrightarrow sinAsinB(1-cosC)+sinBsinC(1-cosA)+sinCsinA(1-cosB)=\frac{9}{8}$
$\Leftrightarrow a^2+b^2+c^2-(a-b)^2-(b-c)^2-(c-a)^2=9R^2$
$\Leftrightarrow 2ab+2bc+2ca-a^2-b^2-c^2=9R^2$ (*)
Áp dụng AM-GM ta có:
$2ab+2bc+2ca\leq 2(a^2+b^2+c^2)$ Nên
$VT(*)\leq a^2+b^2+c^2$
Gọi M là tâm đường tròn ngoại tiếp tam giác ABC ta có:
$(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC})^2\geq 0$
$\Leftrightarrow 3R^2\geq -2\overrightarrow{MA}\overrightarrow{MB}-2\overrightarrow{MA}\overrightarrow{MC}-2\overrightarrow{MB}\overrightarrow{MC}$
$\Leftrightarrow 9R^2\geq (\overrightarrow{MA}-\overrightarrow{MB})^2+(\overrightarrow{MA}-\overrightarrow{MC})^2+(\overrightarrow{MB}-\overrightarrow{MC})^2$
$\Leftrightarrow a^2+b^2+c^2\leq 9R^2$
Do đó ta có ĐPCM.
dấu bằng xảy ra khi tam giác ABC đều. các góc bằng $60^0$ và $AB=BC=CA=\frac{\sqrt{3}}{2}$

Cách 2 này giải tương đối đẹp!
Điểm: 5

Ta có: $S=\frac{abc}{4R}$
$\Leftrightarrow 4S=\frac{abc}{R}$
Mặt khác ta có:
$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$
nên $\frac{9R^2}{4S}=\frac{9}{8}\frac{1}{sinA.sinB.sinC}$
Do đó gt tương đương với:
$sinA.sinB.sinC(tan\frac{A}{2}+tan\frac{B}{2}+tan\frac{C}{2})=\frac{9}{8}$(*)
Ta chứng minh:
$tan\frac{A}{2}+tan\frac{B}{2}+tan\frac{C}{2}\leq cotA+cotB+cotC$
Thật vậy: Ta có:
$cotA+cotB=2\frac{sin(A+B)}{cos(A-B)-cos(A+B)}\geq 4\frac{sin\frac{C}{2}cos\frac{C}{2}}{1+cosC}=2tan\frac{A}{2}$
Xây dựng các BĐT tương tự cộng lại ta có ĐPCM. Áp dụng ta có:
$VT(*)\leq sinAsinBcosC+sinBsinCcosA+sinCsinAcosB$
$VT(*)\leq \frac{3}{2}-\frac{1}{2}(cos^2A+cos^2B+cos^2C)$
ta chứng minh:
$cos^2A+cos^2B+cos^2C\geq \frac{3}{4}$(1)
Giả sử A,B,C có 1 góc lớn hơn 90 độ là A thì $cos^2A\geq 0$
$B<90-C$ suy ra $cosB>sinC$ suy ra $cos^2B+ cos^2C>1$
Do đó (1) đúng:
Xét $A,B,C\leq 90^0$ giả sử C=min{A,B,C} ta có:
$cos^2A+cos^2B-2cos^2\frac{A+B}{2}=-cos(A+B)(1-cos(A-B))\geq 0$
do đó:
$VT(1)\geq 1-cosC+cos^2C\geq \frac{3}{4}$
Kết luận (1) đúng:
Do đó $VT(*)\leq VP(*)$. Dấu bằng khi tam giác ABC đều
Tóm lại:
các góc của tam giác ABC là 60 độ
$AB=AC=BC=\frac{\sqrt{3}}{2}$

Điểm: 10
S=50+3x10+5+7=92

Topic này dùng để BTC nhận đề thi từ các toán thủ thi đấu.






BTC yêu cầu các toán thủ nộp đề về Hình học không gian. Đề cần nộp cùng đáp án

Các toán thủ khi thi đấu, cứ yên tâm rằng, sau khi đánh máy là đề đã được lưu, BTC đã nhận được đề của bạn, có điều bạn không nhìn thấy được mà thôi. Bạn nên mừng vì điều này, như thế các toán thủ khác không thể biết trước đề của bạn được.

Bạn cũng nên sử dụng chức năng xem trước của diễn đàn để sửa các lỗi Latex trước khi gửi bài, vì gửi rồi sẽ không xem và sửa lại được nữa.

Đề bài:
Cho tứ diện đều S.ABC có tất cả các cạnh bằng a. Gọi G là trọng tâm tứ diện. Mặt phẳng $(P)$ là mặt phẳng qua G cắt đoạn SA, SB, SC tại thứ tự $A_1, B_1, C_1$.
Tìm mặt phẳng (P) sao cho thể tích tứ diện $S.A_1A_2A_3$ nhỏ nhất.
Bài giải:
Ta chứng minh 2 bổ đề sau:
Bổ đề 1:

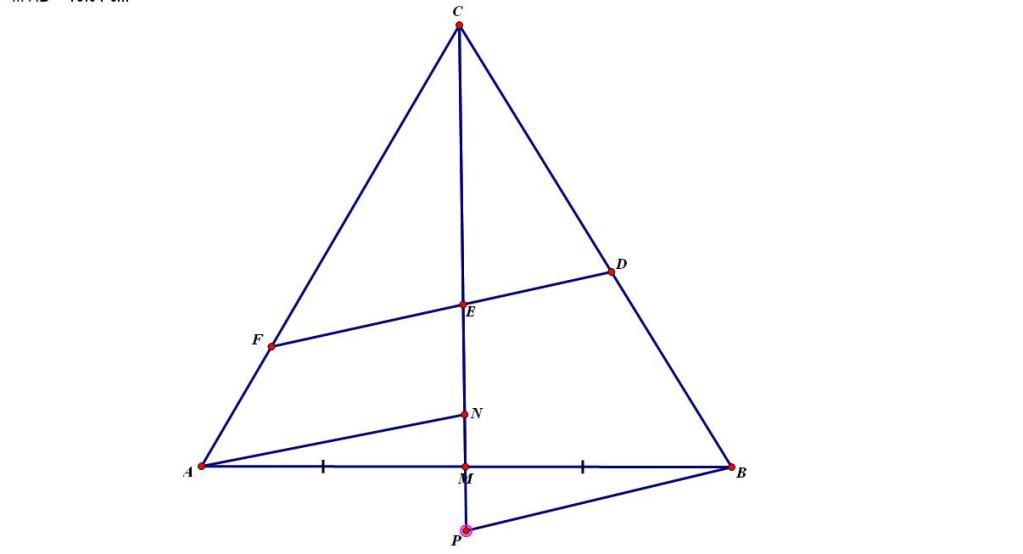
Cho tam giác ABC, M trung điểm AB, đường thẳng d là đường thẳng bất kì cắt các đoạn CB, CM, CA thứ tự tại D, E, F chứng minh:
$\frac{CA}{CF}+\frac{CB}{CD}=2\frac{CM}{CE}$
Giải:
Từ A và B kẻ các đường thẳng song song với d cắt AM thứ tự tại N và P.
$\Delta AMN= \Delta BMP$
Suy ra MN=MP
Ta có:
$\frac{CA}{CF}+\frac{CB}{CD}=\frac{CP+CN}{CE}=2\frac{CM}{CE}$
Bổ đề 2:

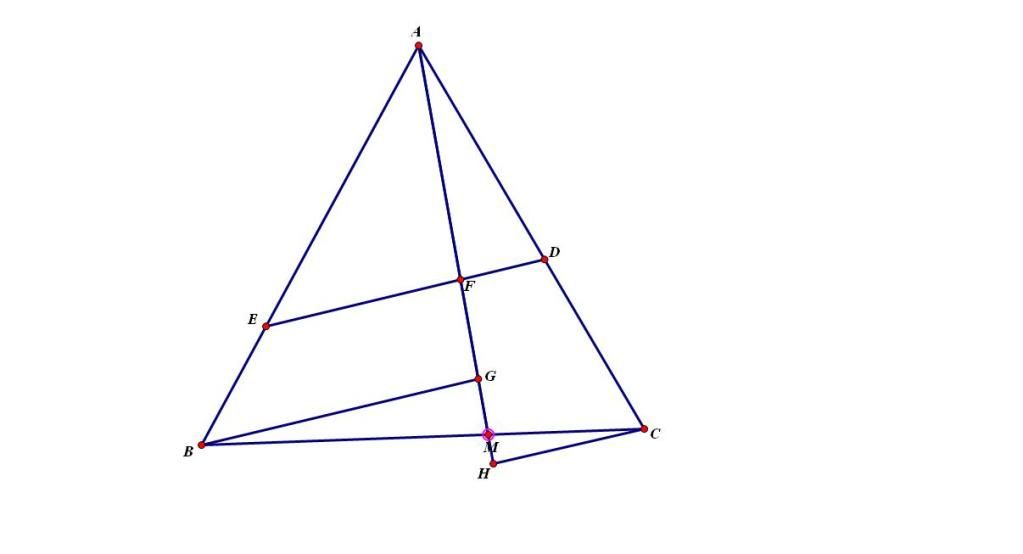
Cho tam giác ABC, M thuộc BC sao cho MB=2MC, đường thẳng d là đường thẳng bất kì cắt các đoạn AC, AB, AM thứ tự tại D, E, F chứng minh:
$\frac{AB}{AE}+2\frac{AC}{AD}=3\frac{AM}{AF}$
Chứng minh tương tự bồ để 1.
Áp dụng vào bài toán ta có:
Gọi G' là trọng tâm tam giác ABC
$\frac{SA}{SA_1}+\frac{SB}{SB_1}+\frac{SC}{SC_1}=3\frac{SG'}{SG}=4$
Áp dụng AM-GM ta có:
$4\geq 3\sqrt[3]{\frac{V_{SABC}}{V_{SA_1B_1C_1}}}$
$\Leftrightarrow V_{SA_1B_1C_1}\geq \frac{27}{64}V_{SABC}=\frac{27\sqrt2}{768}a^3$
Dấu bằng xảy ra khi mặt phẳng (P) song song với mặt phẳng (ABC)

a

Cách 2:
ĐK:$x\geq x^6$
PT đã cho tương đương:
$\frac{a^6-a^4}{\sqrt{x-a^2}}=\frac{a^6-a^4}{\sqrt{x+a^6}+\sqrt{x+a^4}}$
$\Leftrightarrow \sqrt{x-a^2}=\sqrt{x-a^6}+\sqrt{x-a^4}$
$\Leftrightarrow \sqrt{x-a^6}+\sqrt{x-a^4}-\sqrt{x-a^2}=0$ (*)
Xét $f(x)= VT (*)$
$f'(x)=\frac{1}{2\sqrt{x-a^6}}+\frac{1}{2\sqrt{x-a^4}}-\frac{1}{2\sqrt{x-a^2}}>0$
Do $\sqrt{x-a^6} < \sqrt{x-a^2}$ (Do $x\geq a^6>a^2 >1$)
Vậy hàm số đã cho có không quá 1 nghiệm trên $(a^6, +\infty)$
Xét $f(a^6)=\sqrt{a^6-a^4}-\sqrt{a^6-a^2}<0$ (a>1)
$\lim_{x \to +\infty } f(x)= \lim_{x \to +\infty }(\sqrt{x-a^6}+\sqrt{1-\frac{a^4}{x}}-\sqrt{1-\frac{a^2}{x}}) =+\infty$
Do đó PT luôn có nghiệm $x\in (a^6, +\infty)$
Kết luận: PT đã cho có đúng 1 nghiệm với mọi a>1.

Em định dùng định lý giá trị trung gian nhưng không nhắc gì đến tính liên tục của hàm số.
5 điểm

Đặt $a^2=t$ (t>1) thì phương trình đã cho trở thành:
$\sqrt{(x-t^3)(x-t)}+t^3-t^2=\sqrt{(x-t^2)(x-t)}$
Điều kiện: $x\geq t^3$
Đặt: $\sqrt{(x-t^3)(x-t)}=A$
Do 2 vế không âm bình phương 2 vế ta được:
$t^3(t-x)+t^4(t-1)^2+2t^2(t-1)A=t^2(t-x)$
$\Leftrightarrow 2A=x-t^3+t^2-t$
Vì 2 vế không âm do $x\geq t^3, t^2>t$. Bình phương ta được:
$-3x^2+2(t^3+t^2+t)x+t^6-t^4-2t^3+t^2-2t^5=0$ (*)
$\Delta' = 4(t^6-t^5-t^3+t^2)$
Áp dụng AM-GM ta có: $t^6+3t^2\geq 4t^3$ và $3t^6+t^2\geq 4t^5$ mà dấu bằng không xảy ra do $t>1$ nên
$\Delta' >0$
Khi đó (*) có 2 nghiệm phân biệt là:
$\left\{\begin{matrix} x_1=\frac{1}{3}(t^3+t^2+t-2\sqrt{\Delta'})\\ x_2= \frac{1}{3}(t^3+t^2+t+2\sqrt{\Delta'}) \end{matrix}\right.$
Ta có $x_1<t^3$ do $t^2<t^3, t<t^3, -\Delta' <0$ Do đó $x_1$ loại
Ta chứng minh $x_2 >t^3$
$\Leftrightarrow 2t^3-t^2-t< 2\sqrt{t^6-t^5-t^3+t^2}$
$\Leftrightarrow 3t^2+4t+4>0$ (Đúng)
Do đó $x_2$ thỏa mãn..
Kết luận: Với mọi a thì PT đã cho có 1 nghiệm là:

$x=\frac{1}{3}(a^6+a^4+a^2+2\sqrt{a^{12}-a^{10}-a^6+a^4})$

Điểm: 10
S = 52 + 3x10 + 5 = 87

gọi M là trung điểm AC và $ G_1 $ là trọng tâm tam giác ABC.

vì tứ diện ABCD đều nên $ SG_1$ vuông góc $ (ABC) $

G là trọng tâm tứ diện nên $ G \in SG_1 $ và $ SG=\frac{2}{3}SG_1 $

ta có: $ SM=MB=\frac{a\sqrt{3}}{2} $ (do là trung tuyến của tam giác đều)

$ \Rightarrow MG_1=\frac{1}{3}MB=\frac{a}{2\sqrt{3}} $

tam giác $SG_1M $ vuông tại $ G_1 $

$ \Rightarrow SG_1=\sqrt{SM^2-MG_1^2}=a\sqrt{\frac{2}{3}} $

$ \Rightarrow V_{S.ABC}=\frac{1}{3}.SG_1.S_{ABC}=\frac{a^3\sqrt{2}}{12} $

lấy 2 điểm $ A_1; B_1 $ lần lượt thuộc SA;SB

vì $ B_1G $ và SM cùng thuộc mặt phẳng (SMB) nên $B_1G \cap SM= N$

$ A_1N $ và SC cùng thuộc $ mp(SAC) $ nên $ A_1N \cap SC=C_1 $

$ \Rightarrow (P) \equiv (A_1B_1C_1) $

đặt $ AA_1=x, BB_1=y, CC_1=z $

áp dụng công thức về tỉ số thể tích cho 2 khối tứ diện $ S.A_1B_1C_1 $ và $ S.ABC $ ta có:

$ \frac{V_{S.A_1B_1C_1}}{V_{S.ABC}}=\frac{SA_1.SB_1.SC_1}{SA.SB.SC}=\frac{xyz}{a^3} $

$ \Rightarrow V_{S.A_1B_1C_1}=\frac{xyz\sqrt{2}}{12} $ (1)

mặt khác, áp dụng công thức tỉ số thể tích cho 2 khối tứ diện $ S.A_1B_1.G $ và $ S.ABG_1 $ ta có:

$ \frac{V_{S.A_1B_1G}}{V_{S.ABG_1}}=\frac{SA_1.SB_1.SG}{SA.SB.SG_1}$

$ \Rightarrow V_{S.A_1B_1G}=\frac{2xy}{3a^2}.V_{S.ABG_1} $

chứng minh tương tự ta có:

$ V_{S.B_1C_1G}=\frac{2yz}{3a^2}.V_{S.BCG_1} $

$ V_{S.C_1A_1G}=\frac{2zx}{3a^2}.V_{S.CAG_1} $

mà $ V_{S.ABG_1}=V_{S.BCG_1}=V_{S.CAG_1}=\frac{V_{S.ABC}}{3} $

$ \Rightarrow V_{S.A_1B_1G}+V_{S.B_1C_1G}+ V_{S.C_1A_1G}=\frac{2zx}{3a^2}.V_{S.ABC} $

hay $ V_{S.A_1B_1C_1}=\frac{a\sqrt{2}}{18}(xy+yz+zx) $ (2)

từ (1) và (2) suy ra:

$ 3xyz=2a(xy+yz+zx) $

áp dụng bất đẳng thức AM-GM ta có:

$ 3xyz=2a(xy+yz+zx) \geq 6a\sqrt[3]{x^2y^2z^2}$

$ \Rightarrow xyz \geq \frac{8a^3}{27} $

$ \Rightarrow V_{S.A_1B_1C_1} \geq \frac{2a^3\sqrt{2}}{81}$

dấu bằng xảy ra khi $ AA_1= BB_1=CC_1=\frac{2}{3} $ hay (P) là mặt phẳng qua G và song song với BC.

10 điểm

Cách làm đúng rồi nhwung mà số má sai hết rồi .. Tỉ số $\frac{SG}{SG_1}=\frac{3}{4}$..

Sao trận này toán thủ ra đề BoFake không được điểm nhỉ??