Các bạn có thể xem thêm các ứng dụng và mở rộng hai bài hình học ở đây
Có 489 mục bởi quanghung86 (Tìm giới hạn từ 07-06-2020)
 Đã gửi bởi
quanghung86
on 21-08-2015 - 18:14
trong
Thi HSG Quốc gia và Quốc tế
Đã gửi bởi
quanghung86
on 21-08-2015 - 18:14
trong
Thi HSG Quốc gia và Quốc tế
Các bạn có thể xem thêm các ứng dụng và mở rộng hai bài hình học ở đây
 Đã gửi bởi
quanghung86
on 26-08-2015 - 22:50
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Đã gửi bởi
quanghung86
on 26-08-2015 - 22:50
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Đúng là chỗ đó thầy làm hơi tắt quá. Giải thích kỹ hơn như sau $PT//OM$ hơn nữa $OP//TM$ vì cùng vuông góc với dây cung chung của $(AEF)$ và $(O)$, chú ý dây cung chung này chính là phân giác ngoài góc $A$. Từ đó $POMT$ là hbh nên $POJM$ cũng là hbh hay $N$ là trung điểm $OM$.
 Đã gửi bởi
quanghung86
on 29-08-2015 - 12:36
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Đã gửi bởi
quanghung86
on 29-08-2015 - 12:36
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Cám ơn Toàn về đóng góp những ý tưởng hay từ cấu hình này và lời giải hay, lời giải của thầy hơi mẹo mực một chút, hãy đón đọc vào thứ 2 nhé ![]() , bài này là một bài thầy thích về tính đơn giản của đề bài và tính không đơn giản của lời giải
, bài này là một bài thầy thích về tính đơn giản của đề bài và tính không đơn giản của lời giải ![]()
 Đã gửi bởi
quanghung86
on 29-08-2015 - 12:39
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Đã gửi bởi
quanghung86
on 29-08-2015 - 12:39
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Spriral similarity hiểu theo nghĩa tiếng Việc là một phép "vị tự quay", ở đây trong thuật ngữ tiếng Việt, phép "vị tự quay" là tích của phép quay và phép vị tự với tâm quay và tâm vị tự trùng nhau, đương nhiên nó là một phép đồng dạng đặc biệt.
 Đã gửi bởi
quanghung86
on 29-08-2015 - 20:46
trong
Hình học
Đã gửi bởi
quanghung86
on 29-08-2015 - 20:46
trong
Hình học
Bài này là hệ quả của bài toán con bướm, bản thân phát biểu này cũng có lâu rồi mà, đây là một ứng dụng đẹp của nó
 Đã gửi bởi
quanghung86
on 07-09-2015 - 19:52
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Đã gửi bởi
quanghung86
on 07-09-2015 - 19:52
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Cám ơn Toàn đã dẫn lại link, đúng là một lời giải hay lâu rồi thầy cũng quên mất ![]() , qua link đó ta cũng thấy bài toán này và bài chọn đội tuyển Đài Loan 2014 có liên quan mật thiết với nhau. Xin được trích dẫn lại bài chọn đội Đài Loan 2014 như sau
, qua link đó ta cũng thấy bài toán này và bài chọn đội tuyển Đài Loan 2014 có liên quan mật thiết với nhau. Xin được trích dẫn lại bài chọn đội Đài Loan 2014 như sau
Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ và tâm ngoại tiếp $O$. $OI$ cắt tiếp tuyến của $(I)$ song song với $BC$ tại $M$. Cũng trên tiếp tuyến này lấy điểm $N$ sao cho $IN\perp IO$. Chứng minh rằng bốn điểm $A,M,O,N$ cùng thuộc một đường tròn.
Đây là một bài toán hay có nhiều nghĩa và có nhiều phát triển rất thú vị.
 Đã gửi bởi
quanghung86
on 08-09-2015 - 20:14
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Đã gửi bởi
quanghung86
on 08-09-2015 - 20:14
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Đáp án của thầy có dùng tính chất hàng điều hòa.
 Đã gửi bởi
quanghung86
on 11-09-2015 - 19:37
trong
Hình học
Đã gửi bởi
quanghung86
on 11-09-2015 - 19:37
trong
Hình học
Cám ơn bạn huypham2811 cho một lời giải khá ngắn gọn, bài này mình đề nghị trên THTT trước đây, sau đây là đề bài gốc và đáp án
Cho tam giác $ABC$. $E,F$ lần lượt thuộc đoạn $CA,AB$ sao cho $EF$ song song $BC$. Trung trực $BC$ cắt $AC$ tại $M$. Trung trực $EF$ cắt $AB$ tại $N$. Đường tròn ngoại tiếp tam giác $BCM$ cắt $CF$ tại $P$ khác $C$. Đường tròn ngoại tiếp tam giác $EFN$ cắt $CF$ tại $Q$ khác $F$. Chứng minh rằng trung trực của $PQ$ đi qua trung điểm của $MN$.
Gọi $H,G$ là hình chiếu của $M,N$ lên $CF$. Gọi $K,L$ lần lượt là hình chiếu của $E$ lên $BC$ và $B$ lên $EF$. Gọi $I,J$ là trung điểm của $BC,EF$. Ta sẽ chứng minh trung trực của $PQ$ đi qua trung điểm $MN$ bằng cách chỉ ra $PH=QG$, thật vậy
Ta dễ có $\angle MPH=\angle MBC=\angle MCB$. Nên các tam giác giác vuông $\triangle MPH\sim\triangle ECK$. Vậy ta có $PH=HM\dfrac{CK}{EK}=HM\dfrac{CI}{MI}\quad (1)$.
Tương tự $\triangle NQG\sim\triangle BFL$ suy ra $QG=NG\dfrac{FL}{BL}=NG\dfrac{FJ}{NJ}\quad (2)$.
Từ (1) và (2) ta có $PH=QG$ khi và chỉ khi $HM\dfrac{CI}{MI}=NG\dfrac{FJ}{NJ}$ tương đương $\dfrac{HM}{NG}=\dfrac{MI.FJ}{CI.NJ}=\dfrac{MI}{NJ}.\dfrac{EF}{BC}\quad (3)$.
Ta lại có $MH.FC=2S_{MFC}=2\dfrac{S_{MFC}}{S_{EFC}}.S_{EFC}=2\dfrac{MC}{CE}.\dfrac{1}{2}EK.EF=\dfrac{MC.EK.EF}{EC}\quad (4)$.
$NG.FC=2S_{SFC}=2\dfrac{S_{NFC}}{S_{BFC}}.S_{BFC}=2\dfrac{NF}{FB}.\dfrac{1}{2}BL.BC=\dfrac{NF.BL.BC}{FB}\quad (5)$.
Từ (4) và (5) ta suy ra $\dfrac{MH}{NG}=\dfrac{MC.EK.EF.FB}{NF.BL.BC.EC}=\dfrac{MC.EF.FB}{NF.BC.EC}=\dfrac{FB}{NF}.\dfrac{MC}{EC}.\dfrac{EF}{BC}=\dfrac{BL}{NJ}.\dfrac{MI}{EK}.\dfrac{EF}{BC}=\dfrac{MI}{NJ}.\dfrac{EF}{BC}\quad (6)$.
Từ (6) suy ra (3) đúng. Vậy $PH=QG$. Từ đó trung trực $PQ$ đi qua trung điểm $MN$. Ta có điều phải chứng minh.
 Đã gửi bởi
quanghung86
on 14-09-2015 - 02:29
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 14-09-2015 - 02:29
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Bài hình này chính xác là một mở rộng của bài toán thi vòng 1 chuyên KHTN.
Từ bài toán thi vòng 1 đó tới bài toán TST của HSGS chỉ khác nhau một giả thiết nhỏ, nhưng lời giải khác nhau khá xa, có lẽ đó là điều thú vị của bài toán này, khi đợt thi kết thúc, tôi sẽ giới thiệu đáp án đầy đủ.
 Đã gửi bởi
quanghung86
on 16-09-2015 - 09:58
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 16-09-2015 - 09:58
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Lời giải của Toàn rất thú vị, hãy tham khảo thêm các cách chứng minh khác và mở rộng ở đây
 Đã gửi bởi
quanghung86
on 18-09-2015 - 19:22
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Đã gửi bởi
quanghung86
on 18-09-2015 - 19:22
trong
Chuyên mục Mỗi tuần một bài toán Hình học
Uầy chị Chi Lan giải nhanh quá ![]()
![]()
![]()
 Đã gửi bởi
quanghung86
on 18-09-2015 - 20:11
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Đã gửi bởi
quanghung86
on 18-09-2015 - 20:11
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Cám ơn em, tài liệu rất hay, các đề Hàn Quốc có nhiều đề chất lượng cao nhưng được biến đến rải rác quá không hệ thống, ngay cả trên AoPS cũng vậy, giờ tập hợp được thế này thì tốt quá rồi ![]()
 Đã gửi bởi
quanghung86
on 19-09-2015 - 08:57
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Đã gửi bởi
quanghung86
on 19-09-2015 - 08:57
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Bài viết đã được update ![]() !
!
 Đã gửi bởi
quanghung86
on 19-09-2015 - 09:21
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 19-09-2015 - 09:21
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Một số gợi ý cho câu b) bài hình
- Tích của hai phép đối xứng trục mà hai trục vuông góc là đối xứng tâm
- Có một bài toán quan trọng sau được dùng làm bổ đề
Cho tam giác $ABC$, trực tâm $H$, đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ lần lượt tại $D,E,F$. $K$ là hình chiếu của $D$ lên $EF$. Chứng minh rằng $KD$ là phân giác $\angle IKH$.
 Đã gửi bởi
quanghung86
on 19-09-2015 - 10:17
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 19-09-2015 - 10:17
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Topic này mở ra để xin giới thiệu về các kỳ thi HSG toán của trường THPT chuyên KHTN. Trường THPT chuyên KHTN là ngôi trường cấp 3 giàu truyền thống nhất cả nước nên các kỳ thi HSG toán của trường được đặc biệt quan tâm và chú ý. Các đề thi trong các kỳ thi này cũng rất chất lượng tiệm cận chuẩn quốc tế.
Đặc điểm của kỳ thi HSG lớp 10 là để chọn đội dự tuyển nên kiến thức nằm chủ yếu trong phần THCS nhưng cấp độ đề thi cao. Các cuộc thi HSG 10 sau kỳ chọn dự tuyển là chủ yếu để kiểm tra mức học của đội dự tuyển sau khi kết thúc chuyên đề nên đề thi rất đa dạng và phong phú, ứng với mỗi chuyên đề đội dự tuyển được học. Số lượng kỳ thi HSG lớp 10 trong một năm học là không hạn chế.
Đặc điểm của kỳ thi HSG lớp 11, 12 là để chọn học sinh lớp 11,12 đi thi quốc gia. Kỳ thi này thi theo vòng, mỗi vòng có 2 ngày thi giống như thi IMO. Các năm trước năm 2012 thì kỳ thi vẫn diễn ra theo 3 vòng truyền thống, từ năm 2012 trở lại kỳ thi tổ chức trong 2 vòng thi. Đề thi HSG lớp 11,12 thường có tính phân loại rất cao và tiếp cận các kỳ thi quốc gia, quốc tế, lượng kiến thức sử dụng là không hạn chế.
Từ năm 2014 trường THPT chuyên KHTN tổ chức kỳ thi Olympic chuyên KHTN với sự tham gia của rất nhiều trường THPT chuyên trên cả nước. Đây là kỳ thi chất lượng và uy tín, đề thi tiếp cận chuẩn đề thi IMO.
Từ khi mạng internet phát triển, nhiều đề thi đã được đưa lên mạng, topic này xin dẫn lại link đến các đề thi đó từ http://diendantoanhoc.net, chúng tôi cố gắng bắt đầu từ năm 2009 cho đến nay nhưng vì đề không phải lúc nào cũng được post lên mạng nên không thể tập hợp được đầy đủ ngay, đề thi mới và các đường link mới sẽ được update liên tục.
Trần Quang Hùng.
Đề HSG lớp 10
Năm 2011
Năm 2012
HSG KHTN lớp 10 năm 2012
Năm 2013
Năm 2014
Năm 2015
HSG KHTN lớp 10 năm 2015 đợt 2
HSG KHTN lớp 10 năm 2015 đợt 3
Năm 2016
HSG KHTN lớp 10 năm 2016 khóa 51
Đề HSG lớp 11,12
Năm 2009
HSG KHTN lớp 11,12 năm 2009 vòng 1: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2009 vòng 2: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2009 vòng 3: Ngày 1, Ngày 2
Năm 2010
HSG KHTN lớp 11,12 năm 2010 vòng 1: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2010 vòng 2: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2010 vòng 3: Ngày 1, Ngày 2
Năm 2011
HSG KHTN lớp 11,12 năm 2011 vòng 1: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2011 vòng 2: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2011 vòng 3: Ngày 1, Ngày 2
Năm 2012
HSG KHTN lớp 11,12 năm 2011 vòng 1: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2012 vòng 2: Ngày 1, Ngày 2
Năm 2013
HSG KHTN lớp 11,12 năm 2013 vòng 1: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2013 vòng 2: Ngày 1, Ngày 2
Năm 2014
HSG KHTN lớp 11,12 năm 2014 vòng 1: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2014 vòng 2: Ngày 1, Ngày 2
Năm 2015
HSG KHTN lớp 11,12 năm 2015 vòng 1: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2015 vòng 2: Ngày 1, Ngày 2
Năm 2016
HSG KHTN lớp 11,12 năm 2016 vòng 1: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2016 vòng 2: Ngày 1, Ngày 2
Năm 2017
HSG KHTN lớp 11,12 năm 2017 vòng 1: Ngày 1, Ngày 2
HSG KHTN lớp 11,12 năm 2017 vòng 2: Ngày 1, Ngày 2
Olympic chuyên KHTN (chi tiết về kỳ thi xem tại đây)
Olympic chuyên KHTN năm 2014 Ngày 1+Ngày 2
Olympic chuyên KHTN năm 2015 Ngày 1+Ngày 2
Olympic chuyên KHTN năm 2016 Ngày 1+Ngày 2
 Đã gửi bởi
quanghung86
on 19-09-2015 - 18:34
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 19-09-2015 - 18:34
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
ĐỀ THI HỌC SINH GIỎI TOÁN LỚP 11+12 VÒNG 1 NĂM HỌC 2010
Ngày thi thứ nhất
Câu 1. Tìm các cặp nguyên dương $(x,y)$ thỏa mãn phương trình
$$(x+1)^4+(x+2)^4+....+(x+2011)^4=4^y.$$
Câu 2. Cho $a_0,a_1>0$. Xét dãy {$a_n$} thỏa $a_{n+1}=\dfrac{2}{a_n+a_{n-1}}$. Chứng minh dãy có giới hạn hữu hạn khi n tiến tới vô cùng và tìm giới hạn đó.
Câu 3. Tam giác$ ABC$ nhọn,$D$ nằm trong tam giác thỏa mãn $\widehat{ADB}=60^\circ +\widehat{ACB} $ và $DA.BC=DB.AC$. Chứng minh rằng $DC.AB=AD.BC$
Câu 4. Tìm số hoán vị ${a_1,a_2,...,a_n} $của {1,2,3,...,n} ($n\geq 2)$ thỏa mãn cả hai điều kiện sau
1) $a_i \neq $ $i$ với mọi$ i=1,2,..,n$
2) $a_{i+1}-a_i \leq 1$ với mọi$ i=1,2,..,n-1$
ĐỀ THI HỌC SINH GIỎI TOÁN LỚP 11+12 VÒNG 1 NĂM HỌC 2010
Ngày thi thứ hai
Câu 1. Giải hệ sau $\left\{\begin{matrix}x+3y=x^3-12\\-y+4z=y^3-6\\ 9z+2x=z^3+32\end{matrix}\right.$
Câu 2. Cho$ a$ là số nguyên dương có ít nhất một ước nguyên tố khác $2$ và $5$.CMR với $k$ là số dương bất kì, luôn tồn tại vô hạn $n$ thỏa mãn $S(n)>k.S(an)$ Trong đó $S(x)$ là hàm tổng các chữ số của $x$ nguyên dương.
Câu 3. Kí hiệu$ I$ là tâm nội tiếp$ ABC$. Đường thẳng vuông góc với $IA $ tại $A$ cắt $BI,CI$ tại $K,M$. Gọi $B',C'$ là giao điểm của $2$ cặp $(BI,AC),(CI,AB)$. Đường thẳng $B'C'$ cắt $(O)=(ABC)$ tại $N,E$. Chứng minh rằng bốn điểm $M,N,E,K$ thuôc cùng một đường tròn.
Câu 4. Một trò chơi được chơi bởi $2$ người rất giỏi bằng cách bẻ $1$ thanh gỗ có độ dài nguyên thành $2$ thanh gỗ có độ dài nguyên khác nhau. Trò chơi bất đầu với thanh có $\l =2010$. Hai bạn $A,B$ chơi lần lượt, $A$ đi trước. Trò chơi kết thúc nếu thanh gỗ có độ dài $1$ or $2$ ($k$ thể bẻ tiếp để thỏa mãn đề được nữa). Nếu kết thúc mà số thanh độ dài $1$ lớn hơn số thanh độ dài $2$ thì người đi bước cuối thắng, nếu ngược lại nhỏ hơn thì người đi bước cuối thua, nếu bằng thì hòa. Hãy xác định kết quả trò chơi ?
 Đã gửi bởi
quanghung86
on 19-09-2015 - 18:39
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 19-09-2015 - 18:39
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
ĐỀ THI HỌC SINH GIỎI TOÁN LỚP 11+12 VÒNG 2 NĂM HỌC 2010
Ngày thi thứ nhất
Câu 1. Cho trước số nguyên dương lẻ $n$. Trong tất cả các cặp $(a,b)$nguyên dương thỏa mãn $\left\{\begin{matrix} a+nb\ \vdots\ n+2 \\ a+(n+2)b\ \vdots\ n \end{matrix}\right.$ Tìm giá trị nhỏ nhất của $P=a+b$.
Câu 2. Tìm tất cả các số nguyên dương $n$ sao cho tồn tại hàm $f: \mathbb{R}_+ \to \mathbb{R}_+$ thỏa mãn $f(x+y)\ge y \cdot f_n(x) \,\, \forall x,y >0$ và $f_n(x)$ là hàm hợp bậc $n$.
Câu 3. Cho tứ giác toàn phần $ABCDEF$, trong đó tứ giác $ABCD$ có đường tròn nội tiếp tâm $I$. Gọi $A_1, B_1, C_1, D_1$ là tiếp điểm của $(I)$ với các cạnh $AB, BC, CD, DA$. Gọi $M$ là hình chiếu của $I$ lên $EF$. Hình chiếu của $M$ lên các đường thẳng $A_1B_1,$ $B_1C_1,$ $C_1D_1,$ $D_1A_1$ là $M_1,M_2,M_3,M_4$. Chứng minh rằng $M_1,M_2,M_3,M_4$ thẳng hàng.
Câu 4. Cho $n$ là số nguyên dương. Xét 1 bảng ô vuông kích thước $n\times n$ được chia thành $n^2$ ô vuông con. Ban đầu tất cả ô vuông con đều trống. Mỗi bước ta chọn ra $n$ ô vuông con khác hàng và khác cột đôi một khác nhau, sau đó thêm vào chúng một ngôi sao. Chứng minh rằng từ một bảng $n\times n$ trống, sau 2010 bước thực hiện, ta thu được bảng có tổng sô ngôi sao trên mỗi hàng, mỗi cột đều bằng 2010.
ĐỀ THI HỌC SINH GIỎI TOÁN LỚP 11+12 VÒNG 2 NĂM HỌC 2010
Ngày thi thứ hai
Câu 1. Tìm tất cả các cặp $(m,n)$ cùng tính chãn lẻ sao cho $2(m^2+n^2)\vdots m^2-n^2-4$.
Câu 2. Giả sử đa thức $P(x)\in \mathbb{R}[x]$ thỏa mãn $P(2x^3+x)=P(x)\cdot P(2x^2)$. Chứng minh rằng $P(x^2)\cdot P(y^2)\ge P(xy)$.
Câu 3. Cho 2 điểm $A,B$ cố định và $(O)$ thay đổi. $a,b$ là đường đối cực của $A,B$ đối với $(O)$ thỏa mãn $\dfrac{d(A,b)}{d(B,a)}=2$. Xác định vị trí của $O$ để $S_{OAB}$ lớn nhất.
Câu 4. Một $4k$-giác đều chia thành các hình bình hành không cắt nhau (có thể chung một phần cạnh)
1) Chứng minh rằng trong số các hình bình hành đó có ít nhất $k$ hình chữ nhật.
2) Giả sử cạnh đa giác đều là 1. Tính tổng diện tích tất cả các hình chữ nhật trong cách chia trên.
 Đã gửi bởi
quanghung86
on 19-09-2015 - 18:50
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 19-09-2015 - 18:50
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Ngày 2
Câu 1. Cho dãy số $a_n$ được xác định như sau
$a_1=\dfrac{5}{2}$ và $a_{n+1}=a_n^3-3a_n^2+6a_n-3$
với mọi $n\geq 1$. Tìm số nguyên dương n nhỏ nhất sao cho $[a_n]+1$ chia hết cho $3^{2011}$
Câu 2. Ký hiệu $S=\left \{ x\in R,x>1 \right \}$. Tìm tất cả các hàm số $f:\mathbb S\to\mathbb R$ thỏa mãn $f(x^5+y^5)=x^4f(x)+y^4f(y)$
Câu 3. Cho tứ giác lồi $ABCD$ không là hình thang, hai đường chéo không vuông góc nội tiếp $(O)$. $P$ là điểm trên cung $AB$ nhỏ không chứa $C,D$. $PD$ cắt $AC$ tại $M$, $PC$ cắt $BD$ tại $N$. $Q$ là giao điểm khác $P$ của $(APM)$ và $(BPN)$.
1) Chứng minh $PQ$ luôn đi qua điểm $T$ cố định
2) Gọi $AC$ giao $BD$ tại $E$, $I$ là trung điểm $CD$. Chứng minh rằng $E,I,T$ thẳng hàng.
Câu 4. Trên bàn cờ kích thức $p\times p$ (p là số nguyên tố có dạng $4k+3$), ô ở hàng thứ $i$,cột thứ $j$ kí hiệu là $(i,j)$. Lúc đầu đặt một quân cờ ở (1,1). Biết rằng có thể di chuyển quân cờ theo quy tắc: ở mỗi bước quân cờ đi từ ô $(i_1,j_1)$ sang ô $(i_2,j_2)$ thỏa mãn $(i_1-i_2)^2+(j_1-j_2)^2\equiv 1 \pmod p$. Tìm số $n$ nhỏ nhất sao cho quân cờ có thể đi từ (1,1) đến bất kì ô nào khác sau không quá $n$ bước.
 Đã gửi bởi
quanghung86
on 19-09-2015 - 18:53
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 19-09-2015 - 18:53
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Ngày 2
Câu 1. Cho $k$ là số thực dương thỏa mãn $[k.n^2]$ là số chính phương với mọi số nguyên dương $n$.Chứng minh rằng $k$ là số chính phương.
Câu 2. Cho $ f :\mathbb R\to \mathbb R$ là hàm bị chặn thỏa mãn $f^2(x+y)\geq f^2(x)+2f(xy)+f^2(y)$ với mọi $x,y\in\mathbb R.$ Tìm tất cả các giá trị có thể có của $f(x)$.
Câu 3. Cho tứ giác $ABCD$, $AD$ giao $BC$ tại $E$. $I$ là trung điểm $CD$. $EI$ cắt $(EAB)$ tại $M$. $F$ là giao điểm hai đường chéo $AC$ và $BD$. $N$ là giao của $EF$ và $(EAB)$. Chứng minh $C,D,M,N$ đồng viên.
Câu 4. Cho $k,n\in\mathbb Z+$. Giả sử G là một đồ thị vô hướng có n đỉnh thỏa mãn: Nếu ta bỏ đi một đỉnh bất kì và các cạnh nối với nó thì độ thị còn lại liên thông. Hai người A,B chơi một trò chơi như sau: A chọn hai đỉnh p,q nào đó của G, B định hướng cho nhiều nhất k cạnh của G; sau đó A định hướng cho tất cả các cạnh còn lại và chọn một cạnh r đã định hướng. Nếu trong đồ thị vừa định hướng có một con đường đi từ p đến q mà đi qua r thfi B thắng,và ngược lại A thắng. Chứng minh rằng
i) Nếu $k=2n-4$ thì tồn tại đồ thị G mà A có chiên thuật thắng
ii) Nếu $k=2n-3$ thì B có chiến thuật thắng.
 Đã gửi bởi
quanghung86
on 19-09-2015 - 18:56
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 19-09-2015 - 18:56
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Vòng 3 năm 2009 Ngày 2
Câu 1. Với mỗi $n$ lớn hơn hoặc bằng $2$ , xét ước chung lớn nhất của tất cả các cặp cặp có thể của hai số khác nhau từ $1$ đến $n$. Gọi $A(n), B(n)$ lần lượt là trung bình cộng và trung bình nhân của các ước số đó.
1) chứng minh rằng $A(n)< \ln n+1$ và tính $\lim A(n)$
2) Chứng minh rằng $B(n) < e^3$.
Câu 2. Chứng minh rằng với mọi dãy $a_1,a_2,...a_n$ ($n$ nguyên dương) ta luôn chọn được số tự nhiên $ k \le n$ sao cho $(a_1+a_2+...+a_k)-(a_{k+1}+...+a_n)| \le \max\{|a_1|,|a_2|...|a_n|\}$.
Câu 3. Hai đường tròn tâm $O$ và $O'$ tiếp xúc trong với nhau tại $A$ ($(O')$ nằm trong $(O)$). Giả sử dây cung $BC$ của đường tròn $(O)$ cắt $(O')$ tại $M,N$ sao cho $MB=MC$ và $N$ trên đoạn $MB$. $AN$ cắt $(O)$ lần hai tại $E$. trên cung $BEC$ ta lấy điểm $K$ sao cho $OK$ đi qua $M$. Dây $AK$ cắt $BC$ tại $F$. Chứng minh rằng bốn điểm $E,F,M,K$ nằm trên một đường tròn.
Câu 4. Giả sử ta có thể chọn được n số phân biệt từ tập {1,2,3...2n-1} sao cho các số được chọn không có hai số nào chia hết cho nhau. Chứng minh rằng không có số nào trong các số trên nhỏ hơn $2^k$, k là số xác định bởi điều kiện $3^k < 2n<3^{k+1}$
 Đã gửi bởi
quanghung86
on 19-09-2015 - 23:07
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 19-09-2015 - 23:07
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
ĐỀ THI HỌC SINH GIỎI TOÁN LỚP 11+12 VÒNG 3 NĂM HỌC 2010
Ngày thi thứ nhất
Câu 1. Tìm tất cả các đa thức $P(x)\in\mathbb{R\text{[x]}}$ thỏa mãn $P(x-y)+P(y-z)+P(z-x)=3P(x)+3P(y)+3P(z)$ với $\forall x,y,z\in\mathbb{R}$ mà $x+y+z=0$.
Câu 2. Cho dãy số${a_{n}}$ xác định như sau $a_{1}=0$ và $a_{n+1}=\frac{{(4n+2).n^{3}}}{(n+1)^{4}}a_{n}+\frac{3n+1}{(n+1)^{4}}\ \forall n=1,2,3,...$. Chứng minh rằng tồn tại vố số số nguyên dương $n$ thỏa mãn $a_{n}$ là số nguyên dương.
Câu 3. Cho lục giác $AMBDNC$ thỏa mãn $AC=BD$ và $MN$ là đường kính đường tròn ngoại tiếp $MC$ cắt$ AD,AN$ tại $F,P$ và $MD$ cắt $BC,BN$ taị $E,Q$. Chứng minh rằng $\frac{\overline{CP}}{\overline{CM}}+ \frac{\overline{FP}}{\overline{FM}}+ \frac{\overline{DQ}}{\overline{DM}}+ \frac{\overline{EQ}}{\overline{EM}} $
là hằng số.
Câu 4. Trên vòng tròn có một số điểm được tô bởi một trong 2 màu xanh hoặc đỏ.Mỗi bước thực hiên cho phép xó đi hoặc thêm vào một điểm tô màu đỏ (điểm thêm vào nằm trên vòng tròn và không trùng các điểm cho trước),đồng thời hai điểm kề với nó (trước khi xóa hoặc sau khi thêm) được đổi màu: xanh $\rightarrow$ đỏ và ngược lại. Giả sử ban đầu có đúng hai điểm màu đỏ và sau mỗi bước thực hiện ta không được để lại ít hơn 2 điểm. Hỏi sau số hữu hạn bước có thể thu được vòng tròn có:
$i)$ 2009 điểm màu xanh và 1 điểm màu đỏ
$ii)$ 2010 điểm màu xanh và 1 điểm màu đỏ
$iii)$ 2010 điểm màu xanh
ĐỀ THI HỌC SINH GIỎI TOÁN LỚP 11+12 VÒNG 3 NĂM HỌC 2010
Ngày thi thứ hai
Câu 1. Cho dãy số $a_{n}$ thỏa mãn $0<a_{n+1}-a_{n}\leq2010$. Chứng minh rằng tồn tại vô số cặp số nguyên dương $(p,q)$ thỏa mãn $p<q$ thì $a_{p}|a_{q}$
Câu 2. Tìm $x,y,z$ thỏa mãn hệ $\left\{\begin{matrix}
&2z(x+y)+1=x^{2}-y^{2} \\
& y^{2}+z^{2}=1+2xy+2xz-2yz \\
& y(3x^{2}-1)=-2x(x^{2}+1)
\end{matrix}\right.$
Câu 3. Hai đường tròn $(O_{1})$ và $(O_{2})$ cắt nhau tại $A,B$ và $I$ là trung điểm $O_{1}O_{2}$. Gọi $C$ là đối xứng của $B$ qua $I$. Một đường tròn $(O)$ đi qua $A,C$ cắt hai đường tròn đã cho tại $M,N$ khác $A$. Chứng minh rằng $CM=CN$.
Câu 4. Gọi $\mathbb{N}$ là tập hợp các số tự nhiên. Tìm tất cả các hàm số $f:\mathbb{N\times N}\rightarrow\mathbb{N}$ thỏa mãn
i) $f(a,b)=f(b,a)$
ii) $f(b,f(a,b))=a$
iii) Nếu $f(a,b)>c$ thì $f(b,c)<a$
 Đã gửi bởi
quanghung86
on 19-09-2015 - 23:22
trong
Hình học
Đã gửi bởi
quanghung86
on 19-09-2015 - 23:22
trong
Hình học
Kiểm tra đội dự tuyển 10 chuyên KHTN tháng 4 năm 2015
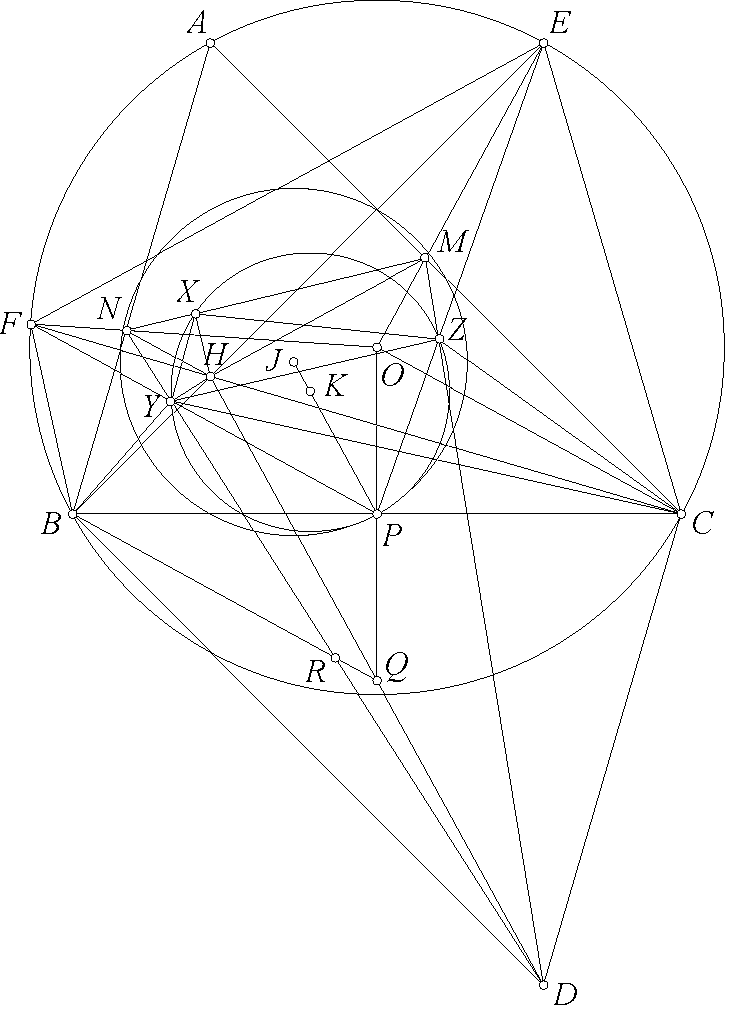
Bài 1. Cho tam giác $ABC$ nội tiếp $(O)$, trực tâm $H$. $E,F$ đối xứng $H$ qua $CA,AB$. $OE,OF$ lần lượt cắt $CA,AB$ tại $M,N$. Dựng hình bình hành $ABDC$. $X,Y,Z$ là hình chiếu của $H$ lên $MN,ND,DM$. Chứng minh rằng đường tròn ngoại tiếp tam giác $XYZ$ tiếp xúc với đường tròn Euler của tam giác $ABC$.
Bài 2. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Đường tròn $(K)$ tiếp xúc $CA,AB$ và tiếp xúc trong $(O)$ tại $P$. Đường tròn nội tiếp $(I)$ tiếp xúc $BC$ tại $D$. $PD$ cắt trung trực $BC$ tại $Q$. Chứng minh rằng $IQ\parallel BC$.
Bài 3. Cho tam giác $ABC$ nhọn, không cân, nội tiếp đường tròn $(O)$. Đường tròn tâm $C$ bán kính $CB$ cắt $BA$ tại $D$ khác $B$ và cắt $(O)$ tại $E$ khác $B$. $DE$ cắt $(O)$ tại $F$ khác $E$. $CO$ cắt $DE,AB$ lần lượt tại $G,L$. Các điểm $M,N$ lần lượt thuộc $LE,LF$ sao cho $MG,DN$ cùng vuông góc với $BC$. Chứng minh rằng $DN=MG$.
 Đã gửi bởi
quanghung86
on 20-09-2015 - 12:49
trong
Tài liệu, chuyên đề, phương pháp về Hình học
Đã gửi bởi
quanghung86
on 20-09-2015 - 12:49
trong
Tài liệu, chuyên đề, phương pháp về Hình học
 derakynay920.pdf 125.29K
2122 Số lần tải
derakynay920.pdf 125.29K
2122 Số lần tải
 Đã gửi bởi
quanghung86
on 20-09-2015 - 23:11
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Đã gửi bởi
quanghung86
on 20-09-2015 - 23:11
trong
Thi HSG cấp Tỉnh, Thành phố. Olympic 30-4. Đề thi và kiểm tra đội tuyển các cấp.
Mình có một kinh nghiệm nhỏ về hình học là chắc chắn người ra đề khi làm đáp án không dùng đến cực đối cực và nghịch đảo, hầu như cả đề TST cũng vậy. Cho nên hai công cụ đó không cần thiết lắm và khi giải không nên nghĩ theo hướng đó. Mặt khác xu hướng làm bài hình bây giờ cũng không cần thiết góc có hướng theo nghĩa là người ra đề người ta cũng tránh ra vào cái đó.
 Đã gửi bởi
quanghung86
on 23-09-2015 - 16:59
trong
Hình học
Đã gửi bởi
quanghung86
on 23-09-2015 - 16:59
trong
Hình học
Đáp án bài 1.
Gọi $Q$ là trung điểm $HD$ dễ thấy $Q$ và $O$ đối xứng nhau qua trung điểm $P$ của $BC$ và các điểm $B,Y,H,C,D$ đều thuộc đường tròn $(Q)$ đường kính $HD$. Dễ thấy $FNH$ và $FOC$ cân nên $NH\parallel OC\parallel BQ$. Gọi $R$ là trung điểm $YD$ thì $QR\parallel NH\parallel QB$ nên $B,R,Q$ thẳng hàng. Dễ thấy các góc nội tiếp và góc so le trong bằng nhau là $\angle BDY=\angle BCY$ và $\angle BND=\angle CDN=\angle CBY$ suy ra tam giác $BYC$ và $NBD$ đồng dạng có trung tuyến tương ứng là $YP$ và $BR$. Chú ý $NH\parallel RB$ và tứ giác $HXNY$ nội tiếp nên $\angle YPB=\angle YRB=\angle HND=\angle HXY$. Tương tự $\angle ZPC=\angle HXZ$. Từ đó $\angle YPZ=180^\circ-\angle YPB-\angle ZPC=180^\circ-\angle HXY-\angle HXZ=180^\circ-\angle YXZ$. Vậy $P$ nằm trên đường tròn ngoại tiếp tam giác $XYZ$. Ta lại có $\angle NYB=360^\circ-\angle NYH-\angle HYB=180^\circ-\angle HYB+90^\circ=\angle HCB+90^\circ=\angle BCO-\angle OCH+90^\circ=$ $90^\circ-\angle BAC-NHF+90^\circ=180^\circ-\angle NHB=180^\circ-\angle NFB.$ Từ đó tứ giác $FNYB$ nội tiếp. Suy ra $\angle BFY=\angle BNY=\angle CDN=\angle CBY$. Vậy đường tròn ngoại tiếp tam giác $BFY$ tiếp xúc $BC$ tại $B$. Lại có $\angle YFH=\angle BFH-\angle BFY=\angle BHF-\angle BNY=\angle BDC-\angle CDN=\angle BDY=\angle BCY$. Từ đó đường tròn ngoại tiếp tam giác $FYC$ tiếp xúc $BC$ tại $C$. Vậy $BC$ là tiếp tuyến chung của đường tròn ngoại tiếp tam giác $YFB$ và $YFC$. Vậy $YF$ đi qua trung điểm $P$ của $BC$. Tương tự $EZ$ cũng đi qua $P$. Hơn nữa $PZ.PE=PC^2=PB^2=PY.PF$. Từ đó tứ giác $YZEF$ nội tiếp.
Gọi $K$ là tâm của đường tròn ngoại tiếp tam giác $PYZ$ và $J$ là tâm đường tròn Euler thì $PK\perp EF\perp PJ$. Từ đó $P,J,K$ thẳng hàng hay $(K)$ tiếp xúc $(J)$.
Chú ý. Tác giả bài toán tìm ra bài toán bằng phép nghịch đảo. Trong quá trình tập huấn đội tuyển KHTN thì lời giải thuần túy hình học được tìm ra. Lời giải phần chứng minh $P$ nằm trên đường tròn $(K)$ dựa trên ý tưởng của Trịnh Huy Vũ. Lời giải phần chứng minh $YF,EZ$ đi qua $P$ dựa trên ý tưởng của Trần Quang Huy. Lời giải phần chứng minh tiếp xúc dựa trên ý tưởng của Tạ Hà Nguyên.

Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học
