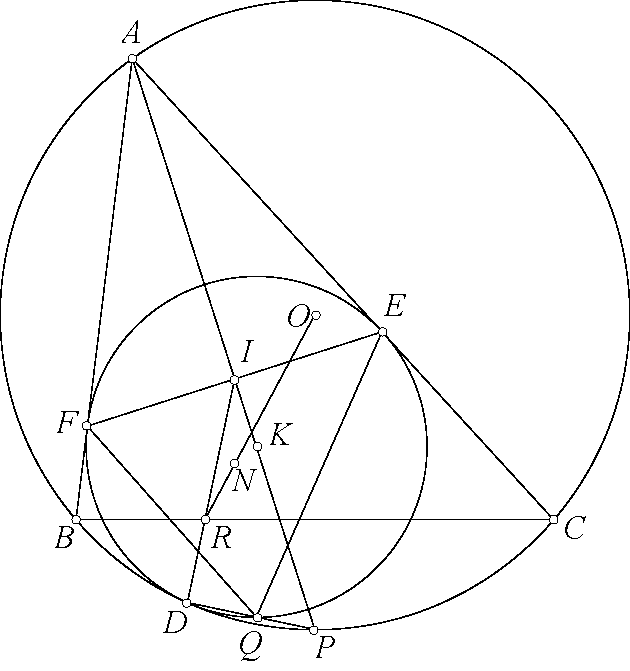Bài toán 133' của Khánh có thể viết dưới dạng tứ giác như sau

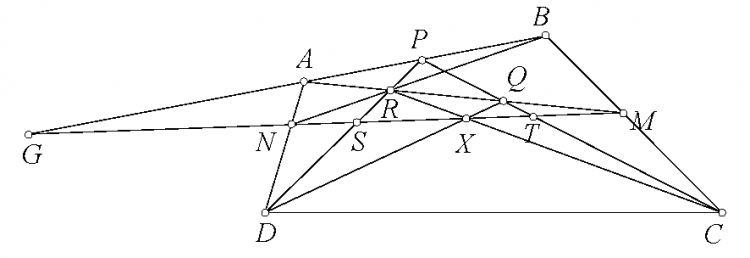
Bài toán 133'. Cho tứ giác $ABCD$ với $P,M,N$ lần lượt thuộc $AB,BC,AD$. $PC,PD$ lần lượt cắt $AM,BN$ tại $Q,R$. Chứng minh rằng $DQ,CR,MN$ đồng quy.

Giải. Gọi $MN$ cắt $ABPD,PC$ lần lượt tại $G,S,T$. Ta thấy $(PS,DR)=N(PS,DR)=(PG,AB)=M(PG,AB)=M(PT,QC)=(PT,QC)$ suy ra $DQ,CR,MN$ đồng quy.

Cảm ơn Quân và Khánh, bài toán 133 thầy chế lại từ đây http://artofproblems...nity/c6h1279917, mục đích của thầy là lấy điểm $R$ thuộc $MN$ sao cho $AR\perp EF$ rồi sau đó chứng minh $BQ,CP$ đi qua $R$ nhưng Quân chứng minh cách khác đẹp. Chú ý rằng bài toán này và bài toán của Khánh có thể đúng với $H$ bất kỳ thay vì trực tâm. Nhưng để chứng minh $AR\perp EF$ thì cần $H$ là trực tâm.

Bài toán 134. Cho tam giác $ABC$ và $DEF$ là tam giác pedal của $P$ bất kỳ. $(DEF)$ cắt $BC$ tại $G$ khác $D$. Đường thẳng qua $P$ vuông góc với $EF$ cắt $DE,DF$ tại $M,N$. Đường tròn $(DMN)$ cắt $(DEF)$ tại $Q$ khác $D$. Lấy $T$ sao cho $TM\perp AC,TN\perp AB$. $AT$ cắt $BC$ tại $S$. Chứng minh bốn điểm $A,Q,G,S$ đồng viên.

Bài toán 134 là một mở rộng của bài chọn đội tuyển Mỹ mình đã post ở đây trong #11 và các lời giải ở #12,#13 và #15.

Ta xét một bài toán tổng quát hơn của bài toán 135, có thể coi là bổ đề.

Bài toán 135'. Cho tam giác $ABC$ và $P$ nằm trong tam giác. $PA,PB,PC$ cắt $(O)$ tại $D,E,F$. $X,Y,Z$ đối xứng $D,E,F$ qua trung điểm $BC,CA,AB$. Chứng minh rằng $(XYZ)$ đi qua trực tâm $H$ của $ABC$.

Giải. Vì $D,X$ đối xứng qua trung điểm $BC$ nên hai tam giác $ABC$ và $ADX$ có chung trung tuyến hay có chung trọng tâm $G$. Từ đó $X$ là ảnh vị tự trung điểm $U$ của $AD$ qua phép vị tự tâm $G$ tỷ số $-2$. Tương tự $Y,Z$ là ảnh vị tự tâm $G$ tỷ số $-2$ của $V,W$ lần lượt là trung điểm của $BE,CF$. Dễ thấy $O,U,V,W$ nằm trên đường tròn đường kính $OP$ nên $(XYZ)$ đi qua ảnh vị tự của $O$ trong qua phép vị tự tâm $G$ tỷ số $-2$ chính là $H$. Ta hoàn tất chứng minh,

Trở lại bài toán 135. Ta chỉ cần $P$ di chuyển trên một đường thẳng cố định đi qua $A$. Gọi đường thẳng đó cắt $(O)$ tại $L$ thì đường tròn $(HRS)$ luôn đi qua đối xứng của $L$ qua trung điểm $BC$ cố định nên tâm của $(HRS)$ thuộc một đường thẳng cố định.

Mình xin đề nghị bài tiếp.

Bài toán 136. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ đường tròn bàng tiếp góc $A$ là $(J)$ tiếp xúc $BC$ tại $D$. Đường tròn qua $A,B$ tiếp xúc $(J)$ tại $M$. Đường tròn qua $A,C$ tiếp xúc $(J)$ tại $N$. $BM$ cắt $CN$ tại $P$. Chứng minh rằng $\angle PAB=\angle DAC$.

Cám ơn Hoàng về lời giải mới thú vị khác đáp án, thầy sẽ post đán án ngày mai. Xin đề nghị bài tiếp theo

Bài toán 148 (Telv Cohl). Cho tam giác $ABC$ có $P,Q$ là hai điểm đẳng giác và $E,F$ lần lượt thuộc cạnh $CA,AB$. Chứng minh rằng $ \angle BPC + \angle EPF = 180^{\circ} \iff \angle BQC + \angle EQF = 180^{\circ}$

Bài toán 148 có thể tham khảo tại đây trong #4 của Telv Cohl.

Lời giải bài toán 149.

Sử dụng định lý Desargues thì bài toán cần chứng minh tương đương với giao điểm của các cặp đường thẳng $(B_cC_b,BC);(C_aA_c,AC);(A_bB_a,AB)$ thẳng hàng khi và chỉ khi giao điểm của $(A_bA_c,BC);(B_cB_a,AC);(C_aC_b,AB)$ thẳng hàng, Gọi $B_cC_b$ và $A_bA_c$ cắt $BC$ lần lượt tại $A_3,A_4$ thì áp dụng định lý Menelaus ta thấy $\frac{A_3B}{A_3C}=\frac{B_cP}{B_cC}.\frac{C_bB}{C_bP}$ và $\frac{A_4B}{A_4C}=\frac{A_cP}{A_cC}.\frac{A_bB}{A_bP}$ do đó 

Tương tự ta có $\frac{B_3C}{B_3A}=\frac{C_aP}{C_aA}.\frac{A_cC}{A_cP}$ và $\frac{B_4C}{B_4A}=\frac{B_aP}{B_aA}.\frac{B_cC}{B_cP}$ và $\frac{C_3A}{C_3B}=\frac{A_bP}{A_bB}.\frac{B_aA}{B_aP}$ và $\frac{C_4A}{C_4B}=\frac{C_bP}{C_bB}.\frac{C_aA}{C_aP}$. 

Từ đó $\frac{A_3B}{A_3C}.\frac{B_3C}{B_3A}.\frac{C_3A}{C_3B}=\frac{B_cP}{B_cC}.\frac{C_bB}{C_bP}.\frac{C_aP}{C_aA}.\frac{A_cC}{A_cP}.\frac{A_bP}{A_bB}.\frac{B_aA}{B_aP}$

Và $\frac{A_4B}{A_4C}.\frac{B_4C}{B_4A}.\frac{C_4A}{C_4B}=\frac{A_cP}{A_cC}.\frac{A_bB}{A_bP}.\frac{B_aP}{B_aA}.\frac{B_cC}{B_cP}.\frac{C_bP}{C_bB}.\frac{C_aA}{C_aP}$

Vậy  $\frac{A_3B}{A_3C}.\frac{B_3C}{B_3A}.\frac{C_3A}{C_3B}=1/(\frac{A_4B}{A_4C}.\frac{B_4C}{B_4A}.\frac{C_4A}{C_4B})$ nên $\frac{A_3B}{A_3C}.\frac{B_3C}{B_3A}.\frac{C_3A}{C_3B}=1\iff \frac{A_3B}{A_3C}.\frac{B_3C}{B_3A}.\frac{C_3A}{C_3B}=1$.

Ta hoàn thành chứng minh.

Theo cách chứng minh bài này thì chỉ cần $B_a,C_a$ bất kỳ trên đường thẳng $PA$ là được và tương tự các điểm còn lại !

Bài toán 150 (AoPS). Cho tam giác $ABC$ với $M$, $N$, $Q$ là trung điểm $AB$, $BC$ và $AC$. $P$ nằm trong tam giác và nằm trên phân giác $\angle BCA$. Gọi $D=AP\cap MN$ và $E=BP\cap MQ$. Chứng minh rằng $MD=ME$.

Cám ơn Bảo vì lời giải rất nhanh và đẹp, theo đề nghị của em thầy để xuất tiếp bài sau

Bài toán 117. Cho lục giác lồi $ABCDEF$ thỏa mãn $AB=CD=EF$, $BC=DE=FA$ và $\angle A+\angle B=\angle C+\angle D=\angle E+\angle F$. Chứng minh rằng $\angle A=\angle C=\angle E$.

Bài toán 114 của bạn NHN có nhiều phát triển thú vị, mọi người hãy cùng quan tâm.

Cám ơn Bảo, rất vui khi thấy sự trở lại của em. Theo đề nghị của em, thầy đề nghị một bài mới như sau

Bài toán 116. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ với tâm nội tiếp $I$. Đường tròn $(K)$ tiếp xúc $CA,AB$ tại $E,F$ và tiếp xúc trong $(O)$ tại $D$. $AI$ cắt $(O)$ tại $P$ khác $A$. $PD$ cắt $(K)$ tại $Q$ khác $D$. $DI$ cắt $BC$ tại $R$. Chứng minh rằng $RO$ đi qua tâm đương tròn Euler tam giác $QEF$.

@Trong topic này những bài nào mình post mà tự sáng tác mình sẽ không ghi gì cả, còn những bài không phải của mình mình sẽ ghi rõ.

Cấu hình của bài thầy Hà trong bài đề nghị của Khánh là cấu hình rất thú vị, trên đó khai thác được khá nhiều điểm đặc biệt các tam giác $AA_bA_c,BB_cB_a,CC_aC_b$ mà những tâm đặc biệt của tam giác tạo bởi các tâm trên nằm trên đường thẳng $OI$ của $ABC$.

Mình ví dụ một bài như sau

Giữ nguyên đề của Khánh. Gọi $O_a,O_b,O_c$ là tâm ngoại tiếp tam giác $AA_bA_c,BB_cB_a,CC_aC_b$. Chứng minh rằng trọng tâm tam giác $O_aO_bO_c$ nằm trên đường thẳng $OI$ của $ABC$.

Bảo đồng ý, mình đề nghị một bài sau

$\boxed{\text{Bài toán 45.}}$ Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và tâm nội tiếp $I$. Đường tròn $(K)$ tiếp xúc $CA,AB$ tại $E,F$ và tiếp xúc trong $(O)$ tại $D$. Gọi $M,N$ là tâm ngoại tiếp tam giác $ADE,ADF$. Trung trực $CA,AB$ cắt $BC$ tại $S,T$. Trên trung trực $IA$ lấy các điểm $P,Q$ sao cho $SP\parallel AC$ và $TQ\parallel AB$. Chứng minh rằng $MP,NQ$ và $AO$ đồng quy.

Rất mong topic sẽ sôi nổi, tiến tới nếu đạt mốc 100 bài nên ra một ấn phẩm nhỏ kỷ niệm !

Bài toán mà viet nam in my heart, nói có 3 hướng tiếp cận khác nhau

- Phương pháp vector : Biểu diễn vector $\vec{XL}$ theo $\vec{XY},\vec{XZ}$ và $k$ với $\vec{OL}=k\vec{OA}$ rồi chiếu xuống $XY$.

- Hàng điều hòa: Có thể bắt chước tương tự cách chứng minh đẳng giác của điểm Nagel nằm trên đường thẳng $OI$ (của tam giác $XYZ$), giờ ta sẽ chỉ ra $XL$ là đẳng giác trong góc $X$ của $XJ$ với $J$ là một điểm xác định trên đường thẳng $OI$.

- Giải bài tổng quát hơn: chính là bổ đề đã có ở đây http://analgeomatica...1-thang-12.html

Từ đó đến bài của Bảo ta làm như sau

Gọi $U,V,W$ đối xứng $A,B,C$ qua $D,E,F$ thì $XU,YV,ZW$ đồng quy. Dễ thấy phép vị tự tâm $O$ tỷ số 3 biến đường thẳng qua trung điểm $AX$ và $D$ thành $XU$. Từ đó dễ thấy các đường thẳng mới đồng quy.

$\boxed{\text{Bài toán 78.}}$ Cho tam giác $ABC$ có các tâm bàng tiếp góc $B,C$ là $K,L$. Lấy $P,Q$ trên $CK,BL$ sao cho $LP\parallel AC,KQ\parallel AB$. $PQ$ cắt $KL$ tại $R$. $H$ là hình chiếu của $R$ lên đường thẳng $OI$ của tam giác $ABC$. $AD$ là phân giác của tam giác $ABC$. $K$ thuộc $AD$ sao cho $KH\perp HA$. $HB,HC$ cắt $(HKD)$ tại $M,N$ khác $H$. $DN,DM$ cắt $CA,AB$ tại $E,F$. Chứng minh rằng bốn điểm $A,E,H,F$ thuộc một đường tròn.

Bài tập tập huấn đội IMO 2016.

Về bài hình ngày 1 http://analgeomatica...-2015-ngay.html

Bài viết này sẽ xoay quanh và mở rộng bài hình học thi IMO năm 2014 ngày 1 bằng các công cụ hình học thuần túy.

http://analgeomatica...-hoc-trong.html