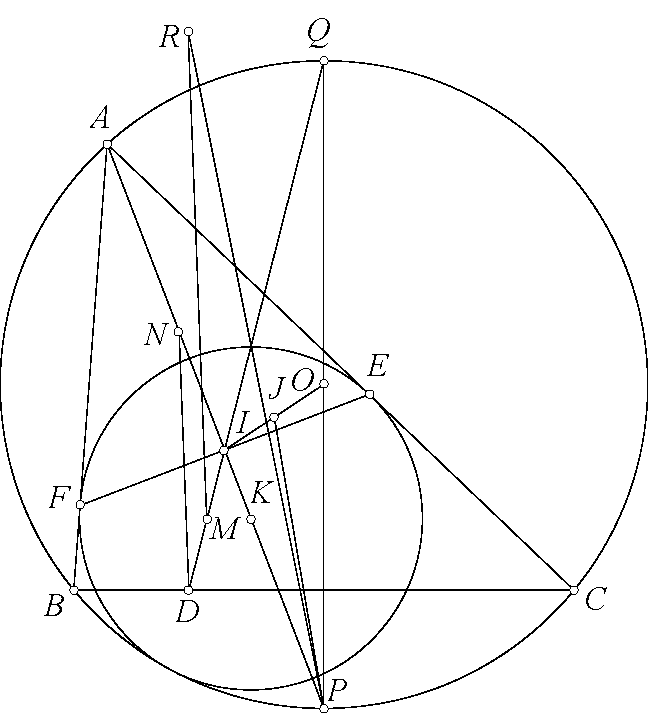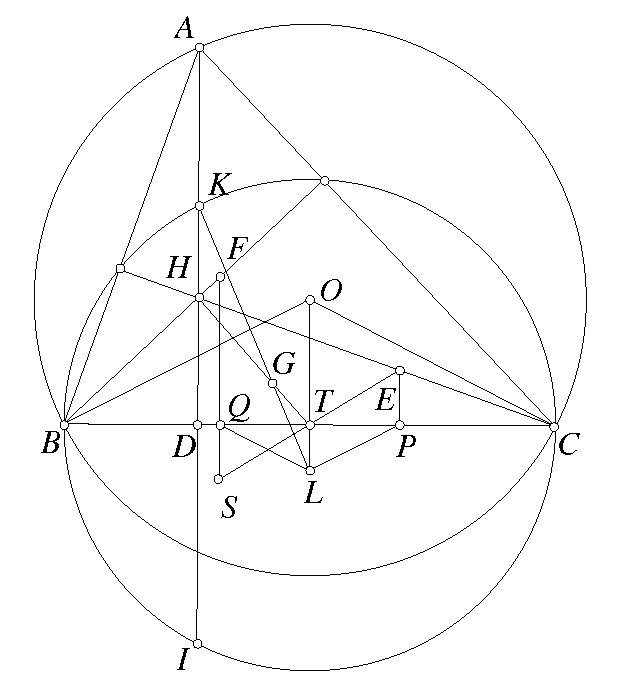Cảm ơn Quân và Bảo với các lời giải rất hay. Gốc của bài toán 126 là ở đây http://www.artofprob...munity/c6h85003, bài toán 126 có hướng phát triển theo kiểu chiếu song song nhưng khá rắc rối. Bài toán 127 cũng là bài toán hay và lạ trên hình vuông,  vietdohoangtk7nqd có thể dẫn nguồn gốc không ? Mình xin đề nghị bài tiếp

 

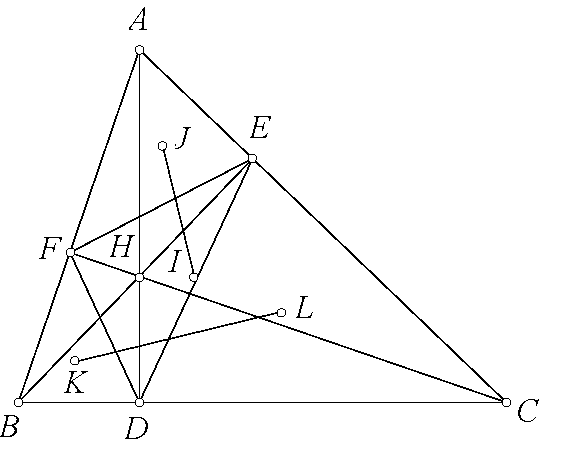
Bài toán 128. Cho tam giác $ABC$ và đường tròn $(K)$ đi qua $B,C$ cắt $CA,AB$ tại $E,F$. $BE$ cắt $CF$ tại $G$. $AG$ cắt $BC$ tại $H$. $L$ là hình chiếu của $H$ lên $EF$. $M$ là trung điểm $BC$. $MK$ cắt $(KEF)$ tại $N$. Chứng minh rằng $\angle LAB=\angle NAC$.

Cám ơn bạn, mình cũng thấy hai bài hình này của Ấn Độ nhưng vì bài toán 11 có liên quan một chút tới số học còn bài toán 10 thì hình như đã là đề Sharygin rồi nên mình lăn tăn chưa đưa lên.

 

Bài toán 10 có thể xem tại đây http://geometry.ru/o...finsols-eng.pdf bài toán 3 cho lớp 8, mình đã có một mở rộng ở đây http://www.artofproblemsolving.com/community/q2h1311625p7028614 mong mọi người quan tâm.

vietdohoangtk7nqd cần đề nghị bài tiếp nhưng vì lâu nên để bạn ấy đề nghị sau, để topic không bị gián đoán mình xin đề nghị bài tiếp

 

Bài toán 126 (AoPS). Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. $P$ nằm trên đường thẳng $OI$ của tam giác $ABC$. $X,Y,Z$ đối xứng $P$ qua $IA,IB,IC$. Chứng minh rằng $DX,EY,FZ$ đồng quy.

Cám ơn các em đã đóng góp.

 

 

Đáp án bài 125. Dựng đường tròn $(B)$ tiếp xúc $AC$. Các tiếp tuyến tại $C,A$ của $(B)$ cắt nhau tại $F$. Từ dữ kiện đề bài dễ thấy hai tam giác $\triangle EDA=\triangle BCF$ g.c.g. Từ đó $EA=BF$ mà $BE\parallel AF$ nên tứ giác $BEAF$ có thể là một hình thang cân hoặc hình bình hành. Nhưng $\angle AEB<\angle AED=\angle CBF<\angle EBF$ do đó $BEAF$ là một hình bình hành. Dễ suy ra $BCDE$ là hình bình hành.

Cám ơn em đã đóng góp xây dựng, mọi đóng góp ở mức độ nào đều là đáng trân trọng. Ai cũng phải học hỏi vì kiến thức là vô hạn kể cả trong nội tại hình học sơ cấp, thầy cũng phải luôn học tập và cố gắng hơn.

 

 

Nói qua về bài tập này http://artofproblems...c6t48f6h1368124, mình có 1 phát hiện nhỏ, nếu định nghĩa các điểm $Y,Z$ tương tự thì $IX=IY=IZ$ nói cách khác ta có thể chứng minh được $AX,BY,CZ$ đồng quy.

$(AID)$ trực giao với $(O)$ qua nghịch đảo tương đương với $I_aD$ vuông góc $BC$ với $(I_a)$ tiếp xúc $BC$ tại $D$ mà em, cái này có thể coi là hiển nhiên mà.

Topic này bị gián đoạn một chút vì bài này, thực sự mình mong muốn tìm lời giải không nghịch đảo cho nó nhưng xem ra khó có lời giải khác. Vậy mình sẽ đưa ra lời giải nghịch đảo của mình. Trước hết ta xử lý bài toán một chút.

 

Giải bài toán 124. Gọi $J$ là trung điểm $EF$ và $L$ là đối xứng của $A$ qua $OT$ thì $L$ thuộc $(O)$ và $AL$ là đường đối trung. $(S)$ là đường tròn ngoại tiếp $(AQL)$. Do đó $(Y)$ là đường tròn qua $A,J$ và trực giao với $(AQL)$. Gọi $R$ đối xứng $A$ qua $BC$ thì $(Z)$ là đường tròn qua $A,R$ và trực giao với $(AQD)$. Ta biết bài toán quen thuộc là $DP$ đồng quy với $BC$ và đường nối tiếp điểm $M,N$ của $(K)$ với $CA,AB$, gọi điểm đồng quy là $G$. Vậy ta có thể xác định $Q$ bằng cách cho $MN$ cắt $BC$ tại $G$ và $GD$ cắt $(K)$ tại $Q$. Đến đây ta chú ý rằng đường tròn $(ADI)$ luôn trực giao với $(O)$ nên tâm của $(ADI)$ luôn nằm trên $AT$. Do đó ta chỉ cần chứng minh tâm của $(ADI)$ nằm trên $YZ$ nữa thì hiển nhiên giao điểm $X$ của $YZ$ và $AT$ là tâm của $(ADI)$. Việc chứng minh tâm của $(ADI)$ nằm trên $YZ$ tương đương với việc ta cần chứng minh các đường tròn $(Y),(Z),(AID)$ đồng trục.

 

 

Nghịch đảo cực $A$ phương tích bất kỳ và sử dụng ký hiệu tương tự đồng thời viết lại bài toán với đường tròn nội tiếp, ta thu được bài toán sau

 

Bài toán 124'. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,M,N$. Đường tròn $(AMN)$ cắt $(O)$ tại $G$ khác $A$. Đường tròn $(ADG)$ cắt $(I)$ tại $Q$ khác $D$.  $L$ là trung điểm $BC$. $(K)$ là đường tròn tiếp xúc $CA,AB$ và tiếp xúc trong $(O)$. $y$ là đường thẳng qua $K$ vuông góc với $QL$ và $z$ là đường thẳng qua $O$ vuông góc với $QD$. Chứng minh rằng $y,z$ và $ID$ đồng quy.

 

Bài toán 124' đã được giải chi tiết tại đây http://artofproblems...c6t48f6h1368124

 

Để topic tiếp tục mình xin đề nghị một bài toán sau khá đơn giản

 

Bài toán 125 (Đề thi Ba Lan). Cho ngũ giác lồi $ABCDE$ với $BC=DE$ và $\angle ABE=\angle CAB=\angle AED-90^\circ$ và $\angle ACB=\angle ADE$. Chứng minh rằng $BCDE$ là hình bình hành.

 

 

 

Cảm ơn các bạn đã đóng góp tiếp tục. Về bài toán 9 mình thấy trong link có lẽ kết quả $AI\perp PQ$ thì đã quá cũ có trong nhiều sách Việt Nam, kết quả $AI=PQ$ mình cũng nhớ đã có trên TTT2. Sau đây mình xin đề xuất một bài tổng quát mình nghĩ ra và có đáp án đầy đủ

 

Mở rộng bài toán 9. Cho tam giác $ABC$ có đường cao $AD,BE,CF$ cắt nhau tại $H$. $I,J,K,L$ lần lượt là tâm nội tiếp các tam giác $ABC,AEF,BFD,CDE$. Chứng minh rằng $IJ=\frac{BF+CE}{BE+CF}KL$.

 

 

Chú ý. Kết quả trên bao hàm việc phải chứng minh $AI\perp KL$ thực chất cũng là một kết quả quen thuộc đã biết.

Bài toán 9 (INMO 2017 bài 5). Cho tam giác $ABC$ vuông tại $A$ với $AB<AC$ và đường cao $AD$. Gọi $P,Q$ và $I$ là tâm nội tiếp các tam giác $ABD,ACD$ và $ABC$. Chứng minh rằng $AI$ vuông góc và bằng $PQ$.

Đáp án bài toán 3. 1) Dễ thấy $IA$ vuông góc $EF$ tại $M$. Ta có các tứ giác $AMFL, AMEK$ nội tiếp. Chú ý $AB, AC$ tiếp xúc $(I)$ nên có các góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung bằng nhau $\angle AML =\angle AFL =\angle BFD =\angle DEF =\angle MAK$. Do đó $ML$ song song $AK$ và vuông góc $DE$. Tương tự $MK$ vuông góc $DF$ nên $M$ là trực tâm của tam giác $DKL$.

 

2) Dễ thấy $MK$ là đường trung bình của tam giác $EPF$ nên $FP$ song song $MK$ và vuông góc $DL \equiv FD$. Vậy nếu gọi $DT$ là đường kính của $I$, dễ thấy $FT$ vuông góc $FD$ nên $FP$ đi qua $T$. Tương tự $EQ$ cũng đi qua $T$. Ta có điều phải chứng minh.

Topic này là nơi dành để post các bài toán ôn tập mục đích thi vào cấp 3 chuyên toán. Một số lưu ý khi post bài như sau

 

- Nội dung các bài toán ở mức THCS. Ưu tiên các bài toán tứ giác nội tiếp vì chương trình thi chuyên cấp 3 hầu như chỉ xoay quanh tứ giác nội tiếp các điều kiện cần vả đủ.

 

- Không post bài trong các cuộc thi THCS còn hạn (như trên THTT, TTT2, PI...)

 

- Hạn chế hỏi bài tập về nhà.

 

- Post đề có nguồn gốc cụ thể.

 

Mình xin phép bắt đầu với một số đề hình học thi thử chuyên KHTN.

 

Bài toán 1 (Thi thử chuyên KHTN 2013, vòng 1, đợt 3). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định, $B, C$ cố định, $A$ di chuyển trên $(O)$. $D$ thuộc đoạn $BC$ sao cho $AD$ là phân giác $\angle BAC$. Đường tròn $(K)$ qua $A$ và tiếp xúc với $BC$ tại $D$.

 

1) Chứng minh rằng $(K)$ tiếp xúc $(O)$.

 

2) Gọi $(K)$ giao $CA, AB$ lần lượt tại $E, F$ khác $A$. $BE, CF$ lần lượt cắt $(K)$ tại $G, H$ khác $E, F$. $AG, AH$ cắt $BC$ lần lượt tại $M, N$. Chứng minh rằng độ dài $MN$ luôn không đổi khi $A$ di chuyển.

 

 

Bài toán 2 (Thi thử chuyên KHTN 2013, vòng 2, đợt 3). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. $P$ là một điểm nằm trong tam giác $ABC$. Trung trực $CA, AB$ lần lượt cắt $PA$ tại $E, F$. Đường thẳng qua $E$ song song $AC$ cắt tiếp tuyến tại $C$ của $(O)$ tại $M$. Đường thẳng qua $F$ song song $AB$ cắt tiếp tuyến tại $B$ của $(O)$ tại $N$.

 

1) Chứng minh rằng $MN$ tiếp xúc $(O)$.

 

2) Gọi $MN$ cắt dường tròn ngoại tiếp các tam giác $ACM, ABN$ lần lượt tại $Q,R$ khác $M, N$. Chứng minh rằng $BQ$ và $CR$ cắt nhau trên $(O)$.

 

 

Bài toán 3 (Thi thử chuyên KHTN 2013, vòng 1, đợt 4). Cho tam giác $ABC$, đường tròn nội tiếp $(I)$ tiếp xúc $BC, CA, AB$ lần lượt tại $D, E, F$. Gọi $K, L$ lần lượt là hình chiếu của $A$ trên $DE, DF$. Gọi $IA$ giao $EF$ tại $M$.

 

1) Chứng minh rằng $M$ là trực tâm tam giác $DKL$.

 

2) Gọi $P$ đối xứng $E$ qua $K$. $Q$ đối xứng $F$ qua $L$. Chứng minh rằng $QE, PF$ cắt nhau trên đường tròn $(I)$.

 

 

Bài toán 4 (Thi thử chuyên KHTN 2013, vòng 2, đợt 4). Cho tam giác $ABC$. Một đường tròn $(K)$ đi qua $B, C$ sao cho $(K)$ cắt đoạn $CA$ tại $E$ khác $C$ và $(K)$ cắt đoạn $AB$ tại $F$ khác $B$. $BE$ giao $CF$ tại $H$. Gọi $M$ là trung điểm $EF$. Gọi $P, Q$ lần lượt là đối xứng của $A$ qua $BE, CF$.

 

1) Chứng minh rằng đường tròn $(I)$ ngoại tiếp tam giác $HEP$ và đường tròn $(J)$ ngoại tiếp tam giác $HFQ$ cắt nhau trên $AM$.

 

2) Chứng minh rằng $(I)$ và $(J)$ có bán kinh bằng nhau.

Cám ơn Khánh và Quân, bài toán 123 là một bài không đơn giản, đáp án của thầy cũng tương tự của Khánh, lời giải của Quân khác của thầy, sau đây là đáp án bài toán 122.

 

 

Đáp án bài toán 122. ta có $A(BC,OD)=-1$. Gọi $X$ là giao điểm $GH,BC$, $N$ là giao điểm $ST,BC$. Do $A(BC,OD)=-1$ và ta có $HC\perp AB, HB\perp AC, HN\perp OA, HM\perp AD$ suy ra $H(CB,NM)=-1$ suy ra $H(BC,XN)=-1$. Suy ra $BC,XN)=-1$ suy ra $AX,BS,CT$ đồng qui. Gọi điểm đồng qui của $AX,BS,CT$ là $Q$. Ta có $(GM,EF)=A(GM,EF)=A(OD,BC)=-1$ suy ra $B(TJ,LV)+(FE,GM)=-1$ và $C(SI,KU)=(EF,GM)=-1$. Mặt khác do $J,L,V$ thẳng hàng suy ra $T(BJ,VL)=B(TJ,VL)=-1$. Chứng minh tương tự suy ra $S(CI,UK)=1$ suy ra $T(BJ,VL)=S(CI,UK)=-1$ mà $TB,SC$ cắt nhau tại $A$, $TJ,SI$ cắt nhau tại $Q$ suy ra $AQ,TV,SU$ đồng qui. Cũng có $A(BJ,VL)=S(IC,UK)=-1$ mà $TB,SI$ cắt nhau tại $B$, $TJ,SC$ cắt nhau tại $C$, suy ra $SU,TV,BC$ đồng qui. Vậy $SU,TV,BC,AQ$ đồng qui. Mặt khác theo chứng minh trên thì $AQ,BC,GH$ đồng qui. Vậy $SU,TV,GH,BC$ đồng qui.

 

Thầy đề nghị bài mới cho topic tiếp tục

 

Bài toán 124. Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. Đường tròn nội tiếp $(I)$ tiếp xúc $CA,AB$ tại $E,F$. Đường tròn $(K)$ tiếp xúc $CA,AB$ và tiếp xúc trong $(O)$ tại $D$. $AI$ cắt $(O)$ tại $P$ khác $A$. $PD$ cắt $(K)$ tại $Q$ khác $D$. Tiếp tuyến tại $A$ của $(O)$ cắt $BC$ tại $T$, $OT$ cắt trung trực $AQ$ tại $S$. Lấy điểm $Y$ nằm trên đường nối trung điểm $AE,AF$ sao cho $AY\perp AS$. Tiếp tuyến tại $A$ của $(ADQ)$ cắt $BC$ tại $Z$. $AT$ cắt $YZ$ tại $X$. Chứng minh rằng $X$ là tâm $(ADI)$.

 

Cám ơn khánh, thầy sẽ xem lại đề kỹ hơn, để topic tiếp tục, thầy đề nghị bài mới

Bài toán 123. Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$. $AB$ giao $CD$ tại $E$. $AD$ giao $BC$ tại $F$. Tiếp tuyến tại $A,C$ của $(O)$ cắt nhau tại $S$. Tiếp tuyến tại $B,D$ của $(O)$ cắt nhau tại $T$. Gọi $K,L$ là tâm ngoại tiếp tam giác $SBD$ và $TAC$. $M$ là trung điểm $EF$. Chứng minh rằng $OM\parallel KL$.

Cám ơn bạn đã đóng góp lời giải, sau đây là một mở rộng cho bài toán 8.

 

 

Mở rộng bài toán 8. Cho tam giác $ABC$ nội tiếp $(O)$. một đường tròn $(K)$ qua $B,C$ cắt $CA,AB$ tại $E,F$. $P,Q$ thuộc $(O)$ sao cho $PQ\parallel BC$. $AP,AQ$ cắt $(AEF)$ tại $R,S$. Chứng minh rằng $P,Q,R,S$ cùng nằm trên một đường tròn tâm $K$.

Cám ơn Bảo, quá nhanh và nguy hiểm , thầy đề nghị bài tiếp.

 

Bài toán 122. Cho tam giác $ABC$, trực tâm $H$, tâm ngoại tiếp $O$. Đường thẳng qua $O$ vuông góc $OA$ cắt trung trực $AH$ tại $D$. $M$ là hình chiếu của $H$ lên $AD$. $HM$ lần lượt cắt $CA,AB,OA$ tại $E,F,G$. đường thẳng qua $H$ song song $OD$ cắt $CA,AB,GC,GB$ lần lượt tại $S,T,K,L$. $SB,TC$ lần lượt cắt $CF,BE$ tại $I,J$. $IK,JL$ lần lượt cắt $MC,MB$ tại $U,V$. Chứng minh rằng $SU,TV,GH,BC$ đồng qui.

Bài toán 8 (IZHO 2017 day 1 p1). Cho tam giác $ABC$ nội tiếp $\omega$ trực tâm $H$ và $M$ là trung điểm $AB$. $P,Q$ là các điểm trên cung $AB$ không chứa $C$ của $\omega$ sao cho $\angle ACP=\angle BCQ < \angle ACQ$. Gọi $R,S$ là hình chiếu của $H$ lên $CQ,CP$. Chứng minh rằng $P,Q,R,S$ cùng nằm trên một đường tròn tâm $M$.

Ta đưa bài toán 120 về bài toán sau

 

Bài toán 120'. Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $CA,AB$ tại $E,F$. $P,Q$ lần lượt đối xứng với $E,F$ qua $IB,IC$. $K,L$ thuộc $CA,AB$ sao cho $PK\perp AB,QL\perp AC$. Chứng minh rằng đường thẳng qua $K,L$ lần lượt vuông góc $CA,AB$ cắt nhau trên đường thẳng $OI$ của $ABC$.

 

 

Lời giải. Gọi $O$ là tâm ngoại tiếp tam giác $ABC$ và $M,N$ là hình chiếu của $O$ lên $CA,AB$. Đường thẳng qua $I$ song song $BC$ cắt $OB,OC$ tại $S,T$. Dễ thấy hai tam giác $FQN$ và $CIO$ đồng dạng c.g.c mặt khác hai tam giác $FQL$ và $CIT$ đồng dạng g.g nên $\frac{LF}{LN}=\frac{TC}{TO}$. Tương tự $\frac{KE}{KM}=\frac{SB}{SO}$ do đó theo định lý Thales thì $\frac{LF}{LN}=\frac{KE}{KM}$ theo bổ đề quen thuộc dễ thấy các đường thẳng qua $K,L$ lần lượt vuông góc $CA,AB$ cắt nhau trên đường thẳng $OI$ của $ABC$.

 

Bài toán 121. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, tâm nội tiếp $I$. Đường tròn $(K)$ tiếp xúc $CA,AB$ tại $E,F$. $AI$ cắt $(O)$ tại $P$ khác $A$. $PQ$ là đường kính của $(O)$. $QI$ cắt $BC$ tại $D$. $M,N$ là trung điểm của $DI$ và $KA$. Đường thẳng qua $M$ song song $DN$ cắt trung trực $AQ$ tại $R$. Gọi $J$ là trung điểm $OI$. Chứng minh rằng $\angle APR=\angle QPJ$.

 

 

Lời giải bài toán 5. Từ $[PID]=[QID]$ thì $PD$ đi qua trung điểm $M$ của $PQ$. Mặt khác dễ thấy $PA=PD,QA=QD$ nên $A,D$ đối xứng qua $PQ$. Từ đó nếu $J$ đối xứng $I$ qua $PQ$ thì $AJ$ đi qua $M$. Vậy gọi $K$ đối xứng $I$ qua trung trực $PQ$ thì $J,K$ đối xứng qua $M$ nói cách khác $AI$ là đường đối trung của tam giác $APQ$. Từ đó tứ giác $APIQ$ điều hòa nên $QI.AP=PI.AQ$ hay $QI.DP=PI.DQ$.

Mình xin đề nghị bài tập tiếp cho topic được liên tục.

 

Bài toán 119. Cho tam giác $ABC$ có trực tâm $H$ và tâm ngoại tiếp $O$. $E,F$ là trung điểm $CA,AB$. Các điểm $M,N$ thuộc $OH$ sao cho $FM\parallel AC$, $EN\parallel AB$. $K$ là điểm thuộc $BC$ sao cho $\angle HKB=\angle OKC$. $OK$ cắt $FM,EN$ lần lượt tại $P,Q$. $MQ$ cắt $PN$ tại $R$. Chứng minh rằng $AH,OR,BC$ đồng qui.

Cám ơn Bảo về lời giải ngắn gọn, đáp án của thầy dài hơn

 

 

Đáp án bài toán 118. Gọi $T$ là trung điểm $BC$, $I$ là giao điểm thứ hai khác $K$ của $AB$ với đường tròn đường kính $BC$. Gọi $D$ là chân đường cao từ $A$ xuống $BC$ suy ra $DK=DI$ và $DK^2=DB.DC=\overline{DH}.\overline{DA}$ suy ra $(KI,AH)=-1$ nên $(KA,IH)=2$. Vậy $\dfrac{\overline{IK}}{\overline{IA}}=2\dfrac{\overline{HK}}{\overline{HA}}$ hay $\dfrac{\overline{ID}}{\overline{IA}}=\dfrac{\overline{HK}}{\overline{HA}}$ mà dễ chứng minh $\overline{HK}=2\overline{LT}$ suy ra $\dfrac{\overline{ID}}{\overline{IA}}=\dfrac{\overline{HK}}{\overline{HA}}=\dfrac{\overline{TL}}{\overline{TO}}=\dfrac{\overline{QT}}{\overline{TC}}=\dfrac{\overline{TP}}{\overline{TC}}$ suy ra $\dfrac{\overline{ID}}{\overline{DA}}=\dfrac{\overline{TP}}{\overline{PC}}$. Chứng minh tương tự thì $\dfrac{\overline{ID}}{\overline{DA}}=\dfrac{\overline{TQ}}{\overline{QB}}$ suy ra $\dfrac{\overline{TP}}{\overline{PC}}=\dfrac{\overline{TQ}}{\overline{QB}}$. Mặt khác theo định lý Thales thì $\dfrac{\overline{PE}}{\overline{PC}}=\dfrac{\overline{DH}}{\overline{DC}}$ và $\dfrac{\overline{QF}}{\overline{QB}}=\dfrac{\overline{DH}}{\overline{DB}}$. Từ đó, ta có $\dfrac{TP.TQ}{PE.QF}=\dfrac{ID^2}{DA^2}.\dfrac{DB.DC}{DH^2}=1$ suy ra $\dfrac{TP}{FQ}=\dfrac{PE}{QT}$ suy ra $\triangle PET \sim \triangle QFT$ suy ra $\angle FTQ=\angle TEP$ suy ra $\angle ETF=90^\circ$. Gọi $S$ là giao điểm $TE,QF$ suy ra $TS=TE$ và  $PE=SQ$. Mà tam giác $FES$ có đường cao $FT$ đồng thời là trung tuyến, suy ra tam giác $FES$ cân tại $F$, suy ra $FE=FS$ suy ra $FE=FS=FQ+QS=FQ+PE$. Từ đó, ta có điều phải chứng minh.

 

Đáp án bài toán 117. Gọi $BC,DE,AF$ cắt nhau tạo thành tam giác $MNP$. Vì tổng các góc của lục giác là $720^\circ$ nên $\angle A+\angle B=\angle C+\angle D=\angle E+\angle F=240^\circ$. Vì vậy, ta dễ thấy tam giác $MNP$ đều. Dựng tam giác đều $DEO$ với $O$ nằm trong lục giác. Ta thấy $EOAF$ và $DOBC$ đều là hình bình hành, nên $AB=EF=OA=CD=OB$, vậy $OAB$ là tam giác đều. Do đó, $\angle AFE+\angle BCD=\angle AOE+\angle BOD=360^\circ-60^\circ-60^\circ=240^\circ$. Nhưng do $\angle EDC+\angle BCD=240^\circ$. Từ đó suy ra $\angle AFE=\angle EDC$. Tương tự, $\angle EDC=\angle CBA$. Từ đó  $\angle B=\angle D=\angle F$. Ta có điều phải chứng minh.

Cám ơn Quân đã đóng góp lời giải, bài này thầy mở rộng từ bài IMO 2005, xin đề nghị bài tiếp như sau

 

Bài toán 118. Cho tam giác $ABC$ nhọn trực tâm $H$, tâm ngoại tiếp $O$, $G$ là trọng tâm của tam giác $HBC$. $K$ thuộc đoạn $AH$ sao cho $\angle BKC=90^\circ$. $KG$ cắt trung trực $BC$ tại $L$. Các điểm $P,Q$ thuộc đoạn $BC$ sao cho $LP\parallel OB,LQ\parallel OC$. Các điểm $E,F$ thuộc đường thẳng $HC,HB$ sao cho $PE,QF$ cùng vuông góc với $BC$. Chứng minh rằng $EF=PE+QF$.

Bài toán này là bài toán mình phát triển bài Serbia năm 2009 đã ra cho đội KHTN đã lâu, có thể dùng bài Serbia năm 2009 và bổ đề này để giải.

Một mở rộng đơn giản cho bài toán 3 nhưng có ý nghĩa.

 

Mở rộng bài toán 3. Cho tam giác $ABC$ với $M,N$ thuộc cạnh $BC$ sao cho $\angle MAB=\angle NAC$. $P$ thuộc $(ABM)$ sao cho $BP\perp AN$. Chứng minh rằng $AP$ đi qua tâm ngoại tiếp tam giác $ABC$. (Cách hỏi khác, chứng minh rằng $P$ thuộc đường thẳng cố định khi $M,N$ thay đổi).

Cám ơn Bảo vì lời giải rất nhanh và đẹp, theo đề nghị của em thầy để xuất tiếp bài sau

 

Bài toán 117. Cho lục giác lồi $ABCDEF$ thỏa mãn $AB=CD=EF$, $BC=DE=FA$ và $\angle A+\angle B=\angle C+\angle D=\angle E+\angle F$. Chứng minh rằng $\angle A=\angle C=\angle E$.

 

Bài toán 114 của bạn NHN có nhiều phát triển thú vị, mọi người hãy cùng quan tâm.