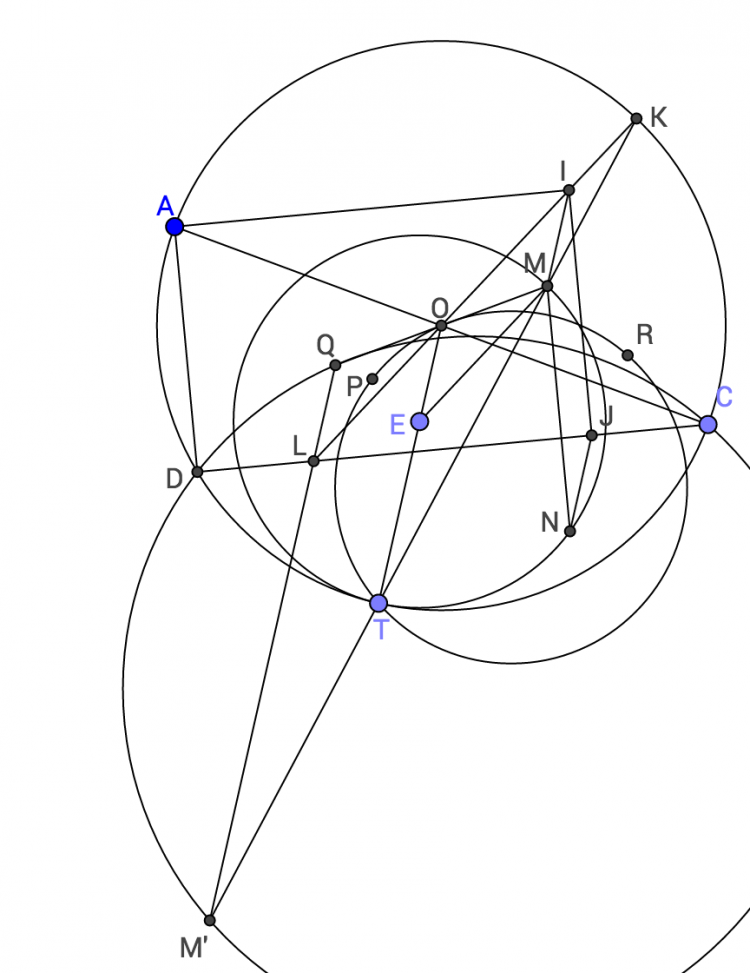
Lời giải bài toán 125.

Gọi đường thẳng qua $B,E$ vuông góc $BC,DE$ cắt $AC,AD$ ở $X,Y \Rightarrow \widehat{AEY}=\widehat{BAC}.$

Do $BC=DE \Rightarrow \Delta XBC= \Delta YED \Rightarrow XB=YE,\widehat{BXC}=\widehat{EYD} \Rightarrow \widehat{ABX}=\widehat{EAD}.$

$\Rightarrow \Delta ABX \sim \Delta EAY \Rightarrow \frac{AE}{AB}=\frac{YA}{XB}=\frac{YA}{YE} \Rightarrow \frac{\sin \widehat{ABE}}{\sin \widehat{AEB}}=\frac{\sin \widehat{AEY}}{\sin \widehat{EAD}} \Rightarrow \sin \widehat{AEB}=\sin \widehat{EAD}.$

Nếu $\widehat{AEB}+\widehat{EAD}=180^0$ thì $EB \parallel AD,$ mâu thuẫn với giả thiết ngũ giác $ABCDE$ lồi. Do đó $\widehat{AEB}=\widehat{EAD}.$

Gọi $AB$ cắt $DE$ ở $B',H$ là hình chiếu $A$ lên $DE,O'$ tâm $(AB'D).$ Khi đó:

$\widehat{B'AE}=\widehat{B'AO} \Leftrightarrow \widehat{ABE}+\widehat{AEB}=90^0-\widehat{ADE}=90^0-\widehat{ACB} \Leftrightarrow \widehat{ABE}+\widehat{AEB}=\widehat{ABC}+\widehat{BAC}-90^0$

$\Leftrightarrow \widehat{ABX}=\widehat{ABC}-90^0,$ đúng.

Vậy $\overline{A,E,O} \Rightarrow \widehat{B'AH}=\widehat{EAD}=\widehat{ABX} \Rightarrow AH \parallel BX \Rightarrow BC \parallel DE \Rightarrow BCDE$ là hình bình hành, đpcm.

Lời giải bài toán 127.

Ta thấy chỉ cần chứng minh cho trường hợp $AB=1.$ Đặt $AK=a.$

Theo định lý Thales, $\frac{AE}{AC}=\frac{AK}{AK+BC}=\frac{a}{a+1};\frac{FC}{AC}=\frac{HC}{AB+HC}=\frac{1-a}{2-a}.$

$\Rightarrow \frac{EF}{AC}=\frac{3}{2-a-a^2}-1.$

$AB=1 \Rightarrow AC= \sqrt{2}.$

Xét tam giác $A'E'F'$ có $A'E'=AE,E'F'=EF,F'A'=FC.$

Khi đó theo định lý cos:

$\cos \widehat{E'A'F'}=\frac{A'E'^2+A'F'^2-E'F'^2}{2A'E'.F'A'}=\frac{AE^2+CF^2-EF^2}{2AE.FC}.$ 

Thay các giá trị đã tính ở trên vào, ta được $\cos \widehat{E'A'F'}=\frac{1}{2} \Rightarrow \widehat{E'A'F'}=60^0.$ Ta có đpcm.

Một cách khác để chứng minh tâm của $(ADI)$ nằm trên $AT$ trong bài toán 124. :

Gọi tâm bàng tiếp góc $A$ của $\Delta ABC$ là $I_a,$ khi đó $AI.AI_a=AB.AC.$

Do đó xét phép nghịch đảo tâm $A$ phương tích $AB.AC$ hợp với phép đối xứng qua phân giác góc $A,$ ta đưa về bổ đề sau:

Bổ đề. Cho $\Delta ABC$ nội tiếp $(O),$ đường tròn bàng tiếp góc $A$ là $(I_a)$ tiếp xúc $BC$ ở $D.$

Đường thẳng qua $A$ song song với $BC$ cắt $(O)$ tại $T$ khác $A.$ Chứng minh điểm đối xứng với $A$ qua $DI_a$ là $A'$ phải thuộc $AT.$

Bổ đề này là kết quả hiển nhiên, do $AA' \perp DI_a,DI_a \perp BC,BC \parallel AT \Rightarrow AA' \parallel AT \Rightarrow \overline{A,A',T}.$

Lời giải bài toán 123.

Yêu cầu bài toán tương đương với việc chứng minh $OM$ vuông góc với trục đẳng phương của $(SBD),(TAC).$

Xét phép nghịch đảo tâm $O$ phương tích $OA^2,$ ta đưa bài toán đã cho về bài toán mới sau đây:

Bài toán 123'.Cho tứ giác $ABCD$ nội tiếp $(O),AB$ cắt $CD$ tại $E,AD$ cắt $BC$ tại $F.I,J,M$ lần lượt là trung điểm $AC,BD,EF.$ Gọi

$(\omega)$ là đường tròn đi qua $O$ và đồng trục với $(IBD),(JAC).$ Khi đó tâm của $(\omega)$ nằm trên $OM.$

Chứng minh.

Gọi $BD,AC$ cắt $EF$ tại $V,U.$ Khi đó $(DBGV)=-1 \Rightarrow GJ.GV=GB.GD=GA.GC \Rightarrow V \in (JAC).$ Tương tự $U \in (IBD).$

Gọi $O_1,O_2$ tâm $(IBD),(JAC);M'$ trung điểm $OM;O_3,M_1,M_3$ hình chiếu lên $AC$ của $O_1,M',M;O_4,M_2,M_4$ hình chiếu lên $BD$ của $O_2,M',M.$

Gọi $T,S$ là cực của $BD,AC$ với $(O);$ khi đó ta phải có $\overline{T,S,F,E},\overline{T,O_1,J,O},\overline{S,O_2,I,O}.$

Theo định lí Thales: $\frac{O_3I}{O_3M_1}=\frac{\frac{1}{2}UI}{\frac{1}{2}UM_3}=\frac{UI}{UM_3}=\frac{US}{UM}.$ Tương tự $\frac{JO_4}{JM_2}=\frac{TV}{TM}.$

Ta có $\frac{US}{UM}=\frac{TV}{TM}\Leftrightarrow \frac{VM}{TM}=\frac{SM}{UM}\Leftrightarrow MU.MV=MT.MS.$ (1)

Mặt khác, do $(UVFE)=-1=D(TSAC)=(TSFE) \Rightarrow MT.MS=ME^2=MU.MV.$ Vậy (1) đúng $\Rightarrow \frac{O_3I}{O_3M_1}=\frac{JO_4}{JM_2}.$

Lại có $O_1O_3,O_2I,M_1M'$ cùng vuông góc $AC$ và $O_2O_4,O_1J,M_2M' $ cùng vuông góc $BD \Rightarrow \overline{O_1,O_2,M'}.$

Gọi $K_1,K_2$ là giao điểm của $(IBD),(JAC),(\omega);AC$ cắt $BD$ ở $G;OG$ cắt $EF$ ở $H.$

Ta có $GB.GD=GA.GC \Rightarrow G \in K_1K_2.$ Vậy $GH.GO=GA.GB=GK_1.GK_2 \Rightarrow H \in (\omega).$

Vậy tâm của $(\omega)$ là giao điểm của trung trực $OH$ và $O_1O_2.$

Mặt khác, $M' \in O_1O_2,$ lại có $M'$ trung điểm $OM$ và $OH \perp EF \Rightarrow M'$ thuộc trung trực $OH.$

Vậy tâm của $(\omega)$ chính là $M'$ và nó nằm trên $OM,$ đpcm.

Lời giải bài toán 117.

Gọi $AF,BC,DE$ lần lượt cắt $BC,DE,AF$ tại $X,Z,Y.$ Xét $\widehat{BAF},\widehat{CBA}$ là hai góc ngoài của $\Delta XAB$ ta có:

$\widehat{X}+180^0=\widehat{BAF}+\widehat{CBA}.$ Tương tự $\widehat{Z}+180^0=\widehat{BCD}+\widehat{CDE} \Rightarrow \widehat{X}=\widehat{Z}.$

Tương tự $\widehat{X}=\widehat{Y} \Rightarrow \Delta XYZ$ đều. Gọi $O$ là điểm sao cho $AO,FO$ lần lượt song song $BC,DE.$

Khi đó $\widehat{AFO}=\widehat{Y}=60^0=\widehat{X}=\widehat{FAO} \Rightarrow \Delta AOF$ đều $\Rightarrow AO=AF=BC.$

Vậy $AO=BC,AO \parallel BC \Rightarrow AOCB$ là hình bình hành $\Rightarrow \widehat{CBA}=\widehat{COA}$ và $CO=AB=CD.$

Tương tự, $\widehat{FED}=\widehat{DOF}$ và $OD=DC \Rightarrow \Delta OCD$ đều $\Rightarrow \widehat{COD}=\widehat{AOF}=60^0.$

Do đó, $\widehat{CBA}+\widehat{DEF}=\widehat{COA}+\widehat{FOD}=240^0.$

Tương tự, $240^0=\widehat{BCD}+\widehat{AFE}=\widehat{FEY}+\widehat{Y}+\widehat{CDZ}+\widehat{Z} \Rightarrow \widehat{FEY}+\widehat{CDZ}=120^0.$

$\Rightarrow \widehat{CDE}+\widehat{DEF}=240^0=\widehat{CBA}+\widehat{DEF}\Rightarrow \widehat{CBA}=\widehat{CDE}.$

Làm tương tự với các góc còn lại, ta suy ra đpcm.

Lời giải bài toán 179.

Bổ đề 1. Cho $\Delta ABC, \Delta A'B'C'$ đồng dạng cùng hướng. Khi đó $(AB,A'B') \equiv (BC,B'C') \equiv (CA,C'A').$

Bổ đề này cơ bản, xin phép không trình bày chứng minh ở đây.

Bổ đề 2. Cho $\Delta ABC, \Delta A_2B_2C_2$ đồng dạng cùng hướng. Gọi $A_1$ là trung điểm $AA_2,$ tương tự có $B_1,C_1.$ Khi đó $\Delta A_1B_1C_1 \sim \Delta A_2B_2C_2.$

Quay lại bài toán.

Gọi $A'$ đối xứng $A$ qua $EF.$ Khi đó $\Delta A'EF= \Delta AEF \sim \Delta ABC.$ Áp dụng Bổ đề 2. cho các tam giác $A'EF,MNP,ABC$ ta suy ra $\Delta MNP \sim \Delta ABC,$ đpcm.

Bài toán 180. Cho ngũ giác $ABCDE$ lồi, điểm $F$ trên cạnh $AE$ thỏa mãn $\Delta ABC \sim \Delta CDE \sim \Delta BFD.$ Chứng minh $\frac{AF}{FE}=\frac{BF^2}{FD^2}.$

Lời giải bài toán 196. Ta chứng minh bài toán cho đường tròn $(K)$ tiếp xúc trong $(O),$ trường hợp tiếp xúc ngoài chứng minh tương tự. Ta thấy có thể bỏ đi điểm $B$ không cần thiết.

Bài toán 196'. $\Delta ADC$ vuông tại $D$ nội tiếp $(O),$ một đường tròn $(E)$ tiếp xúc trong $(O)$ ở $T.M,N \in (E)$ sao cho $MN \parallel AD$ và $MN=AD.P,R$ là trung điểm $MD,MC.$ Khi đó $P \in (ORT).$

Chứng minh. 

$M'$ đối xứng $M$ qua $T.$ Dựng điểm $I$ sao cho $OEMI$ là hình bình hành.

$OI$ cắt $(O),CD$ ở $K,L.J$ là hình chiếu $I$ lên $CD.$

Từ $OEMI$ là hình bình hành và $EM=ET$ ta suy ra được $IK=IM=JN,LK=LM$

Gọi $Q$ đối xứng $M$ qua $O$ thì $Q \in LM'.$ Ta có $LM'.LQ=LK.NJ=LK.KI=KO^2-OL^2=LC.LD \Rightarrow Q \in (M'CD).$

Qua phép vị tự tâm $M$ tỉ số $\frac{1}{2}$ ta có ngay đpcm.

Nhân dịp sắp kết thúc năm 2017 và tiến tới VMO 2018, đồng thời Marathon HH đạt mốc 200 bài, mình thay mặt BQT và các ĐHV gửi lời cảm ơn tới các thành viên của diễn đàn đã và đang theo dõi, giải bài trong Marathon HH. Sau đây là danh sách các bài toán trong Marathon chưa có lời giải.

$$\begin{array}{| l | l |} \hline Bài & Người đăng\\ \hline 162 & quanghung86\\ \hline 196 & ecchi123\\ \hline 197 & DucLuong91\\ \hline 199 & dogsteven\\ \hline 200 & SonKHTN1619\\ \hline \end{array}$$

Bài toán 182. Cho tam giác $ABC$ nhọn, nội tiếp $(O)$ và ngoại tiếp $(I).P$ là điểm bất kì trên cung nhỏ $BC.$

$M,N$ là hai điểm nằm trên cạnh $BC$ sao cho tam giác $MNP$ nhận $(I)$ làm đường tròn bàng tiếp góc $P$ và $(MNP)$ cắt lại $(O)$ ở $X.$

Chứng minh $AX$ đi qua tâm vị tự của $(O),(I).$

Lời giải bài toán 181.

Bổ đề. Cho tam giác $ABC.$ Ta luôn có $\cos A+ \cos B+ \cos C=1+ \frac{r}{R}.$

Chứng minh. Xem tại đây.

Quay lại bài toán.

Ta có $x=OB \cos A=R \cos A \Rightarrow x+y+z=R( \cos A+ \cos B+ \cos C)=R(1+ \frac{r}{R})=R+r,$ theo bổ đề. Ta có đpcm.

Hiện tại thì phần lớn các tỉnh thành trong cả nước đều đã hoàn tất kì thi chọn HSG dự thi QG, do đó mình muốn tiếp tục topic này để các mem của VMF có thể luyện tập chuẩn bị cho VMO 2017.

Mình xin đề xuất bài tiếp theo:

$\boxed{\text{Bài toán 95}}$ Cho hình chữ nhật $ABCD$ nội tiếp $(O),I$ bất kì khác $O$ nằm bên trong hình chữ nhật. $AI,BI,CI,DI$ cắt lại $(O)$ ở $A',B',C',D';M,N,P,Q$ là hình chiếu của $I$ lên $A'B',B'C',C'D',D'A'.$ Chứng minh rằng:

a) $MP \perp NQ.$

b) $(IMP),(INQ)$ trực giao.

Bài toán 94 đã lâu không có ai giải nên mình sẽ đăng cách giải bài này của mình.

$\boxed{\text{Lời giải bài toán 94}}$

Ta xét hệ trục tọa độ $Oxy$ nhận $M$ làm gốc tọa độ, trục hoành là $BC$ và trục tung là trung trực $BC$ sao cho $B,C$ lần lượt có tọa độ là $(-1;0),(1;0)$ và điểm $O$ có tung độ $2z>0.$

Khi đó phương trình đường thẳng của trung trực $OM$ chính là $y=z,$ suy ra phương trình đường thẳng của đường đối xứng với trung trực $OM$ qua điểm $O$ là $y=3z.$ Suy ra điểm $A$ có tung độ $3z.$ Gọi tọa độ của $A$ là $(t;3z).$

$A \in (O;OB) \Leftrightarrow OB^2=OA^2 \Leftrightarrow 1+4z^2 =t^2 +z^2 \Leftrightarrow t^2 -3z^2 =1.$

Vậy $A$ nằm trên conic $x^2-3y^2=1.$ Hiển nhiên conic này cố định, ta có đpcm.

$\boxed{\text{Lời giải bài toán 49}}$ Vẽ đường tròn $(Q;QA).$ Dễ thấy $(K),(L),(Q)$ có chung trục đẳng phương là $PA.$

Ta cũng thấy $N$ là tâm của đường tròn qua $A,D$ tiếp xúc $BC,$ kí hiệu nó là $(N).$ Gọi $(O)$ là đường tròn $(ABC).$

$(M)$ cắt $(N)$ tai $X$ khác $A,$ khi đó $(Q),(M),(N)$ có trục đẳng phương chung là $AX.$ Gọi $Y$ là điểm sao cho $AYBC$ là hình thang cân có đáy $AY.$

Ta có $Q \in$ trung trực $BC \Leftrightarrow OQ \perp BC \Leftrightarrow AY$ là trục đẳng phương của $(O),(Q) \Leftrightarrow APXY$ là tứ giác nội tiếp.(1)

Xét phép nghịch đảo tâm $A$ phương tích bất kì, kết hợp với (1) ta đưa bài toán ban đầu về bổ đề sau đây:

Bổ đề: Cho tam giác $ABC$ với $P$ bất kì trong tam giác $.PA,PB,PC$ cắt $(ABC)$ tại $D,E,F.$ Tiếp tuyến tại $A,P$ của $(ABC)$ lần lượt cắt $BC,EF$ tại $Y,X.$ Chứng minh $Y,P,X$ thẳng hàng.

Bây giờ ta đi chứng minh bổ đề. Gọi $Z$ là giao điểm của $AE$ và $CD.$

Áp dụng định lý Pascal cho các bộ điểm

$\begin{pmatrix} A,B,D \\ C,A,E \end{pmatrix}$ và $\begin{pmatrix} E,D,C \\ D,F,A \end{pmatrix}$ 

ta lần lượt suy ra được $X,P,Z$ thẳng hàng và $Y,P,Z$ thẳng hàng. Do đó $X,P,Y$ thẳng hàng.

Vậy bổ đề được chứng minh và bài toán gốc cũng được chứng minh.

Cá nhân mình thì mình thấy bài này cách làm khá giống bài 46, đều là nghịch đảo tâm $A$ rồi dùng Pascal, chỉ có điều bài này phức tạp hơn là phải giải quyết một phần bài toán trên hình gốc. Dẫu sao vẫn mong chờ lời giải không dùng nghịch đảo của các mem VMF cho hai bài 46 và 49         

P/s: cả 2 bài này đã có lời giải của dogsteven ở ngay dưới.

$\boxed{\text{Bài toán 50}}$ Cho một điểm $A$ bất kì và một đường thẳng $d$ không đi qua $A.$ Lấy trên $d$ các điểm $B,C,E$ sao cho đường thẳng Euler của tam giác $ABC$ song song với $AE.$ Chứng minh đường thẳng Euler của tam giác $ACE$ song song với $AB.$

Cho những ai lười bật lại bài 1 của baopbc:

$\boxed{\text{Bài toán 33}}$ Cho tam giác $ABC$ có $\angle A=60^\circ,\angle B=80^\circ$ nội tiếp $\odot (O)$, ngoại tiếp $\odot (I)$.

$AI$ cắt $OB$ tại $X$, cắt $BC$ tại $M$. Đường thẳng qua $C$ vuông góc với $AB$ cắt $OM$ tại $K$ và trung trực $BC$ tại $E.ME$ cắt $AC$ tại $L$. Đường thẳng qua $K$ vuông góc với $BC$ cắt $AC$ tại $F$. Chứng minh $(F;FK)$ tiếp xúc $(O).$

$\boxed{\text{Lời giải bài toán 27}}$ (cách khác)

Bổ đề 1: $\Delta ABC,$ một đường tròn $(O')$ qua $B,C$ cắt $AB,AC$ ở $Y,Z.BZ$ cắt $CY$ ở $H,O'H$ cắt $AX$ ở $K,U \in BC$ sao cho $UH$ tiếp xúc với $(BHC).$ Khi đó $UK$ tiếp xúc $(BKC).$

Bổ đề 2: $\Delta ABC,$ tiếp tuyến tại $A$ của $(ABC)$ cắt $BC$ ở $X.D,E \in BC.$ Khi đó $XA$ tiếp xúc $(XDE) \Leftrightarrow \widehat{BAD} = \widehat{CAE}.$

Bổ đề 2 cơ bản, xin không chứng minh ở đây. Quay lại bài toán.

$BH,CH$ cắt $AC,AB$ tại $Z,Y$ thì $BYZC$ nội tiếp $.YZ$ cắt $BC$ ở $X,$ khi đó gọi $K'$ là điểm Miquel của tứ giác toàn phần $AZCBXY$ thì $A,K',X$ thẳng hàng và $AK'$ vuông góc $K'H$ theo một kết quả quen thuộc $\Rightarrow K'$ trùng $K.$ Gọi tiếp tuyến của $H$ tại $(BHC)$ cắt $BC$ ở $U,$ theo bổ đề 1 thì $UK$ tiếp xúc $(BKC).$ Theo bổ đề 2 thì $UH$ tiếp xúc $(DHE).$ Do đó $UK^2=UB.UC=UH^2=UD.UE \Rightarrow UK$ tiếp xúc $(KDE) \Rightarrow$ đpcm.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 4\\ \hline IHateMath & 1\\ \hline fatcat12345 & 4\\ \hline dogsteven & 5\\ \hline baopbc & 7\\ \hline QuangDuong12011998 & 2\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 2\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

$\boxed{\text{Bài toán 26.}}$ Cho $\Delta ABC$ tù ở $A$ nội tiếp $(O),$ có đường cao $AH$ và đường trung bình ứng với $BC$ là $MN(M \in AB).$

$(HMN)$ cắt $(O)$ ở $P.PM,PN$ cắt $AC,AB$ ở $X,Y.$ Chứng minh $XY$ đi qua $H.$ 

Mình đề xuất 1 bài:

$\boxed{\text{Bài toán 57}}$ (geometry.ru) Cho hình thang $ABCD$ vuông tại $A,D.M,N$ trung điểm $AC,BD.(ABN),(CDM)$ lần lượt cắt $BC$ tại $Q,R.Z$ là trung điểm $MN.$ Chứng minh $ZQ=ZR.$

Mình đề xuất 1 bài:
 

$\boxed{\text{Bài toán 60.}}$ (Mathematical Reflections) Cho tam giác $ABC$ nội tiếp $(O),$ đường tròn $A-inmixtilinear$ là $(I_a)$ tiếp xúc trong $(O)$ tại $A_1.$ $A_2$ đối xứng $A_1$ qua $I_a.$ Tương tự có $B_2,C_2.$ Chứng minh $AA_2,BB_2,CC_2$ đồng quy.

@quanghung86: Chúng ta hạn chế đề xuất 2 bài nhưng hai bài này đều hay vậy hãy để cả 2 bài mọi người cùng thảo luận.

$\boxed{\text{Bài toán 81}}$ Cho tam giác $ABC,$ phân giác $BD,CE$ và tâm nội tiếp $I.$ Chứng minh $AI$ đi qua tâm đường tròn Euler của tam giác $IDE.$

chờ thầy post mà lâu quá   

$\boxed{\text{Lời giải bài toán 73}}$ 

Bổ đề 1: Cho tam giác $ABC,$ một đường tròn bất kì qua $B,C$ cắt $AB,AC$ tại $E,D.BD$ cắt $CE$ tại $G,A'$ đối xứng $A$ qua $BC.$ Khi đó $\widehat{GAB} = \widehat{GA'B}.$

Bổ đề 2: Cho tứ giác $ABCD$ nội tiếp $(O)$ có $AD$ cắt $BC$ tại $E,AC$ cắt $BD$ tại $G.(G;GE)$ cắt $AD,BC$ tại $N,M.(GND),(GMK)$ cắt nhau tại $K$ khác $G.$ Khi đó $ECKD$ là hình bình hành.

Cuối cùng, chú ý rằng bổ đề 2 chính là bài toàn ban đầu nghịch đảo tâm $E$ phương tích bất kì mà thành, ta hoàn tất chứng minh.

$\boxed{\text{Bài toán 62}}$

Cho tam giác $ABC$ có đường cao $AH$ và đường tròn nội tiếp $(I)$ tiếp xúc $AC$ ở $E.(A;AE)$ cắt $AH$ ở $M.MI$ cắt $BC$ ở $T.$

Chứng minh đường tròn đường kính $AT$ tiếp xúc với $(I).$

$\boxed{\text{Lời giải bài toán 61}}$

Trước hết, ta chứng minh $QN$ đi qua trung điểm $A_1$ của $BC.$ Gọi $QC$ cắt $AB$ tại $Z.$

Áp dụng định lý Menelaus cho tam giác $BCZ$ với các điểm $Q,A_1,N$ và tam giác $CAZ$ với các điểm $F,E,Q$ ta được: 

$Q,A_1,N$ thẳng hàng $\Leftrightarrow$ $\frac{CQ}{QZ}=\frac{NB}{NZ}$ 

$\Leftrightarrow \frac{NB}{NZ}.\frac{FZ}{FA}.\frac{AE}{EC}=1. \Leftrightarrow \frac{AB}{FA} . \frac{FZ}{NZ} =1 \Leftrightarrow \frac{FB}{FA} = \frac{NF}{FZ} (1).$

Áp dụng hệ thức lượng trong các tam giác vuông $ACN,ZCB$ ta thấy (1) đúng. Vậy tương tự ta suy ra $QN,PM,BC$ đồng quy ở $A_1.$

Theo định lý về đường thẳng Gauss của tứ giác toàn phần thì $OA_1$ đi qua trung điểm $A_2$ của $MN.$

Đường thẳng qua $A$ song song $BC$ cắt lại $(O)$ ở $J_1$ , theo tính chất của tứ giác điều hòa thì ta thấy yêu cầu của đề bài tương đương với việc chứng minh $(AJ_1,AD,AY,AX) =-1.$ (2)

Vẽ tia $A_{1}x$ song song với $MN.$

Chú ý $A_{1}x,A_{1}A_2,MA_1,NA_1$ lần lượt vuông góc $AD,AJ_1,AY,AX$ và $A_2$ trung điểm $MN,$ đồng thời $A_{1}x \parallel MN,$ ta thấy (2) đúng. Ta có điều phải chứng minh.

$\boxed{\text{Lời giải bài toán 25}}$

Bổ đề 1: $\Delta ABC$ nội tiếp $(O);M,N \in AB,AC$ sao cho $MN \parallel BC.P$ bất kì trên $(O);PM,PN$ cắt lại $(O)$ ở $X,Y.$ Khi đó $CX,BY,MN$ đồng quy tại $T$ sao cho nếu $TA$ cắt lại $(O)$ ở $P'$ thì $PP' \parallel BC.$

Bổ đề 2: $\Delta ABC$ ngoại tiếp $(I),(I)$ tiếp xúc $BC,CA,AB$ ở $D,E,F.Z$ là điểm bất kì$.DZ,EZ,FZ$ cắt lại $(I)$ ở $D',E',F'.$ Khi đó $AD',BE',CF'$ đồng quy.

Quay lại bài toán.

Theo bổ đề 1, $EX,FY,MN$ đồng quy ở $T$ và $TD$ cắt $(O)$ ở $Z$ đối xứng $P$ qua $AI.$

Theo bổ đề 2, $AZ,BX,CY$ đồng quy tại $Q$ nên suy ra đpcm.