a) Ta có $GM.GA=GB.GC=GF.GE\Rightarrow AMFE$ nội tiếp
b) Gọi I là giao của GH với AN. Giả sử (BNF) cắt (CNE) tại I'. Dễ thấy $\overline{A, N, I'}$ (tính chất quen thuộc)
Ta có NI'EC, AFI'E nội tiếp nên $\widehat{EFI'}=\widehat{EAI'}=\widehat{I'CN}$ $\Rightarrow$ GFI'C nội tiếp
Từ đây dễ cm dc $\widehat{GI'N}=90^{\circ}\Rightarrow GH\perp AN$
Mà A, E, I', F, H, M đồng viên nên $\widehat{AI'H}=90^{\circ}\Rightarrow HI'\perp AN$
$\Rightarrow$ đpcm
DaiphongLT nội dung
Có 201 mục bởi DaiphongLT (Tìm giới hạn từ 09-05-2020)
#725737 [TOPIC] ÔN TẬP HÌNH HỌC THI VÀO THPT CHUYÊN 2020-2021
 Đã gửi bởi
DaiphongLT
on 21-04-2021 - 16:23
trong
Hình học
Đã gửi bởi
DaiphongLT
on 21-04-2021 - 16:23
trong
Hình học
#726505 [TOPIC] ÔN TẬP HÌNH HỌC THI VÀO THPT CHUYÊN 2020-2021
 Đã gửi bởi
DaiphongLT
on 05-05-2021 - 18:10
trong
Hình học
Đã gửi bởi
DaiphongLT
on 05-05-2021 - 18:10
trong
Hình học
a) Ta có MN//BC, NJ phân giác ngoài $\widehat{MNC}$
$\Rightarrow \widehat{ANJ}=\widehat{ANM}+\widehat{MNC}=\widehat{ACB}+\frac{1}{2}(180^{\circ}-\widehat{ACB})=90^{\circ}+\frac{\widehat{ACB}}{2}=\widehat{AIB}$
$\Rightarrow \Delta AJN\sim \Delta ABI(g-g)\Rightarrow \frac{AJ}{AN}=\frac{AB}{AI}\Rightarrow \Delta ABJ\sim \Delta AIN(c-g-c)$
b)$\widehat{ABL}+\widehat{IAB}=2\widehat{ABJ}+\widehat{IAN}=2\widehat{AIN}+\widehat{IAN}=\widehat{AIN}+\widehat{INC}=\widehat{AIN}+\widehat{INK}$
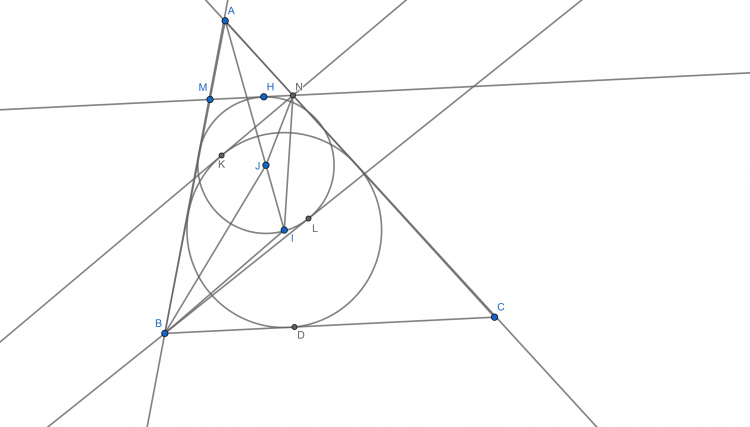
P/s: hình hơi xấu ![]()
#734566 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 22-08-2022 - 15:28
trong
Hình học
Đã gửi bởi
DaiphongLT
on 22-08-2022 - 15:28
trong
Hình học
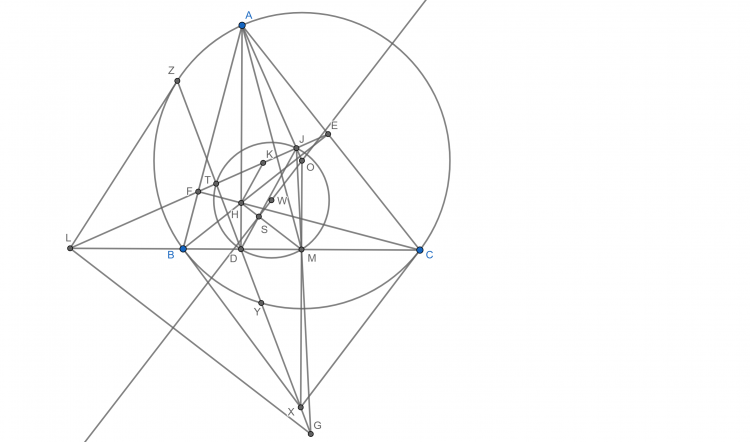
$\textbf{Bài toán 32.}$ Cho $\Delta ABC$ nhọn, không cân nội tiếp đường tròn $(O)$. Ba đường cao $AD,BE,CF$ cắt nhau tại $H$. $AO$ cắt $EF$ tại $J$. Gọi $M$ là trung điểm của $BC$. $JD$ cắt $HM$ tại $S$.a) Chứng minh rằng $OS$ đi qua tâm đường tròn ngoại tiếp $\Delta JDM$b) Giả sử $(AJD)$ cắt $(O)$ tại điểm thứ hai $K$. Gọi $I$ là điểm đối xứng với $A$ qua $(O)$, $G$ là giao điểm thứ hai của $(ADJ)$ và $(AEF)$. Chứng minh rằng $GI$ và $HK$ cắt nhau tại một điểm trên $EF$.c) Gọi $N$ là giao điểm của đường trung bình đối diện cạnh $BC$ của $\Delta ABC$ với $AD$. $ON$ cắt $(ODM)$ tại điểm thứ hai $P$. Dựng hình bình hành $DMQP$. Chứng minh rằng $Q$ thuộc đường tròn Euler của $\Delta ABC$.
$a)$, Gọi $L, T$ là giao điểm của $EF$ với $BC, HM$. $K$ trung điểm $EF$. Ta có $HK//DJ$ nên $\widehat{TJD}=\widehat{TKH}=\widehat{HMD}$ nên $TJMD$ nội tiếp. Do đó biến đổi góc đơn giản ta được $OL$ vuông góc $TD$. Gọi $X$ là giao 2 tiếp tuyến tại $B, C$ của $(O)$ thì ta được $T, D, X$ thẳng hàng. Kẻ tiếp tuyến $LX, LY$ tới $(O)$, vì $(LD, BC)=-1$ nên $X, D, Y$ thẳng hàng. Mặt khác $L, Z, J, O, M, Y$ đồng viên (đường tròn đường kính $OL$) nên nếu gọi $G$ là giao điểm của $TD$ và $JM$ thì ta có được $GY.GZ=GM.GJ$ hay $G$ nằm trên trục đẳng phương của $(JDM)$ và $(O)$, mặt khác $LD.LM=LB.LC$ nên $L$ thuộc trục đẳng phương của $(JDM)$ và $(O)$. Vì vậy $LG$ là trục đẳng phương của $(JDM)$ và $(O)$, gọi $W$ là tâm $(JDM)$ thì ta có $OW$ vuông $LG$, mặt khác $WS$ vuông $LG$ (Brocard) nên $O, W, S$ thẳng hàng.
$b)$ Gọi $HM$ cắt $EF$ tại $T$, dễ thấy $A, T, K$ thẳng hàng, gọi $GI$ cắt $EF$ tại $S$, $AS$ cắt $(JMS)$ tại $U$, ta sẽ chứng minh $T, S, U, D$ đồng viên. Phần này đơn giản là chỉ biến đổi góc, sau đó sử dụng phép nghịch đảo cực $A$ phương tích $AH.AD$ là được
$c)$ Gọi $I, J, K$ trung điểm $PM, DA, AH$. Ta có $\Delta PDM\sim \Delta DGO (g-g)$ hay $\Delta PDI \sim \Delta DGJ (c-g-c)$. Do đó $\widehat{DQM}=\widehat{PDI}=\widehat{DGJ}=\widehat{MKD}$ nên có đpcm
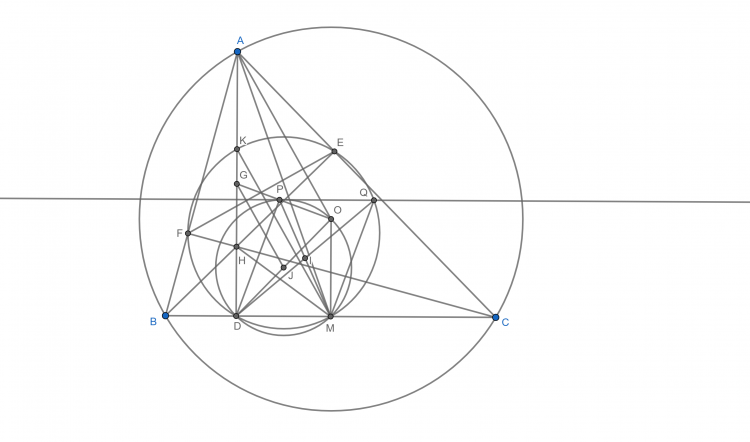
#734544 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 20-08-2022 - 22:48
trong
Hình học
Đã gửi bởi
DaiphongLT
on 20-08-2022 - 22:48
trong
Hình học
Bài 26: Cho $\Delta ABC$ nhọn nội tiếp đường tròn $(O)$ có các đường cao $AD, BE, CF$ đồng quy tại $H$. $K, L$ lần lượt là tâm $(HAB)$ và $(HAC)$. $S, T$ là hai điểm thuộc $OB, OC$ sao cho $DH$ là phân giác $\widehat{SDT}$. $X, Y$ lần lượt là trung điểm $KT, LS$. $I$ là giao điểm của đường trung tuyến đỉnh $A$ trong tam giác $ABC$ với $EF$. Chứng minh $DI$ song song với trục đẳng phương của $(X, XK)$ và $(Y, YL)$.
P/s: đây là một bài toán mình mở rộng từ một bài toán của anh Phan Quang Trí, phát biểu có vẻ dễ hơn bài ban đầu:))
Gọi $M$ trung điểm $BC$, $OM, DI$ cắt $(DEF)$ tại $N,P$. Ở đây ta dễ thấy rằng $K, L$ là điểm đối xứng của $O$ qua $AB, AC$ do đó $KL$ đi qua $N$.
Gọi $D', D'_1$ lần lượt là điểm đối xứng của $D$ qua $X, Y$. Ở đây ta dễ thấy rằng $KNCD$ là hình bình hành do đó $D'ECT$ là hình bình hành hay $D',N, E$ thẳng hàng. Tương tự ta cũng có $D'_1, N, F$ thẳng hàng.
Ta có $D'N//OC$ và $D'_1N//OB$ do đó $\widehat{D'ND'_1}=\widehat{BOC}=\widehat{EPF}$. Lại có $\frac{D'N}{D'_1N}=\frac{TC}{SB}=\frac{DC}{DB}=\frac{PF}{PE}\Rightarrow \Delta PEF\sim \Delta ND'_1D'(c-g-c)$ hay $PN//D'D'_1$. Nói cách khác $DI$ vuông góc $XY$. Từ đây ta có đpcm
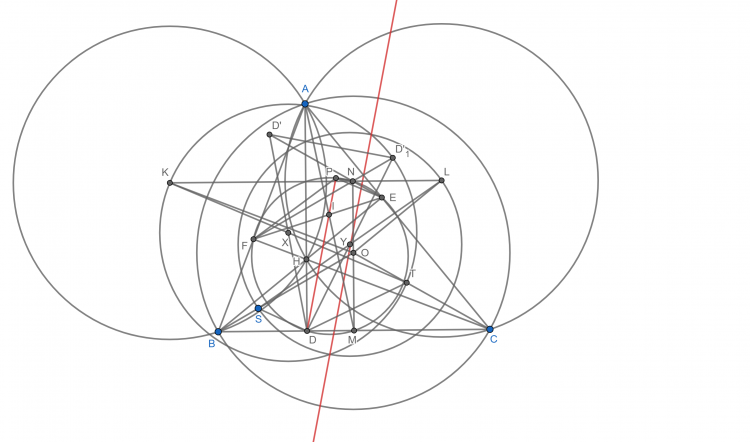
#734435 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 16-08-2022 - 13:35
trong
Hình học
Đã gửi bởi
DaiphongLT
on 16-08-2022 - 13:35
trong
Hình học
Bài 30: Cho tam giác $ABC$, trực tâm $H$. $G, N_a$ là điểm Gergone, Nagel của tam giác $ABC$. $K$ là điểm liên hợp đẳng cự với $H$ trong tam giác $ABC$. Chứng minh $GN_a$ đi qua $K$
#734577 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 22-08-2022 - 21:30
trong
Hình học
Đã gửi bởi
DaiphongLT
on 22-08-2022 - 21:30
trong
Hình học
góp vui
Bài toán 6. Trên cạnh $\displaystyle AB$ của ngũ giác $\displaystyle ABCDE$ lấy điểm $\displaystyle F$ sao cho $\displaystyle \Delta ADE\sim \Delta ECF\sim \Delta DBC$. Chứng minh rằng $\displaystyle \frac{AF}{BF} =\frac{EF^{2}}{CF^{2}}$.
Gọi $K$ là giao điểm của $AD$ và $CF$, dễ thấy $K$ thuộc $(DEC)$, định nghĩa $L$ tương tự ta cũng có $L$ thuộc $(DEC)$ hay $D, E, K, L , C$ đồng viên
Ta có $\frac{AF}{BF}=\frac{sin \widehat{AKF}.KF}{sin \widehat{DAB}}.\frac{sin \widehat{DBA}}{sin \widehat{FLB}.FL}=\frac{DA}{DB}.\frac{DC}{DE}.\frac{EF}{CF}=\frac{EF}{FC}.\frac{EC}{CF}.\frac{EF}{CE}=\frac{EF^2}{CF^2}$
#734542 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 20-08-2022 - 20:55
trong
Hình học
Đã gửi bởi
DaiphongLT
on 20-08-2022 - 20:55
trong
Hình học
để topic tiếp tục hoạt động
( vì bài trên có vẻ hơi quá tầm với mn....) mình xin post bài mới
Bài 31. Cho tam giác $ABC$ và điểm $M$ bất kỳ nằm trên trung trực $BC$. $X,Y$ là tâm đường tròn nội tiếp tam giác $ABM$ và $ACM$. Chứng minh $(AXY)$ luôn đi qua 1 điểm cố định
Xét phép nghịch đảo đối xứng cực $A$ phương tích $AB.AC$ đưa về bài toán như sau: Cho $\Delta ABC$, $M$ bất kì nằm trên đường tròn $A-Apollonius$, $X, Y$ là tâm bàng tiếp tam giác $ABM, ACM$. Chứng minh $XY$ đi qua một điểm cố định.
Ở đây $XY$ đi qua giao điểm của chân đường phân giác ngoài $\widehat{BAC}$ với $BC$
#734587 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 23-08-2022 - 13:16
trong
Hình học
Đã gửi bởi
DaiphongLT
on 23-08-2022 - 13:16
trong
Hình học
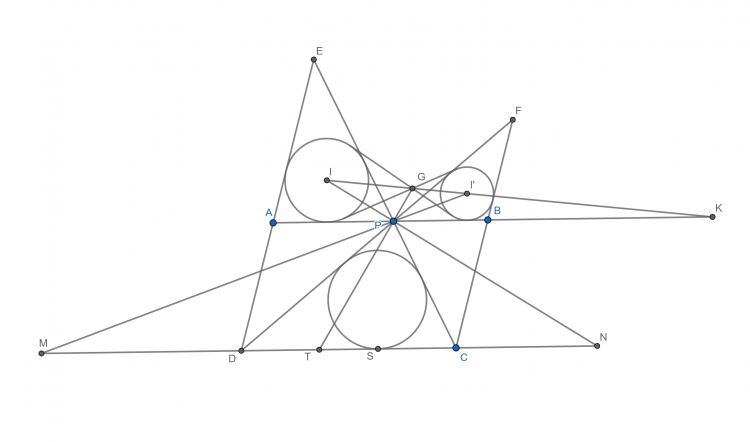
Bài 35. Cho hình bình hành $ABCD$ có $P$ là điểm bất kỳ trên $AB$. $DP,CP$ lần lượt cắt $CB$ và $AD$ tại $E,F$. $G$ là tâm vị tự trong của đường tròn nội tiếp hai tam giác $PAE$ và $PBF$. Chứng minh $PG$ đi qua điểm Nagel của tam giác $PCD$.
Gọi $I, I'$ lần lượt là tâm nội tiếp tam giác $PAE$ và $PBF$. $M, N$ lần lượt là giao điểm của $PI', PI$ với $CD$, $S$ là tiếp điểm của đường tròn nội tiếp tam giác $PCD$ với $BC$, $T$ là điểm đối xứng của $S$ qua trung điểm $CD$
Dễ thấy $DM=DP$ và $CN=CP$. Khi đó $PD-PC=SD-SC$ hay $PD+SC=SD+PC$ nên $DM+TD=TC+CN$. Do đó $TM=TN$ hay $T$ trung điểm $MN$
Gọi $II'$ cắt $BC$ tại $K$, $PT$ cắt $II'$ tại $G'$ thì ta có $(II', G'K)=P(II', G'K)=P(NM,TK)=-1$. Mặt khác $K$ là tâm vị tự ngoài của $(I)$ và $(I')$ nên $G'$ là tâm vị tự trong. Do đó có đpcm
#734657 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 27-08-2022 - 21:19
trong
Hình học
Đã gửi bởi
DaiphongLT
on 27-08-2022 - 21:19
trong
Hình học
Bài 41: Cho tam giác $ABC$, $L$ là điểm Lemoine. $E, F$ nằm trên $CA, AB$ sao cho $LE//AB$ và $LF//AC$. Đường thẳng qua $L$ song song $EF$ cắt $CA, AB$ tại $M, N$.
$a)$ Chứng minh $MNCB$ nội tiếp đường tròn $(K)$
$b)$ Chứng minh giao điểm hai tiếp tuyến tại $M, N$ của $(K)$ nằm trên $EF$
#734600 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 24-08-2022 - 00:39
trong
Hình học
Đã gửi bởi
DaiphongLT
on 24-08-2022 - 00:39
trong
Hình học
Bài 38: Cho tam giác $ABC$ $(AB<AC)$, $E$ và $F$ lần lượt nằm trên $CA, AB$ sao cho $BF=CE$, $BE$ cắt $CF$ tại $K$. $I_1, I_2$ lần lượt là tâm đường tròn nội tiếp tam giác $KBF$ và tam giác $KCE$. Phân giác trong góc $\widehat{BAC}$ cắt $I_1I_2$ tại $L$. Chứng minh $LI_1=KI_2$.
#734596 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 23-08-2022 - 20:24
trong
Hình học
Đã gửi bởi
DaiphongLT
on 23-08-2022 - 20:24
trong
Hình học
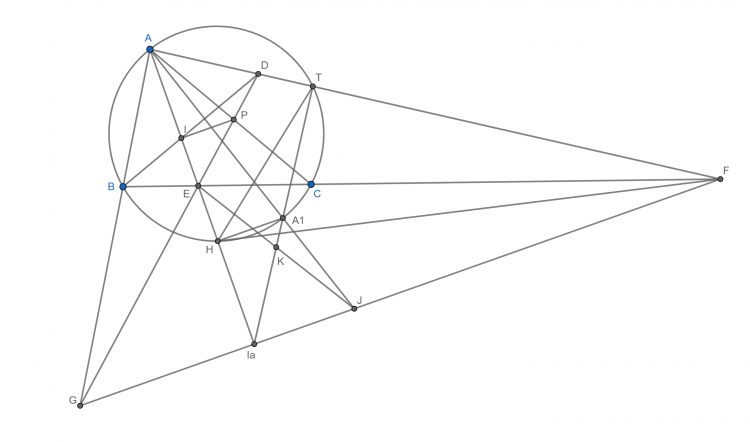
Bài 36. Cho tam giác ABC nội tiếp đường tròn (O). Gọi I, Ia lần lượt là tâm đường tròn nội tiếp, tâm đường tròn bàng tiếp góc A của tam giác ABC. Gọi AA1 là đường kính của đường tròn (O). IaA1 cắt lại đường tròn (O) tại T, AI cắt BC tại E và đường thẳng qua I vuông góc với AE cắt AC tại P. Chứng minh rằng AT, EP và BI đồng quy
Gọi $G$ thuộc $AB$ sao cho $I_aG//IP$, ta có $\Delta AI_aG \sim \Delta AIP (g-g)$ nên $\frac{I_aG}{IP}=\frac{AI_a}{AI}=\frac{EI_a}{EI}$ hay $P, E, G$ thẳng hàng. Gọi $GI_a$ cắt $AA_1$ và $BC$ tại $J$ và $F$, $I_aA_1$ cắt $EJ$ tại $K$. Menelaus cho tam giác $JEA$ cát tuyến $A_1, K, I_a$ ta sẽ được $K$ trung điểm $EJ$. Biến đổi góc đơn giản dễ thấy $AEJF$ nội tiếp. Do đó $\widehat{EAF}=\widehat{EJI_a}=\widehat{KI_aJ}=\widehat{HA_1K}=\widehat{EIT}$ hay $A, T, F$ thẳng hàng. Để ý $(AE, II_a)=-1$ nên $BI, EP, AT$ đồng quy.
#734592 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 23-08-2022 - 15:38
trong
Hình học
Đã gửi bởi
DaiphongLT
on 23-08-2022 - 15:38
trong
Hình học
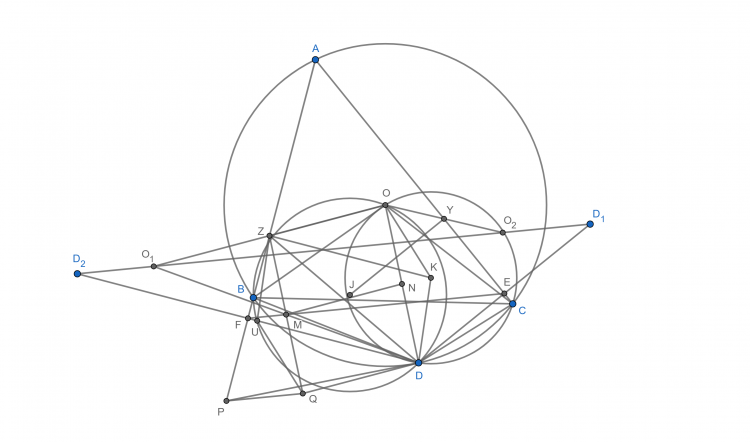
Bài 33. Cho tam giác $ABC$ nội tiếp $(O)$ và điểm $P$ bất kỳ trên $(O)$. $J,K$ là tâm đường tròn $(BOP)$ và $(COP)$. $Y,Z$ là hình chiếu của $J,K$ lên $AC,AB$. Chứng minh $YZ$ đi qua 1 điểm cố định khi $P$ di chuyển trên $(O)$
Dựng hình bình hành $OZQD$ và $DKZU$, khi đó $OKQU$ cũng là hình bình hành. Vì $KO=KD$ nên $UZ=UQ$. Gọi $(U,UV)$ cắt $AB$ tại $P$, $E$ và $F$ là hình chiếu của $D$ lên $CA$ và $AB$.
Ta có $\Delta UZQ=\Delta KOD(c-c-c)\Rightarrow \widehat{ZPQ}=\widehat{OCD}=90^{\circ}-\widehat{DAC}=\widehat{AFE}\Rightarrow PQ//EF$, mặt khác $UD//KZ$ nên $DU$ vuông $AB$ hay $D, U, F$ thẳng hàng. Do đó $Z$ và $P$ đối xứng với nhau qua $DF$. Vì vậy nếu gọi $M$ trung điểm $ZQ$ thì ta có $FM//PQ//FE$ nên $F, M, E$ thẳng hàng
Gọi $N$ trung điểm $OD$, khi đó ta có $MNOZ$ là hình bình hành, do đó nếu ta gọi $DM$ cắt $OZ$ tại $O_1$ thì ta có $ZM$ là đường trung bình của tam giác $O_1OD$. Gọi $D_1, D_2$ lần lượt là điểm đối xứng của $D$ qua $CA, AB$, vì $M$ trung điểm $OD_1$ nên $O_1$ thuộc $D_1D_2$, định nghĩa $O_2$ tương tự $O_1$, ta cũng có $O_2$ thuộc $D_1D_2$, do đó $O_1O_2$ là đường thẳng Steiner của $D$ đối với tam giác $ABC$ hay $O_1O_2$ đi qua trực tâm tam giác $ABC$. Đến đây xét phép vị tự tâm $O$, tỉ số $\frac{1}{2}$, ta được $YZ$ đi qua tâm Euler của tam giác $ABC$
#734402 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 15-08-2022 - 17:11
trong
Hình học
Đã gửi bởi
DaiphongLT
on 15-08-2022 - 17:11
trong
Hình học
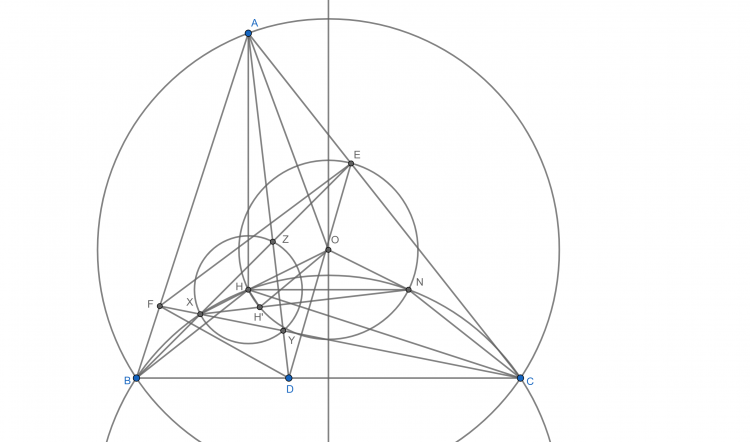
Bài 28. Cho tam giác $ABC$ nhọn và điểm $D$ bất kỳ di động trên $BC$ sao cho $AD$ không vuông góc $BC$. Giả sử tồn tại hai điểm $E,F$ trên $AC,AB$ sao cho $\angle ADB = \angle BEC = \angle CFA$. $AD,BE,CF$ cắt nhau tạo thành tam giác $XYZ$. Chứng minh trực tâm tam giác $XYZ$ di động trên 1 đường tròn cố định khi $D$ di động
Gọi $O, H$ lần lượt là tâm ngoại tiếp, trực tâm tam giác $ABC$, $H'$ là trực tâm giác $XYZ$. Dễ thấy $\Delta XYZ\sim \Delta ABC(g-g)$
Dễ chứng minh được $X, Y, Z$ thuộc $(BHC), (CHA), (AHB)$. Do đó $H$ là tâm $(XYZ)$
Gọi $N$ là điểm đối xứng của $H$ qua trung trực $BC$. Khi đó ta có $(XN, XH)$ $+$ $(XH, AD)$ $\equiv$ $(CN,CH)$ $+$ $(AO,CB)$ $\equiv$ $(CN,CB)$ $-$ $(CH, CB)$ $+$ $(AO,CB)$ $\equiv$ $(CA,CB)$ $+$ $(CB,BH)$ $\equiv$ $\frac{\pi }{2}$ (mod $\pi$)
Vì vậy $XN$ vuông $AD$ hay $X, H', N$ thẳng hàng. Ở đây $\Delta AHO\sim \Delta XH'H$ nên $(H'H, H'X)=(HO,HA)=\frac{1}{2}(OH,ON)$ (mod $\pi$) hay $H'$ nằm trên $(O,OH)$.
#734359 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 13-08-2022 - 13:57
trong
Hình học
Đã gửi bởi
DaiphongLT
on 13-08-2022 - 13:57
trong
Hình học
Bài 26: Cho $\Delta ABC$ nhọn nội tiếp đường tròn $(O)$ có các đường cao $AD, BE, CF$ đồng quy tại $H$. $K, L$ lần lượt là tâm $(HAB)$ và $(HAC)$. $S, T$ là hai điểm thuộc $OB, OC$ sao cho $DH$ là phân giác $\widehat{SDT}$. $X, Y$ lần lượt là trung điểm $KT, LS$. $I$ là giao điểm của đường trung tuyến đỉnh $A$ trong tam giác $ABC$ với $EF$. Chứng minh $DI$ song song với trục đẳng phương của $(X, XK)$ và $(Y, YL)$.
P/s: đây là một bài toán mình mở rộng từ một bài toán của anh Phan Quang Trí, phát biểu có vẻ dễ hơn bài ban đầu:))
#733753 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 21-06-2022 - 22:43
trong
Hình học
Đã gửi bởi
DaiphongLT
on 21-06-2022 - 22:43
trong
Hình học
Hic mọi người giải nhanh quá
Đây là bài toán sau khi đảo mô hình nhưng vẫn có lời giải với suy nghĩ tự nhiên!
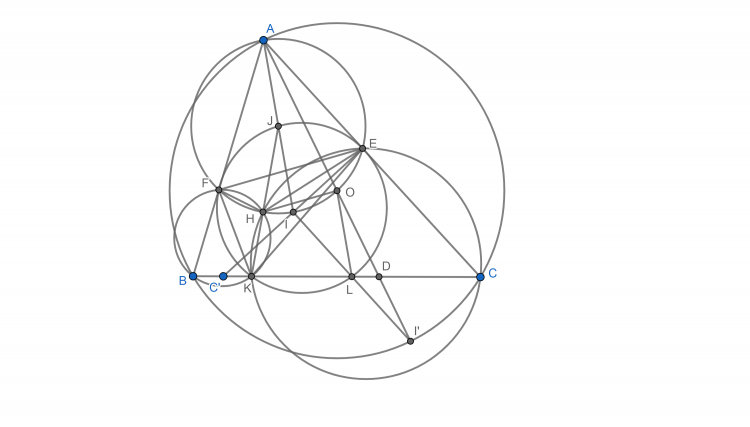
Bài toán 10. Cho $\Delta ABC$ nội tiếp $(O)$, $H$ là trực tâm của tam giác. Gọi $J$ là tâm $(AOH)$.$JH$ cắt $BC$ tại $K$. $L$ thuộc $BC$ sao cho $OL//AJ$. Chứng minh rằng $(JKL)$ và $(J)$ cắt nhau trên $AC$. (Hiển nhiên do tính đối xứng nên hai đường tròn vẫn cắt nhau trên $AB$)
Gọi $AO$ cắt $BC$ tại $D$. Biến đổi góc đơn giản ta có $\widehat{JHO}=\widehat{ADB}$ nên $HODK$ nội tiếp
Gọi $(BHK), (CHK)$ cắt $AB, AC$ tại $F, E$
Ta có $\widehat{AEH}=\widehat{HKC}=\widehat{AOH}$ nên $F\in (AOH)$. Tương tự với điểm $E$, do đó $A, E, O, H, F$ đồng viên
Dễ thấy $JFKE$ nội tiếp. Định nghĩa lại $L$, là giao điểm thứ hai của $(KEF)$ với $BC$.
Kẻ đường cao $AX, BY, CZ$ thì ta dễ chứng minh được $\Delta KEF\sim \Delta XYZ(g-g)$
Do đó biển đổi góc ta dễ chứng minh được $LB=LF, LC=LE$
Kẻ đường kính $AI$ của $(AOH)$, $I'$ đối xứng với $I$ qua $L$
Gọi $C'$ đối xứng với $C$ qua $L$, khi đó ta có $C', I, E$ thẳng hàng. Do đó $\widehat{ACI'}=90^{\circ}$, tương tự $\widehat{ABI'}=90^{\circ}$
Do đó $AI'$ là đường kính của $(O)$. Đến đây dễ chứng minh $AJLO$ là hình bình hành hay $L$ thỏa mãn giả thiết ban đầu. Đpcm
#733725 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 20-06-2022 - 16:08
trong
Hình học
Đã gửi bởi
DaiphongLT
on 20-06-2022 - 16:08
trong
Hình học
Bài toán 8: Cho $\Delta ABC$ ngoại tiếp $(I)$, $(I)$ tiếp xúc với $BC, CA, AB$ tại $D, E, F$. $T$ là điểm thuộc $(I)$ sao cho $(BTC)$ tiếp xúc với $(I)$ tại $T$. $AT$ cắt $(BTC)$ tại $S$. Chứng minh $P, I, D, S$ đồng viên.
P/s: Đây có thể coi là bài toán sau khi nghịch đảo của bài 5, nhưng giải bằng hình học thuần túy vẫn được
#733717 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 20-06-2022 - 11:04
trong
Hình học
Đã gửi bởi
DaiphongLT
on 20-06-2022 - 11:04
trong
Hình học
Bài toán 4: Cho tam giác ABC, hai điểm P, Q đẳng giác trong tam giác ABC. Gọi D, E, F; X, Y, Z lần lượt là hình chiếu của P, Q trên BC, CA, AB. EF cắt BC tại G. Khi đó PG vuông góc với AX.
Bài này mình tổng quát từ một bài toán đơn giản, chắc cũng có ở đâu đó rồi
Gọi hình chiếu của $P$ lên $AX$ là $H$
Thì khi đó ta có $A, E, P, H, F$ đồng viên hay $EFPH$ nội tiếp
Do đó áp dụng định lý về tâm đẳng phương ta có $EF$, $PH$, $BC$ đồng quy
#733716 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 20-06-2022 - 10:52
trong
Hình học
Đã gửi bởi
DaiphongLT
on 20-06-2022 - 10:52
trong
Hình học
Bài toán 2. (Trần Quang Hùng) Cho $\Delta ABC$ nhọn có $AB<AC$. Ba đường cao $AD,BE,CF$ cắt nhau tại $H$. $DE,DF$ cắt $AB,AC$ tại $P,Q$. Gọi $R$ là trung điểm của $PQ$. $OH$ cắt $AR$ tại $L$. Gọi $N$ là tâm đường tròn Euler của $\Delta ABC$. Chứng minh rằng trực tâm của $\Delta ALN$ nằm trên $EF$.
Gọi $I, G$ lần lượt là trung điểm $CA, AB$. $J$ là giao điểm của $GI$ và $EF$. $L'$ là giao điểm của $GE$ và $FI$.
Ta dễ thấy $L'$ nằm trên đường thẳng $Euler$ của $\Delta ABC$
Ta có: $QA.QC=QF.QD$ nên $Q$ thuộc trục đẳng phương của $(O)$ và $(N)$, tương tự cho điểm $P$
Do đó $PQ$ là trục đẳng phương của $(O)$ và $(N)$ suy ra $PQ\perp OH$. Mặt khác dễ thấy $AJ\perp OH$ nên $AJ// PQ$
Gọi $AJ$ cắt $EF$ tại $K$ thì ta có $(L'K, GE) = -1$
$AK//PQ$ nên $A(RK, PQ) = -1$ hay $(LK, GE) = -1$
Do đó $L'$ trùng $L$. Theo định lí $Brocard$ ta có $J$ là trực tâm tam giác $ALN$
P/s: Bài 1 có thể bỏ điểm $H$, lấy một điểm $X$ bất kì nằm trên tiếp tuyến tại $A$ của $(O)$, sau đó định nghĩa $K$ là giao của đường qua $A$ vuông với $OX$ với $BC$ thì bài toán vẫn đúng

#733765 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 22-06-2022 - 21:01
trong
Hình học
Đã gửi bởi
DaiphongLT
on 22-06-2022 - 21:01
trong
Hình học
$JS$ cắt $IE, AE, BC$ tại $M,T,D$
Đầu tiên ta dễ thấy $ASTI$ nội tiếp
Do đó $TI//BC$. Mặt khác $JI^2=JD.JS$ do đó ta có được $ID//TE$
Từ đó ta có được $ITED$ là hình bình hành hay có đpcm.
#733789 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 25-06-2022 - 09:18
trong
Hình học
Đã gửi bởi
DaiphongLT
on 25-06-2022 - 09:18
trong
Hình học
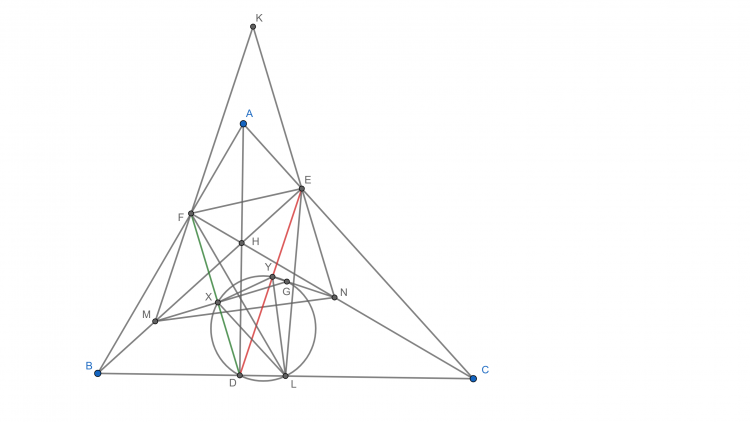
Bài 14. Cho tam giác $\displaystyle ABC$ nhọn, $\displaystyle BE,CF$ là các đường cao của tam giác đó. Trên $\displaystyle BE,CF$ lấy $\displaystyle M,N$ sao cho $\displaystyle EF=MF=NE$. $\displaystyle MF$ cắt $\displaystyle NE$ tại $\displaystyle K$. Chứng minh trực tâm của $\displaystyle KMN$ nằm trên trung trực $\displaystyle BC$.
Dễ thấy $FM//ED, EN//FD$. Gọi $X, Y$ lần lượt là hình chiếu của $M, N$ lên $FD, ED$
Khi đó dễ chứng minh được $\Delta FMX\doteq \Delta ENY(g-c-g)$ nên $FX=EY$ $(1)$
Gọi $L$ trung điểm $BC$ thì $L$ thuộc $(DEF)$ và $LE=LF$ $(2)$
Từ $(1), (2)$ suy ra $L$ thuộc $(DXY)$
Gọi $MX$ cắt $NY$ tại $G$ thì $G$ là trực tâm $\Delta KMN$ và $G$ thuộc $(DXY)$. Do đó $D, X, Y, G, L$ đồng viên hay $GL$ vuông $BC$. Đpcm
#734358 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 13-08-2022 - 13:45
trong
Hình học
Đã gửi bởi
DaiphongLT
on 13-08-2022 - 13:45
trong
Hình học
Một bài toán mình được học thấy khá hay, có thể mọi người từng gặp:
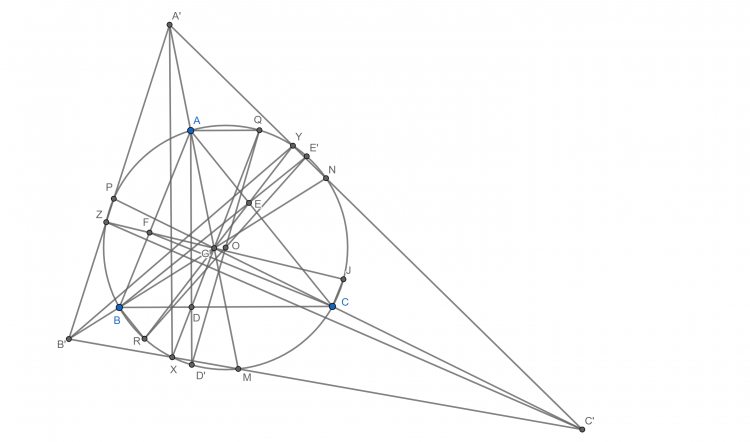
Bài 25: Cho tam giác $ABC$ không cân nội tiếp $(O)$, trọng tâm $G$. Kẻ ba đường cao $AD,BE,CF$. Các tia $GD,GE,GF$ cắt $(O)$ tại $X,Y,Z$, $AG,BG,CG$ cắt $(O)$ tại $M,N,P$. Các đường thẳng $MX,NY,PZ$ cắt nhau tạo thành tam giác $A'B'C'$. Chứng minh rằng $A'X, B'Y, C'Z$ cắt nhau tại một điểm nằm trên đường thẳng $OG$.
Đầu tiên ta sẽ chứng minh $AX, BY, CZ$ đồng quy
Gọi $Q$, $R$ là các điểm thuộc $(O)$ thoả mãn $AQ//BC$ và $BR//AC$. Dễ thấy $X, D, G, Q$ và $Y, E, G, R$ thẳng hàng
Gọi $AD, BE$ cắt (O) tại $D', E'$. Pascal $\begin{pmatrix} A & Y& Q \\ B & X& R \end{pmatrix}$ và $\begin{pmatrix} A & Q& E' \\ B & R& D' \end{pmatrix}$. Ở đây ta dễ thấy $QD'$ và $RE'$ đều đi qua $O$. Do đó ta có được giao điểm của $AX$ và $BY$ là một điểm thuộc đường thẳng Euler. Chứng minh tương tự, ta được $AX, BY, CZ$ đồng quy tại một điểm thuộc đường thẳng Euler.
Quay lại bài toán, định nghĩa $J$ tương tự $Q, R$. Pascal $\begin{pmatrix} P&Y &B \\ N&Z &C \end{pmatrix}$ và $\begin{pmatrix} Y &B& J\\ Z &C& R \end{pmatrix}$. Ở đây giao điểm của $BR$ và $CJ$ là điểm đối xứng với $A$ qua trung điểm $BC$. Vì vậy ta có được $A', A, G$ thẳng hàng. Tương tự ta thu được $AA', BB', CC'$ đồng quy tại $G$.
Do đó $\frac{XB'}{XC'}=\frac{sin\widehat{BGD}}{sin\widehat{CGD}}.\frac{GB'}{GC'}=\frac{BD}{CD}.\frac{GC}{GB}.\frac{GB'}{GC'}$. Tương tự cho các cặp còn lại, ta có được $A'X, B'Y, C'Z$ đồng quy. Desargues cho $\Delta A'AX$ và $\Delta C'CZ$ ta thu được giao điểm của $A'X$ và $C'Z$ là một điểm thuộc đường tròn Euler (theo phần chứng minh ở trên). Do đó ta có được đpcm
#734138 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 29-07-2022 - 23:47
trong
Hình học
Đã gửi bởi
DaiphongLT
on 29-07-2022 - 23:47
trong
Hình học
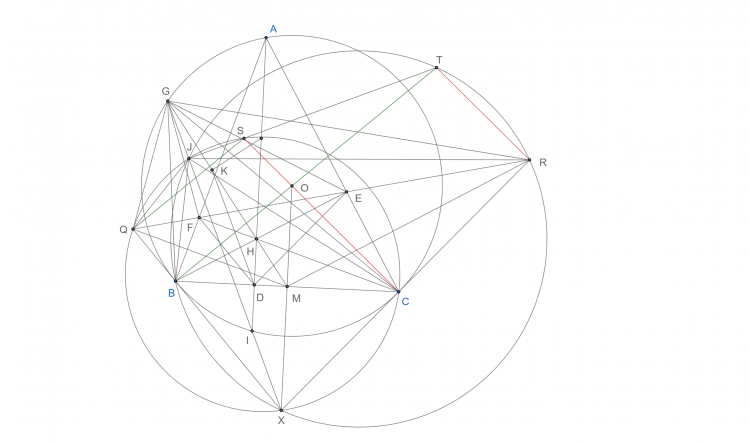
Bài toán 23. Cho tam giác $ABC$ nhọn với đường cao $AD,BE,CF$ đồng quy tại $H$. $M$ là trung điểm $BC$. Trên $EF$ lấy các điểm $Q,R$ sao cho $MQ⊥AB$ và $MR⊥AC$. Lấy các điểm $S,T$ sao cho $CS||RT⊥DE$, $QS||BT⊥DF$. $K$ là hình chiếu của trung điểm $AH$ lên $HM$. Chứng minh $DK⊥ST$
Gọi $QB$ cắt $CR$ tại $X$, dễ thấy $QB, CR$ lần lượt là tiếp tuyến của đường tròn $(O)$ nên $\widehat{SQB}= \widehat{TRC}=90^{\circ} \Rightarrow$ $SQXC, TRXB$ nội tiếp
Gọi $AH$ và $MH$ cắt $(O)$ tại $I$ và $G$ như hình vẽ. Khi đó $K$ là trung điểm $GH$
Gọi $J$ là giao điểm thứ hai của $(XQC)$ và $(XBR)$ $\Rightarrow$ $\Delta JQB\sim \Delta JCR(g-g)\Rightarrow \frac{JQ}{JC}=\frac{QB}{CR}$
Biến đổi góc đơn giản dễ thấy $G, Q, B, M, E$ nên $\Delta GQB\sim \Delta GFH(g-g)\Rightarrow \frac{GQ}{QB}=\frac{GF}{FH}$
Tương tự $G, R, C, M, F$ đồng viên nên $\Delta GRC\sim \Delta GEH(g-g)\Rightarrow \frac{GR}{CR}=\frac{GE}{EH}$. Mà $(GH, FE)=-1$ nên $\frac{GF}{FH}=\frac{GE}{EH}$ nên $\frac{GQ}{QB}=\frac{GR}{CR}$$\Leftrightarrow \frac{GQ}{GR}=\frac{QB}{CR}=\frac{JQ}{JC}$
Biến đổi góc ta cũng dễ chứng minh được $GQXR$ nội tiếp do đó ta có được $\Delta GQR\sim \Delta JQC(c-g-c)\Rightarrow \widehat{JXQ}=\widehat{JCQ}=\widehat{GRQ}=\widehat{GXQ}\Rightarrow$ $G, J, I, X$ thẳng hàng hay $IG$ là trục đẳng phương của $(XQC)$ và $(XBR)$
$\Rightarrow IG\perp ST$ hay $DK\perp ST$
#733816 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 28-06-2022 - 10:06
trong
Hình học
Đã gửi bởi
DaiphongLT
on 28-06-2022 - 10:06
trong
Hình học
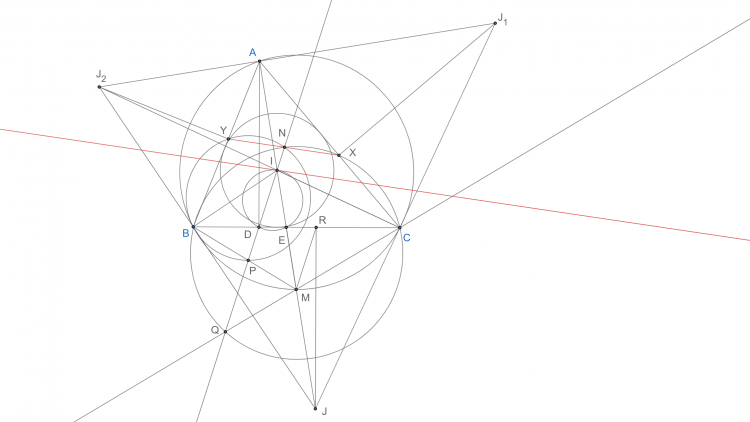
Bài toán 20. Cho tam giác $ABC$ có $I$ là tâm nội tiếp. Đường tròn bàng tiếp góc $B,C$ lần lượt tiếp xúc với $AC,AB$ tại $X,Y$. Gọi $AD,AE$ là đường cao và đường phân giác của tam giác $ABC$. Chứng minh $DE$song song với tiếp tuyến tại $I$ của $(IDE)$.
Gọi $(J)$ là đường tròn bàng tiếp góc $A$, $R$ là hình chiếu của $J$ lên $BC$, $AI$ cắt $(O)$ tại $M$
Ta có $\Delta MBE\sim \Delta MAB(g-g)\Rightarrow \frac{MB}{ME}=\frac{BA}{BE}\Leftrightarrow \frac{MJ}{ME}=\frac{IA}{IE}\Leftrightarrow \frac{EJ}{EM}=\frac{EA}{EI}\Leftrightarrow \frac{EI}{EM}=\frac{EA}{EJ}=\frac{ED}{ER}$
$\Rightarrow ID//MR$. Gọi $ID$ cắt $MB, MC$ tại $P, Q$
Ta có $DP//MR$ nên $\frac{BM}{MP}=\frac{BR}{DR}$ $(1)$, $QD//MR$ nên $\frac{CM}{MQ}=\frac{CR}{RD}$ $(2)$
Từ $(1)$ và $(2)$ ta có được $\frac{MP}{MQ}=\frac{CR}{BR}=\frac{AY}{AX}$. Do đó $\Delta MPQ\sim \Delta AYX(c-g-c)$
Gọi $ID$ cắt $XY$ tại $N$ thì suy ra $\widehat{AYN}=\widehat{MPQ}=\widehat{NPB}$ hay $YNPB$ nội tiếp
$\Rightarrow \widehat{YNI}=180^{\circ}-\widehat{ABM}=\widehat{IED}$. Do đó có đpcm
#733804 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 27-06-2022 - 09:22
trong
Hình học
Đã gửi bởi
DaiphongLT
on 27-06-2022 - 09:22
trong
Hình học
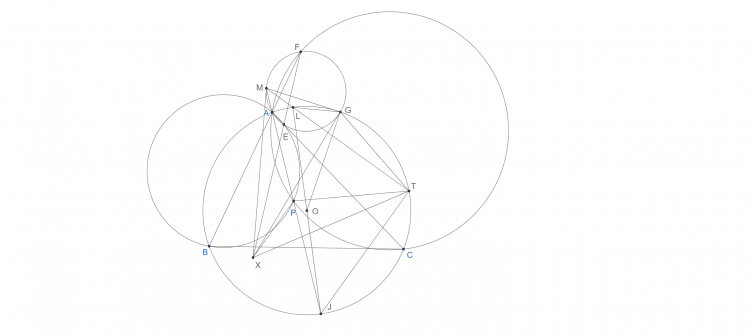
Bài toán 17. Cho tam giác $ABC$ với $P$ là điểm bất kỳ. Đường tròn $(PAB),(PAC)$ cắt $CA,AB$ tại $E,F$. Đường tròn $(AEF)$ cắt $AP$ tại $M$. Tiếp tuyến tại $M$ của $(AEF)$ cắt EF tại $X$. Chứng minh đối xứng của $M$ qua $XP$ nằm trên $(ABC)$.
Gọi $AP$ cắt $(O)$ tại $J$, $L$ đối xứng với $J$ qua $O$, $ML$ cắt $(O)$ tại $T$, $(AEF)$ cắt $(O)$ tại $G$
Dễ thấy $\frac{GB}{GC}=\frac{GF}{GE}=\frac{CF}{BE}=\frac{JB}{JC}$ nên $GJB$ là tứ giác điều hòa
$\Rightarrow A(GM, EF)=-1$ hay $XG$ cũng là tiếp tuyến của $(AEF)$
$\Delta MFG\sim \Delta JBG (g-g)\Rightarrow \widehat{MFG}=\widehat{JBG}=\widehat{OLG}\Leftrightarrow \widehat{XMG}=\widehat{OLG}$
$\Rightarrow \Delta XMG\sim \Delta OLG(g-g)\Rightarrow \widehat{LOG}=\widehat{MXG}\Leftrightarrow \widehat{MGT}=\frac{1}{2}\widehat{LOG}=\frac{1}{2}\widehat{MXG}$ nên $T$ thuộc $(X, XM)$ hay $XT=XM$
Một tính chất khá quen thuộc là $PM=PJ$ (phần này có ở bài 3.34 sách thầy Nguyễn Văn Linh các bạn có thể tham khảo)
Mà $\widehat{MTJ}=90^{\circ}$ nên $PT=PM$. Do đó có đpcm
#734363 [TOPIC] HÌNH HỌC PHẲNG
 Đã gửi bởi
DaiphongLT
on 13-08-2022 - 18:14
trong
Hình học
Đã gửi bởi
DaiphongLT
on 13-08-2022 - 18:14
trong
Hình học
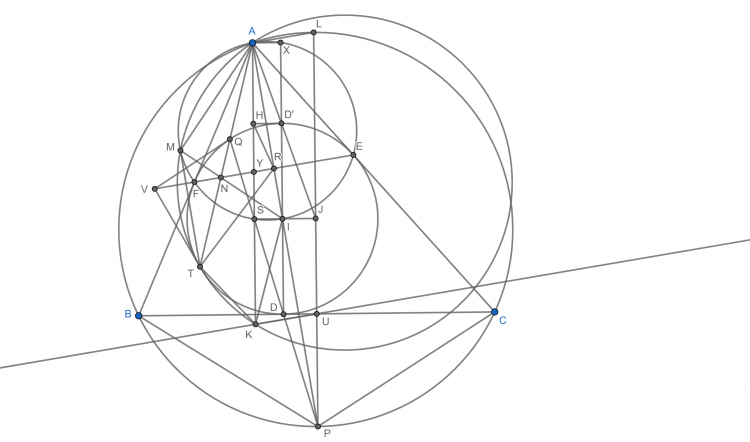
Bài 27. Cho tam giác $ABC$ nội tiếp $(O)$ và ngoại tiếp $(I)$ có $P$ là điểm chính giữa cung $BC$ nhỏ. $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. và $(AEF)$ cắt $(O)$ tại $Z$ khác $A$. $ZP$ cắt $(I)$ tại $Q$ và $AQ$ cắt $(I)$ tại $T$. $K$ là giao điểm của đường cao $AH$ và đường thẳng Simson của $P$ đối với tam giác $ABC$. Chứng minh $(ATK)$ tiếp xúc $(I)$
Gọi $R, U$ trung điểm $EF, BC$, $L$ là điểm chính giữa cung lớn $BC$ của $(O)$. $AQ$ cắt $EF$ tại $N$, $IN$ cắt $(AEF)$ tại $M$,
Xét phép nghịch đảo cực $I$, pt $=ID^2$, ta có được $(AMT)\leftrightarrow (RNT)$, $(I)\leftrightarrow (I)$
Kẻ tiếp tuyến tại $T$ của $(I)$ cắt $EF$ tại $V$. Vì $(QT, EF)=-1$ nên $VQ$ cũng là tiếp tuyến của $(I)$. Do đó $(VN, FE)=-1$ hay $VT^2=VF.VE=VN.VR$ (Maclaurin). Do đó $(RNT)$ tiếp xúc $(I)$ hay $(AMT)$ tiếp xúc $(I)$. Vì vậy ta cần chứng minh $K\in (AMT)$
Gọi $S$ là giao điểm của $PD$ với $AK$, $D'$ đối xứng với $D$ qua $(I)$, tiếp tuyến tại $D'$ của $(I)$ cắt $AK$ tại $H$. Ta sẽ chứng minh $H, R, I, K$ đồng viên.
Dễ thấy $S$ thuộc $(AEF)$ và $Q, H, D', I, S$ đồng viên
Ta có $ALUK$ là hình bình hành, $\Delta LUC\sim \Delta ARE\Rightarrow \frac{LC}{AE}=\frac{LU}{AR}=\frac{AK}{AR}$. Vì vậy ta cần chứng minh $\frac{AI}{AH}=\frac{LC}{AE}$ $(1)$
Dựng hình chữ nhật $AHD'X$, $AD'$ cắt $LU$ tại $J$, tính chất quen thuộc là $IJ//BC$ nên $IJUD$ là hình chữ nhật. Ta có $\frac{AD'}{XD'}=\frac{D'J}{ID'}$ $(2)$.
Ở đây $AH=XD'$ nên từ $(1)$ và $(2)$ thì ta cần chứng minh $\frac{AI}{AD'}=\frac{LC}{AE}.\frac{ID'}{D'J}\Leftrightarrow \frac{PI}{D'J}=\frac{LC}{AE}.\frac{ID'}{D'J}\Leftrightarrow \frac{PI}{LC}=\frac{ID}{AE}\Leftrightarrow \frac{PC}{LC}=\frac{IE}{AE}$ (hiển nhiên đúng)
Do đó ta có được $\frac{AK}{AR}=\frac{AI}{AH}$ hay $H, R, I, K$ đồng viên nên $AH.AK=AE^2$
Gọi $AK$ cắt $EF$ tại $Y$, xét phép nghịch đảo cực $A$ pt $= AE^2:$ $H\leftrightarrow K,I\leftrightarrow R,Q\leftrightarrow T,S\leftrightarrow Y$ mà $HIQS$ nội tiếp nên $YRKT$ nội tiếp
Để ý $T, M, Q, R, I$ đồng viên do đó $\widehat{TKA}=\widehat{TRY}=90^{\circ}-\widehat{TRI}=90^{\circ}-\widehat{TMI}=180^{\circ}-\widehat{AMT}$ hay $K\in (AMT)$. Do đó có đpcm.
- Diễn đàn Toán học
- → DaiphongLT nội dung



