Cho đa giác lồi $A_1A_2A_3\cdots A_{n-1}A_n.$ $M$ là một điểm bất kì nằm bên trong đa giác ($M$ không nằm trên cạnh của đa giác). Chứng minh rằng tồn tại $1$ trong các góc $\widehat{MA_1A_2},\widehat{MA_2A_3},\widehat{MA_3A_4},\cdots ,\widehat{MA_nA_1}$ có số đo không lớn hơn $\frac{90(n-2)}{n}^{\circ}$

Lời giải bài 23:

a) Ta có $\Delta CMB=\Delta AMD(c.g.c)\Rightarrow \widehat{MAD}=\widehat{MCB},\widehat{MDA}=\widehat{MBC}\Rightarrow$ tứ giác $AMPC,BMPD$ nội tiếp.

b) $\widehat{CMP}=\widehat{CAP}=\widehat{PDM}=\widehat{CBM}\Rightarrow \Delta CMP\sim \Delta CBM(g.g)\Rightarrow CP.CB=CM^2=AM^2\Rightarrow \sqrt{CP.CB}=AM.$ Tương tự cũng có $\sqrt{DP.DA}=MB\Rightarrow \text{đpcm}$

Lời giải bài 24:

a) $\widehat{ADE}=\widehat{AHE}=\widehat{ECB}\Rightarrow$ tứ giác $BDEC$ nội tiếp.

b) $\widehat{SHD}=\widehat{BAH}=\widehat{SEH}\Rightarrow SB.SC=SH^2(=SD.SE)$

c) Lấy $K$ đối xứng $H$ qua $S$ thì $SO//AK$ hay $SM//AK$ suy ra $\frac{BM}{MA}=\frac{BS}{SK}=\frac{BS}{SH}$
Mặt khác,  $SB.SC=SH^2\Rightarrow SB.HC=SH^2-SB.SH=SH.BH\Rightarrow \frac{BS}{SH}=\frac{BH}{HC}$ do đó $\frac{BM}{MA}=\frac{BH}{HC}\Rightarrow MH//AC$ hay $HP//EC.$ Từ đây suy ra tứ giác $BDPH$ nội tiếp $\Rightarrow BPH=\widehat{BDP}=90 ^{\circ}\Rightarrow BP \perp MH\Rightarrow BP \perp AC$

Cmtt, $CQ \perp AB$ suy ra đpcm.
 

Lời giải bài 25:

Dễ thấy $PQ$ đi qua trung điểm $K$ của $AB.$ Áp dụng định lí $Ceva$ cho tam giác $QAB$ có: $\frac{NA}{NQ}.\frac{KB}{KA}.\frac{MQ}{MB}=1\Rightarrow \frac{QN}{NA}=\frac{QM}{MB}\Rightarrow MN//AB.$ MÀ $PQ$ đi qua trung điểm của $AB$ do đó $PQ$ đi qua trung điểm của $MN.$ 

Bài 21: [Đề TS vào lớp 10 THPT Chuyên Ngoại Ngữ, Đại học Ngoại Ngữ, Đại học Quốc gia Hà Nội 2014 - 2015]

Cho tam giác ABC (AB < AC) nhọn nội tiếp (O). Kẻ đường cao AH. Gọi P, Q lần lượt là chân đường vuông góc kẻ từ H đến AB, AC.

a) Chứng minh: BCQP nội tiếp.

b) PQ kéo dài cắt BC tại M. Chứng minh : $MH^{2}=MB.MC$.

c) K là giao điểm của MA với đường tròn (O) (K khác A). I là tâm đường tròn ngoại tiếp tứ giác BCQP. Chứng minh rằng: I, H, K thẳng hàng.

Lời giải bài 21:

a) Ta có: $\widehat{APQ}=\widehat{AHQ}=\widehat{QCB}\Rightarrow \text{đpcm}$

b) $\widehat{MHP}=\widehat{BAH}=\widehat{MQH}\Rightarrow \Delta MHP\sim \Delta MQH\Rightarrow MH^2=MP.MQ$

c) $MH^2=MP.MQ=MB.MC=MK.MA\Rightarrow \Delta MHK\sim \Delta MAH\Rightarrow HK \perp AM(1)$

 Gọi $S,T$ lần lượt là trung điểm của $BQ,CP.$ Ta có: $MP.MQ=MK.MA$ nên tứ giác $KAQP$ nội tiếp $\Rightarrow \widehat{KPA}=\widehat{KQA}\Rightarrow \widehat{KPB}=\widehat{KQC}$ mà $\widehat{KBA}=\widehat{KCA}\Rightarrow \widehat{KBP}=\widehat{KCQ}$ suy ra $\Delta KBP\sim \Delta KCQ\Rightarrow \Delta KSP\sim \Delta KTQ\Rightarrow \widehat{KSP}=\widehat{KTQ}\Rightarrow \widehat{KSA}=\widehat{KTA}$ suy ra tứ giác $KATS$ nội tiếp mà tứ giác $SATI$ nội tiếp do đó $5$ điểm $K,A,T,I,S$ cùng thuộc $1$ đường tròn. Do đó $\widehat{IKA}=\widehat{ISA}=90^{\circ}\Rightarrow IK \perp AM(2)$

 Từ $(1),(2)$ suy ra $I,H,K$ thẳng hàng.

Bài 22 (Đề thi vào chuyên toán THPT chuyên Vĩnh Phúc 2013-2014):

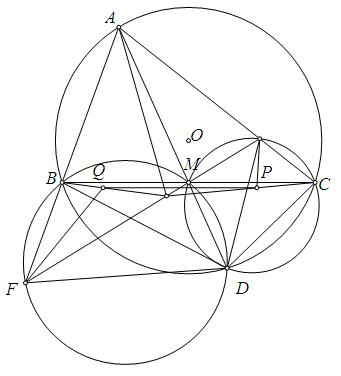
Cho tam giác $ABC$ nhọn $(AB<AC).$ Gọi $D,E,F$ lần lượt là chân các đường cao hạ từ $A,B,C.$ Gọi $P=BC\cap EF.$ Đường thẳng qua $D$ song song với $EF$ cắt $AB,AC,CF$ lần lượt tại $Q,R,S.$ Chứng minh rằng: 

 a) Tứ giác $BQCR$ nội tiếp.

 b) $D$ là trung điểm của $QS.$

 c) $(PQR)$ chia đôi $BC.$

Bài 20: [Đề vào 10 chuyên Lê Qúy Đôn Đà Nẵng 2016 - 2017]

Cho tam giác ABC có $\widehat{BAC}> 90^{0}$, AB < AC và nội tiếp đường tròn tâm O. Trung tuyến AM của tam giác ABC cắt (O) tại điểm thứ hai D. Tiếp tuyến của (O) tại D cắt đường thẳng BC tại S. Trên cung nhỏ DC của (O) lấy điểm E, đường thẳng SE cắt (O) tại điểm thứ hai là F. Gọi P, Q lần lượt là giao điểm của các đường thẳng AE, AF với BC

a) Chứng minh rằng MODS là tứ giác nội tiếp

b) Chứng minh rằng QB = PC

Lời giải bài 20:

a) Tứ giác $MDOS$ có $\angle OMS=\angle ODS=90^{\circ}\Rightarrow $ $MDOS$ là tứ giác nội tiếp.

b) Gọi $T=FM\cap (O),P'=TD\cap AE.$ Áp dụng định lý $Pascal$ cho bộ $\begin{pmatrix} DET \\ FDA \end{pmatrix}$ ta được $M,P',S$ thẳng hàng. Do đó $P\equiv P'$ hay $FM,DP$ cắt nhau trên $(O).$ 

 $AD,FT$ là $2$ dây cung đi qua trung điểm $M$ của dây cung $BC,$ $AF\cap BC=Q,TD\cap BC=P.$ Theo định lý con bướm ta có $MQ=MP$ suy ra $QB=PC.$

 

Bài 553: Giải hệ phương trình:

$\left\{\begin{matrix} &2x+\dfrac{1}{x+y}+\dfrac{1}{x-y}=\dfrac{16}{3} \\ &2(x^{2}+y^{2})+\dfrac{1}{(x+y)^{2}}+\dfrac{1}{(x-y)^{2}}=\dfrac{100}{9} \end{matrix}\right.$

 

Ta có:

$HPT\Leftrightarrow \left\{\begin{matrix} [(x-y)+\frac{1}{x-y}]+[(x+y)+\frac{1}{x+y}]=\frac{16}{3} \\ [(x-y)+\frac{1}{x-y}]^2+[(x+y)+\frac{1}{x+y}]^2=\frac{136}{9} \end{matrix}\right.\Leftrightarrow \begin{bmatrix} (x-y)+\frac{1}{x-y}=2;(x+y)+\frac{1}{x+y}=\frac{10}{3} \\ (x-y)+\frac{1}{x-y}=\frac{10}{3}; (x+y)+\frac{1}{x+y}=2 \end{bmatrix}\Leftrightarrow\begin{bmatrix} x=\frac{2}{3},y=-\frac{1}{3} \\ x=\frac{2}{3},y=\frac{1}{3} \\ x=\frac{2}{3},y=-1 \\ x=2,y=1 \end{bmatrix}$

Happy new year!

Cho tam giác $ABC$ nội tiếp $(O),$ ngoại tiếp $(I).$ Đường tròn $(I)$ tiếp xúc $BC$ tại $D.$ Lấy $M$ là điểm chính giữa cung $BC,$ $S$ đối xứng $A$ qua $(O).$ Chứng minh rằng $MD,SI$ cắt nhau tại $1$ điểm nằm trên $(O).$

Bài toán 4 : Tìm nghiệm nguyên của phương trình: $$x^2+y^2+z^2=x^2y^2$$

Bài toán 3 : Tìm tất cả nghiệm nguyên dương của phương trình 

$x^y+y^z+z^x=2(x+y+z)$

Giả sử cả $3$ số đều lớn hơn $1$ thì $x^y+y^z+z^x\geq x^2+y^2+z^2\geq \frac{(x+y+z)^2}{3}\geq 2(x+y+z)(\text{vì }x+y+z\geq 6).$ Dấu $"="$ xảy ra khi $x=y=z=2.$

 Xét trường hợp có $1$ số là $1$, giả sử $x=1$ thì $y^z=1+2y+z.$ Dễ thấy $y\geq 2.$ Ta sẽ chứng minh với $y,z\in \mathbb{Z}_+,y\geq 2$ thì $y^z>1+2y+z(1).$ Thật vậy, giả sử $(1)$ đúng với $z=k$ thì $y^k>1+2y+k.$ Với $z=k+1,(1)\Leftrightarrow y^{k+1}>2+2y+k(2)$

Ta có $VT(2)>y(1+2y+k)=2y^2+yk+y.$ Mà $2y^2+yk+y>2+2y+k\Leftrightarrow 2(2y-1)+k(y-1)>2, \text{đúng}.$

Vậy $\left ( x,y,z \right )=\left ( 2,2,2 \right )$ 

Bài toán 2 : Tìm mọi cặp số nguyên dương x , y sao cho $\frac{x^4+2}{x^2y+1}$ là số nguyên dương .

Ta có: $x^4+2\vdots x^2y+1\Rightarrow x^4y+2y\vdots x^2y+1\Rightarrow x^2(x^2y+1)+2y-x^2\vdots x^2y+1\Rightarrow x^2-2y\vdots x^2y+1.$ Xét $3$ trường hợp:

$+)TH1:x^2=2y\Rightarrow (x,y)=(2k^2,2k)(k\in \mathbb{Z}_+)$

$+)TH2:x^2>2y\Rightarrow x^2-2y\geq x^2y+1\Leftrightarrow (x^2+2)(y-1)\leq -3\Rightarrow y=1\Rightarrow x^4+2\vdots x^2+1\Rightarrow 3\vdots x^2+1(L)$

$+)TH3:x^2<2y\Rightarrow 2y-x^2\geq x^2y+1\Leftrightarrow (2-x^2)(y+1)\geq 3\Rightarrow x^2=1\Rightarrow x=1\Rightarrow y=2$

Vậy $\left ( x,y \right )\in \left \{ (1;2);(2k^2;2k) \right \}$

Lời giải bài 7:

1) Ta có: $\angle FBD=\angle ECD$ và $\angle BFD=\angle DMC=\angle DEC$ suy ra $\Delta BDF\sim \Delta CDE$

  Từ đó dễ dàng suy ra $\Delta DEF\sim \Delta DCB\Rightarrow \angle DFE=\angle DBC=\angle DFM\Rightarrow \overline{E,M,F}$

2) Kẻ tiếp tuyến $At$ của $(O)$ suy ra $\Rightarrow \angle tAB=\angle ADB=\angle AFE\Rightarrow AT//EF\Rightarrow EF \perp AO.$

3) 

$\frac{AC}{BD}=\frac{MC}{MD};\frac{AB}{DC}=\frac{MB}{MD}\Rightarrow \frac{AC}{BD}=\frac{AB}{DC}(MB=MC)\Rightarrow \frac{AC}{AB}=\frac{DB}{DC}(1)$

 Mặt khác ta lại có: $AE.AC=AB.AF(=AM.AD)\Rightarrow \frac{AC}{AB}=\frac{AF}{AE}(2)$

 Từ $(1)$ và $(2)$ suy ra $\frac{AF}{AE}=\frac{DB}{EC}\Rightarrow \frac{NF}{NE}=\frac{BF}{EC}\Rightarrow \frac{NF}{BF}=\frac{NE}{EC}\Rightarrow \frac{QN}{QB}=\frac{PN}{PC}$

 Theo định lí $Thales$ đảo suy ra $PQ//BC(\text{đpcm})$

Lời giải bài 8:

1) Ta có: $\angle GFA=\angle GEA \Rightarrow \angle GFB=\angle GEC.$ Mặt khác, $\angle GBF=\angle GCE$ suy ra $\Delta GBF\sim \Delta GCE\Rightarrow \Delta GNF\sim \Delta GME\Rightarrow \angle GNF=\angle GME\Rightarrow G\in (AMN)$

 Gọi $P'=AK\cap (K)\Rightarrow GP' \perp AG.$ Mà tứ giác $GHEA$ nội tiếp, $\angle AEH=90^{\circ}\Rightarrow GH \perp AG.$ Do đó $P'\in GH\Rightarrow P'\equiv P\Rightarrow \text{đpcm}$

Bài toán 9: Là Bài toán 6 em đề xuất ở trên rồi thầy.

Em xin đề xuất $2$ bài mới:

Bài toán 5 (Thi vòng 1 chuyên KHTN 2015-2016): Cho tam giác $ABC$ nhọn không cân có tâm đường tròn nội tiếp $I.$ $AI$ cắt $BC$ tại $D.$ Lấy $E,F$ lần lượt đối xứng $D$ qua $IB$ và $IC.$ $M,N,J$ lần lượt là trung điểm của $DE,DF,EF.$ Đường tròn ngoại tiếp tam giác $AEM$ cắt đường tròn ngoại tiếp tam giác $AFN$ tại $P$ khác $A.$ Chứng minh rằng $A,J,P$ thẳng hàng.

Bài toán 6 (Đề vòng 1 KHTN 2016-2017): Cho tam giác $ABC$ nội tiếp $(O)$ có A$AD$ là phân giác trong của tam giác. $AD$ cắt $(O)$ tại điểm thứ $2$ là $E.$ Gọi $M$ là trung điểm của $AD.$ $BM$ cắt $(O)$ tại điểm thứ hai $P$ khác $B.$ $EP$ cắt $AC$ tại điểm thứ hai $N.$

 a) Chứng minh $N$ là trung điểm của $AC.$

 b) Gọi $(EMN)$ cắt $BM$ tại $R$ khác $M.$ Chứng minh rằng $RA \perp RC.$

Câu 4: (6đ)

Cho tam giác ABC cân có $\measuredangle ABC=120$ nội tiếp (O). Tiếp tuyến qua A của (O) cắt đường thẳng BC tại D. Đường thẳng DO lần lượt cắt AB,AC tại E,F. Gọi M,N lần lượt là trung điểm của AB và AC. H là giao điểm của đường thẳng AO và (O). CMR:

b) AO, MF, NE đồng quy

Mượn tạm cái nình của anh Cuongpa

Từ phần $(a)$ dễ dàng suy ra được: $\frac{ME}{MA}=\frac{1}{3}$

Mặt khác, $\frac{HA}{HO}=2,$ và $\frac{FO}{FE}=\frac{AO}{AE}=\frac{AB}{AE}=\frac{3}{2}$

Do đó: $\frac{ME}{MA}.\frac{HA}{HO}.\frac{FO}{FE}=1.$ Áp dụng định lí $Menelaus$ cho $\Delta AEO$ ta được $M,F,H$ thẳng hàng. Suy ra đpcm.

$\boxed{10}.$ GHPT: $\left\{\begin{matrix} x^4+2x^3y-2x^2y^2-12xy^3+8y^4+1=0 \\ 2x^3y+y^4=1 \end{matrix}\right.$

$\boxed{11}.$ (Bài cuối cùng của phần HPT hữu tỉ)

 Giải HPT: $\left\{\begin{matrix} y^3-x^3=7 \\ x^3-y^2+x=-2 \end{matrix}\right.$

$\boxed{8}.$ Giải hệ phương trình:

$\left\{\begin{matrix}x^2(y-z)=\frac{-5}{3} \\ y^2(z-x)=3 \\ z^2(x-y)=\frac{1}{3}. \end{matrix}\right.$

$\boxed{8}.$ Đã có ở đây

$\boxed{9}.$ Giải hệ phương trình: $\left\{\begin{matrix} y^2+x(x+1)(x+2)(x+3)=121 \\ y^2+1=x \end{matrix}\right.$

$\boxed{7}.$ Giải hệ phương trình $\left\{\begin{matrix} x^4+5y=6 \;\;\;\ (1) \\ x^2y^2+5x=6 \end{matrix}\right.$

Trừ vế với vế $2$ phương trình được:

$(x-y)(x^3+x^2y-5)=0\Leftrightarrow \begin{bmatrix} x=y \\ x^3+x^2y=5 \end{bmatrix}$

$\bullet x=y\Rightarrow \begin{bmatrix} x=y=1 \\ x=y=-2 \end{bmatrix}$

$\bullet x^3+x^2y=5:$ Từ $(1)$ suy ra $y=\frac{6-x^4}{5}\Rightarrow x^3+\frac{6x^2-x^6}{5}=5\Leftrightarrow 5x^3+6x^2-x^6=25\Leftrightarrow 2x^6-10x^3-12x^2+50=0\Leftrightarrow (x^3-5)^2+[(x^6+8+8)-12x^2]+9=0, \text{phương trình vô nghiệm}$

Vậy $\boxed{(x,y)\in \left \{ (1;1);(-2;-2) \right \}}$

Anh đóng góp $1$ bài.

$\boxed{6}$ Giải hệ phương trình:

$\left\{\begin{matrix}4xy+4(x^2+y^2)+\frac{3}{(x+y)^2}=7 \\ 2x+\frac{1}{x+y}=3 \end{matrix}\right.$

 

P/S: Có bài nào hay anh sẽ tiếp tục đóng góp cho topic. 

Topic rất hay mong em tiếp tục phát triển. 

$\boxed{6}$ Ta có:

$HPT\Leftrightarrow \left\{\begin{matrix} 3(x+y)^2+(x-y)^2+\frac{3}{(x+y)^2}=7 \\ (x+y)+(x-y)+\frac{1}{x+y}=3 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3[(x+y)+\frac{1}{x+y}]^2+(x-y)^2=13 \\ [(x+y)+\frac{1}{x+y}]+(x-y)=3 \end{matrix}\right.$

 Đặt $x+y+\frac{1}{x+y}=a;x-y=b\Rightarrow \left\{\begin{matrix} 3a^2+b^2=13 \\ a+b=3 \end{matrix}\right.\Leftrightarrow \begin{bmatrix} a=2,b=1 \\ a=-\frac{1}{2},b=\frac{7}{2} \end{bmatrix}$

 Từ đó tìm được $\boxed{(x,y)=(1;0)}$

$\boxed{4}$ Giải hệ phương trình: $\left\{\begin{matrix} x+\frac{x+3y}{x^2+y^2}=3(1)\\ y-\frac{y-3x}{x^2+y^2}=0 (2)\end{matrix}\right.$

$\boxed{5}$ Giải hệ phương trình: $x^4-2y=y^4-2z=z^4-2x=\frac{-1}{2}$

$\boxed{4}:$ ĐKXĐ: $x,y$ không đồng thời bằng $0.$

$HPT\Rightarrow \left\{\begin{matrix} xy+\frac{xy+3y^2}{x^2+y^2}=3y \\ xy-\frac{xy-3x^2}{x^2+y^2}=0 \end{matrix}\right.\Rightarrow 2xy+3=2y\Rightarrow x=\frac{3y-3}{2y}$

Thay vào $(2)$ ta được:

$x^2y+y^3-y+3x=0\Leftrightarrow \frac{(3y-3)^2}{4y}+y^3-y+\frac{9y-9}{2y}=0\Rightarrow 4y^4+5y^2-9=0\Rightarrow y^2=1\Leftrightarrow \begin{bmatrix} y=1,x=0 \\ y=-1,x=3 \end{bmatrix}$

Vậy $\boxed{(x,y)\in \left \{ (0;1);(3;-1) \right \}}$

$\boxed{5}$

Dễ thấy $x,y,z>0.$

Trừ lần lượt phương trình thứ nhất và phương trình thứ hai, phương trình thứ hai và phương trình thứ ba ta được hệ mới:

$\left\{\begin{matrix} (x-y)(x+y)(x^2+y^2)+2(z-y)=0 \;\;\;\ (1) \\ (y-z)(y+z)(y^2+z^2)+2(x-z)=0 \;\;\;\ (2) \end{matrix}\right.$

Giả sử $x\geq y>0,$ từ $(1)$ suy ra $y\geq z$ suy ra $z\geq x$ (do $(2)$ ). Do đó $x\geq y\geq z\geq x>0\Leftrightarrow x=y=z$

Thay vào được $2x^4-4x+1=0$ (Sao nghiệm không đẹp nhỉ? )

$\boxed{2}$ Giải hệ phương trình: $\left\{\begin{matrix} x^3+y^3+x^2(y+z)=xyz+14\\ y^3+z^3+y^2(z+x)=xyz-21\\ z^3+x^3+z^2(x+y)=xyz+7 \end{matrix}\right.$

$\boxed{2}$

 

Cộng cả 3 pt ta có:
$2(x^3+y^3+z^3)+x^2(y+z)+y^2(z+x)+z^2(x+y)=3xyz$
$\Leftrightarrow (x^3+y^3+z^3-3xyz)+[x^3+x^2(y+z)]+[y^3+y^2(z+x)]+[z^3+z^2(x+y)]=0$
$\Leftrightarrow (x+y+z)(x^2+y^2+z^2-xy-yz-zx)+x^2(x+y+z)+y^2(x+y+z)+z^2(x+y+z)=0$
$\Leftrightarrow (x+y+z)(2x^2+2y^2+2z^2-xy-yz-zx)=0$
$\Rightarrow x+y+z=0$ (do $\Rightarrow 2x^2+2y^2+2z^2-xy-yz-zx> 0 \forall x,y,z$)

Tới đây rút gọn hệ được về dạng sau:
$\left\{\begin{matrix} y^3=xyz+14\\ z^3=xyz-21\\ x^3=xyz+7 \end{matrix}\right.$ (2)

Nhân cả 3 pt của (2) ta có:
$(xyz)^3=(xyz+14)(xyz-21)(xyz+7)$
$\Leftrightarrow (xyz)^3=(xyz)^3+(14-21+7)(xyz)^2+(14.7-14.21-7.21)xyz-7.14.21$$\Leftrightarrow 7^3xyz=-7^3.6$$\Leftrightarrow xyz=-6$

Thay vào (2) ta nhận được hệ pt:
$\left\{\begin{matrix} y^3=-6+14\\ z^3=-6-21\\ x^3=-6+7 \end{matrix}\right.$$\Leftrightarrow \left\{\begin{matrix} y^3=8\\ z^3=-27\\ x^3=1 \end{matrix}\right.$$\Leftrightarrow \left\{\begin{matrix} y=2\\ z=-3\\ x=1 \end{matrix}\right.$
Đây là nghiệm duy nhất của pt...

Ví dụ 1: Giải hệ phương trình: 

$\left\{\begin{matrix} 5x^3+3y^3=6+2xy\\ 3x^3+2y^3=8-3xy \end{matrix}\right.$

Từ $HPT$ suy ra: $\left\{\begin{matrix} x^3=13xy-12 \;\;\;\ (1) \\ y^3=-21xy+22 \;\;\;\ (2) \end{matrix}\right.$

Đặt $t=xy\Rightarrow t^3=(13t-12)(-21t+22)\Leftrightarrow t^3+273t^2-538t+24=0\Leftrightarrow (t-1)(t^2+274t-264)=0$

Tới đây tìm được các giá trị của $t$ hay chính là $xy$ từ đó thay vào $(1)$ và $(2)$ tìm được $x,y.$

Đáp số:

Bài 2: Cho $x,y,z>0$. Chứng minh rằng:

$\frac{\sqrt{x+y}}{z}+\frac{\sqrt{y+z}}{x}+\frac{\sqrt{z+x}}{y}\ge \frac{4x+4y+4z}{\sqrt{(x+y)(y+z)(z+x)}}$

Bất đẳng thức cần chứng minh tương đương với:

$$\sum [\frac{(x+y)\sqrt{(y+z)(z+x)}}{z}]\geq 4\sum x \;\;\;\;\ (1)$$

Thật vậy:

$$VT(1)\geq \sum \frac{(x+y)(z+\sqrt{xy})}{z}=2\sum x+\sum \frac{(x+y)\sqrt{xy}}{z}\geq 2\sum x+\sum \frac{2xy}{z}$$

Mà 

$$\sum \frac{2xy}{z}=\sum (\frac{xy}{z}+\frac{yz}{x})\geq \sum (2y)=2\sum x$$

Suy ra $(1)$ đúng.

Ta có đpcm. Dấu $"="$ xảy ra khi $x=y=z$

       Cho tam giác đều ABC nội tiếp đường tròn tâm O. Điểm E thay đổi trên cung nhỏ AB (E khác A và B). Từ B và C lần lượt kẻ các tiếp tuyến với đường tròn (O), các tiếp tuyến này cắt đường thẳng AE theo thứ tự tại M và N. Gọi F là giao điểm của BN và CM

            a) Chứng minh rằng $MB.CN=BC^{2}$

            b) Khi điểm E thay đổi trên cung nhỏ AB. Chứng minh rằng đường thẳng EF luôn đi qua một điểm cố định

(Trích đề thi TS vào THPT chuyên Toán Hà Tĩnh năm học 2016-2017)

a) Gọi độ dài cạnh tam giác đều là $a,$ ta có $AB//CN,AC//BM$ suy ra $\Delta AMB\sim \Delta NAC(g.g)\Rightarrow \frac{MB}{a}=\frac{a}{NC}\Rightarrow MB.CN=a^2=BC^2$

b) Từ $(a)$ suy ra $\frac{MB}{BC}=\frac{BC}{CN}$ mà $\widehat{MBC}=\widehat{NCB}(=120^{\circ})\Rightarrow \Delta MBC\sim \Delta BCN\Rightarrow \widehat{BMC}=\widehat{NBC}$ suy ra $\widehat{BFM}=\widehat{NBC}+\widehat{BCM}=\widehat{BMC}+\widehat{BCM}=180^{\circ}-\widehat{MBC}=60^{\circ}.$

 Mà $\widehat{BFM}=\widehat{ACB}=60^{\circ}\Rightarrow MEFB \;\;\ \text{ nội tiếp}\Rightarrow \widehat{BEF}=\widehat{BMC}=\widehat{NBC}$

 Gọi $P=EF\cap BC\Rightarrow \widehat{BEP}=\widehat{FBP}\Rightarrow \Delta EBP\sim \Delta BFP\Rightarrow BP^2=PE.PF$

 Chứng minh tương tự, có $CP^2=PE.PF$ suy ra $PB=PC.$

 Vậy $EF$ đi qua $P$ là trung điểm của $BC$ cố định.

Cho đa giác lồi: $A_1A_2...A_{100}.$ Tại mỗi đỉnh $A_k(k=\overline{1,100}),$ người ta ghi một số thực $a_k$ sao cho giá trị tuyệt đối của hiệu $2$ số trên $2$ đỉnh kề nhau chỉ bằng $2$ hoặc $3.$ Tìm GTLN có thể của giá trị tuyệt đối của hiệu giữa $2$ số ghi trên mỗi cặp đỉnh của đa giác đã cho, biết rằng các số ghi tại các đỉnh đã cho đôi một khác nhau.

Ta tiếp cận bằng 1 bài toán đơn giản sau: 

 

Bài toán:  Cho $a,b,c>0$. CMR:

 

$\frac{a(b+c)}{(b+c)^{2}+a^{2}}+\frac{b(c+a)}{(c+a)^{2}+b^{2}}+\frac{c(a+b)}{(a+b)^{2}+c^{2}}\leq \frac{6}{5}$

Do BĐT thuần nhất nên ta có thể chuẩn hóa $a+b+c=3.$

Khi đó:

$$\sum \frac{a(b+c)}{(b+c)^2+a^2}=\sum \frac{a(3-a)}{(3-a)^2+a^2}$$

Mặt khác ta có:

$$\frac{a(3-a)}{(3-a)^2+a^2}\leq \frac{9a+1}{25}\Leftrightarrow \frac{9(a-1)^2(2a+1)}{25\left [ a^2+(3-a)^2 \right ]}, \text{đúng }\forall a>0$$

Chứng minh tương tự suy ra:

$$\sum \frac{a(b+c)}{(b+c)^2+a^2}\leq \frac{9(a+b+c)+3}{25}=\frac{30}{25}=\frac{6}{5}.$$

Tìm các số nguyên dương $x,y$ sao cho:

$(x^2+y^2)^{2014}=(xy)^{2015}$.

Ta có: $(x^2+y^2)^{2014}=(xy)^{2015}\Leftrightarrow (\frac{x}{y}+\frac{y}{x})^{2014}=xy$

Do $xy\in \mathbb{N}^*$ và $\frac{x}{y}+\frac{y}{x}\in \mathbb{Q}$ suy ra $\frac{x}{y}+\frac{y}{x}\in \mathbb{N}^*(1).$

Đặt $d=\gcd(x,y)\Rightarrow x=dx_1;y=dy_1\left ( \text{với }(x_1,y_1)=1 \right )$

Suy ra $(1)\Leftrightarrow \frac{x_1}{y_1}+\frac{y_1}{x_1}\in \mathbb{N}*\Rightarrow x_1y_1|x_1^2+y_1^2.$ Do đó $x_1|y_1^2$ mà $\gcd(x_1,y_1)=1$ nên $x_1|y_1.$

Tương tự ta được $y_1|x_1.$ Do đó $x_1=y_1\Rightarrow x=y\Rightarrow 2^{2014}x^{4028}=x^{4030}\Leftrightarrow x^2=2^{2014}\Rightarrow x=2^{1007}$

Vậy  $x=y=2^{1007}$