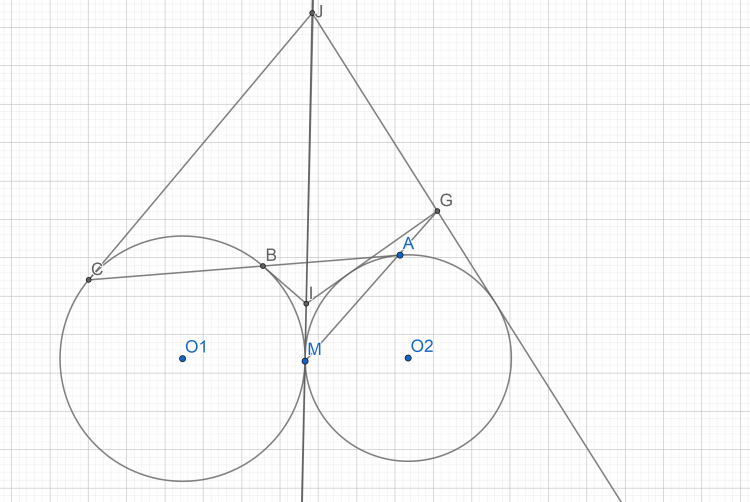
Cho hai đường tròn $(O1)$ và $(O2)$ tiếp xúc ngoài nhau tại $M.m$ là tiếp tuyến chung $(O_1),(O_2)$ tại $M.$ Từ điểm $A$ bất kỳ thuộc $(O_2)$ vẽ tiếp tuyến tại $A$ cắt $(O_1)$ tại $B,C.$ Các tiếp tuyến tại $B,C$ của $(O_1)$ cắt $m$ tại $I,J.$ Tiếp tuyến tại $I,J$ của $(O_2)$ cắt nhau tại $G.$

Chứng minh $AG$ đi qua một điểm cố định.

Cho tam giác $ABC$, điềm $P$ bất kỳ nằm trên đường trung trực của đoạn $BC$.Gọi $Q$ là điểm liên hợp đẳng giác của $P$. Giao của $(BPC)$ với $AB,AC$ lần lượt là $E,F$. Giao của $CE$ và $BF$ là H Chứng minh:  $P,H,Q$ thẳng hàng

Đường tròn $(I)$ nội tiếp tam giác $ABC$ tiếp xúc với $BC,CA,AB$ lần lượt tại $D,E,F$. $AD$ cắt $EF$ tại $J$. Một đường thẳng $d$ thay đổi qua $J$ cắt $(I)$ tại $M,N$($M$ và $C$ cùng phía so với $AD$), $DM$ cắt $AC,AB$ lần lượt tại $P,R$. $DN$ cắt $AB,AC$ lần lượt tại $Q,S$.
Chứng minh: $MN,PQ,RS$ đồng quy tại một điểm $T$ và khi $d$ thay đổi quanh $J$ thì $T$ luôn thuộc một đường thẳng cố định.

Ta có công thức góc chia đôi: $\frac{1-\cos\alpha}{2}=\sin^{2}\frac{\alpha}{2}$ suy ra $2\sin\frac{\alpha}{2}=\pm\sqrt{2-2\cos\alpha}$
(Trong đó dấu + hoặc - sẽ được chọn sao cho phù hợp với quy luật về dấu của hàm sin)
Ta chứng minh công thức
$2\sin(a_{1}+\frac{a_{1}a_{2}}{2}+\frac{a_{1}a_{2}a_{3}}{2^2}+...+\frac{a_{1}a_{2}...a_{n}}{2^{n-1}}).45^{\circ}$
$=\pm\sqrt{2+2\sin(a_{2}+\frac{a_{2}a_{3}}{2}+\frac{a_{2}a_{3}a_{4}}{2^2}+...+\frac{a_{2}a_{3}...a_{n}}{2^{n-2}}).45^{\circ}} (1)$

Nhận thấy:
+ Với $a_{1}=1$ thì:
$2\sin(a_{1}+\frac{a_{1}a_{2}}{2}+\frac{a_{1}a_{2}a_{3}}{2^2}+...+\frac{a_{1}a_{2}...a_{n}}{2^{n-1}}).45^{\circ}$ 

$=90^{\circ}+(a_{2}+\frac{a_{2}a_{3}}{2}+\frac{a_{2}a_{3}a_{4}}{2^2}+...+\frac{a_{2}a_{3}...a_{n}}{2^{n-2}}).45^{\circ}$
+ Với $a_{1}=-1$ thì:

$2\sin(a_{1}+\frac{a_{1}a_{2}}{2}+\frac{a_{1}a_{2}a_{3}}{2^2}+...+\frac{a_{1}a_{2}...a_{n}}{2^{n-1}}).45^{\circ}$ 

$=-[90^{\circ}+(a_{2}+\frac{a_{2}a_{3}}{2}+\frac{a_{2}a_{3}a_{4}}{2^2}+...+\frac{a_{2}a_{3}...a_{n}}{2^{n-2}}).45^{\circ}]$

Lại có:
$\cos\pm[90^{\circ}+(a_{2}+\frac{a_{2}a_{3}}{2}+\frac{a_{2}a_{3}a_{4}}{2^2}+...+\frac{a_{2}a_{3}...a_{n}}{2^{n-2}}).45^{\circ}]$
$=-\sin(a_{2}+\frac{a_{2}a_{3}}{2}+\frac{a_{2}a_{3}a_{4}}{2^2}+...+\frac{a_{2}a_{3}...a_{n}}{2^{n-2}}).45^{\circ}$

Áp dụng công thức góc chia đôi , ta chứng minh được công thức (1).

Để ý rằng các góc đang xét trên, nếu lấy giá trị tuyệt đối, thì chúng luôn nhỏ hơn $90^{\circ}$:
$(a_{1}+\frac{a_{1}a_{2}}{2}+\frac{a_{1}a_{2}a_{3}}{2^2}+...+\frac{a_{1}a_{2}...a_{n}}{2^{n-1}}).45^{\circ}$
$\leq (1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^n}).45^{\circ}=90^{\circ}-\frac{90^{\circ}}{2^{n+1}}<90^{\circ}$
Nên căn bậc hai trong công thức trên sẽ có dấu + hoặc - phụ thuộc vào dấu của $a_{1}$, nên ta có thể viết lại thành:
$2\sin(a_{1}+\frac{a_{1}a_{2}}{2}+\frac{a_{1}a_{2}a_{3}}{2^2}+...+\frac{a_{1}a_{2}...a_{n}}{2^{n-1}}).45^{\circ}$
$=a_{1}\sqrt{2+2\sin(a_{2}+\frac{a_{2}a_{3}}{2}+\frac{a_{2}a_{3}a_{4}}{2^2}+...+\frac{a_{2}a_{3}...a_{n}}{2^{n-2}}).45^{\circ}}$

Vì các $a_{i}$ chỉ nhận giá trị là $1$ và $-1$ nên ta dễ thấy $2sina_{i}.45^{\circ}=a_{i}\sqrt{2}$
từ đó áp dụng liên tiếp công thức (1) , ta suy ra được hệ thức sau :
$2\sin(a_{1}+\frac{a_{1}a_{2}}{2}+\frac{a_{1}a_{2}a_{3}}{2^2}+...+\frac{a_{1}a_{2}...a_{n}}{2^{n-1}}).45^{\circ}$
$=a_{1}\sqrt{2+2\sin(a_{2}+\frac{a_{2}a_{3}}{2}+\frac{a_{2}a_{3}a_{4}}{2^2}+...+\frac{a_{2}a_{3}...a_{n}}{2^{n-2}}).45^{\circ}}$

$=a_1\sqrt{2+a_2\sqrt{2+2\sin(a_{3}+\frac{a_{3}a_{4}}{2}+\frac{a_{3}a_{4}a_{5}}{2^2}+...+\frac{a_{3}a_{4}...a_{n}}{2^{n-3}}).45^{\circ}}}$

$=....=a_{1}\sqrt{2+a_{2}\sqrt{2+a_{3}\sqrt{2+....+a_{n}\sqrt{2}}}}$ (đpcm)

Câu 1: Tìm tất cả các giá trị m thực để dãy: $\left\{\begin{matrix} x_{1}=\sqrt{2018}\\ x_{2}=\frac{m}{x_{n}^2+1} \end{matrix}\right.$ có giới hạn hữu hạn
Câu 2: Chứng minh dãy $\left\{\begin{matrix} x_{1}=1\\x_{n+1}=1+\frac{2018}{x_{n}+1} \end{matrix}\right.$ có giới hạn hữu hạn. Tìm giới hạn đó

Screen Shot 2017-12-16 at 12.09.52 PM.png

a) $L,P$ là trung điểm $AB,AC.$ Theo định lí bốn điểm,

$(MO^2-NO^2)-(MI^2-NI^2)=(MP^2+PO^2-NL^2-LO^2)-(BI^2-CI^2)= \frac{(MC-MA)^2-(NB-NA)^2+BA^2-CA^2}{4}-(BD^2-CD^2)$

$= \frac{(2BC-AC)^2-(2BC-AB)^2+BA^2-CA^2}{4}-(BD^2-CD^2)= \frac{(2BC-2AC)2BC-(2BC-2AB)2BC}{4}-BC(BD-CD)$

$=(BC-AC)BC-(BC-AB)BC-BC(BD-CD)=BC(BC-AC-BC+AB-BD+CD)=0 \Rightarrow$ đpcm.

b) $H=(AMN) \cap (ABC), H \neq A.$

$\widehat{HNB}=180^0- \widehat{HNA}=180^0- \widehat{HMA}= \widehat{HMC}, \widehat{HBN}= \widehat{HCN}$

$\Rightarrow \Delta HNB \sim \Delta HNC.$ Mà $NB=BC=CM \Rightarrow \Delta HNB= \Delta HMC$

$\Rightarrow HB=HC,HM=HN \Rightarrow HX \perp MN,HO \perp BC.$

Theo định lí bốn điểm, $BX^2-CX^2=(BX^2-R_X^2)-(CX^2-R_X^2)=BN.BA-CM.CA=BC(BA-AC)=BC(BD-DC)=BD^2-CD^2$

$\Rightarrow XD \perp BC \Rightarrow HX \parallel OI,HO \parallel IX \Rightarrow OI=HX=R_X.$ (đpcm)

c) $HB=HC \Rightarrow HA \perp AI \Rightarrow AI \parallel XO.$ 

Ta có $AX=OI$ nên $AXOI$ là hình bình hành hoặc hình thang cân.

Nếu $AXOI$ là hình bình hành thì $A \equiv H \Rightarrow AB=AC$ vô lí, nên $AXOI$ là hình thang cân $\Rightarrow A,X,O,I$ đồng viên. (đpcm)

Bài này đã có lời giải ở đây https://diendantoanh...tâm-nội-tiếp-i/

Cho tam giác $ABC$ có tâm nội tiếp $I$, tâm ngoại tiếp $O$. $M,N$ lần lượt là hai điểm đối xứng của $B,C$ tương ứng qua $IB,IC$. Gọi $X$ là tâm ngoại tiếp tam giác $AMN$. Khi đó:

a) $MN \perp OI$

b) Bán kính đường trong ngoại tiếp tam giác $AMN$ bằng $OI$

c) $A,X,I,O$ đồng viên

Cách 2: Trên trục tọa độ gọi vị trí $A(a),B(b),C(c),M(x)$ 
BDT viết lại thành 
$\left | \frac{(x-a)(x-b)}{(c-a)(c-b)} \right |+\left | \frac{(x-b)(x-c)}{(a-b)(a-c)} \right |+\left | \frac{(x-c)(x-a)}{(b-c)(c-a)} \right | \geq 1$
Ta có:
$ VT \geq \left | \frac{(x-a)(x-b)}{(c-a)(c-b)}+\frac{(x-b)(x-c)}{(a-b)(a-c)}+ \frac{(x-c)(x-a)}{(b-c)(c-a)} \right |$
Mà để ý thấy $f(x)-1= \frac{(x-a)(x-b)}{(c-a)(c-b)}+\frac{(x-b)(x-c)}{(a-b)(a-c)}+ \frac{(x-c)(x-a)}{(b-c)(c-a)}-1$ có bậc cao nhất là bậc $2$
Nhưng lại có 3 nghiệm phân biệt $f(a)-1=f(b)-1=f(c)-1=0$ suy ra $f(x)\equiv 1$ suy ra $đpcm$

Gọi $I$ là tâm tỉ cự của ba điểm $(A,B,C)$ bộ số $(x,y,z)$ , áp dụng công thức Jacobi ta được:

$xMA^2+yMB^2+zMC^2=(x+y+z)MI^2+\frac{xy.c^2+yz.a^2+zx.b^2}{x+y+z} \geq \frac{xy.c^2+yz.a^2+zx.b^2}{x+y+z}$

Chọn $x=\frac{a}{MA},y=\frac{b}{MB},x=\frac{c}{MC}$ suy ra 
$aMA+bMB+cMC \geq \frac{abc(aMA+bMB+cMC)}{a.MB.MC+b.MC.MA+c.MA.MB}$ suy ra $đpcm$

Cho ba số thực $a,b,c$ thay đổi . Tìm giá trị lớn nhất của biểu thức:
$P=3\sqrt[3]{\frac{c^2-3a^2}{6}}-2\sqrt{\frac{a^2+b^2+c^2-ab-bc-ca}{3}}$

Cho tam giác ABC có a=BC, b=CA, c=AB, $min{A,B,C} \geq 15^{\circ}$. Chứng minh $\sqrt{ab}, \sqrt{bc}, \sqrt{ca}$ cũng là độ dài ba cạnh của một tam giác.

Vậy bài này thì mình gán bít 0 và 1 ntn ạ?

(Bạn tự vẽ hình nhé)
Gọi $I=AM \cap B'D'$. Dễ thấy $S,O,I$ thẳng hàng( nằm trên giao tuyến của $(SAC)$ và $(SBD)$) và I là trọng tâm mặt $(SAC)$

Đặt $x=\frac{SB}{SB'},y=\frac{SC}{SC'}$.
Dễ chứng minh $x+y=2\frac{SO}{SI}=3$ (chứng minh bằng cách kẻ đường song song qua B cắt SO tại K và dùng định lý Thales suy ra tỷ số)
Từ đó ta cũng suy ra $x,y\in[1;2]$
Ta có $\frac{1}{x}+\frac{1}{y} \geq \frac{4}{x+y} \geq \frac{4}{3}$
$\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}=\frac{3}{xy}\leq\frac{3}{2}$
 

Có bao nhiêu cách chọn từ 2018 số nguyên dương đầu tiên ra 1000 số nguyên đôi một khác nhau sao cho không có hai số nào là hai số nguyên liên tiếp?

Tìm cặp số nguyên dương (x,y)với x,y nguyên tố cùng nhau và thỏa mãn phương trình $2(x^{3}-x)=y^{3}-y$

Topic hơi vắng Tổ hợp nhỉ:  
Bài 37:  (Mathematical Excaibur Vol.7, No.5): Hai mươi người cùng ngồi xung quanh một cái bàn và chơi một trò chơi với $n$ quân bài . Ban đầu một người giữ tất cả quân bài. Đến lượt mỗi người, nếu có ít nhất một người giữ ít nhất 2 quân bài, một trong số họ sẽ phải chuyển một quân bài cho mỗi người ngồi bên cạnh mình. Trò chơi kết thúc khi và chỉ khi mỗi người giữ nhiều nhất một quân bài.
a. chứng minh rằng nếu $n\geq 20$ thì trò chơi không thể kết thúc.
b. chứng minh rằng nếu $n<20$ thì trò chơi sẽ phải kết thúc.

Tìm số hạng tổng quát của dãy số $\left\{\begin{matrix} y_{1}=7\\y_{n+1}=y_{n}^{4}-8y_{n}^{2}+1 ,\forall n=1,2 \end{matrix}\right.$

$a\sqrt{a}(x-2)^{2}+\frac{\sqrt{a}}{(x-2)^{2}}\leq \sqrt[4]{a}\left | cos\frac{x\pi}{2} \right |$

 

Sau đây mình xin gửi đến các tài liệu mà mình có. Các tài liệu này mình đã chọn riêng ra và nhìn chung phù hợp với đa số các bạn. 

Hi vọng các bạn đóng góp thêm các tài liệu hay để chúng ta có thể học tập hiệu quả.

 

Bất đẳng thức: http://www.mediafire...2gy6rgmo9ldi6zi

Dãy số: http://www.mediafire...i4m7rypjd9m5i8t

Giải tích: http://www.mediafire...dfmxcjmf93hlsdz

Hình học: http://www.mediafire...kwt5aa55c4w1tl5

Phươpng trình hàm: http://www.mediafire...e5cwc6704lcjwyd

Số học: http://www.mediafire...945dknp60hdafv2

Tài liệu ôn thi vào lớp 10 THPT http://www.mediafire...sb87c32uibp6ct9

 

Một số tài liệu khác:

http://www.mediafire...5b1fszbwgcgz15t

http://www.mediafire...ctsgkor91569jqx

http://www.mediafire...mo5zj0ko88f1pg8

http://www.mediafire...62mgxrrcug4ivug

http://www.mediafire...lmp45uznc69nkg2

http://www.mediafire...l3fng3qf93gl0x2 (toán cao cấp)

 

Anh/chị zipienie gì đó cho em xin lại link với! Link die hết rồi ạ. 

Bài 28: Ta có $f(d)-d=f_{2018}(d)-f_{2017}(d)=f(f_{2017}(d))-f(f_{2016}(d)) \vdots f_{2017}(d)-f_{2016}(d),$
$f_{2017}(d)-f_{2016}(d) = f(f_{2016}(d))-f(f_{2015}(d)) \vdots f_{2016}(d)-f_{2015}(d),$
Thực hiện tương tự, ta được :
$f_{2}(d)-f_{1}(d) = f(f(d))-f(d) \vdots f(d)-d.$

Từ đó, $\left | f(d)-d \right |=\left | f_{2}(d)-f(d) \right |=...=\left | f_{2017}(d)-f_{2016}(d) \right |$

Vì $0=f_{2017}(d)-d=\left\{\begin{matrix} k \\ 2017k \end{matrix}\right.$ nên k=0 suy ra $f(d)=d$

Bài 29:

Với $k \leq 2016$ giả sử tồn tại hai dãy $(a_{i})$ và $(b_{i})$ thỏa mãn đề bài. 
Khi đó do $a_{1} \neq b_{1}$ nên KMTTQ có thể giả sử $a_{1} < b_{1}$.
Từ điều kiện (a), tồn tại các số nguyên $0 \leq m < n$ sao cho: $a_{1}=2016^m,  b_{1}=2016^n$

Do  $b_{i} \geq  b_{1}$ với mọi $i$ nên tổng $\sum _{i=1}^{k}b_{i} \vdots 2016^n$
Gọi $l$ là số các chỉ số i sao cho $a_{i} =  a_{1} = 2016^m$, khi đó 
$\sum _{i=1}^{k}a_{i} \vdots 2016^n \equiv l.2016^m \equiv 0 (mod2016^n)$ 
Vì $n \geq m+1$ nên $l \vdots 2016$, suy ra $k \geq l \geq 2016$
Vậy ta phải có $k=l=2016$. Từ đó suy ra 

$\sum _{i=1}^{k}a_{i} = \sum _{i=1}^{2016}a_{i}  = 2016^{m+1}= \sum _{i=1}^{2016}b_{i} > 2016.b_{1}=2016^{n+1} > 2016^{m+1}$ (vô lý)

Suy ra dpcm

Bài 28[sáng tác] Cho $a,b,c,d$ là các số nguyên a khác 0. Giả sử đa thức$f(x)=ax^2+bx+c$ thỏa mãn $f_{2017}(d)=d$. Chứng minh $f(d)=d$

Bài 29[phỏng theo Korea 1997] Chứng minh rằng với $k \geq 2017, k \in Z$, luôn tồn tại hai dãy số $(a_{i})_{i=1}^{k}$ và $(b_{i})_{i=1}^{k}$ thỏa mãn 
(a) $a_{i}, b_{i}$ $\in$ ${1,2016,2016^2,...,}$ với $i=1,2,..,k$

(b) $a_{i} \neq b_{i}$ với $i=1,2,..,k$

(c) $a_{i} \leq a_{i+1}$ và  $b_{i} \leq b_{i+1}$ với $i=1,2,..,k-1$

(d) $\Sigma_{i=1}^{k}a_{i}=\Sigma_{i=1}^{k}b_{i}$

Bài 18 [Sưu tầm]: Cho $0<a<b<c$ thỏa mãn $a+b+c=6$ và $ab+bc+ca=9$. Chứng minh rằng: $0<a<1<b<3<c<4$

Bài 19 [Sưu tầm]: Tồn tại hay không một hàm $f$ : $N$ → $N$ sao cho $f(f(n-1))=f(n-1)-f(n)$ ,∀ $n$ ≥ $2$?

Cho $a,b,c$ là 3 số nguyên dương. Chứng minh rằng $a^2+b^2+c^2$ không chia hết cho $3(ab+ac+bc).$

$sinA+sinB+sinC=1+cosA+cosB+cosC$

$\Leftrightarrow$ $2sin\frac{A+B}{2}cos\frac{A-B}{2}+2sin\frac{C}{2}cos\frac{C}{2}=2cos\frac{A+B}{2}cos\frac{A-B}{2}+2cos^2\frac{C}{2}$

$\Leftrightarrow$ $cos\frac{C}{2}cos\frac{A-B}{2}+sin\frac{C}{2}cos\frac{C}{2}=sin\frac{C}{2}cos\frac{A-B}{2}+cos^2\frac{C}{2}$

$\Leftrightarrow$ $cos\frac{A-B}{2}(cos\frac{C}{2}-sin\frac{C}{2})-cos\frac{C}{2}(cos\frac{C}{2}-sin\frac{C}{2})=0$

$\Leftrightarrow$ $(cos\frac{C}{2}-sin\frac{C}{2})(cos\frac{A-B}{2}-cos\frac{C}{2})=0$

$\Leftrightarrow$ $sin\frac{A-B+C}{4}sin\frac{A-B-C}{4}cos(\frac{C}{2}+\frac{\pi }{4})=0$

Đến đây bạn dễ dàng suy ra được rồi bạn. =))

I.2 

Ta có: $f(x).f(x+1)=f(x)[(x+1)^2+p(x+1)+q]$
$=f(x)[(x^2+px+q)+2x+1+p]$ 

$=f(x)[f(x)+2x+1+p]$
$=f^2(x)+2.f(x).x+f(x)+p.f(x)$

$=f^2(x)+2.f(x).x+x^2+px+q+p.f(x)$

$=[f(x)+x]^2+p[f(x)+x]+q=f(f(x)+x)$

Với $x=20167$, ta chọn $k=f(2016)+2016$ thì được đpcm.