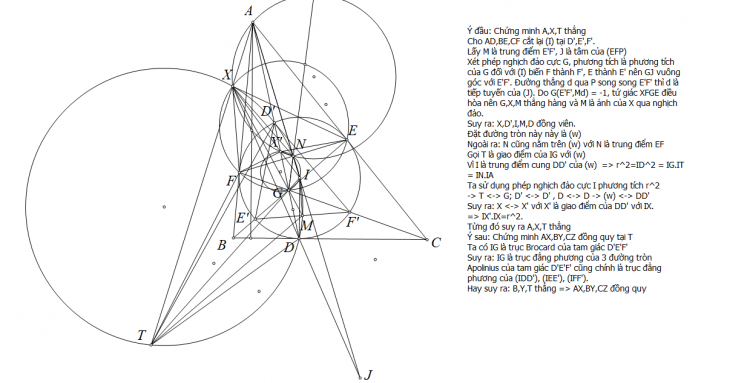
Bài toán 2. Cho tam giác $\displaystyle ABC$ có trực tâm $\displaystyle H$ và $\displaystyle D,E,F$ lần lượt là hình chiếu của $\displaystyle A,B,C$ xuống $\displaystyle BC,CA,AB$. Gọi $\displaystyle L$ là điểm Lemoine của $\displaystyle ABC$ và $\displaystyle O$ là tâm ngoại tiếp của $\displaystyle ABC$. Chứng minh $\displaystyle OL$ đi qua trực tâm $\displaystyle DEF$.

 

Đây là lời giải bài 2 bằng tọa độ số phức : )

Lời giải Bài toán 1. 

 

Bài này còn 1 cách nữa dùng Desargues cho KBC và AMN nhưng rất trâu và dài không kém cách này. có thời gian mình sẽ đăng sau

Ở đoạn bạn biến đổi tỉ số kép bằng sin, hình như bạn đã viết sai và theo mình đó là: $ \boxed{C(QNOA) = \frac{\sin\angle OCA}{\sin\angle QCA}.\frac{\sin\angle NCD}{\sin \angle NCA}}$

Bài toán 3. Cho tam giác $\displaystyle ABC$ ngoại tiếp $\displaystyle ( I)$ và tiếp xúc $\displaystyle BC,CA,AB$ tại $\displaystyle D,E,F$. $\displaystyle G$ là điểm Gergonne của tam giác $\displaystyle ABC$. Dựng $\displaystyle X$ sao cho $\displaystyle GEXF$ là tứ giác điều hòa. Định nghĩa tương tự $\displaystyle Y,Z$. Chứng minh $\displaystyle AX,BY,CZ$ đồng quy.

Khó thật đấy, mình giải hơn 2 ngày

• Vòng 1: 

$\text{Bài } 1:(4\textit{ điểm)}$ Giải hệ phương trình: 

$$\begin{array}{l} x^3-y-1=\sqrt[3]{x^3+y+1}\\ y+4=x+2\sqrt{x} \end{array}$$

$\text{Bài } 2:(4\textit{ điểm)}$ Cho tam giác $ABC$ nộp tiếp đường tròn $(O)$ có đường tròn nội tiếp $(I)$ tiếp xúc với $BC, CA, AB$ tại $D, E, F$. Gọi $X, Y$ lần lượt là giao điểm của $AI$ với $DF, DE$. Đường tròn đường kính $XY$ cắt $BC$ tại $S, T$ với $S$ nằm giữa $B, T$. 

           a) Chứng minh $SX$ là phân giác trong của góc $AST$

           b) Chứng minh $(AST)$ tiếp xúc với $(O)$ 

$\text{Bài } 3:(4\textit{ điểm)}$ Tìm tất cả các số tự nhiên sao cho $\frac{(n+1)^{3n+1}-3n-2}{3n+1}$ là số nguyên.

$\text{Bài } 4:(4\textit{ điểm)}$ Tìm tất cả các hàm $f:\mathbb{Q} \to \mathbb{Q}$ sao cho 

$$f(10f(x)+f(y))=10x+y$$ với mọi $x,y$ thuộc $\mathbb{Q}$.

$\text{Bài } 5:(4\textit{ điểm)}$ Xét $A$ là tập con của $S = \{1;2;\dots;2010\}$ sao cho tổng hai phần tử (phân biệt) tùy ý của $A$ không là bội của $125$.

           a) Cho ví dụ một tập hợp $A$ có đúng $1003$ phẩn tử.

           b) Tập $A$ có nhiều nhất bao nhiêu phần tử?  

• Vòng 2: 

$\text{Bài } 1:(5\textit{ điểm)}$

                Cho $a, b, c>0$ thỏa mãn $abc=1$. Chứng minh bất đẳng thức sau: 

$$\frac{1}{a}+\frac{1}{b} +\frac{1}{c}+\frac{6}{a+b+c} \geq 5$$ 

$\text{Bài } 2:(6\textit{ điểm)}$

                Cho tam giác $ABC \textit{(AB<AC)}$ nhọn nôi tiếp đường tròn $(O)$, trực tâm $H$, $G$ là trọng tâm và $D$ là chân đường cao của $A$ lên $BC$. Đường tròn $(BOC)\textit{(có đường kính $OO'$)}$ lần lượt cắt $AC$ và tia đối tia $BA$ tại $E,F$. Các tia $EO,FO$ cắt $(O)$ tại $E',F'\textit{(E',F' nằm cùng phía nhau bờ BC)}$. $BF',CE'$ cắt nhau tại $I$, chân đường vuông góc của $I$ lên $BC$ là $R$. $AI$ cắt lại $(O)$ tại $X, XR$ cắt lại đường tròn $(O)$ tại $P$. 

           a) Tia $PI$ cắt lại đường tròn $(O)$ tại $Y$. Gọi $T$ là tâm đường tròn $A-Apollonius$ của tam giác $ABC, OT$ cắt $AD$ tại $K, YK$ cắt $BC$ tại $Z$. Gọi $L$ là hình chiếu của $O$ lên $AZ$. Chứng minh rằng đường tròn $(DLZ)$ tiếp xúc với đường tròn $(BOC)$. 

           b) Tia $O'D$ cắt $(O)$ tại $D_1,D_2 \textit{($D_2$ thuộc đoạn O'D)}$. $D_1H$ cắt $D_2G$ tại $G_1$ và $D_2H$ cắt $D_1G$ tại $G_2$. Gọi $M$ là trung điểm $BC$, $J$ là trung điểm $DM, G_1G_2$ cắt lại đường tròn $(G_1JR)$ tại $W$. Đường thẳng $WR$ cắt $G_2D, G_2M$ theo thứ tự tại $W_1, W_2.$ Chứng minh rằng $W$ là trung điểm của đoạn $W_1,W_2.$

$\text{Bài } 3:(5\textit{ điểm)}$

                Tìm tất cả các hàm số $f:\mathbb{N} \to \mathbb{N}$ thỏa mãn các điều kiện sau: 

           i)       $0 \leq f(m) \leq m^2; \forall m \in \mathbb N$

           ii)      $f(m)-f(n)$ chia hết cho $m-n; \forall m,n \in \mathbb N, m > n$

($N$ là tập số tự nhiên)

$\text{Bài } 4:(4\textit{ điểm)}$

                Chứng minh rằng $\binom{2n}{n} \mid \textit{lcm}(1,2,\dots,2n)$ với mọi số nguyên dương $n$; trong đó $\binom{m}{k}$ là tổ hợp chập $k$ của $m$ phần tử và $\textit{lcm}(a,b)$ là bội chung nhỏ nhất của $a$ và $b$. 
                                                                                   __________________Hết__________________

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ có đường tròn nội tiếp $(I)$ tiếp xúc với $BC, CA, AB$ tại $D, E, F$. Gọi $X, Y$ lần lượt là giao điểm của $AI$ với $DE, DF$. Đường tròn đường kính $XY$ cắt $BC$ lần lượt tại $S, T$. Chứng minh rằng $(AST)$ tiếp xúc $(I)$

Cho $\Delta ABC$ ngoại tiếp $(I)$, $(I)$ tiếp xúc với $BC$, $CA$, $AB$ tại $D$, $E$, $F$. Dựng hình bình hành $ABPC$, đường thẳng qua $P$ vuông góc với $EF$ tại $K$. Chứng minh $DK$, $DP$ đẳng giác $\widehat{EDF}$
P/s:   

Không biết có phải trùng hợp không chứ câu này đang nằm trong số tháng 9 của tạp chí Pi 
Mình nghĩ là bạn không nên đăng ở diễn đàn
Nếu không phải thì cho mình xin lỗi nha. 

$\boxed{29}$ Cho $\Delta ABC$ cân tại $A$ nội tiếp $(O)$, $D$ thuộc $BC$ và dựng hình bình hành $AEDF$ ($E$, $F$ thuộc $AC$, $AB$). $G$ đối xứng với $D$ qua $EF$. $DE$ cắt $(AEF)$ tại $H$ . $K$ thuộc $(O)$ sao cho $\widehat{KGH}=90^{\circ}$ , $L$ thuộc $(AEF)$ sao cho $\widehat{LGC}=90^{\circ}$. Gọi $P$, $Q$ lần lượt là tâm $(GKD)$, $(GLD)$. Chứng minh $AGQP$ nội tiếp
P/s: bài này hay

ủa sao mình vẽ không được nhỉ 

Dưới đây là 2 bài khai thác điểm Fermat: 

$\boxed{27}$: Cho tam giác $ABC$ có điểm $F$ là điểm Fermat. $AF,BF,CF$ cắt $BC,CA,AB$ tại $X,Y,Z$. Chứng minh đường tròn ngoại tiếp tam giác $XYZ$ tiếp xúc với đường tròn Euler của tam giác $ABC$.

$\boxed{28}$: Cho tam giác $ABC$ nội tiếp có điểm $F$ là điểm Fermat. $AF,BF,CF$ cắt $(O)$ tại $X,Y,Z$. Gọi $H_1,H_2$ là các trực tâm của tam giác $ABC$ và $XYZ$. Chứng minh $F$ là trọng tâm của tam giác $H_1H_2O$. 

$\boxed{26}$: Gọi $I, K$ là tâm đường tròn nội tiếp lần lượt của 2 tam giác $ABC$ và $DBC$. Chứng minh độ dài $IK$ không vượt quá $AD$

$D$ là gì nhỉ bạn?

Giả sử $(O)$ là $(ABC)$.

$(OPP')$ cắt lại $(O)$ tại $F$.

Ta có $\angle FOG=\angle FPG=\frac{\angle FOA}{2}$ nên OG là phân giác của $\angle FOA$.

Suy ra A, F đối xứng với nhau qua OG.

Gọi E là trực tâm $\Delta AGO$ thì A, E, F thẳng hàng.

Gọi $D$ là điểm đối xứng với H qua BC.

Ta có $(P'O,P'E)\equiv (GO,GE)\equiv (AE,AO)\equiv \frac{\pi}{2}+(GO,AO)\equiv \frac{\pi}{2}+(GO,GA)+(AG,AO)\equiv \frac{\pi}{2}+(P'O,P'P)+(AP,AO)\equiv (P'O,BC)+\frac{\pi}{2}+\frac{(OP,OA)}{2}\equiv (P'O,BC)+\frac{\pi}{2}+(DP,DA)\equiv (P'O,BC)+(DP,BC)\equiv (P'O,BC)+(BC,HP')\equiv (P'O,HP')(\mod\pi)$.

Vậy E, H, P' thẳng hàng.

Hay! Anh cũng dùng góc mà quên mất có nhiều trường hợp hình 

$\boxed{25}$: Cho tam giác $ABC$ có trực tâm $H$. $P$ là một điểm bất kì nằm trên cung $BC$ không chứa $A$. Gọi $P'$ là điểm đối xứng của $P$ qua $BC$. Đường tròn ngoại tiếp $\triangle OPP'$ cắt $AP$ tại $G$. Chứng minh trực tâm của tam giác $AGO$ nằm trên $HP'$.  

$\boxed{24}$: Cho $\triangle ABC$ và $M$ là một điểm nằm trong đường tròn ngoại tiếp $\triangle ABC$.

a/ Chứng minh rằng $AM.BC,BM.AC,CM.AB$ là độ dài 3 cạnh của 1 tam giác $\triangle$.

b/ Tìm vị trí điểm $M$ sao cho điện tích tam giác $\triangle$ là lớn nhất.
 

Cho tam giác nhọn ABC với đường tròn nội tiếp (I). Gọi ($O_{a}$) là đường tròn có tâm nằm trên đường cao kẻ từ A, đi qua A và tiếp xúc trong với đường tròn (I) tại $A_{1}$, các điểm $B_{1}$, $C_{1}$ được xác định tương tự.

a) CMR AA1, BB1, CC1 đồng quy tại P.

b) Gọi ($J_{a}$), ($J_{b}$), ($J_{c}$) lần lượt là đường tròn đối xứng với đường tròn bàng tiếp góc A, B, C của tam giác ABC qua trung điểm BC, CA, AB. CMR P là tâm đẳng phương của 3 đường tròn nói trên. 

Gợi ý cũng là cách dựng của bài này: Gọi $D$ là điểm tiếp xúc của $(I)$ với $BC$. Kẻ đường kính $DD'$ của $(I)$;

                                                             $AD'$ cắt $(I)$ tại 1 điểm và điểm đó cũng chính là điểm tiếp xúc của đề bài 
Chứng minh đồng quy bằng cách dùng định lí Ceva.

 Cho tam giác ABC nội tiếp (O), có trực tâm H. Gọi N là trung điểm OH. Gọi D, E là hình chiếu của N lên AC, AB. CMR đường thẳng Ole của tam giác ADE đi qua trung điểm ON.

Bài này bạn dùng bổ đề Euler sau của thầy Linh: 
https://nguyenvanlin...2B0BEooupFFmxx0

Gọi trung điểm của đường trung bình ứng với A của tam giác ABC là P

Gọi đối xứng của N qua P là S thì S nằm trên AO 
Gọi trung điểm của AN là X thì XP song song với AO ( đường trung bình) 

Ta đi chứng minh $\angle PGA= \angle PHA$ (dễ dàng chứng minh bằng các tứ giác nội tiếp) 

Vậy P nằm trên đường thẳng Euler của ADE mà O cũng nằm trên đó

Vậy OP là đường thẳng Euler của ADE đi qua trung điểm ON 

 Tam giác nhọn ABC nội tiếp (O). Gọi F là điểm Toricelli của tam giác. FA, FB, FC cắt lại (O) tại X, Y, Z. CMR OF chia đôi đoạn nối trực tâm của hai tam giác ABC và XYZ. 

Gợi ý: $F$ cũng chính là điểm Fermat của tam giác $XYZ$

Tại đây, ta phát biểu một bổ đề: 

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ có $F$ là điểm Fermat. $FA, FB, FC$ cắt lại (O) tại $X, Y, Z$. Gọi $H$ là trực tâm của tam giác $XYZ$ thì $HF$ đi qua tâm đường tròn Euler của tam giác ABC. Áp dụng bổ đề này 2 lần, ta có điều phải chứng minh.

$\boxed{22}$: Cho $\Delta ABC$ nội tiếp $(O)$. Lấy $M$, $P$ thuộc $AB$ sao cho $AM$ $=$ $BP$. $N$, $Q$ thuộc $AC$ sao cho $AN$ $=$ $CQ$. $(AMN)$ và $(APQ)$ cắt $(O)$ tại $E$, $F$. $(AMN)$ cắt $(APQ)$ tại $D$. $G$ đối xứng với $A$ qua $D$. Chứng minh $AEGF$ là tứ giác điều hòa.
P/s: Đề kiểm tra lớp mk vừa rồi

Hehe :3 
Tóm tắt he  : Gọi $X,Y$ là trung điểm của $AB,AC$. Chứng minh được $A,X,D,Y$ đồng viên mà $A, X, O, Y$ đồng viên.

Suy ra: $G$ nằm trên $(O)$ 

Đến đây thì dễ rồi: Chứng minh $DA$ là phân giác $\angle FDE$. Từ đó ta được điều phải chứng minh thôi 

Cho $S$ là tập số thực thỏa: 
i/ $1 \in S$

ii/ $\forall a,b \in S, a-b \in S$ 

iii/ $a \in S, a \ne 0$ thì $\frac{1}{a} \in S$

Chứng minh rằng $\forall a,b \in S$ thì $ab \in S$.

- Giúp với ạ, em cảm ơn  

bài này vẫn có nghiệm nhé

Sorry, mình đã sửa lại > . <

Bài 12. Tìm tất cả các số nguyên dương $\displaystyle m$ và $\displaystyle p,q$ nguyên tố sao cho $\displaystyle 2^{m} p^{2} +1=q^{5}$

Bài 12.

Ta có: $2^mp^2+1=q^5 \Longleftrightarrow 2^mp^2=(q-1)(q^4+q^3+q^2+q+1)$

Xét $\text{gcd}(q-1,q^4+q^3+q^2+1)$

Ta có: $q^4+q^3+q^2+q+1=(q-1)(q^3+2q^2+3q+4)+5 \Longrightarrow \text{gcd}(q-1,q^4+q^3+q^2+q+1)\mid 5$

Xét trường hợp $q=2$: 

Suy ra: $\text{VP} \vdots 2 \Longrightarrow \text{VT} \vdots 2 \Longrightarrow 2^m=1 \Longrightarrow m=0$ (vô lí) 

Xét trường hợp $q > 2$ suy ra: $q-1$ chẵn và $q^4+q^3+q^2+q+1$ lẻ vì $\text{gcd}(q-1,q^4+q^3+q^2+q+1)\mid 5$

Nếu $\text{gcd}(q-1,q^4+q^3+q^2+q+1) = 5$ thì: $q-1=2^mp > q^4+q^3+q^2+q+1=p$ (vô lí) 

Suy ra: $\text{gcd}(q-1,q^4+q^3+q^2+q+1) = 1 \Longrightarrow q-1=2^m; q^4+q^3+q^2+q+1=p^2 (*)$ 

Xét $p=2 \Longrightarrow q=1$ (vô lí). Suy ra: $p>2$

$(*) \Longleftrightarrow q=2^m+1$. Xét $m$ lẻ: 

Suy ra: $\text{VP} \vdots 3 \Longrightarrow q=3 \Longrightarrow m=1, p=11$ (thỏa) 

Xét $m$ chẵn 
Nếu $m \geq 3$thì $q=2^m+1 \equiv 1 \pmod 8$
Suy ra: $p^2 \equiv 5 \pmod 8$ 
Không có $p$ thỏa mãn điều này. Vậy $m <3$

$m=2$ vô lí

Vậy ta có bộ nghiệm $(m,p,q)$ là $(1,11,3)$

Bài 10. Tìm tất cả các số nguyên dương $\displaystyle p,q,r,s >1$ thỏa mãn $\displaystyle p!+q!+r!=2^{s}$ (India Practice TST 2017)

Cho mình gửi link AoPS luôn nha   
Lời giải: https://artofproblem...1557175p9502820

Xét ảo zậy, nhưng vẫn thiếu 1 cặp nghiệm nữa nhé

À soggi, mình quên xét trường hợp 1 số bằng 2, từ đó mình đẩy lên là được $a,b$ lẻ xong mình xét ước nguyên tố   
Còn bộ nghiệm là $(a,b)=(1,2)$ và $(2,1)$.

Bài 8.Tìm các số nguyên dương $\displaystyle a,b$ thỏa mãn $\displaystyle a!+b!=a^{b} +b^{a}$

UwU bài 8:

Xét các ước nguyên tố thì ta sẽ chứng minh được $a=b$

Đến đây bài toán dễ rồi. Ta sẽ có nghiệm là $a=b=1$

Bài 4. Chứng minh rằng nếu $\displaystyle p$ là số nguyên tố thì $\displaystyle p^{3} +\frac{p-1}{2}$ không là tích hai số tự nhiên liên tiếp.

Bài 4 khá đơn giản:

Giả sử $p^3 +\frac{p-1}{2}=n(n+1)$ với $ n \in \mathbb{N} (*)$

$(*) \leftrightarrow 2p^3+p-1=2n(n+1).\text{VP} \vdots 4 \rightarrow 2p^3+p=p(2p^2+1) \equiv 1 \pmod 4$

Suy ra: $p \equiv  2p^2+1 \equiv 1$ hoặc $3 \pmod 4$ Trường hợp $p \equiv  2p^2+1 \equiv 1 \pmod 4$ vô lí

Vậy $p \equiv  2p^2+1 \equiv 3 \pmod 4 \rightarrow p=4k+3 (k \in \mathbb{N})$

Ta phát biểu 1 bổ đề: Nếu các số nguyên $x,y$ và $p \equiv 3 \pmod 4$ thỏa mãn $p \mid x^2+y^2$ thì:

$$p \mid x; p \mid y$$

$(*) \leftrightarrow p(2p^2+1)=(n+1)^2+n^2 \rightarrow (n+1)^2+n^2 \vdots p$

Áp dụng bổ đề thì ta được: $p \mid n, p \mid (n+1)$ mà ta có: $\text{gcd}(n+1,n)=1$ 

Điều này là điều vô lí. Vậy ta có đpcm

Bài 11. Tìm tất cả các số nguyên dương $\displaystyle n$ sao cho $\displaystyle 2^{n} -1|

Trường hợp $n=1$ là một trường hợp đúng.

Ta chứng minh $n>1$ là sai.

Dễ thấy nếu $n$ chẵn thì vô lí

Vậy $n$ lẻ. Suy ra: $2^n \equiv 8 \pmod {12} \rightarrow 2^n-1 \equiv 7 \pmod {12}$

Vì vậy $2^n-1$ có ít nhất một ước nguyên tố có dạng $12k \pm 5.$ Gọi số đó là $p$

Ta có: $\left(\frac{3}{p}\right) =1$. Theo luật tương hỗ Gauss thì: $\left(\frac{p}{3}\right)=(-1)^{\frac{p-1}{2}}.$

Mặt khác ta có: 

$$\left(\frac{p}{3}\right)=\left(\frac{\pm 2}{3}\right)= \pm 1$$

Suy ra: $(-1)^{\frac{p-1}{2}}= \pm 1$. Điều này vô lí nên ta có đpcm.

Bài 15.Tìm tất cả các số nguyên dương $\displaystyle m,n$ nguyên tố cùng nhau và $\displaystyle \varphi \left( 5^{m} -1\right) =5^{n} -1$

Bài 15.

Ta đi phản chứng giả sử $\text{gcd}(m,n)=1$. Ta đặt:

$$5^m-1=2^k.p^{a_1}_1.p^{a_2}_2...p^{a_t}_t$$

Trong đó $k \in \mathbb{N^*}, p_i \in \mathbb{P}, a_i \in \mathbb{N}, \forall i=\overline{1,t}$. Nếu $5^m -1$ không có ước nguyên tố lẻ thì $5^m-1 =2^k$. Khi đó ta có: $\varphi (5^m-1)=5^n-1=2^{k-1}$. Vì vậy:

$$5^m-1=2.5^n-2 \longleftrightarrow 2.5^n - 5^m=1$$

$\rightarrow$ Điều này là điều vô lí.

Vậy nên $5^m-1$ phải có ước nguyên tố lẻ. Ta có: 

$$\varphi (5^m -1) = 2^{k-1} \prod _{i=1}^{t}p_i^{a_1-1} \cdot \prod _{i=1}^{t}(p_i-1)=5^n-1$$

Theo phản chứng thì ta có:  $\text{gcd}(m,n)=1$

Suy ra: $\text{gcd}(5^m-1,5^n-1)=5^{\text{gcd}(m,n)}-1=5-1=4$

Do đó nếu $k \geq 3$ thì $5^m-1 \equiv 5^n-1 \equiv 0 \pmod 8$, mâu thuẫn. Nếu $k=1$ thì cũng vô lí.

Vậy $k=2$

Nếu tồn tại $j$ sao cho $a_j >1$ thì $5^m-1 \equiv 5^n-1 \pmod{p_j}$

Do $a_j=1, \forall i =\overline{1,t}$

Ta được: