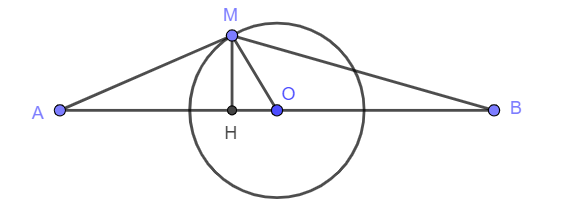
$\ast\quad MA+MB\ge AB,$ dấu bằng xảy ra khi $M$ nằm giữa $A$ và $B$ hay $M$ trùng với một trong hai giao điểm của $AB$ với $(O).$

$\ast\quad$Gọi $H$ là chân đường cao hạ từ $M$ xuống $AB.$ Đặt $\angle MOA=\alpha.$

      Ta có \begin{align*}MA+MB&=\sqrt{OA^2+OM^2-2OA\cdot OM\cdot\cos\alpha}+\sqrt{OB^2+OM^2+2OB\cdot OM\cdot\cos\alpha}\\ &\le \sqrt{2(OA^2+OB^2+2OM^2)} =2\sqrt{OA^2+OM^2} \end{align*}

Dấu bằng xảy ra khi $\cos\alpha=0$ hay $M$ nằm chính giữa một trong hai nửa cung tròn tâm $(O)$ chia bởi $AB.$

Vậy $P$ đạt GTNN khi $M$ trùng với một trong hai giao điểm của $AB$ với $(O),$ $P$ đạt GTLN khi $M$ nằm chính giữa một trong hai nửa cung tròn tâm $(O)$ chia bởi $AB.$

Câu hỏi phụ: có bao nhiêu cách đặt quân mã thỏa đề mà chúng không ăn nhau ?

 

Đã nhắc tới quân mã mà không đặt thêm một câu hỏi phụ như vậy thì phí quá

Vẫn sử dụng hình của bài trên 

Trong một bảng như vậy luôn có hai cột khác loại đứng cạnh nhau. Thấy rằng chỉ có cột $b$ và $e$ có thể đứng cạnh nhau để cho các quân mã không ăn nhau, do đó chỉ có $(bebe)$ và $(ebeb)$ thoả mãn đề bài.

Hình dưới là khả năng các cột có thể xảy ra.

Gọi $(xyzt)$ là một cách "lắp" các cột tạo thành bảng với $x,y,z,t$ lần lượt là cột thứ nhất, thứ hai, thứ ba, thứ tư tính từ trái sang phải.

Ta dễ nhận thấy các cách "lắp" thoả mãn là $(aaff),$ $(bbee),$ $(ccdd),$ $(abef),$ $(acdf),$ $(bcde)$ và các hoán vị của chúng.

Vậy có $3\cdot C^2_4+3\cdot 4!=90$ cách sắp xếp thoả mãn đề bài.

$2MA+3MB=2(MA+MB)+MB$ $\geq2AB=6\sqrt2,$ dấu bằng xảy ra khi và chỉ khi $\left\{\begin{matrix} M\in AB & \\ M\equiv B \end{matrix}\right.$ $\Leftrightarrow M\equiv B.$

Vậy tập hợp điểm $M$ thoả mãn $2MA+3MB\leq 6\sqrt{2}$ là điểm $B.$

$a^2+b^2+c^2+abc=4\Leftrightarrow a^2+bc.a+b^2+c^2-4=0.$ Coi $a$ là ẩn, ta có $\Delta=b^2c^2-4(b^2+c^2-4)$ $=(4-b^2)(4-c^2)\ge0.$

Do đó phương trình có hai nghiệm: $a_1=\frac{-bc+\sqrt{(4-b^2)(4-c^2)}}{2}$ và $a_2=\frac{-bc-\sqrt{(4-b^2)(4-c^2)}}{2}<0$ (loại). 

Ta có: \begin{align*}2a+b+c&=-bc+\sqrt{(4-b^2)(4-c^2)}+b+c\le-bc+\frac{8-b^2-c^2}{2}+b+c\\&=4-\frac{(b+c)^2}{2}+(b+c)=-\frac{1}{2}[(b+c)-1]^2+\frac{9}{2}\le\frac{9}{2} \end{align*}

Vậy ta có đpcm.

Câu này trong BTVN của mình nhưng có vẻ các bạn THCS cũng có thể làm được 

Tìm tất cả các cặp số thực $x,y$ thoả mãn $|xy|\le4$ và $(x-y)^2+20=(x+y)(xy-8).$

Câu 3: Đổi biến $(a,b,c)\mapsto(x^3,y^3,z^3),$ suy ra $xyz=1.$

Áp dụng bđt $m^3+n^3\geq mn(m+n)$ với $m,n$ dương, dấu bằng xảy ra tại $m=n$ ta có:

$C=\sum\frac{1}{a+b+1}=\sum\frac{1}{x^3+y^3+xyz}\leq\sum\frac{1}{xy(x+y)+xyz}=\sum\frac{1}{xy(x+y+z)}=1.$

Dấu bằng xảy ra khi và chỉ khi $x=y=z=1\Leftrightarrow a=b=c=1.$

Vậy $\min C=1\Leftrightarrow a=b=c=1.$

Ta có $x^2+4y^2\ge4xy\Leftrightarrow(x-2y)^2\ge0$ (đúng). Đẳng thức xảy ra khi $x=2y.$

$3x^2+2y^2=2x^2-2y^2+(x^2+4y^2)\ge2x^2-2y^2+4xy=10.$

Đẳng thức xảy ra khi $\left\{\begin{matrix} x=2y\\x^2-y^2+2xy=5 \end{matrix}\right.$ $\Leftrightarrow$ $\left\{\begin{matrix} x=\frac{2\sqrt{35}}{7}\\y=\frac{\sqrt{35}}{7} \end{matrix}\right.$ $\vee$ $\left\{\begin{matrix} x=-\frac{2\sqrt{35}}{7}\\y-=\frac{\sqrt{35}}{7} \end{matrix}\right.$

Vậy giá trị nhỏ nhất của biểu thức $3x^2+2y^2$ là $10,$ đạt tại $\left\{\begin{matrix} x=\frac{2\sqrt{35}}{7}\\y=\frac{\sqrt{35}}{7} \end{matrix}\right.$ hoặc $\left\{\begin{matrix} x=-\frac{2\sqrt{35}}{7}\\y-=\frac{\sqrt{35}}{7} \end{matrix}\right. .$

 

Nhận xét: Lời giải chính xác
Điểm: 10/10

Em xin lỗi, mong mod xoá đi bài trước của em do nhầm kí hiệu ạ, em cảm ơn ạ.
Dễ thấy $a(p)=a(2p),a(2p+1)=2p+1.$
Ta sẽ chứng minh $\sum_{n=k}^{2k-1} a(2n)=k^2 (k \in \mathbb{N}^{*}) (*).$
Thử với $n=1$ ta có $a(2)=1=n^2$ (thoả mãn).
Giả sử $n=i(i\in \mathbb{N}^{*})$ thoả mãn $(*)$, tức là $\sum_{n=i}^{2i-1} a(2n)=i^2.$
Cần chứng minh $n=i+1$ cũng đúng, hay $\sum_{n=i+1}^{2i+1} a(2n)=(i+1)^2.$
Thật vậy, ta có $\sum_{n=i+1}^{2i+1} a(2n)$ $=\sum_{n=i}^{2i-1} a(2n)-a(2i)+a(4i)+a(4i+2)$ $=i^2+a(2i+1)$ $=i^2+2i+1$ $=(i+1)^2, $ ta chứng minh được đẳng thức $(*).$
Vậy:
$\begin{align*} \sum_{n=2024}^{4048} a(n)&=\sum_{n=1012}^{2023} a(2n)+\sum_{n=1012}^{2023} a(2n+1)+a(4048) \\&=1012^2+\sum_{n=1012}^{2023} (2n+1)+253\\&=1024397+(2025+4047)\left(\frac{4047-2025}{2}+1\right)\div 2\\&=\boxed{4096829}.\end{align*}$
Trùng lặp

Dễ thấy $a(p)=a(2p),a(2p+1)=2p+1.$
Ta sẽ chứng minh $\sum_{n=k}^{2k-1} a(2n)=k^2 (k \in \mathbb{N}^{*}) (*).$
Thử với $n=1$ ta có $a(2)=1=n^2$ (thoả mãn).
Giả sử $n=i(i\in \mathbb{N}^{*})$ thoả mãn $(*)$, tức là $\sum_{n=i}^{2i-1} a(2i)=i^2.$
Cần chứng minh $n=i+1$ cũng đúng, hay $\sum_{n=i+1}^{2i+1} a(2i)=(i+1)^2.$
Thật vậy, ta có $\sum_{n=i+1}^{2i+1} a(2i)$ $=\sum_{n=i}^{2i-1} a(2i)-a(2i)+a(4i)+a(4i+2)$ $=i^2+a(2i+1)$ $=i^2+2i+1$ $=(i+1)^2, $ ta chứng minh được đẳng thức $(*).$
Vậy:
$\begin{align*} \sum_{n=2024}^{4048} a(n)&=\sum_{n=1012}^{2023} a(2n)+\sum_{n=1012}^{2023} a(2n+1)+a(4048) \\&=1012^2+\sum_{n=1012}^{2023} (2n+1)+253\\&=1024397+(2025+4047)\left(\frac{4047-2025}{2}+1\right)\div 2\\&=\boxed{4096829}.\end{align*}$

Nhận xét: Cách này tương tự như đáp án, tuy nhiên rõ ràng $\sum_{n=k}^{2k-1}a(2n)=\sum_{n=k}^{2k-1}a(n)$ nên không cần phải tách ra như vậy?

Một lời giải vô cùng thủ công, mong sẽ chính xác ạ.
Các số lẻ có ước số lẻ lớn nhất là chính nó.
Tổng các số lẻ từ 2024 đến 2048 là $(2025+4047)\left(\frac{4047-2025}{2}+1\right):2=3072432.\qquad(1)$
Xét các số tự nhiên chẵn từ 2024 đến 2048.
Số bé nhất và lớn nhất chia hết cho 2 mà không chia hết cho 4 là 2026 và 2046.
Số bé nhất và lớn nhất chia hết cho 4 mà không chia hết cho 8 là 2028 và 4044.
Số bé nhất và lớn nhất chia hết cho 8 mà không chia hết cho 16 là 2024 và 4040.
Số bé nhất và lớn nhất chia hết cho 16 mà không chia hết cho 32 là 2032 và 4048.
Số bé nhất và lớn nhất chia hết cho 32 mà không chia hết cho 64 là 2048 và 4000.
Số bé nhất và lớn nhất chia hết cho 64 mà không chia hết cho 128 là 2112 và 4032.
Số bé nhất và lớn nhất chia hết cho 128 mà không chia hết cho 256 là 2176 và 3968.
Số bé nhất và lớn nhất chia hết cho 256 mà không chia hết cho 512 là 2304 và 3840.
Số bé nhất và lớn nhất chia hết cho 512 mà không chia hết cho 1024 là 2560 và 3584.
Số chia hết cho 1024 mà không chia hết cho 2048 là 3072.
Số số chia hết cho 2048 là 2048.
Nhận xét: Nếu $a$ chia hết cho $2^k$ mà không chia hết cho $2^{k+1}$ thì $a+2^{k+1}$ cũng sẽ có tính chất như trên.
Do đó tổng ước số lẻ lớn nhất của các số:
Chia hết cho 2 mà không chia hết cho 4 là $\frac{2026+2030+...+2046}{2}=1013+1015+...+2023.$
Chia hết cho 4 mà không chia hết cho 8 là $\frac{2028+...+4044}{4}=507+...+1011.$
Chia hết cho 8 mà không chia hết cho 16 là $\frac{2024+...+4040}{8}=253+...+505.$
Chia hết cho 16 mà không chia hết cho 32 là $\frac{2032+...+4048}{16}=127+...+251+253.$
Chia hết cho 32 mà không chia hết cho 64 là $\frac{2048+...+4000}{32}=65+...+125.$
Chia hết cho 64 mà không chia hết cho 128 là $\frac{2112+...+4032}{64}=33+...+63.$
Chia hết cho 128 mà không chia hết cho 256 là $\frac{2176+...+3968}{128}=17+...+31.$
Chia hết cho 256 mà không chia hết cho 512 là $\frac{2304+...+3840}{256}=9+...+15.$
Chia hết cho 512 mà không chia hết cho 1024 là $\frac{2560+3584}{512}=5+7.$
Chia hết cho 1024 mà không chia hết cho 2048 là $\frac{3172}{1024}=3.$
Chia hết cho 2048 là $\frac{2048}{2048}=1.$
Tổng ước số lẻ lớn nhất của các số chẵn từ 2024 đến 4048 là $(1+3+5+...+2023)+253=1012^2+253=1024397.\qquad(2)$
Từ $(1)$ và $(2)$ suy ra $\sum_{n=2024}^{4048} a(n)=3072432+1024397=4096829.$
Nhận xét: Thêm một lời giải thủ công!
Điểm 9/10.

Nếu từ đầu không cho giả thiết là $\frac{1}{3}\le a,b,c\le3$ $(1)$ thì bài toán sẽ hay hơn. Ta sẽ đánh giá như sau:

$$11=a^2+b^2+c^2\le a^2+\frac{(b+c)^2}{2}=a^2+\frac{(5-a)^2}{2}\Rightarrow \frac{1}{3}\le a,b,c\le3.$$

Dễ dàng tính được $ab+bc+ca=7.$ Từ (1) ta suy ra được

$\left\{\begin{matrix} \left(a-\frac{1}{3}\right)\left(b-\frac{1}{3}\right)\left(c-\frac{1}{3}\right)\ge0 \\ (a-3)(b-3)(c-3)\le0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} abc\ge\frac{1}{27}+\frac{1}{3}(ab+bc+ca)-\frac{1}{9}(a+b+c)=\frac{49}{27}\\ abc\le27+3(ab+bc+ca)-9(a+b+c)=3 \end{matrix}\right.\Leftrightarrow\frac{49}{27}\le abc\le3.$

$abc$ đạt $\min$ tại $a=\frac{1}{3}, b=c=\frac{7}{3}$ và các hoán vị.

$abc$ đạt $\max$ tại $a=3, b=c=1$ và các hoán vị.

Vậy ...

Cho tập hợp $A=\left(-\infty;2m-3\right)$ và $B=\left(4-3m;8\right).$ Tìm $m$ sao cho $A\cap B$ có đúng 5 số nguyên.

P/s: Lâu lắm rồi mới quay lại diễn đàn.

Cho tam giác $ABC$ có $I$ là tâm đường tròn nội tiếp, đường tròn này tiếp xúc với cạnh $BC$ tại $D.$ Gọi $M$ là trung điểm của $BC.$ Chứng minh rằng $MI$ đi qua trung điểm của $AD.$

Chứng minh các đẳng thức lượng giác sau:

$a)\quad\tan9^{\circ}-\tan27^{\circ}-\tan63^{\circ}+\tan81^{\circ}=4.$ 

$b)\quad\tan20^{\circ}-\tan40^{\circ}+\tan80^{\circ}=3\sqrt3.$ 

$c)\quad \tan10^{\circ}-\tan50^{\circ}+\tan60^{\circ}+\tan70^{\circ}=2\sqrt3.$

$d)\quad \tan30^{\circ}+\tan40^{\circ}+\tan50^{\circ}+\tan60^{\circ}=\frac{8\sqrt3}{3}\cdot\cos20^{\circ}.$

Cho hai dãy số $(u_n)$ và $(v_n)$ được xác định như sau: $u_1=3,$ $v_1=2,$ $\left\{\begin{matrix} u_{n+1}=u_n^2+2v_n^2 \\ v_{n+1}=2u_nv_n \end{matrix}\right.$ với $n\ge1.$ Tìm công thức tổng quát của hai dãy $(u_n)$ và $(v_n).$

Bài 2:

Nếu ta chọn một số trong dãy $ a_1;a_2;...;a_{19},$ và một số trong dãy $b_1;b_2;...;b_{21}$ thì ta chọn được được có $19.21=399$ cặp. Từ điều kiện đề cho thì tổng của hai số đã chọn sẽ có giá trị từ $2$ đến $400,$ tổng có 399 giá trị. Nếu tồn tại đồng thời hai tổng có giá trị là $2$ và $400$ thì bốn số cần tìm là $(1;1;200;200).$ Nếu không thì khi này chỉ còn 398 giá trị cho 399 tổng, theo nguyên lý Dirichlet thì tồn tại hai tổng $a_i+b_k=a_j+b_l$ hay $a_j-a_i=b_l-b_k.$

Bài 1:

a) $10^{2023}+2024\equiv1^{2023}+2\equiv1+2\equiv0\pmod3$ nên $10^{2023}+2024$ chia hết cho $3.$

b) $n^3+2024n+2\equiv n^3-n+2=n(n-1)(n+1)+2\equiv2\pmod3$ (do $n(n-1)(n+1)$ là tích $3$ số nguyên liên tiếp nên chia hết cho 3), thu được $n^3+2024n+2$ không chia hết cho $3.$

Mà theo câu a) lại có $10^{2023}+2024$ chia hết cho 3 nên ta suy ra được $n^3+2024n+2$ không chia hết cho $10^{2023}+2024.$ 

Bài 3:

a) Ta có:

$3^{2n+1}-7\equiv 3^{2n}.3+3\equiv3(3^{2n}+1)\equiv3(9^n+1)\equiv3((-1)^n+1)\equiv 3(-1+1)\equiv0\pmod5$ (do $n$ là số nguyên lẻ).

$3^{2n+1}-7\equiv (-1)^{2n+1}-7\equiv -1-7\equiv 0\pmod4.$ 

Từ hai điều trên suy ra được $3^{2n+1}-7$ chia hết cho $20.$

b) Dễ thấy $n^4-2n^3+3n^2+2n-2$ là số chẵn nên $n^4-2n^3+3n^2+2n-2$ là số nguyên tố khi và chỉ khi nó bằng $2.$ 

Suy ra $n^4-2n^3+3n^2+2n-2=2$ $\Leftrightarrow n^4-2n^3+3n^2+2n-4=0 $ $\Leftrightarrow (n+1)(n−1)(n^2−2n+4)=0$ $\Leftrightarrow \left[\begin{matrix} n=1& \\  n=-1& \end{matrix}\right.$ (do $n$ là số tự nhiên).

Tiếp theo, ta định nghĩa một “tam giác” là một bộ $3$ vận động viên $a,b,c$ mà $a$ thắng $b$, $b$ thắng $c$ và $c$ thắng $a$. Ta có nhận xét sau: một giải đấu có cả $n$ vận động viên đều vô địch tương đối khi và chỉ khi mỗi cặp vận động viên đều nằm trong một tam giác nào đó.

Anh có thể nói kĩ về nhận xét được không ạ, nếu mỗi cặp vận động viên đều nằm trong một tam giác thì sẽ có cả $n$ vận động viên vô địch tương đối?

Ta sẽ chọn các số $x,y,z,t$ thoả mãn $xa^4b+yb^4c+zc^4d+td^4a\geq a^2bcd.$

Sử dụng $\text{Weighted AM-GM}$ ta được

\begin{align*} xa^4b+yb^4c+zc^4d+td^4a&\geq(x+y+z+t)\cdot\sqrt[x+y+z+t]{(a^4b)^x\cdot(b^4c)^y\cdot(c^4d)^z\cdot(d^4a)^t}\\&=(x+y+z+t)\cdot\sqrt[x+y+z+t]{a^{4x+t}b^{4y+x}c^{4z+y}d^{4t+z}} \end{align*}

Chọn $x+y+z+t=1,$ đồng nhất các tham số ta được $\left\{ \begin{array}{l} 4x + t = 2\\ 4y + x = 1\\ 4z + y = 1\\4t + z = 1 \end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \frac{23}{51}\\y = \frac{7}{51}\\z = \frac{11}{51}\\t = \frac{10}{51}\end{array} \right.  .$

$\ast$

$\ast$     $\ast$

Sử dụng bất đẳng thức $\text{AM-GM}$ ta có

\begin{align*}a^4b +b^4c + c^4d +d^4a &=\sum\left(\frac{23}{51}a^4b +\frac{7}{51}b^4c + \frac{11}{51}c^4d + \frac{10}{51}d^4a\right)\\&=\frac{1}{51}\sum(23a^4b +7b^4c + 11c^4d +10d^4a)\\&\geq\frac{1}{51}\left(\sum51\sqrt[51]{a^{23\cdot4+10}b^{23+7\cdot4}c^{7+11\cdot4}d^{11+10\cdot4}}\right)\\&=\sum a^2bcd=abcd(a+b+c+d)\end{align*}

Vậy ta có đpcm.

Trong một giải đấu bóng bàn nam có $n$ $(n\geq3)$ vận động viên tham gia, hai vận động viên bất kì thi đấu với nhau đúng một trận (không có kết quả hoà). Kết thúc giải đấu, mỗi vận động viên sẽ viết ra tên những đối thủ thua mình và tên những vận động viên thua một trong các đối thủ đó. Một vận động viên được gọi là vô địch tương đối nếu anh ta viết được tên của tất cả $n-1$ đối thủ còn lại. Gọi $S_n$ là số vận động viên vô địch tương đối nhiều nhất có thể.

a) Tính $S_3,S_4.$

b) Chứng minh rằng $S_n=n$ với mọi $n\geq5.$

 

P/s: các mod cho em hỏi ở phần tiêu đề các bài tổ hợp cần tóm tắt không ạ?

$1,$ 

Xét $x=3$ thoả mãn phương trình.

Xét $x>3$ thì $\sqrt[5]{x-2}+\sqrt[7]{x-3}>1$ còn $\sqrt[3]{4-x}<1,$ không thoả mãn.

Xét $x<3$ thì $\sqrt[5]{x-2}+\sqrt[7]{x-3}<1$ còn $\sqrt[3]{4-x}>1,$ không thoả mãn.

Vậy phương trình có tập nghiệm $S=\{3\}.$

Cho $n,a,b$ là các số nguyên dương. Chứng minh $(n^a-1,n^b-1)=n^{(a,b)}-1.$  

Chỗ này mình chưa hiểu. 

$\angle KEC=\angle AEF=\frac{180^{\circ}-\angle A}{2}$ (do $\bigtriangleup AEF$ cân tại $A$).

$\angle KIC=180^{\circ}-\angle BIC=180^{\circ}-\left(180^{\circ}-\angle BIC-\angle BCI\right)=\frac{\angle ABC}{2}+\frac{\angle ACB}{2}=\frac{180^{\circ}-\angle A}{2}.$

Suy ra $\angle KEC=\angle KIC.$

Xét tứ giác $IEKC$ có $\angle KEC=\angle KIC$ nên là tứ giác nội tiếp.

Do đó $\angle IKC=\angle IEC=90^{\circ},$ thu được $BK\perp KC.$

Vậy ta có đpcm.