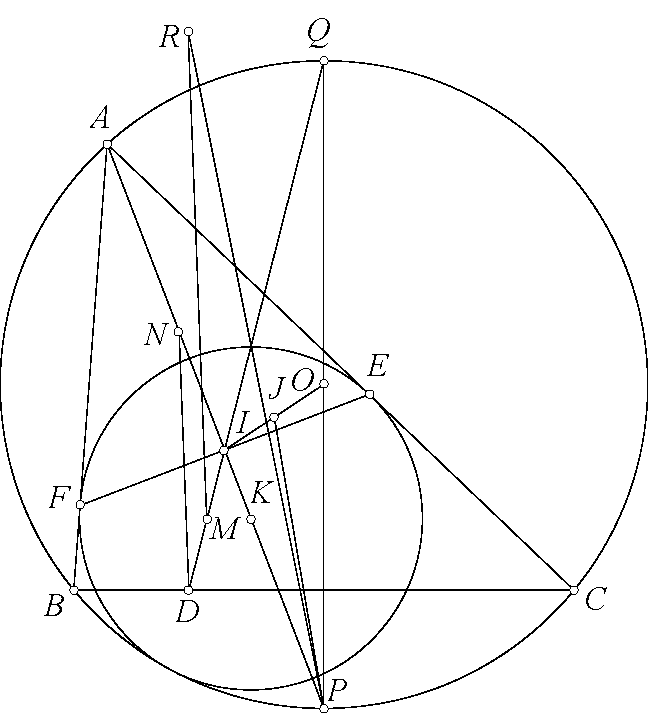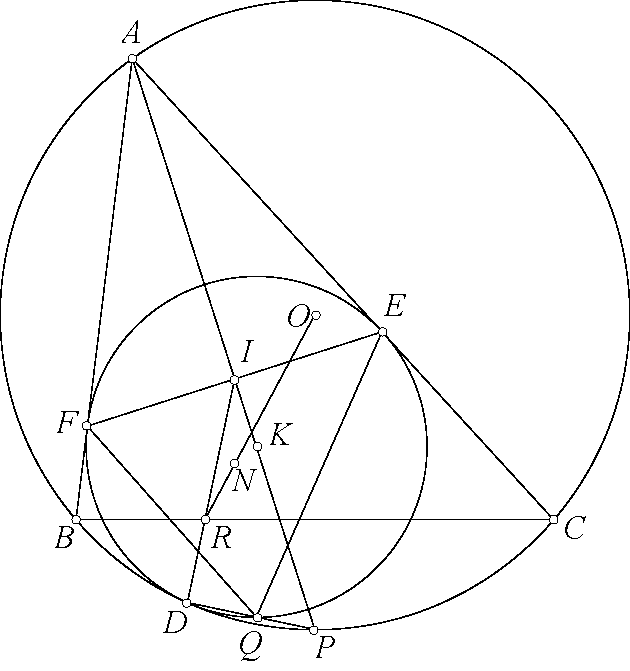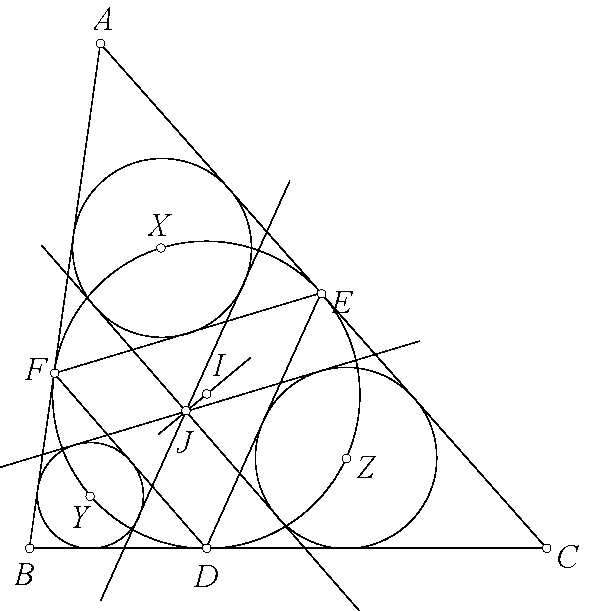$(AID)$ trực giao với $(O)$ qua nghịch đảo tương đương với $I_aD$ vuông góc $BC$ với $(I_a)$ tiếp xúc $BC$ tại $D$ mà em, cái này có thể coi là hiển nhiên mà.

Cám ơn em đã đóng góp xây dựng, mọi đóng góp ở mức độ nào đều là đáng trân trọng. Ai cũng phải học hỏi vì kiến thức là vô hạn kể cả trong nội tại hình học sơ cấp, thầy cũng phải luôn học tập và cố gắng hơn.

Nói qua về bài tập này http://artofproblems...c6t48f6h1368124, mình có 1 phát hiện nhỏ, nếu định nghĩa các điểm $Y,Z$ tương tự thì $IX=IY=IZ$ nói cách khác ta có thể chứng minh được $AX,BY,CZ$ đồng quy.

Ta đưa bài toán 120 về bài toán sau

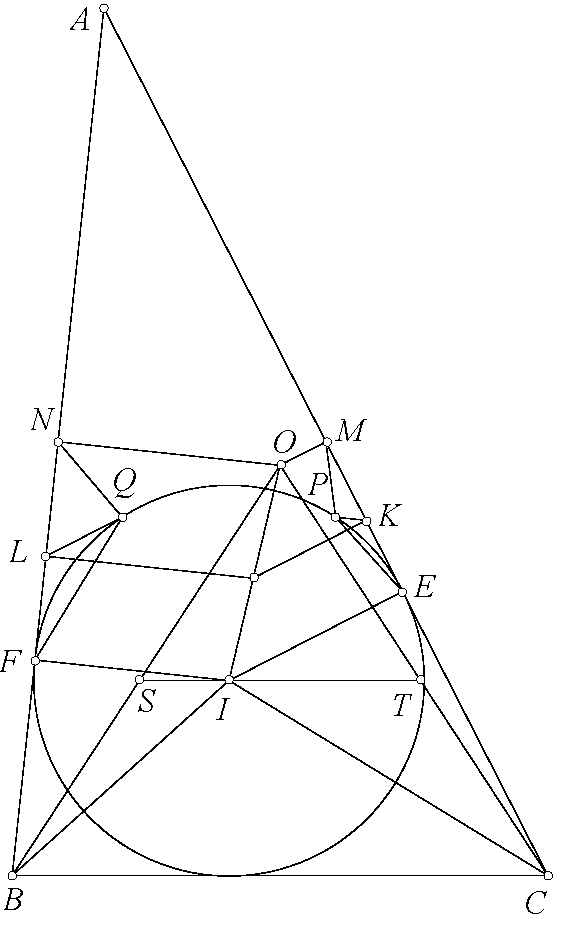
Bài toán 120'. Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $CA,AB$ tại $E,F$. $P,Q$ lần lượt đối xứng với $E,F$ qua $IB,IC$. $K,L$ thuộc $CA,AB$ sao cho $PK\perp AB,QL\perp AC$. Chứng minh rằng đường thẳng qua $K,L$ lần lượt vuông góc $CA,AB$ cắt nhau trên đường thẳng $OI$ của $ABC$.

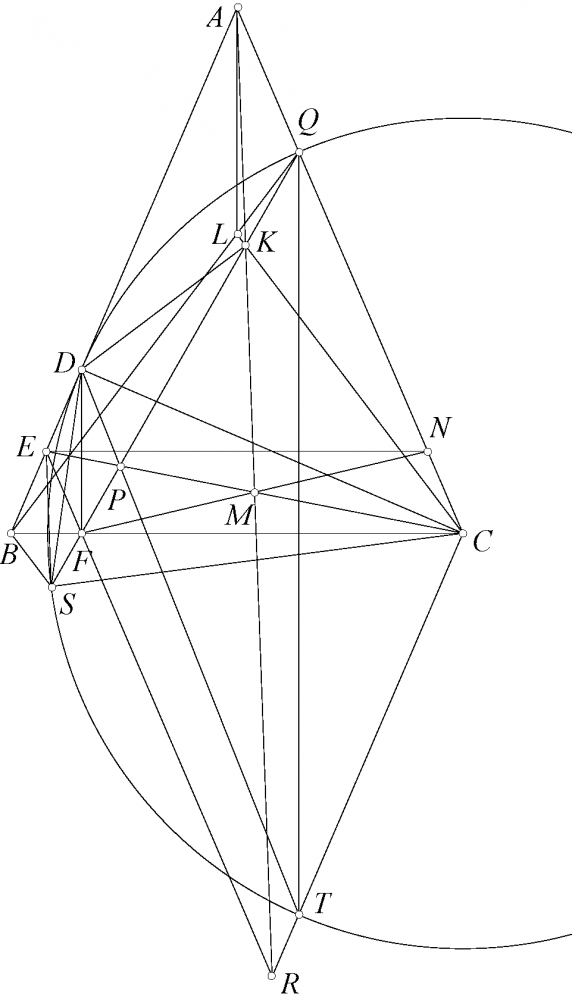
Lời giải. Gọi $O$ là tâm ngoại tiếp tam giác $ABC$ và $M,N$ là hình chiếu của $O$ lên $CA,AB$. Đường thẳng qua $I$ song song $BC$ cắt $OB,OC$ tại $S,T$. Dễ thấy hai tam giác $FQN$ và $CIO$ đồng dạng c.g.c mặt khác hai tam giác $FQL$ và $CIT$ đồng dạng g.g nên $\frac{LF}{LN}=\frac{TC}{TO}$. Tương tự $\frac{KE}{KM}=\frac{SB}{SO}$ do đó theo định lý Thales thì $\frac{LF}{LN}=\frac{KE}{KM}$ theo bổ đề quen thuộc dễ thấy các đường thẳng qua $K,L$ lần lượt vuông góc $CA,AB$ cắt nhau trên đường thẳng $OI$ của $ABC$.

Bài toán 121. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, tâm nội tiếp $I$. Đường tròn $(K)$ tiếp xúc $CA,AB$ tại $E,F$. $AI$ cắt $(O)$ tại $P$ khác $A$. $PQ$ là đường kính của $(O)$. $QI$ cắt $BC$ tại $D$. $M,N$ là trung điểm của $DI$ và $KA$. Đường thẳng qua $M$ song song $DN$ cắt trung trực $AQ$ tại $R$. Gọi $J$ là trung điểm $OI$. Chứng minh rằng $\angle APR=\angle QPJ$.

Cám ơn Bảo, rất vui khi thấy sự trở lại của em. Theo đề nghị của em, thầy đề nghị một bài mới như sau

Bài toán 116. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ với tâm nội tiếp $I$. Đường tròn $(K)$ tiếp xúc $CA,AB$ tại $E,F$ và tiếp xúc trong $(O)$ tại $D$. $AI$ cắt $(O)$ tại $P$ khác $A$. $PD$ cắt $(K)$ tại $Q$ khác $D$. $DI$ cắt $BC$ tại $R$. Chứng minh rằng $RO$ đi qua tâm đương tròn Euler tam giác $QEF$.

@Trong topic này những bài nào mình post mà tự sáng tác mình sẽ không ghi gì cả, còn những bài không phải của mình mình sẽ ghi rõ.

Lời giải bài toán 104. 

Bổ đề. Cho tam giác $ABC$, $I_a$ là tâm đường tròn bàng tiếp ứng với $\angle A$. $M$ đối xứng $I_a$ qua $BC$. Khi đó $AM$ song song với đường thẳng $Euler$ của tam giác $I_aBC$.

Chứng minh sau của bạn Đỗ Xuân Long lớp 11 toán THPT chuyên KHTN.

Chứng minh. Gọi $X$ là điểm chính giữa cung $BC$ không chứa $A$, $H$ là trực tâm tam giác $I_aBC$. Ta có $\triangle I_aXB\sim \triangle I_aCM$ nên $I_aM\cdot I_aX=I_aB\cdot I_aC$. Mặt khác do $\frac{1}{2}\angle A+\angle BI_aC=90^\circ$ nên $\triangle I_aHC\sim\triangle I_aBA$ suy ra $I_aH\cdot I_aA=I_aB\cdot I_aC$. Từ đó $I_aX\cdot I_aM=I_aH\cdot I_aA$ nên theo định lý Thales, $AM\parallel XH$.

Giải bài toán. $I$ là tâm đường tròn nội tiếp tam giác $ABC$. Chú ý rằng đường tròn tâm $A_1$ qua $A$, $C$ trực giao với đường tròn $(AIB)$ và đường tròn tâm $A_2$ qua $A$, $B$ trực giao với $(AIC)$. Xét hợp của phép nghịch đảo cực $A$ phương tích $AB\cdot AC$ với phép đối xứng qua phân giác $\angle A$. Dưới phép biến hình này, $U$ biến thành trực tâm tam giác $JBC$. $D$ biến thành giao điểm của $AD$ với đường tròn $(ABC)$. Từ đó đường tròn $(ADU)$ biến thành đường thẳng Euler của tam giác $JBC$. Theo bổ đề trên thì nếu gọi $K$ là đối xứng của $J$ qua $BC$ thì $AK$ song song với đường thẳng Euler của tam giác $JBC$. Do đó theo nghịch đảo thì tiếp tuyến tại $A$ của $(ADU)$ đi qua ảnh nghịch đảo của $I$ qua đường tròn $(ABC)$. Tương tự ta suy ra các tiếp tuyến qua $A$, $B$, $C$ của các đường tròn $(ADU)$, $(BEV)$, $(CFW)$ đồng quy.

Chú ý. Phép nghịch đảo bảo toàn sự đối xứng. Người ta còn gọi phép nghịch đảo qua một đường tròn là phép đối xứng qua đường tròn. Sự bảo toàn tính đối xứng có thể phát biểu như sau: trong mặt phẳng, cho trước hai điểm $A$ và $B$ đối xứng nhau qua một đường tròn $\mathcal{C}$(có thể suy biến thành đường thẳng), ảnh của $A$ và $B$ dưới một phép nghịch đảo sẽ đối xứng qua ảnh của $\mathcal{C}$ cũng dưới phép nghịch đảo đó.

Xin cám ơn bạn Ngô Quang Dương sinh viên ĐHKHTN đã giúp tôi biên tập lời giải này.

Bài toán 105.(Mở rộng ý a) VMO 2017 bài toán 3). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Một đường tròn $(K)$ đi qua $B,C$ cắt $CA,AB$ tại $E,F$ khác $B,C$. $BE$ cắt $CF$ tại $H$. $AH$ cắt $(O)$ tại $D$ khác $A$. Tiếp tuyến tại $E,F$ của $(K)$ lần lượt cắt $DB,DC$ tại $M,N$. Chứng minh rằng $MN\perp OH$.

Cảm ơn Quân và Khánh, bài toán 133 thầy chế lại từ đây http://artofproblems...nity/c6h1279917, mục đích của thầy là lấy điểm $R$ thuộc $MN$ sao cho $AR\perp EF$ rồi sau đó chứng minh $BQ,CP$ đi qua $R$ nhưng Quân chứng minh cách khác đẹp. Chú ý rằng bài toán này và bài toán của Khánh có thể đúng với $H$ bất kỳ thay vì trực tâm. Nhưng để chứng minh $AR\perp EF$ thì cần $H$ là trực tâm.

Bài toán 134. Cho tam giác $ABC$ và $DEF$ là tam giác pedal của $P$ bất kỳ. $(DEF)$ cắt $BC$ tại $G$ khác $D$. Đường thẳng qua $P$ vuông góc với $EF$ cắt $DE,DF$ tại $M,N$. Đường tròn $(DMN)$ cắt $(DEF)$ tại $Q$ khác $D$. Lấy $T$ sao cho $TM\perp AC,TN\perp AB$. $AT$ cắt $BC$ tại $S$. Chứng minh bốn điểm $A,Q,G,S$ đồng viên.

Bài toán 133' của Khánh có thể viết dưới dạng tứ giác như sau

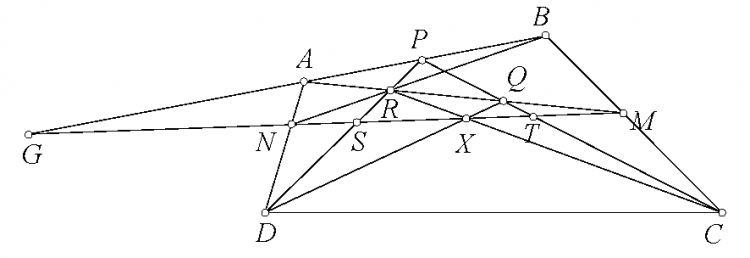
Bài toán 133'. Cho tứ giác $ABCD$ với $P,M,N$ lần lượt thuộc $AB,BC,AD$. $PC,PD$ lần lượt cắt $AM,BN$ tại $Q,R$. Chứng minh rằng $DQ,CR,MN$ đồng quy.

Giải. Gọi $MN$ cắt $ABPD,PC$ lần lượt tại $G,S,T$. Ta thấy $(PS,DR)=N(PS,DR)=(PG,AB)=M(PG,AB)=M(PT,QC)=(PT,QC)$ suy ra $DQ,CR,MN$ đồng quy.

Lời giải bài toán 160.

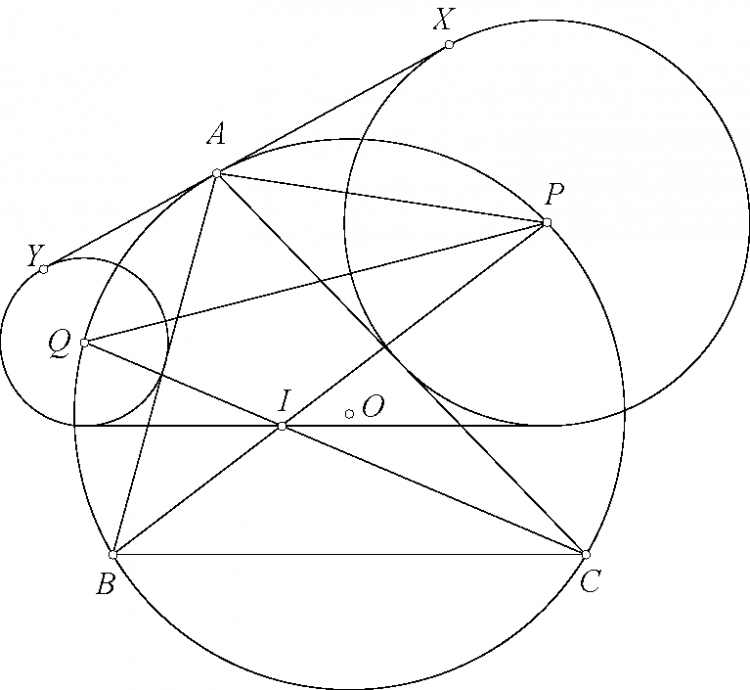
Bổ đề. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ tâm nội tiếp $I$. $IB,IC$ cắt $(O)$ tại $P,Q$. Gọi $(P)$ là đường tròn tâm $P$ tiếp xúc $AC$. Gọi $(Q)$ là đường tròn tâm $Q$ tiếp xúc $AB$. Chứng minh rằng có một tiếp tuyến chung của $(P),(Q)$ đi qua $I$.

Chứng minh. Vẽ $AX$ tiếp xúc $(P)$ thì $\angle XAC=2\angle PAC=2\angle PBC=\angle ABC$. Từ đó $AX$ là tiếp tuyến của $(O)$. Tương tự $AY$ tiếp xúc $(Q)$ thì $AY$ là tiếp tuyến của $(O)$ nên $X,Y,A$ thẳng hàng. Vậy tiếp tuyến chung ngoài của $(P),(Q)$ đi qua $A$. Qua đối xứng trục $PQ$ thì tiếp tuyến chung ngoài còn lại đi qua $I$.

Giải bài toán. Dễ thấy tâm $X$ của đường tròn nội tiếp tam giác $AEF$ là trung điểm cung $EF$ của $(I)$. Tương tự với các đường tròn $(Y),(Z)$. Do đó theo bổ đề thì tiếp tuyến chung ngoài khác $BC$ của $(Y),(Z)$ đi qua tâm $J$ nội tiếp tam giác $DEF$. Tương tự với các tiếp tuyến chung của $(Z),(X)$ và $(X),(Y)$. Dễ thấy do $J$ là tâm nội tiếp $DEF$ và $I$ là tâm ngoại tiếp $DEF$ nên đường thẳng $IJ$ là đường thẳng Euler của tam giác pedal của $J$ với $DEF$ nên $IJ$ đi qua $G$ là trọng tâm của tam giác pedal của $J$.

Bổ đề này thực chất là bài toán vô địch Nga năm nào đó, kết quả bài toán 160 cũng đã có trên AoPS.

Bài toán 163 (AoPS). Cho tam giác $ABC$ với tâm nội tiếp $I$ và $P$ thỏa mãn $\angle PIA=90^{\circ}$. $Q$ là đẳng giác của $P$ với $ABC$. $D$ thuộc $BC$ sao cho $PD\parallel AQ$. Chứng minh rằng đường tròn đường kính $\odot(AP)$ tiếp xúc đường tròn đường kính $\odot(QD)$. 

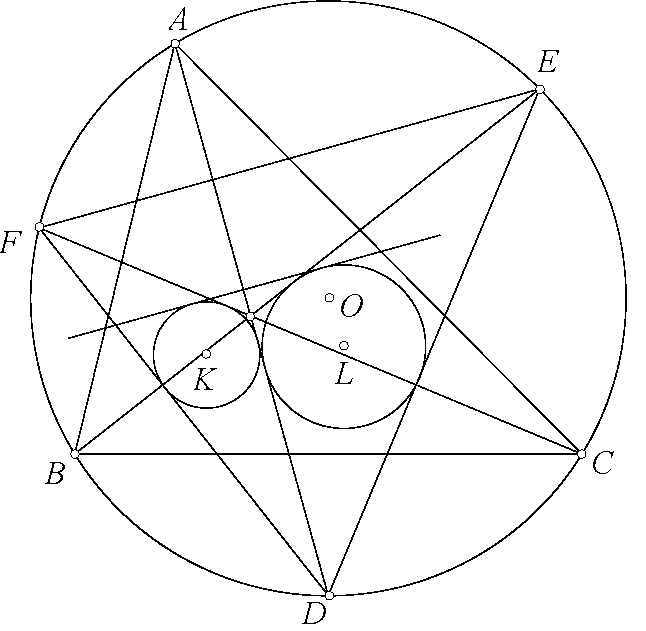
Lời giải bài toán 161. Xét đường tròn $\Gamma$ đi qua $I$ và tiếp xúc với $\omega_1,\omega_2$. Ta cần chứng minh $\Gamma$ tiếp xúc $IBC$. Gọi $IA,IB,IC$ cắt $(O)$ ngoại tiếp tam giác $ABC$ tại $D,E,F$. Xét phép nghịch đảo cực $I$ phương tích $k=\overline{IA}.\overline{ID}=\overline{IB}.\overline{IE}=\overline{IC}.\overline{IF}$ khi đó các đường tròn $\omega_1,\omega_2$ biến thành đường tròn $(K),(L)$ nội tiếp tam giác $IDF,IDE$. Ta cần chứng minh có tiếp tuyến chung của $(K),(L)$ song song $EF$.

Bài toán này đã có tại đây.

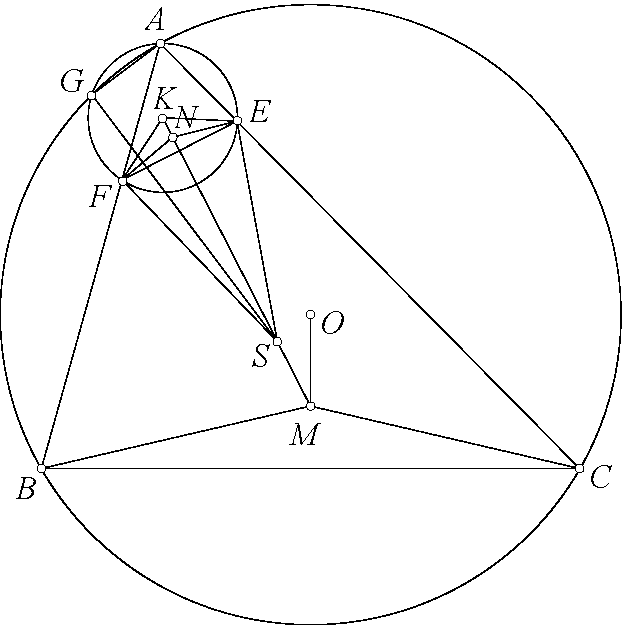
Bài toán 162. Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. $M$ bất kỳ trên trung trực $BC$ và nằm trong tam giác $ABC$. $E,F$ thuộc $CA,AB$ sao cho $ME=MF$. $N$ nằm trong tam giác $AEF$ sao cho $\triangle NEF\sim\triangle MBC$. $(K)$ là đường tròn ngoại tiếp tam giác $AEF$. $S$ là nghịch đảo của $N$ qua $(K)$. $(K)$ cắt $(O)$ tại $G$ khác $A$. Chứng minh rằng $\angle AGS=90^\circ$.

Cám ơn Hoàng về lời giải mới thú vị khác đáp án, thầy sẽ post đán án ngày mai. Xin đề nghị bài tiếp theo

Bài toán 148 (Telv Cohl). Cho tam giác $ABC$ có $P,Q$ là hai điểm đẳng giác và $E,F$ lần lượt thuộc cạnh $CA,AB$. Chứng minh rằng $ \angle BPC + \angle EPF = 180^{\circ} \iff \angle BQC + \angle EQF = 180^{\circ}$

Cám ơn Bảo với lời giải rất nhanh, thầy đề nghị bài mới cho topic tiếp tục

Bài toán 139 (Nguyễn Lê Phước).  Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. $DE,DF$ cắt $AB,AC$ tại $M,N$. $IE,IF$ cắt $AB,AC$ tại $P,Q$. Chứng minh rằng trung điểm của $MN,PQ,BC$ thẳng hàng.

Mình có post một tổng quát cho tính chất của bài toán 99. tại đây http://artofproblems...h498545p2801321 đã lâu, đó là một mở rộng sang conic, lời giải của Luis hay nhưng cũng phức tạp. Mở rộng này không gần gũi với toán Olympic lắm vậy hãy chỉ để tham khảo.

Như vậy VMF's Marathon Hình học Olympic đã đạt tới 100 bài. Trong giai đoạn cuối thi VMO và vòng 2 thì topic này khá thiết thực. Do đó mình xin thay đổi một chút nội quy cho VMF's Marathon Hình học Olympic sôi động hơn.

- Đánh số bài bôi đen theo thứ tự liên tục.

- Người giải xong thì nên đề nghị một bài toán nếu lấy ở đề thi hoặc AoPS hoặc các nguồn trên mạng thì kèm trích dẫn. Có thể nhờ người đề nghị.

- Một bài để không quá 2 ngày, nếu đủ 2 ngày mà không ai giải thì người đề nghị có thể post đáp án. Nếu quá 2 ngày người đề nghị không post đáp án thì tôi hoặc BQT sẽ xóa bài đó và thay vào đó đề nghị khác có đáp án cẩn thận vào chính số thứ tự đó.

- Nên viết lời giải kèm hình vẽ và không dẫn link giải. Người giải viết lại lời giải tiếng Việt nếu tham khảo ở link nào đó và dẫn lại link tham khảo cuối bài giải.

Hy vọng thời gian tới mình đủ sức tuyển tập và biên tập các bài toán ở topic này thành một Ebook hình học của VMF. Chúc các bạn mọi việc may mắn và topic sẽ lại được các bạn tham gia nhiệt tình.

Trân trọng.

Trần Quang Hùng.

Ủng hộ ý kiến của viet nam in my heart, chúng ta nên dành thêm chút thời gian để đọc và phản biện lời giải đưa lên.

Lời giải của Khoa đúng rồi. Được Dương đồng ý, mình đề nghị một bài mới, bài này mình phát triển từ một bài toán Khoa post trên facebook

$\boxed{\text{Bài toán 53.}}$ Cho tam giác $ABC$ và $P$ nằm trên đường tròn đường kính $BC$. $PB,PC$ cắt $CA,AB$ tại $E,F$. Chứng minh rằng tâm đường tròn pedal của $P$ ứng với $ABC$ nằm trên đường nối trung điểm $BE,CF$.

Theo mình không nên phân biệt đối xử với tọa độ, đặc biệt là tọa độ Barycentric vì không phải vô cớ mà tờ báo hình sơ cấp lớn nhất thế giới  http://forumgeom.fau.edu/, đã nhiều năm qua dành thời lượng lớn để nghiên cứu về loại tọa độ này. Hơn nữa thực chất những việc biến đổi tỷ số trên đường thẳng, rồi những hệ thức của hàng điểm điểu hòa đều có gốc gác là đại số và tọa độ xạ ảnh. Mặt khác cũng không phải không có lý do mà Descartes được xếp vào một trong những nhà toán học vĩ đại nhất nhờ phương pháp của mình. Do đó nên dung hòa giữa đại số và hình.

Cấu hình của bài thầy Hà trong bài đề nghị của Khánh là cấu hình rất thú vị, trên đó khai thác được khá nhiều điểm đặc biệt các tam giác $AA_bA_c,BB_cB_a,CC_aC_b$ mà những tâm đặc biệt của tam giác tạo bởi các tâm trên nằm trên đường thẳng $OI$ của $ABC$.

Mình ví dụ một bài như sau

Giữ nguyên đề của Khánh. Gọi $O_a,O_b,O_c$ là tâm ngoại tiếp tam giác $AA_bA_c,BB_cB_a,CC_aC_b$. Chứng minh rằng trọng tâm tam giác $O_aO_bO_c$ nằm trên đường thẳng $OI$ của $ABC$.

Các giải khác cho bài 5 (dùng hình của Bảo) tránh dùng sin, chú ý hai tam giác $XBF$ và $XEC$ đồng dạng nên tỷ lệ diện tích là bình phương tỷ lệ đồng dạng.

Gọi $AX$ cắt $BC$ tại $U$ thì $\frac{UB}{UC}=\frac{[XAB]}{[XAC]}=\frac{[XAB]}{[XBF]}.\frac{[XBF]}{[XEC]}.\frac{[XEC]}{[XAC]}=\frac{AB}{BF}.\frac{BF^2}{CE^2}.\frac{CE}{AC}=\frac{AB.BF}{AC.CE}$. Tương tự dùng Ceva ta có điều phải chứng minh.

Chú ý hai tam giác $XBF$ và $XEC$ đồng dạng cùng hướng, ta có thể thay bằng diện tích đại số và độ dài đại số.

Lâu mình không tham giải, thực sự là phát hiện của Dương ở bài 54 khá thú vị. Nhân một bài Bảo vừa hỏi, mình thấy bài này có ý tưởng khá giống nên giải thử theo cách phương tích.

Sửa lại ký hiệu như sau cho tiện.

Cho tam giác $ABC$ trực tâm $H$. Dựng vào trong tam giác $PBC$ vuông cân tại $P$. Gọi $Q$ đẳng giác $P$ trong tam giác $ABC$. Chứng minh rằng $PQ$ đi qua $H$.

Lời giải. Do $Q$ đẳng giác $P$ nên gọi $E,F$ là hình chiếu của $Q$ lên $CA,AB$ dễ thấy tam giác $QFB$ và $QEC$ vuông cân. Vậy trong tam giác $QBC$ các tam giác $QFB$ và $QEC$ vuông cân dựng ra ngoài và tam giác $PBC$ vuông cân dựng vào trong nên $EPQF$ là hình bình hành từ đó dễ thấy $P$ là trực tâm tam giác $AEF$. Như vậy dễ thấy $P,H$ đều nằm trên trục đp của đường tròn đường kính $BE,CF$. Gọi $K,L$ là hình chiếu của $C,B$ lên $QF,QE$. Dễ thấy hai tam giác vuông $QCK$ và $QBL$ đồng dạng nên $QK/QL=QC/QB=QE/QF$ hay $QF.QK=QE.QL$. Từ đó $Q$ cũng thuộc trục đp của đường tròn đường kính $BE,CF$.

Bài toán này có phát biểu khá gần kiểu hình lớp 7, không rõ có cách nào THCS không ?

$\boxed{\text{Bài toán 55.}}$. Cho tam giác $ABC$ nhọn nội tiếp trong đường tròn $(O)$. Tiếp tuyến tại $A$ của $(O)$ cắt $BC$ tại $T$. $P$ nằm trong tam giác sao cho $TP=TA$. $PA,PB,PC$ lần lượt cắt $(O)$ tại $D,E,F$ khác $A,B,C$. Dựng tam giác cân $BAQ$ đồng dạng cùng hướng với $FOD$ và tam giác cân $CAR$ đồng dạng cùng hướng với $EOD$. Chứng minh rằng tâm ngoại tiếp tam giác $PQR$ nằm trên $AO$.

Bài toán 61 lời giải trên báo dùng phương tích cũng rất hay, lời giải này và của Quân (halloffame) đều khác với đáp án mình làm. Ai có thể đưa lời giải của báo lên không ?

Có một lưu ý nhỏ là bài toán 60 có nguồn gốc từ tạp chí Mathematical Reflections, sau đó nó được Telv Cohl tổng quát trên AoPS như sau

$\boxed{\text{Bài toán 60'.}}$ Cho tam giác $ABC$ nội tiếp $(O)$. Các đường tròn mixtilinear nội ứng với $A,B,C$ là $(O_a),(O_b),(O_c)$ lần lượt tiếp xúc $(O)$ tại $D,E,F$. $P$ nằm trên đường thẳng $OI$. $PD,PE,PF$ lần lượt cắt $(O_a),(O_b),(O_c)$ tại điểm thứ hai $X,Y,Z$. Chứng minh rằng $AX,BY,CZ$ đồng quy.

Trường hợp bài toán 60 là khi $P$ trùng $O$. Tuy nhiên bài toán tổng quát này khá khó, mình đưa lên là để cùng thảo luận, biết đâu có một lời giải hay cho bài này. Mặc dù vậy bài toán 60 gốc cũng đủ hay.

Bổ đề. Cho tam giác $ABC$ cân tại $A$ có đường cao $CD$. Gọi $E$ là trung điểm của $BD$, $M$ là trung điểm $CE$, phân giác của $\angle{BDC}$ cắt $CE$ tại $P$. Đường tròn tâm $C$ bán kính $CD$ cắt $AC$ tại $Q$. Gọi $K$ là giao điểm của $PQ$ và $AM$.

$\boxed{\text{Bài toán 78.}}$ Cho tam giác $ABC$ có các tâm bàng tiếp góc $B,C$ là $K,L$. Lấy $P,Q$ trên $CK,BL$ sao cho $LP\parallel AC,KQ\parallel AB$. $PQ$ cắt $KL$ tại $R$. $H$ là hình chiếu của $R$ lên đường thẳng $OI$ của tam giác $ABC$. $AD$ là phân giác của tam giác $ABC$. $K$ thuộc $AD$ sao cho $KH\perp HA$. $HB,HC$ cắt $(HKD)$ tại $M,N$ khác $H$. $DN,DM$ cắt $CA,AB$ tại $E,F$. Chứng minh rằng bốn điểm $A,E,H,F$ thuộc một đường tròn.

Bài tập tập huấn đội IMO 2016.

Bài toán mà viet nam in my heart, nói có 3 hướng tiếp cận khác nhau

- Phương pháp vector : Biểu diễn vector $\vec{XL}$ theo $\vec{XY},\vec{XZ}$ và $k$ với $\vec{OL}=k\vec{OA}$ rồi chiếu xuống $XY$.

- Hàng điều hòa: Có thể bắt chước tương tự cách chứng minh đẳng giác của điểm Nagel nằm trên đường thẳng $OI$ (của tam giác $XYZ$), giờ ta sẽ chỉ ra $XL$ là đẳng giác trong góc $X$ của $XJ$ với $J$ là một điểm xác định trên đường thẳng $OI$.

- Giải bài tổng quát hơn: chính là bổ đề đã có ở đây http://analgeomatica...1-thang-12.html

Từ đó đến bài của Bảo ta làm như sau

Gọi $U,V,W$ đối xứng $A,B,C$ qua $D,E,F$ thì $XU,YV,ZW$ đồng quy. Dễ thấy phép vị tự tâm $O$ tỷ số 3 biến đường thẳng qua trung điểm $AX$ và $D$ thành $XU$. Từ đó dễ thấy các đường thẳng mới đồng quy.

Đây là link gốc bài toán 60' 

http://www.artofprob...unity/c6h612592

$XK\parallel DS$ em suy ra $PSRD$ nội tiếp thế nào ? Đoạn đó nên giải thích kỹ hơn, vì $\angle RSC=\angle RCS=\angle RDP$. Sau khi có $X,K,N$ thẳng hàng thì ta có thể thấy $XY$ là trung trực $KL$ nên $XY$ là phân giác $\angle LXN$ kết hợp $YL=YN$ nên $XLYN$ nội tiếp.