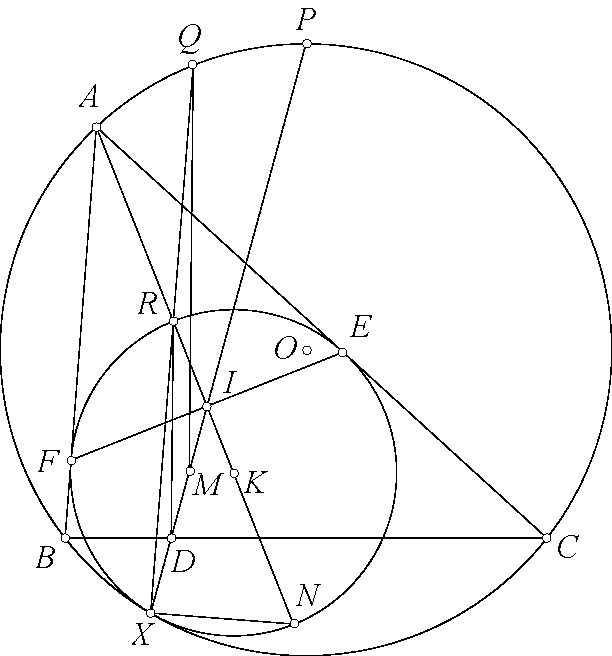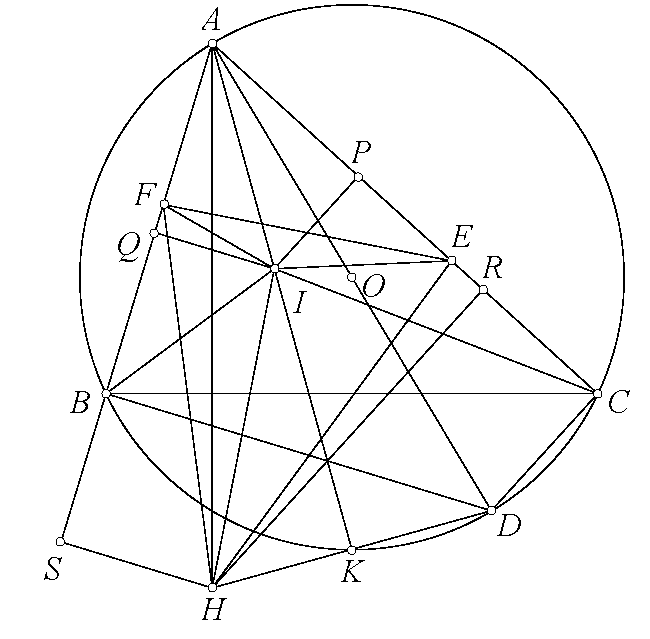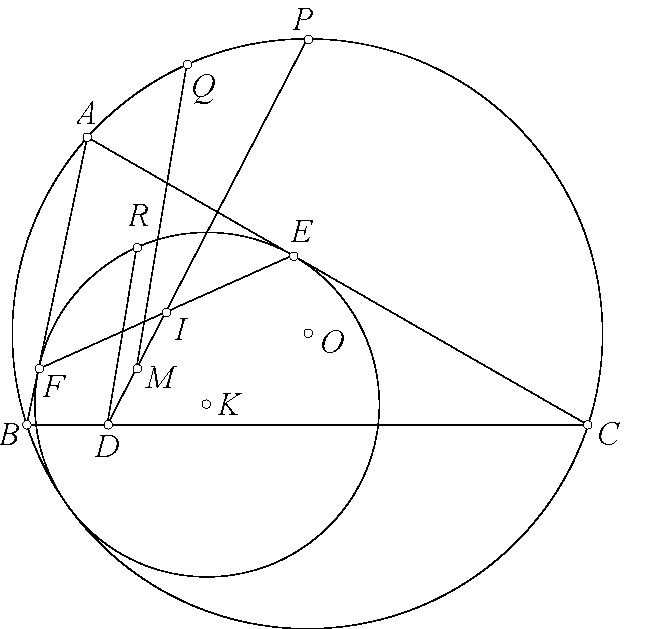Cám ơn Khánh và Quân, bài toán 123 là một bài không đơn giản, đáp án của thầy cũng tương tự của Khánh, lời giải của Quân khác của thầy, sau đây là đáp án bài toán 122.

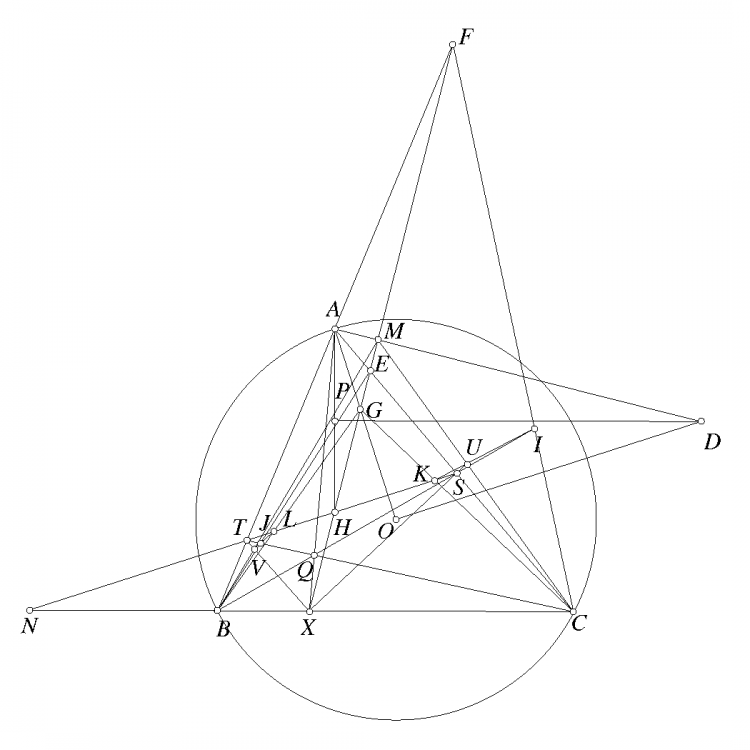
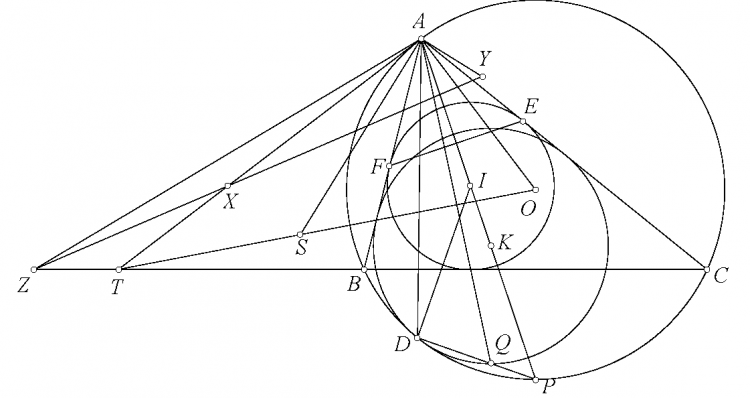
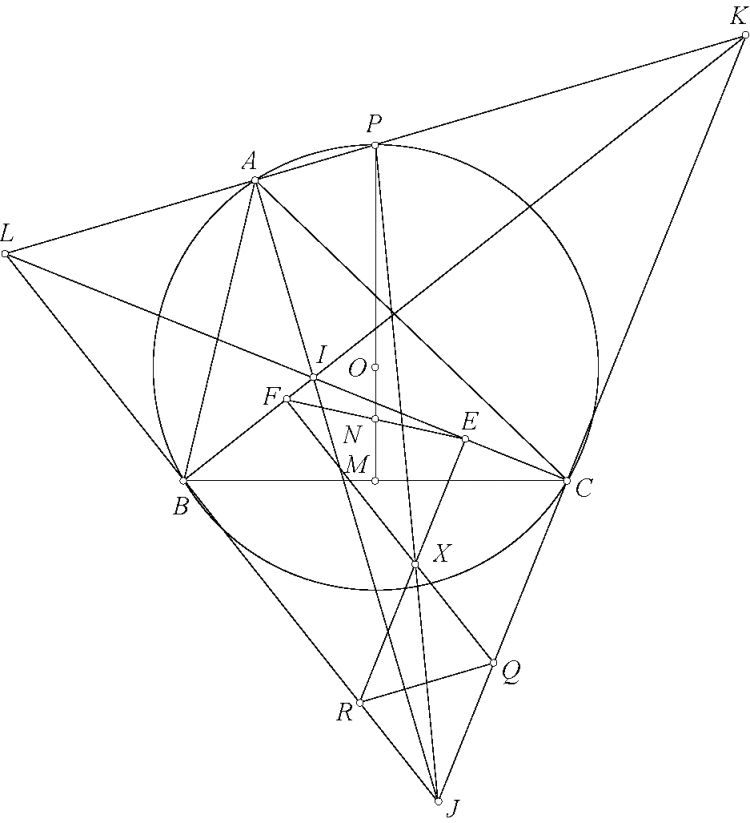
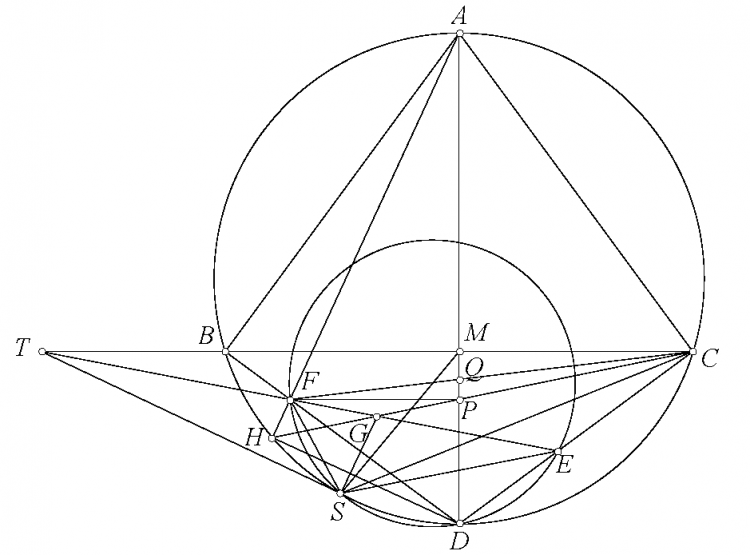
Đáp án bài toán 122. ta có $A(BC,OD)=-1$. Gọi $X$ là giao điểm $GH,BC$, $N$ là giao điểm $ST,BC$. Do $A(BC,OD)=-1$ và ta có $HC\perp AB, HB\perp AC, HN\perp OA, HM\perp AD$ suy ra $H(CB,NM)=-1$ suy ra $H(BC,XN)=-1$. Suy ra $BC,XN)=-1$ suy ra $AX,BS,CT$ đồng qui. Gọi điểm đồng qui của $AX,BS,CT$ là $Q$. Ta có $(GM,EF)=A(GM,EF)=A(OD,BC)=-1$ suy ra $B(TJ,LV)+(FE,GM)=-1$ và $C(SI,KU)=(EF,GM)=-1$. Mặt khác do $J,L,V$ thẳng hàng suy ra $T(BJ,VL)=B(TJ,VL)=-1$. Chứng minh tương tự suy ra $S(CI,UK)=1$ suy ra $T(BJ,VL)=S(CI,UK)=-1$ mà $TB,SC$ cắt nhau tại $A$, $TJ,SI$ cắt nhau tại $Q$ suy ra $AQ,TV,SU$ đồng qui. Cũng có $A(BJ,VL)=S(IC,UK)=-1$ mà $TB,SI$ cắt nhau tại $B$, $TJ,SC$ cắt nhau tại $C$, suy ra $SU,TV,BC$ đồng qui. Vậy $SU,TV,BC,AQ$ đồng qui. Mặt khác theo chứng minh trên thì $AQ,BC,GH$ đồng qui. Vậy $SU,TV,GH,BC$ đồng qui.

Thầy đề nghị bài mới cho topic tiếp tục

Bài toán 124. Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. Đường tròn nội tiếp $(I)$ tiếp xúc $CA,AB$ tại $E,F$. Đường tròn $(K)$ tiếp xúc $CA,AB$ và tiếp xúc trong $(O)$ tại $D$. $AI$ cắt $(O)$ tại $P$ khác $A$. $PD$ cắt $(K)$ tại $Q$ khác $D$. Tiếp tuyến tại $A$ của $(O)$ cắt $BC$ tại $T$, $OT$ cắt trung trực $AQ$ tại $S$. Lấy điểm $Y$ nằm trên đường nối trung điểm $AE,AF$ sao cho $AY\perp AS$. Tiếp tuyến tại $A$ của $(ADQ)$ cắt $BC$ tại $Z$. $AT$ cắt $YZ$ tại $X$. Chứng minh rằng $X$ là tâm $(ADI)$.

vietdohoangtk7nqd cần đề nghị bài tiếp nhưng vì lâu nên để bạn ấy đề nghị sau, để topic không bị gián đoán mình xin đề nghị bài tiếp

Bài toán 126 (AoPS). Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. $P$ nằm trên đường thẳng $OI$ của tam giác $ABC$. $X,Y,Z$ đối xứng $P$ qua $IA,IB,IC$. Chứng minh rằng $DX,EY,FZ$ đồng quy.

Cảm ơn Khánh về lời giải thú vị khác đáp án, đây là hình vẽ cho lời giải của em. Đáp án gốc thầy sẽ gõ và post vào hôm sau.

Mình đưa ra tổng quát bài toán 109 và lời giải của mình, nguồn gốc bài 109 là bài số 6 chọn đội Iran 2014 chứ không phải 2015

https://www.artofpro...h590555p3497371

Bài toán 109'. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ với tâm nội tiếp $I$ và tâm bàng tiếp góc $A$ là $J$. $P$ là trung điểm cung $BC$ chứa $A$ của $(O)$. $X$ thuộc $JP$. $E,F$ là hình chiếu của $X$ lên $IB,IC$. Chứng minh rằng $OP$ chia đôi $EF$.

Lời giải. Gọi $K,L$ là tâm bàng tiếp góc $B,C$ của $ABC$ thì $P$ là trung điểm $KL$. Gọi $XF,XE$ cắt $JC,JB$ tại $QR$. Dễ thấy do $XF\parallel JB$ và $XE\parallel JC$ nên $QR\parallel BC$. Từ đó $\frac{FB}{FK}=\frac{QJ}{QK}=\frac{RJ}{RL}=\frac{EC}{EL}$ nên theo bổ đề E.R.I.Q thì trung điểm của $KL,EF,BC$ thẳng hàng. Ta hoàn thành chứng minh.

Cách của thầy cũng giống hệt cách của Tuấn là tính hết ra và kết quả cuối cùng đúng như thế kia. Tuy nhiên Phước có cách giải thuần túy hình khá đẹp các bạn hãy cứ thử sức tiếp. Tuấn đề nghị một bài tiếp đi em!

Cám ơn em đã đăng lời giải, bài toán 150 có thể tham khảo lời giải dùng tỷ số kép ở đây.

Bài toán 151. Cho tam giác $ABC$ với đường cao $AD$. $E,F$ là hình chiếu của $D$ lên $CA,AB$. $EF$ cắt $BC$ tại $T$. $BE$ cắt $CF$ tại $S$. $K$ là tâm ngoại tiếp tam giác $SEF$. Một đường thẳng bất kỳ đi qua $T$ cắt $(ABC)$ tại $M,N$. Chứng minh rằng đường tròn có tâm trên $AK$ và đi qua $M,N$ thì tiếp xúc $(K)$.

Lời giải bài toán 165. Giả sử $\frac{AP}{AQ}=\frac{BP}{BQ}$. Gọi phân giác $\angle BAC$ cắt $PQ$ tại $I$ do thì $\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$ nên $BI$ là phân giác $\angle ABC$. Từ đó $I$ là tâm nội tiếp và $CI$ là phân giác $\angle ACB$ đồng thời cũng là phân giác $\angle PCQ$ nên $\frac{CP}{CQ}=\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$, ta hoàn thành chứng minh.

Mình có đôi lời. Vì sắp tới công việc của mình có nhiều biến chuyển nên mình chưa thể tập trung duy trì topic này liên tục đươc. Vậy mong những bạn yêu hình học có tâm huyết hãy đề nghị các bài toán hay có chất lượng để topic vẫn là sân chơi cho những bạn yêu thích hình học.

Lời giải bài toán 164. Gọi $AD$ là đường kính của $(O)$ ngoại tiếp $ABC$ thì $D,H$ đối xứng qua $K$. Từ đó gọi $P,Q$ là hình chiếu của $I$ lên $CA,AB$ và $R,S$ là hình chiếu của $H$ lên $CA,AB$ thì $AR=AB=c,AS=AC=b,AP=AQ=p-a,AF=p-b, AE=p-c$. Từ đó sử dụng tích vô hướng 2 vector.

$$\vec{IH}.\vec{EF}=\vec{IH}(\vec{AF}-\vec{AE})=QS.AF-PR.AE=(p-b)(c-(p-a))-(p-c)(b-(p-a))=0.$$

Nhận xét. Bài này có lẽ thu được từ bài quen thuộc từ việc lấy đối xứng trục.

Bài toán 165 (Crux). Cho tam giác $ABC$ có $P,Q$ là hai điểm đẳng giác. Giả sử hai trong ba tỷ số $\frac{AP}{AQ},\frac{BP}{BQ},\frac{CP}{CQ}$ bằng nhau. Chứng minh rằng cả ba tỷ số bằng nhau.

Cám ơn Hiếu, đúng là phần quan trọng nhất của bài toán này là từ bổ đề 2. Tuy nhiên việc phát biểu bài toán là từ một bài Iran trên AoPS, trong đó cũng có lời giải của Bảo. Em hãy đề nghị tiếp một bài toán cho topic được duy trì.

Bài toán 151 này là mở rộng của mình cho một bài toán của bạn Trịnh Huy Vũ, được post tại đây, xem #11, vẫn còn bài toán 146 chưa có lời giải, nếu tới mai không có ai giải mình sẽ post đáp án. Dark Repulsor em hãy đề nghị một bài toán tiếp.

Cám ơn Hoàng và Khánh, một lời giải khác cho bài toán 107 của thầy Hà ở đây, rất thú vị và ngắn gọn

https://www.artofpro...c6t48f6h1366405

Thầy giúp Hoàng đề nghị bài toán sau

Bài toán 111. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Đường tròn tâm nội tiếp $I$. Đường tròn $(K)$ tiếp xúc $CA,AB$ tại $E,F$ và tiếp xúc trong $(O)$. $P$ là trung điểm cung $BC$ chứa $A$ của $(O)$. $PI$ cắt $BC$ tại $D$. $Q$ là trung điểm cung nhỏ $AP$ của $(O)$. $R$ là trung điểm cung nhỏ $EF$ của $(K)$. $M$ là trung điểm $ID$. Chứng minh rằng $MQ\parallel DR$.

Lời giải sau do bạn Nguyễn Lê Phước gửi tới tác giả.

Lời giải bài toán 101. Gọi $NI$ cắt $HK$ tại $S$, $MI$ cắt $HL$ tại $T$ thì $S,T$ là tâm bàng tiếp tam giác $ANH,AMH$. Từ đó $\angle ASE=45^\circ=\angle AHL$ và $\angle AES=90^\circ+\angle ANE=\angle ALH$. Từ đó hai tam giác $ASE$ và $ALH$ đồng dạng g.g. Lại có $\angle ATH=90^\circ-\frac{\angle AMN}{2}=180^\circ-\angle AIN=\angle AIS$. Từ đó hai tam giác $ATH$ và $AIS$ đồng dạng g.g. Vậy $\frac{ES}{EI}=\frac{LH}{LT}$. Tương tự $\frac{FT}{FI}=\frac{KH}{KS}$. Từ đó $\frac{FI}{FT}.\frac{LT}{LH}=\frac{EI}{ES}.\frac{KS}{KH}$. Dùng định lý Menelaus dễ thấy $FL,ES$ cùng đi qua một điểm trên $IH$.

Lời giải khác của bạn Nguyễn Đức Bảo có thể xem tại http://artofproblems...1308940p7009306, bài toán này nằm trong chuỗi bài mở rộng bài toán IMO 2009 của tác giả http://analgeomatica...-2009-ngay.html

Bài toán 102 (Tập huấn đội IMO 2016). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định. $B$, $C$ cố định, $A$ di chuyển trên $(O)$. $I$ là tâm đường tròn nội tiếp tam giác $ABC$. $K$, $L$ theo thứ tự là trực tâm các tam giác $IAB$, $IAC$. $P$ đối xứng với $O$ qua trung điểm $KL$. Chứng minh rằng $AP$ đi qua một điểm cố định khi $A$ thay đổi.

Bài này phải dùng nhiều kỹ thuật, mặt khác vì nó là bài của mình tạo ra mình cũng không muốn đưa vào topic, vậy ta tạm gác lại, mình đề xuất một bài toán khác thay thế. 

$\boxed{\text{Bài toán 49.}}$ Cho tam giác $ABC$ và $P$ là điểm bất kỳ trong tam giác. Đường tròn $(K),(L)$ lần lượt ngoại tiếp các tam giác $PAC,PAB$ lần lượt cắt $BC$ tại $F,E$ khác $C,B$. $M$ là tâm ngoại tiếp tam giác $AEF$. $PA$ cắt $BC$ tại $D$. Trung trực $AD$ cắt đường thẳng qua $D$ vuông góc $BC$ tại $N$. $MN$ cắt $KL$ tại $Q$. Chứng minh rằng $Q$ nằm trên trung trực $BC$.

Mình nghĩ rằng nên có thêm một quy tắc, là những ai đề xuất bài vào topic này cần có đáp án, nếu bài không có đáp án chỉ nên thảo luận bên ngoài thôi.

Nguồn gốc của bài toán 57 là bài số 14 trong này http://geometry.ru/o...13/zaochn-e.pdf

Đáp án ở đây http://geometry.ru/o...13/zaochsol.pdf

Bài này là bài toán hay có nhiều phát triển và ứng dụng.

Cám ơn Bảo, lời giải của thầy
 

Topic hơi gián đoạn do bài toán 35 của Dương khá khó, tạm gác lại bài đó, mình xin đề xuất một bài tiếp như sau

$\boxed{\text{Bài toán 36.}}$ Cho tam giác $ABC$ cân tại $A$ nội tiếp đường tròn $(O)$ với $AD$ là đường kính của $(O)$. Các điểm $E,F$ lần lượt thuộc $DC,DB$. $G$ thuộc $EF$ sao cho $\frac{GF}{GE}=\frac{FB}{CE}$. Chứng minh rằng $CG$ và $AF$ cắt nhau trên $(O)$.

Khi đề xuất bài mình nghĩ nên có một số thứ tự các tiêu chí ưu tiên như sau

1) Đúng

2) Hay, đẹp

3) Mới

4) Sát với thi Olympic

5) Kiến thức đơn giản

6) Đề bài ngắn gọn, dễ hiểu

7) Nhiều hướng tiếp cận, tổng quát.

$\boxed{\text{Bài toán 71.}}$ Chứng minh rằng đường thẳng Simson của một điểm nằm trên đường tròn ngoại tiếp một tam giác chia đôi đoạn thẳng nối điểm đó và cực trực giao của đường thẳng Simson này với tam giác đã cho.

Dương đồng ý, mình xin đề nghị một bài khác

$\boxed{\text{Bài toán 73.}}$ Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$. $AD$ cắt $BC$ tại $E$. $AC$ cắt $BD$ tại $G$. $H$ là hình chiếu của $O$ lên $EG$. Trung trực $EH$ cắt $BC,AD$ tại $M,N$. Đường tròn $(HMB)$ và $(HNA)$ cắt nhau tại $K$ khác $H$. Chứng minh rằng $\triangle KBE\sim\triangle KEA$.

Cám ơn Quân(halloffame) đã nhắc mình chỉnh lại đề. Tiện thể mình thêm hình vẽ.

Đáp án bài toán 100.

Trong suốt bài toán này nếu $X$ là một điểm nằm trên đường tròn ngoại tiếp tam giác $ABC$ thì ta ký hiệu $s_X$ chỉ đường thẳng Simson của $X$ ứng với tam giác $ABC$. Ta sử dụng các bổ đề sau

Bổ đề 1. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $M,N$ thuộc $(O)$ thì $(s_M,s_N)=\frac{1}{2}(\overrightarrow{ON},\overrightarrow{OM})(\bmod\pi)$.
 

Bổ đề 2. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và trực tâm $H$ và $P$ là một điểm bất kỳ trên $(O)$ thì $s_P$ đi qua trung điểm $PH$.
 

Hai bổ đề là các bài toán cơ bản xin không nêu cách chứng minh.

Bổ đề 3. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $M,N$ là hai điểm thuộc $(O)$. $P$ là một điểm bất kỳ trên đường tròn đường kính $MN$. Gọi $m,n$ là hai đường thẳng lần lượt qua $M,N$ theo thứ tự song song với $s_M,s_N$. Khi đó thì đối xứng của $m,n$ lần lượt qua $PM,PN$ cắt nhau trên $(O)$.

Chứng minh. Bổ đề được chứng minh đơn giản bằng cộng góc. Thật vậy, gọi $m'$ và $n'$ lần lượt là đối xứng của $m,n$ qua $PM,PN$. Ta có biến đổi góc

$(m',n')=(m',PM)+(PM,PN)+(PN,n')(\bmod\pi)$

$=(PM,m)+(PN,PM)+(n,PN)(\bmod\pi)$ (Do $PM\perp PN$ nên $(PM,PN)=\frac{\pi}{2}=-\frac{\pi}{2}=(PN,PM)(\bmod\pi)$)

$=(n,m)(\bmod\pi)$

$=\frac{1}{2}(\overrightarrow{OM},\overrightarrow{ON})(\bmod\pi)$.

Ta chú ý $m'$ và $n'$ đi qua $M,N$ nên từ đó $m'$ và $n'$ cắt nhau trên $(O)$. Ta có điều phải chứng minh.

Giải bài toán.

Gọi $K',L'$ là ảnh của $K,L$ qua phép vị tự tâm $H$ tỷ số $2$. Vì $S$ cũng là ảnh của $T$ qua phép vị tự tâm $H$ tỷ số $2$ nên ta chỉ cần chứng minh $S$ là trung điểm của $K'L'$ thì bài toán được giải quyết. Thật vậy, theo bổ đề 2 dễ thấy phép vị tự tâm $H$ biết $s_M,s_N$ thành các đường thẳng $K'M,K'N$. Từ đó ta có $(K'M,K'N)=(s_M,s_N)=\frac{1}{2}(\overrightarrow{ON},\overrightarrow{OM})(\bmod\pi)$.

Vậy nếu gọi $R_1$ là đối xứng của $K'$ qua $MN$ thì $(R_1M,R_1N)=-(K'M,K'N)=\frac{1}{2}(\overrightarrow{OM},\overrightarrow{ON})(\bmod\pi)$ vậy suy ra $R_1$ thuộc $(O)$.

Tương tự nếu $R_2$ đối xứng $L'$ qua $PQ$ thì $R_2$ thuộc $(O)$.

Mặt khác từ việc lấy đối xứng ta có $R_1N,R_2P$ lần lượt là đối xứng của $NK',PL'$ theo thứ tự qua $SN,SP$. $S$ lại nằm trên đường tròn đường kính $NP$ vậy theo bổ đề 3 thì hai đường thẳng này phải có chung một điểm thuộc $(O)$. Vậy từ đó $R_1\equiv R_2\equiv R\in (O)$. Từ đó theo tính chất đối xứng trục, hai trục $MN,PQ$ vuông góc do đó $L'=\mathcal{R}_{PQ}(R)=\mathcal{R}_{PQ}[\mathcal{R}_{MN}(K')]=\mathcal{R}_{PQ}\circ \mathcal{R}_{MN}(K')=\mathcal{S}_{S}(K')$ vậy $K'$ và $L'$ đối xứng nhau qua $S$. Từ các nhận xét ban đầu ta thu được điều phải chứng minh.

Chuẩn rồi Bảo, cái điểm đồng quy của AX,BY,CZ đó gọi là điểm Prasolov đó. Điểm Prasolov nằm trên đường nối tâm Euler và điểm Lemoine !

Hệ quả đẹp của bài toán 86, hai tam giác $IAC,IBD$ có chung đường đối trung.

Đúng rồi cám ơn Dương, Bảo, điểm $K$ bị lặp, bài này là combine bài Turkey 2016 và CHKMO 2014 !

Ý chứng minh của Dương chính là bài CHKMO 2014 ở link. Mấu chốt là dựng ra tâm bàng tiếp $J$ vào sau đó chứng minh $H$ nằm trên $(JBC)$.

Nhân bài cũ của Bảo

Đễ xuất bài toán tiếp theo.

$\boxed{\text{Bài toán 77}}$ Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Giả sử $\triangle XYZ$ là tam giác tạo bởi các tiếp tuyến tại $A,B,C.AD,BE,CF$ lần lượt là đường kính của đường tròn $(O).P,Q,R$ theo thứ tự là trung điểm $AX,BY,CZ$. Chứng minh rằng $DP,EQ,FR$ đồng quy.

Nguồn

mjuk ~ Croatia

 

Thầy đề nghị thêm 1 ý là

b) Cmr đẳng giác của điểm đồng quy trong tam giác $DEF$ nằm trên đường thẳng Euler của tam giác $ABC$.

Nguồn gốc bài 9 http://www.artofprob...unity/c6h486466

Nguồn gốc bài 10 http://www.artofprob...unity/c6h470341