Để tiếp tục topic, xin đề nghị một bài toán mới.

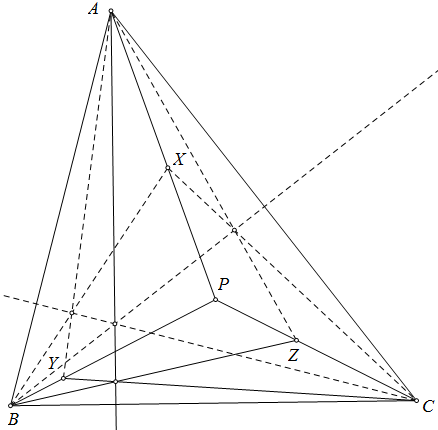
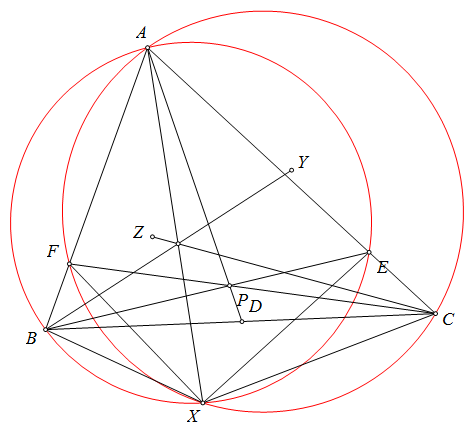
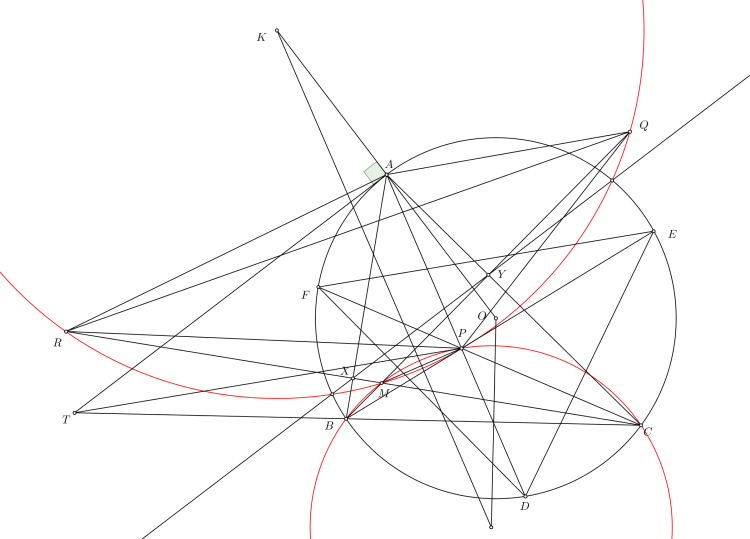
$\boxed{\text{Bài toán 72}}$ (Telv Cohl) Cho tam giác $ABC$ ngoại tiếp đường tròn tâm $I.(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F.P$ bất kì trong tam giác. $X,Y,Z$ lần lượt là giao điểm của $DP,EP,FP$ với $(I).X*,Y*,Z*$ lần lượt là giao điểm của $CY$ và $BX,AZ$ và $CX,AY$ và $BX$. 

Chứng minh rằng $XX*,YY*,ZZ*$ đồng quy tại $T$

Link gốc bài toán: http://www.artofprob...1240576p6333123

Đề xuất bài toán mới để tiếp tục topic.

$\boxed{\text{Bài toán 80}}$ (AoPS) Cho hình thang cân $ABCD$ nội tiếp đường tròn $\Omega$ với $AB\parallel CD.M$ là trung điểm $AB$ và $P$ là điểm chính giữa cung $CD$ không chứa $A$ của $\Omega$. Gọi $H$ là trực tâm tam giác $PAB$ và $(M)$ là đường tròn tâm $M$ đi qua $C,D.N$ là một điểm trên đoạn $AB$ ($N$ khác $A,B$ và $M$). Đường thẳng $HN$ cắt $(M)$ tại $K,L$ sao cho $L$ nằm trong $\Omega$. Chọn hai điểm $Q,R$ theo thứ tự thuộc $CD$ và $(M)$ sao cho $KQ,LR$ cùng vuông góc với $AB$. Gọi $RN$ cắt $CD$ tại $S$. Đường tròn ngoại tiếp tam giác $QRS$ cắt lại $(M)$ tại $E$. Chọn $F$ trên $ER$ sao cho $KF\perp KL$. Chứng minh rằng đường tròn ngoại tiếp tam giác $KEF$ tiếp xúc $\Omega$

Xin lỗi về sự trùng lặp, mình xin đề xuất lại một bài toán khác như sau.

$\boxed{\text{Bài toán 69}}$. Cho tam giác $ABC.P$ là một điểm bất kì trong tam giác $ABC.$ Trên $PA,PB,PC$ lần lượt lấy các điểm $X,Y,Z$ sao cho $AY,BX$, đường thẳng qua $C$ vuông góc $AB$ đồng quy, $AZ,CX$, đường thẳng qua $B$ vuông góc với $AC$ đồng quy. Chứng minh rằng $BZ,CY$, đường thẳng qua $A$ vuông góc $BC$ đồng quy.

Vừa mới chế ra, nếu trùng lặp ở đâu xin mọi người thứ lỗi!

Lời giải đầy đủ bài toán 67 có thể tham khảo link.

Theo đề nghị của anh Dogsteven mình xin đề xuất bài toán mới sau.

$\boxed{\text{Bài toán 68}}$ (AoPS) Cho tam giác $ABC$ với tâm đường tròn $Euler$ là $N.D,E,F$ là hình chiếu của $N$ lên $BC,CA,AB$. Chứng minh rằng đường thẳng $Euler$ của các tam giác $AEF,BFD,CDE,ABC$ đồng quy.

Theo yêu cầu của bạn Nguyen Dinh Hoang, xin đề xuất bài toán mới. 

$\boxed{\text{Bài toán 67}}$ (Trần Quang Hùng ~ Nguyễn Đức Bảo) Cho tam giác $ABC$. Một đường tròn $(K)$ qua $B,C$ cắt $CA,AB$ tại $E,F.H$ là giao điểm của $BE,CF$. Kẻ $HL\perp AK,LD\perp BC.M$ là trung điểm $BC.AK$ cắt $(CL)$ tại $N$. Đường thẳng qua $A$ song song với $CH$ cắt trung trực $AN$ tại $Q$

Chứng minh rằng $(Q,QA),(CL),(MD)$ đồng quy.

Mô hình bài toán này khá giống với một bài toán mình đề nghị trong topic, tất cả đều dựa trên mô hình bài toán ??? của thầy Trần Quang Hùng!

Nguồn gốc bài 66: http://www.artofprob...1108467p5035848

$\boxed{\text{Lời giải bài toán 82}}$. Bài này khá đơn giản!

Gọi $X,Y,Z$ lần lượt là giao điểm của $(AOX)(BOY)(COZ)$ với $(O)$. Do tứ giác $AOXD$ nội tiếp nên $\angle ADX=180^\circ-\angle AOX=2\angle OAX=2\angle ODX$. Từ đó $DA,DX$ đẳng giác trong $\angle BDC$. Chú ý tam giác $BDC$ đều nên từ đó $AD,AX$ đẳng giác trong $\angle A$. Theo định lí $Napoleon$ thì $AX,BY,CZ$ đồng quy tại điểm đẳng giác với điểm $Napoleon$ của tam giác $ABC$. Gọi điểm đó là $K$.

Gọi $OK$ cắt $(AOX)$ tại $T$ thì $OA^2=OK.OT$ từ đó $T$ xác định duy nhất trên $OK$. Mặt khác do $OA=OB=OC$ nên ba đường tròn $(AOX)(BOY)(COZ)$ đồng quy tại $T.\blacksquare$

PS. Kết quả về ba đường tròn đồng quy dạng này thì khá nhiều và quen thuộc với các chứng minh hoàn toàn tương tự như trên. 

Một kết quả khác như sau. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Gọi $X,Y,Z$ lần lượt là đối xứng của $A,B,C$ qua $BC,CA,AB$. Khi đó $(AOX)(BOY)(COZ)$ đồng quy.

Chứng minh hoàn toán tương tự như trên, chú ý điểm cần tìm ở đây là điểm $Konista$ của tam giác $ABC$.

Đề xuất bài toán tiếp theo khá nhẹ nhàng!

$\boxed{\text{Bài toán 83}}$.(AoPS) Cho tam giác $ABC$, trực tâm $H.M$ là trung điểm $BC$. Trên $BC$ lấy $S$ sao cho $HS,HM$ đẳng giác. Hạ $AP\perp HS$. Chứng minh rằng $(MSP)$ tiếp xúc $(ABC)$.

Đề xuất bài toán tiếp theo để tiếp tục topic!

$\boxed{\text{Bài toán 87}}$ (AoPS) Cho $\Omega$ và $\Omega'$ là các đường tròn cố định. $AA',BB'$ lần lượt là tiếp tuyến trong và tiếp tuyến ngoài của $\Omega$ và $\Omega'.C,C'$ là các điểm bất kì trên $\Omega,\Omega'$. Gọi $X,Y$ lần lượt là giao điểm của $AC$ và $A'C';BC$ và $B'C'$. Chứng minh rằng $(XY)$ luôn đi qua một điểm cố định khi $C,C'$ di chuyển.

Link lời giải bài toán 141 :  http://artofproblems...1341458p7284966

Lời giải bài 116.

Bổ đề. Cho tam giác $ABC$ nội tiếp đường tròn $O$, trực tâm $H$, $M$ là trung điểm $BC$. Đường cao $BE$, $CF$. $MH$ cắt $EF$ và $(O)$ lần lượt tại $R$, $K$. $KA$ cắt $MO$ tại $P$. Đường thẳng qua $P$ vuông góc với $EF$ cắt $KO$ tại $Q$. Khi đó $QR$ đi qua tâm đường tròn Euler của tam giác $ABC$.

Chứng minh. Do $AH\parallel PM$ nên $\tfrac{MH}{MK}=\tfrac{PA}{PK}=\tfrac{QO}{QK}$. Mặt khác do $(KHRM)=-1$ nên $\tfrac{MH}{MK}=\tfrac{RH}{RK}$. Từ đó theo định lí Menelaus $RQ$ đi qua trung điểm $OH$ hay $QR$ đi qua tâm đường tròn Euler của tam giác $ABC$. Bổ đề được chứng minh.

Quay lại bài toán.

Ta có $\widehat{QFB}=\widehat{QEF}=180^\circ-\widehat{QDF}=90^\circ-\tfrac{1}{2}\widehat{ABC}$ (do $DF$ đi qua điểm chính giữa cung $AB$ không chứa $C$ của $\triangle ABC$). Gọi $M$ là giao điểm của $QF$ với $BC$ thì $\triangle FBM$ cân tại $B$ suy ra $IF=IM=IE$ suy ra $I$ là tâm đường tròn ngoại tiếp tam giác $FME$ kéo theo $\widehat{EMF}=90^\circ$. Xác định điểm $N$ tương tự thì $\widehat{ENF}=90^\circ$. Do $\widehat{QDI}=90^\circ$ nên $DI$ đi qua điểm $Q'$ đối xứng với $Q$ qua $K$. Do đó $DI$ đi qua trực tâm tam giác $QEF$. Từ đó theo bổ đề ta có điều phải chứng minh.

Lời giải bài toán 115. Tiếp tuyến tại $A$ của $(O)$ cắt $BC$ tại $G$. Do tứ giác $ABXC$ điều hòa nên $GX$ tiếp xúc $(O)$, mặt khác do $(K)$ tiếp xúc $(O)$ tại $X$ nên $GX$ tiếp xúc $(K)$. Theo bài toán 112 thì $KS\perp BC$ nên $SY=SZ$. Do đó $GA^2=GX^2=GY\cdot GZ=\mathcal{P}_{G/(S)}=GS^2-SY^2$.

Theo định lý Cosin thì $GS^2=GO^2+OS^2-2OS.OG.\cos (\widehat{SOG})=GO^2+OS^2-\tfrac{1}{2}OL.OG.\cos (\widehat{SOG})$.

Gọi $T$ là giao điểm của $OG$ với $AX$. Do $OG\perp AX$ nên $OL.\cos(\widehat{SOG})=OT$, suy ra

$GS^2=GO^2+OS^2-\tfrac{1}{2}OG.OT=GO^2+OS^2-\tfrac{1}{2}R^2$

$\Rightarrow GA^2=GO^2-\tfrac{1}{2}R^2+OS^2-SY^2\Rightarrow SY^2-OS^2=\tfrac{1}{2}R^2$.

Gọi $F$ là giao điểm của $(XYE)$ với $AX$.

Ta có $LF\cdot LX=LY\cdot LE=SY^2-LS^2=SY^2-\tfrac{9}{16}LO^2=SY^2-OS^2-\tfrac{1}{2}OL^2=\tfrac{1}{2}(R^2-LO^2)=\tfrac{1}{2}LA\cdot LX$

$\Rightarrow F$ là trung điểm $AL$.$\square$

$\boxed{\text{Bài toán 96.}}$ (Telv Cohl) Cho tam giác $ABC$, $H$ là trực tâm. $M,N$ là các điểm trên $AB,AC$ sao cho $\angle HMB=\angle HNC=\alpha$.

Gọi $O$ là tâm đường tròn ngoại tiếp $\triangle HMN$. $D$ là điểm nằm cùng phía với $A$ đối với $BC$ sao cho $\angle DBC=\angle DCB=\alpha$.

Chứng minh rằng $H,O,D$ thẳng hàng.

Trâu bò vậy!

$\boxed{\text{Lời giải bài toán 57}}$

Áp dụng công thức đường trung tuyến ta chỉ cần chứng minh:

$MQ^2+NQ^2=MR^2+NR^2 \ (1)$

Theo bổ đề $Carnot$ thì $(1)\iff $

$\cos \angle QRM.MR=\cos \angle NQB.NQ$

$\iff \cos \angle ACD.MR=\cos \angle ABD.NQ$

$\iff sin \angle DAC.MR=\sin \angle ADB.NQ$

$P\equiv AC\cap BD$. Theo định lí $Sin$ thì

$\frac{\sin \angle DAP}{\sin \angle ADP}=\frac{PD}{PA}$

Ta cần chỉ ra

$\frac{NQ}{MR}=\frac{PD}{PA} \ (*)$

Tiếp tục sử dụng định lí $Sin$ và công thức diện tích ta suy ra

$\frac{MR}{MD}=\frac{\sin \angle MCB}{\sin \angle MCD}=\frac{PB.BC}{PD.CD}$

Tương tự thì 

$\frac{NQ}{NA}=\frac{PA.AB}{PC.BC}$

Mặt khác $MD=\frac{1}{2}AC \ , \ NA=\frac{1}{2}BD$ nên dễ suy ra $(*)$ đúng hay đẳng thức được chứng minh $\implies NQ=NR.\blacksquare$

Bài toán đề nghị. $\boxed{\text{Bài toán 58}}$ Cho tam giác $ABC$ nội tiếp $(O).I$ bất kì trên phân giác $\angle A.D,E,F$ lần lượt là hình chiếu của $I$ lên $BC,CA,AB.OI$ cắt $BC$ tại $K.L$ thuộc $AK$ sao cho $AI\parallel DL.LD$ cắt $EF$ tại $X$. Chứng minh rằng $X$ là trung điểm $DL$

Kết quả này mình từng mở rộng từ một bài tập của thầy mình, nếu có trùng lặp mong mọi người thông cảm! Bài toán gốc là khi $I\equiv $ tâm nội tiếp của tam giác $ABC$.

Nhân đề xuất bài toán mới, mình/em xin đưa ra một lời giải khác cho bài toán 54.

$\boxed{\text{Lời giải bài toán 54}}$ 

$E\equiv BQ\cap AC,F\equiv CQ\cap AB,X\equiv BH\cap AC,Y\equiv CH\cap AC$. 

Dễ thấy $QH$ là trục đẳng phương của $(BE)(CF)$. Gọi $M,N$ theo thứ tự là hình chiếu của $E,F$ lên $BA,AC$.

Dễ thấy $P\equiv XM\cap YN$. Mặt khác $M,N,X,Y$ đồng viên nên $PM.PX=PN.PY$ do đó $P$ thuộc trục đẳng phương của $(BE)(CF)$ hay $P,H,Q$ thẳng hàng.

$\boxed{\text{Bài toán 56}}$ (Thầy Trần Quang Hùng) Cho tam giác $ABC$ ngoại tiếp đường tròn tâm $I.(I)$ tiếp xúc $BC$ tại $D$. Trung trực $AD$ cắt $ID$ tại $M$. Gọi $E,F$ theo thứ tự là trung điểm $AD,AI$. Chứng minh rằng $OM$ chia đôi $EF$ với $(O)\equiv (ABC)$.

$\boxed{\text{Lời giải bài toán 7}}$

Ta cần có hai bổ đề sau:

$\boxed{\text{Bổ đề 1}}$ Cho tam giác $ABC$ có $O$ là tâm ngoại tiếp. Một đường tiếp tuyến với $\odot (BOC)$ cắt $AB$ ở $D$ và $CA$ ở $E$. Gọi $A'$ là điểm đối xứng của điểm $A$ qua $DE$. Khi đó $\odot (A'DE)$ tiếp xúc $\odot (ABC)$.

Chứng minh.

$\boxed{\text{Bổ đề 2}}$ Cho tam giác $IBC.Q,R$ lần lượt là trung điểm $IC,IB$. Kí hiệu $\omega $ là đường tròn $Euler$ của $\triangle IBC.PR,PQ$ cắt $\omega $ tại $F,E$. Khi đó tâm $\odot (PEF)$ thuộc $\omega $.

Chứng minh.

Quay lại bài toán.

Ta có $\angle IQP=90^\circ-\angle IMN+\angle AMK=90^\circ-\angle B/2+\angle C/2$. Tương tự $\angle IRP=90^\circ-\angle C/2+\angle B/2$.

Gọi $E,F$ lần lượt là giao của $PQ,PR$ với đường tròn $Euler$ của tam giác $IBC$. Theo bổ đề $2$ ta suy ra tâm $\odot (PEF)$ thuộc đường tròn $Euler$ của tam giác $IBC$. Theo bổ đề $1$ ta suy ra $\odot (PEF)$ tiếp xúc $\odot (XST).\blacksquare$

Bài toán đề nghị:

$\boxed{\text{Bài toán 8}}$ Cho hai đường tròn trực giao $(O_1),(O_2)$ cắt nhau tại $A,B.P$ bất kì trên $AB.O_1P$ cắt $\odot (O_2)$ tại $E.O_2P$ cắt $(O_1)$ tại $F.O_1O_2$ cắt $AB$ tại $D$. Chứng minh rằng $\frac {DE}{DF}=\frac{PE}{PF}$.

Nguồn.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 1\\ \hline IHateMath & 1\\ \hline fatcat12345 & 2\\ \hline dogsteven & 2\\ \hline baopbc & 3\\ \hline QuangDuong12011998 & 1\\ \hline\end{array}$$

$\boxed{\text{Lời giải bài toán 26}}$. Ta có $\angle HPM=\angle MNH=\angle MNA=\angle ACB\Longrightarrow P,X,H,C$ cùng thuộc một đường tròn 

$\Longrightarrow \angle PHX=\angle PCA$. Tương tự thì $\angle PHY=\angle PBA\Longrightarrow \angle PHX=\angle PHY\Longrightarrow H,X,Y$ thẳng hàng hay $XY$ đi qua $H.\blacksquare$

Hình vẽ bài toán

Bài toán đề nghị. $\boxed{\text{Bài toán 27}}$ (AopS) Cho tam giác $ABC,H$ là một điểm sao cho $\angle HBA=\angle HCA$. Trên đoạn $B,C$ lấy các điểm $D,E$ sao cho $\angle DHB=\angle EHC$. Trên $(ABC)$ lấy $K$ sao cho $\angle AKH=90^\circ$. Chứng minh rằng đường tròn ngoại tiếp tam giác $KDE$ tiếp xúc $(ABC)$.

Hình vẽ bài toán

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 3\\ \hline IHateMath & 1\\ \hline fatcat12345 & 3\\ \hline dogsteven & 4\\ \hline baopbc & 7\\ \hline QuangDuong12011998 & 2\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 2\\ \hline BuiBaAnh & 1\\ \hline halloffame & 1\\ \hline\end{array}$$

$\boxed{\text{Lời giải bài 5}}$ Gọi $X,Y,Z$ lần lượt là giao điểm thứ hai của $(ABE)$ và $(ACF),(BCF)$ và $(BAD),(CAD)$ và $(CBE)$

Hình vẽ bài toán

Ta có: $\frac{\sin \measuredangle XAB}{\sin \measuredangle XAC}=\frac{BX}{EX}$

Mặt khác $\triangle FXB\sim \triangle CXE$ nên $\frac {BX}{EX}=\frac{BF}{EC}\Longrightarrow \frac{\sin \measuredangle XAB}{\sin \measuredangle XAC}=\frac{BF}{EC}$. Tương tự với các cặp đường tròn còn lại

Theo định lí $Ceva$ dạng hình học thì $\frac{FA}{FB}.\frac{DB}{DC}.\frac{EC}{EA}$ nên theo định lí $Ceva$ dạng lượng giác thì $AX,BY,CZ$ đồng quy. $\blacksquare$

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 1\\ \hline IHateMath & 1\\ \hline fatcat12345 & 1\\ \hline dogsteven & 2\\ \hline baopbc & 2\\ \hline QuangDuong12011998 & 1\\ \hline\end{array}$$

Bài toán đề nghị. $\boxed{\text{Bài toán 6}}$ Cho tam giác $ABC$ nội tiếp $\odot (O)$ và $\odot (K)$ đi qua $B,C$ cắt $AC,AB$ tại $E,F.BE$ cắt $CF$ tại $H.\odot (AEF)$ cắt $\odot (O)$ tại $G$ khác $A.M,N$ lần lượt là tâm $\odot (GBK)$ và $\odot (GCK).FM$ cắt $EN$ tại $L$. Chứng minh $HL$ đi qua $O$.

Nguồn.

$\boxed{\text{Lời giải bài 3}}$. Để giải quyết bài toán ta cần có bổ đề sau:

Bổ đề. Cho $\triangle ABC$ nội tiếp $\odot (O).L$ là điểm $Lemoine.M$ là trung điểm $BC.AM$ cắt $(O)$ tại $N.NH$ vuông góc với $BC(H$ thuộc $BC).K$ đối xứng với $H$ qua $N.AL$ cắt $O$ tại $T$. Khi đó $LM\parallel KT$/

Chứng minh. Xem tại đây

Quay lại bài toán. $AL$ cắt $\odot (O)$ tại $T$.

Đường thẳng qua $T$ vuông góc với $TN$ cắt $BC,AM$ tại $X,Y$.

Hình vẽ bài toán

Do $AT,AN$ đẳng giác trong $\angle A$ nên $TNBC$ là hình thang cân $\Longrightarrow BX=CH\Longrightarrow MX=MH\Longrightarrow XM=\frac{TN}{2}$

$\Longrightarrow XT=\frac{YT}{2}$. Mặt khác theo bổ đề thì $XNKT$ là hình bình hành nên $NK=\frac{TY}{2}$.

$TK$ cắt $AM$ tại $Z\Longrightarrow K$ là trung điểm $ZT$ nên theo bổ đề hình thang ta suy ra $AK$ chia đôi $ML$.

Tiếp tục áp dụng bổ đề ta suy ra $K(RA,PF)=-1\Longrightarrow \overline{R,T,K}\Longrightarrow KR,AL$ cắt nhau tại một điểm thuộc $\odot (O).\blacksquare$

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 1\\ \hline IHateMath & 1\\ \hline fatcat12345 & 1\\ \hline dogsteven & 1\\ \hline baopbc & 1\\ \hline \end{array}$$

Bài toán đề nghị.$\boxed{\text{Bài toán 4}}$ (kết quả cũ) Cho tứ giác $ABCD$ nội tiếp $\odot (O).AC$ cắt $BD$ tại $R.AD$ cắt $BC$ tại $P$. Kẻ $RL\perp AD,PN\perp DR.Y$ là trung điểm $PR,X$ là trung điểm $CD$. Chứng minh $X,L,Y,N$ đồng viên.

$\boxed{\text{Bài toán 1}}$ Cho tam giác $ABC$ có $\angle A=60^\circ,\angle B=80^\circ$ nội tiếp $\odot (O)$, ngoại tiếp $\odot (I)$.

$AI$ cắt $OB$ tại $X$, cắt $BC$ tại $M$. Đường thẳng qua $C$ vuông góc với $AB$ cắt $OM$ tại $K$ và trung trực $BC$ tại $E.ME$ cắt $AC$ tại $L$. Đường thẳng qua $K$ vuông góc với $BC$ cắt $AC$ tại $F$. Chứng minh rằng $E,K,X,I,F,L$ cùng thuộc một đường tròn tâm $O$.

Nguồn.

Hình vẽ bài toán

Một cách khác cho bài 29, dài hơn một chút!

$\boxed{\text{Lời giải bài toán 29}}$ (Cách này có lẽ phù hợp với mấy đứa chưa học biến hình như em)

$\boxed{\text{Bổ đề 1}}$ Cho tam giác $ABC,L$ là điểm Miquel. $M$ là trung điểm $BC.$ Đường cao $AH$. Khi đó $ML$ chia đôi $AH$.

Bổ đề trên là bổ đề quen thuộc về điểm Lemoine, mình học từ anh viet nam in my heart, về chứng minh mọi người có thể nhắn tin qua anh viet nam in my heart hoặc đọc trong các tài liệu về điểm Lemoine.

Giải bài toán. (Có lẽ vẫn cần tính toán nhưng không dài như anh Ngockhanh99k48)

Dễ thấy chỉ cần chứng minh $AA'$ đi qua trung điểm $OL$.

$T\equiv AD\cap OA'$. Theo tính chất quen thuộc, dễ thấy $(AD,LT)=-1.N,P$ theo thứ tự là trung điểm $AH,AD$. Do $AFDE$ là hình bình hành nên $P$ là trung điểm $EF\Longrightarrow A'P\perp EF\Longrightarrow AO\parallel A'P$. Áp dụng bổ đề 1 ta suy ra $M,L,N$ thẳng hàng. Mặt khác do $(AD,LT)=-1$ nên theo định lí Thales ta suy ra $A'D\parallel OL$. Mặt khác $A'(DA,LO)=-1\Longrightarrow AA'$ đi qua trung điểm $OL.\blacksquare$

Bài này không cần tính điểm đâu nhé! Anh viet nam in my heart đề xuất bài mới đi!

$\boxed{\text{Lời giải bài toán 33}}$. Theo lời giải $\boxed{\text{Bài toán 1}}$ của anh Ngockhanhk9948 thì $\angle OMA=40^\circ$.

Mặt khác $\angle AMB=180^\circ-80^\circ-30^\circ=70^\circ\Longrightarrow \angle OMC=70^\circ\Longrightarrow \angle OKF=20^\circ$.

Lại có $\angle AOM=180^\circ-\angle MAO-\angle OMA=180^\circ-20^\circ-40^\circ=120^\circ$. Mà theo lời giải $\boxed{\text{Bài toán 1}}$ của anh dogsteven thì $\angle AOI=60^\circ\Longrightarrow \angle KOI=60^\circ$ hay $\triangle OIK$ đều.

Đường thẳng qua $K$ vuông góc với $OI$ cắt $OF$ tại $T$. Dễ thấy $\angle FKT=\angle 30^\circ-20^\circ=10^\circ\Longrightarrow \triangle TFK$ cân tại $F$ hay $T$ thuộc $(F,FK)$. Mặt khác theo lời giải $\boxed{\text{Bài toán 1}}$ của anh I Hate Math thì $\angle OSK=20^\circ$ với $S$ là điểm chính giữa cung $BC$ không chứa $A$ nên $T$ thuộc $(O)$. Mặt khác $T,F,O$ thẳng hàng nên $(F,FK)$ tiếp xúc $(O).\blacksquare$.

P/s.

Sao không ai giải cả vậy! Mọi người cùng quẩy cho topic sôi nổi đi chứ

Bài toán đề nghị. $\boxed{\text{Bài toán 34}}$. (AopS). Cho hình thang cân $ABCD$ nội tiếp $(O).DO$ cắt $BC$ tại $X$. Đường thẳng qua $X$ song song với $OA$ cắt $AB,AC$ theo thứ tự tại $E,F.(O')\equiv (DEF)$. Tiếp tuyến tại $A$ của $(O)$ cắt $(O')$ tại $P,Q$. Chứng minh rằng $(O'PQ)$ tiếp xúc $(O)$.

$\textbf{Hình vẽ bài toán}$

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 6\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 8\\ \hline QuangDuong12011998 & 3\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

$\boxed{\text{Lời giải bài toán 55}}$ (Tóm tắt)

$M\equiv CR\cap BQ$. Đế ý $\triangle CAR\sim \triangle EOD,\triangle BAQ\sim \triangle FOD$ dễ suy ra $\angle BMY=\angle BPC\implies B,M,P,C$ đồng viên.

Theo kết quả quen thuộc thì $DE=DF$ từ đó $\triangle CAR\sim \triangle BAQ$

Đế ý $\frac{PB}{PC}=\frac{AB}{AC}\implies \frac{PB}{BQ}=\frac{PC}{PR}\implies \triangle RPC\sim \triangle QPB$

$\implies R,Q,P,M$ đồng viên.

$X\equiv CM\cap AB,Y\equiv BM\cap AC$. Đế ý $\angle ACR=\angle ABQ$ nên $B,X,Y,C$ đồng viên $\implies XY\perp AO$

Đế ý $\angle ABM=\angle ACR=\angle ARC\implies A,R,B,M$ đồng viên $\implies XR.XM=XB.XA\implies X$ thuộc trục đẳng phương của $(O)$ và $(PQR)$.

Tương tự kéo theo $XY$ là trục đẳng phương của $(O)$ và $(PQR)\implies XY\perp OK\implies A,O,K$ thẳng hàng.$\blacksquare$

$\boxed{\text{Lời giải bài toán 44}}$ Bài gốc hay bài tổng quát đều không khó, lời giải của em dựa trên lời giải bài gốc mà em đưa lên trong link!

Do $P$ thuộc trung trực $BC$ nên $\angle QCA=\angle QBA\implies AE=AB,AF=AC\implies \triangle ABF=\triangle AEC$

$\implies BF=CE$. Mặt khác dễ thấy $\angle ECD=\angle DBF$ nên $\triangle DCE=\triangle DBF\implies DE=DF,\angle EDF=\angle BDC$

$\implies \angle EFD=\angle CBD.S\equiv DB\cap (DEF)$. Do $\angle BSE=\angle DFE=\angle DBC$ nên $BC\parallel SE$

Mặt khác dễ thấy $\angle BAE=2\angle DBC=2\angle BSE$ nên $A$ là tâm ngoại tiếp tam giác $BES\implies AK\perp SE\implies AK\perp BC.\blacksquare$

Ủng hộ câu a, trước. Câu b, chắc để sau vậy!

$\boxed{\text{Lời giải bài toán 43a}}$ Ta sẽ sử dụng bổ đề $Ceva$ trong đường tròn.

Cho tam giác $ABC$ nội tiếp $(O)$, các điểm $A',B',C'$ nằm trên $(O)$. Khi đó $AA',BB',CC'$ đồng quy $\Longleftrightarrow \frac{A'B}{A'C}.\frac{B'C}{B'A}.\frac{C'A}{C'B}=1$

Quay lại bài toán: Biến đổi tỉ số đơn giản $\frac{\sin \angle P_aAE}{\sin \angle P_aAF}=\frac{P_aE^2}{P_aF^2}$

Tương tự và áp dụng bổ đề trên ta suy ra $\frac{\sin \angle P_aAE}{\sin \angle P_aAF}.\frac{\sin \angle P_bBF}{\sin \angle P_bBD}.\frac{\sin \angle P_cCD}{\sin \angle P_cCE}=1$

Theo định lí $Ceva$ dạng lượng giác suy ra $AP_a,BP_b,CP_c$ đồng quy. $\blacksquare$

PS. Anh Khánh ghi nguồn đầy đủ đi chứ?

$\boxed{\text{Lời giải bài toán 36}}$ (Bài này chắc phải dùng chút lượng giác quá! )

$X\equiv AE\cap (O),Y\equiv AF\cap (O),G'\equiv BX\cap CY$. Theo định lí $Pascal$ thì $G'$ thuộc $EF$.

Ta có biến đổi tỉ số $\frac{FB}{EC}=\frac{\sin \angle BAY.AF}{\sin \angle CAX.AE}=\frac{\sin \angle G'CB.AF}{\sin \angle G'BC.AE}=\frac{G'B.AF}{G'C.AE}$

$K\equiv AX\cap CY,L\equiv AY\cap BX$. Do tam giác $ABC$ cân tại $A$ nên $LKXY$ là tứ giác nội tiếp $\Rightarrow LK\parallel BC$

Theo định lí $Thales$ thì $\frac{G'B}{G'C}=\frac{G'L}{G'K}$. Áp dụng định lí $Sin$ cho các tam giác $G'LF$ và $G'KE$ ta được:

$\frac{G'F}{G'E}=\frac{G'L.\sin \angle G'LF.\sin \angle AFE}{G'K.\sin \angle G'KE.\sin \angle AEF}=\frac{G'B.\sin \angle AFE}{G'C.\sin \angle AEF}=\frac{G'B.AF}{G'C.AE}=\frac{FB}{EC}\Rightarrow G\equiv G'$ hay $AF,CG$ cắt nhau trên $(O).\blacksquare$

Hình vẽ bài toán

Bài toán đề nghị. $\boxed{\text{Bài toán 37}}$ (Romani TST 2016 Day 4 Problem 2) Cho tam giác $ABC,CA\neq CB.D,F,G$ theo thứ tự là trung điểm $AB,AC,BC$. Một đường tròn $\gamma $ qua $C$, tiếp xúc với $AB$ tại $D$ và cắt $AF,BG$ lần lượt tại $H,I.H',I'$ lần lượt đối xứng với $H,I$ qua $F,G.H'I'$ cắt $CD$ và $FG$ lần lượt tại $Q,M$ và $CM$ cắt $\gamma $ tại $P$. Chứng minh rằng $\triangle CPQ$ cân.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 6\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 9\\ \hline QuangDuong12011998 & 4\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

Chào các thành viên của VMF!

Thay cho lời mở đầu mọi người hãy đọc qua topic sau.

Marathon Số học đã được anh Ego bắt đầu, vì vậy mình xin bắt đầu cuộc thi Marathon Hình học!

Các quy định đã được đề cập rõ tại đây.

Để tăng tính thẩm mĩ mọi người có thể làm theo code sau: