Cám ơn Bảo, quá nhanh và nguy hiểm , thầy đề nghị bài tiếp.

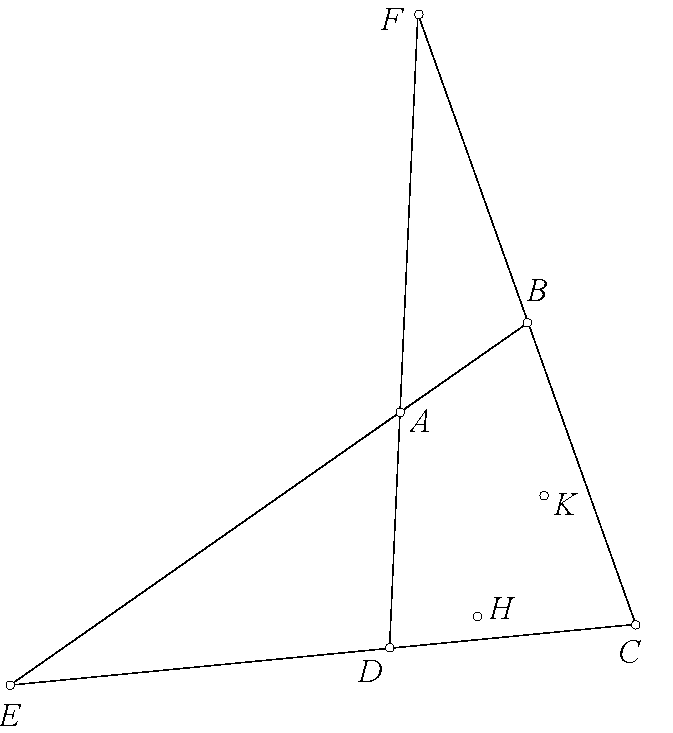
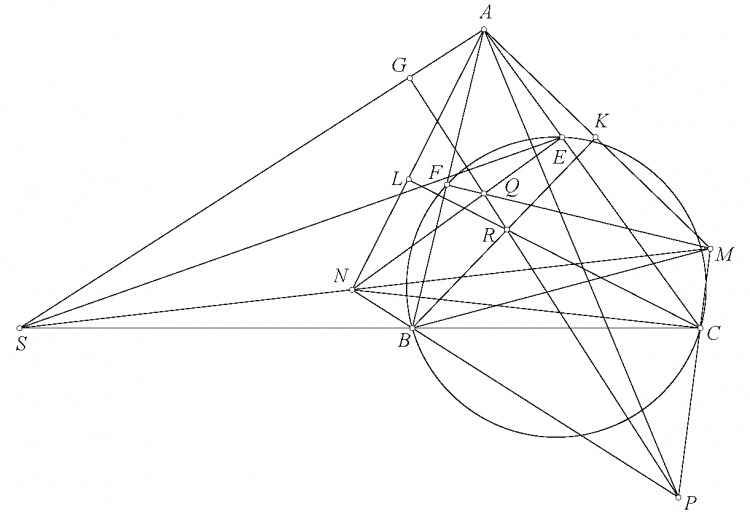
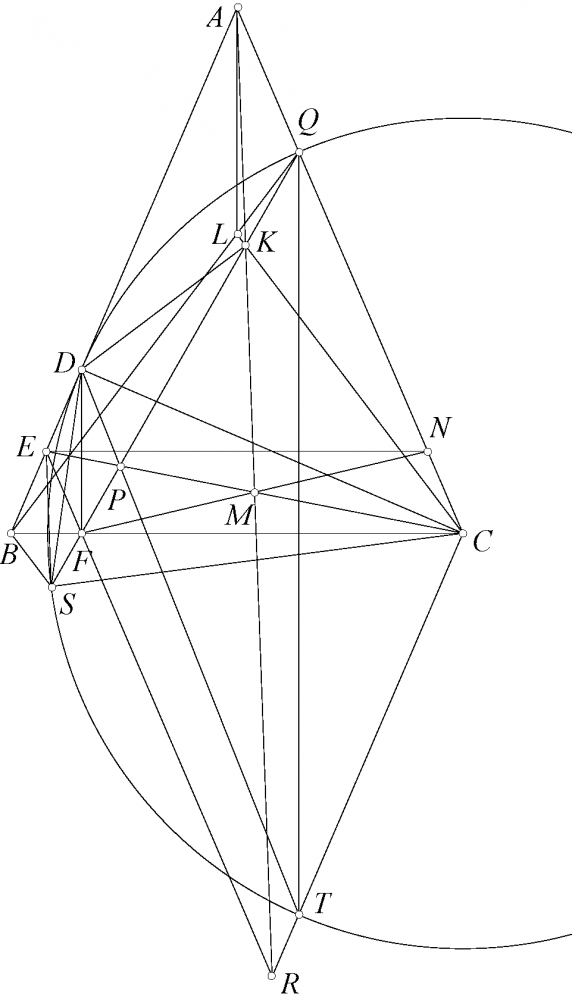
Bài toán 122. Cho tam giác $ABC$, trực tâm $H$, tâm ngoại tiếp $O$. Đường thẳng qua $O$ vuông góc $OA$ cắt trung trực $AH$ tại $D$. $M$ là hình chiếu của $H$ lên $AD$. $HM$ lần lượt cắt $CA,AB,OA$ tại $E,F,G$. đường thẳng qua $H$ song song $OD$ cắt $CA,AB,GC,GB$ lần lượt tại $S,T,K,L$. $SB,TC$ lần lượt cắt $CF,BE$ tại $I,J$. $IK,JL$ lần lượt cắt $MC,MB$ tại $U,V$. Chứng minh rằng $SU,TV,GH,BC$ đồng qui.

Cám ơn em đã đóng góp xây dựng, mọi đóng góp ở mức độ nào đều là đáng trân trọng. Ai cũng phải học hỏi vì kiến thức là vô hạn kể cả trong nội tại hình học sơ cấp, thầy cũng phải luôn học tập và cố gắng hơn.

Nói qua về bài tập này http://artofproblems...c6t48f6h1368124, mình có 1 phát hiện nhỏ, nếu định nghĩa các điểm $Y,Z$ tương tự thì $IX=IY=IZ$ nói cách khác ta có thể chứng minh được $AX,BY,CZ$ đồng quy.

Cám ơn Bảo vì lời giải rất nhanh và đẹp, theo đề nghị của em thầy để xuất tiếp bài sau

Bài toán 117. Cho lục giác lồi $ABCDEF$ thỏa mãn $AB=CD=EF$, $BC=DE=FA$ và $\angle A+\angle B=\angle C+\angle D=\angle E+\angle F$. Chứng minh rằng $\angle A=\angle C=\angle E$.

Bài toán 114 của bạn NHN có nhiều phát triển thú vị, mọi người hãy cùng quan tâm.

Cám ơn Khánh đã giải và gửi bài mới, bài toán của thầy Hà quả thật rất thú vị. Mình xin đưa ra lời giải của mình như sau.

Ta chú ý rằng có một tính chất quen thuộc từ cấu hình trên là $BP=CQ=r$ là bán kính nội tiếp tam giác $ABC$. Do đó để đẹp hơn ta nên phát biểu như sau

Bài toán 107'. Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc với $CA,AB$ tại $E,F$. $P,Q$ đối xứng với $I$ lần lượt qua trung điểm $BE,CF$. $PQ$ cắt $EF$ tại $R$. Chứng minh rằng $IR\parallel BC$.

Lời giải. Gọi $IB,IC$ cắt $EF$ tại $M,N$ dễ thấy $M,N$ nằm trên đường tròn đường kính $BC$. Gọi $BK,CL$ là đường cao của tam giác $ABC$. Ta thấy $FQ\parallel CN$ nên $\angle QFM=\angle CNM=\angle CBM=\angle CLM$. Từ đó tứ giác $FMQL$ nội tiếp nên $QM\perp MN$. Tương tự $PN\perp MN$. Từ biến đổi góc trên dễ thấy hai tam giác vuông $MFQ$ và $MBC$ đồng dạng suy ra hai tam giác $MFB$ và $MQC$ đồng dạng. Tương tự hai tam giác $NEC$ và $NPB$ đồng dạng. Ta thu được $\frac{RN}{RM}=\frac{NP}{MQ}=\frac{NP}{BP}.\frac{CQ}{MQ}=\frac{NE}{EC}.\frac{BF}{FM}=\frac{IN}{IM}.\frac{IN}{IM}$, ta chú ý đẳng thức cuối có do các tứ giác $INFB$ và $IEMC$ nội tiếp. Vậy $\frac{RN}{RM}=\frac{IN^2}{IM^2}$ nên $IR$ tiếp xúc $(IMN)$ do đó $\angle RIN=\angle IMN=\angle ICB$. Từ đó $IR\parallel BC$.

Bài toán 108 (Mở rộng ý a) bài toán 7 VMO 2017). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Một đường tròn $(K)$ đi qua $B,C$. Trung trực $BC$ cắt $(K)$ tại $M,N$. $P$ là điểm thuộc $(K)$. $PM$ cắt $CA,AB$ tại $E,F$. $BE$ cắt $CF$ tại $L$. Chứng minh rằng $AL,PN$ và $BC$ đồng quy.

Đáp án bài toán 100.

Trong suốt bài toán này nếu $X$ là một điểm nằm trên đường tròn ngoại tiếp tam giác $ABC$ thì ta ký hiệu $s_X$ chỉ đường thẳng Simson của $X$ ứng với tam giác $ABC$. Ta sử dụng các bổ đề sau

Bổ đề 1. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $M,N$ thuộc $(O)$ thì $(s_M,s_N)=\frac{1}{2}(\overrightarrow{ON},\overrightarrow{OM})(\bmod\pi)$.
 

Bổ đề 2. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và trực tâm $H$ và $P$ là một điểm bất kỳ trên $(O)$ thì $s_P$ đi qua trung điểm $PH$.
 

Hai bổ đề là các bài toán cơ bản xin không nêu cách chứng minh.

Bổ đề 3. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $M,N$ là hai điểm thuộc $(O)$. $P$ là một điểm bất kỳ trên đường tròn đường kính $MN$. Gọi $m,n$ là hai đường thẳng lần lượt qua $M,N$ theo thứ tự song song với $s_M,s_N$. Khi đó thì đối xứng của $m,n$ lần lượt qua $PM,PN$ cắt nhau trên $(O)$.

Chứng minh. Bổ đề được chứng minh đơn giản bằng cộng góc. Thật vậy, gọi $m'$ và $n'$ lần lượt là đối xứng của $m,n$ qua $PM,PN$. Ta có biến đổi góc

$(m',n')=(m',PM)+(PM,PN)+(PN,n')(\bmod\pi)$

$=(PM,m)+(PN,PM)+(n,PN)(\bmod\pi)$ (Do $PM\perp PN$ nên $(PM,PN)=\frac{\pi}{2}=-\frac{\pi}{2}=(PN,PM)(\bmod\pi)$)

$=(n,m)(\bmod\pi)$

$=\frac{1}{2}(\overrightarrow{OM},\overrightarrow{ON})(\bmod\pi)$.

Ta chú ý $m'$ và $n'$ đi qua $M,N$ nên từ đó $m'$ và $n'$ cắt nhau trên $(O)$. Ta có điều phải chứng minh.

Giải bài toán.

Gọi $K',L'$ là ảnh của $K,L$ qua phép vị tự tâm $H$ tỷ số $2$. Vì $S$ cũng là ảnh của $T$ qua phép vị tự tâm $H$ tỷ số $2$ nên ta chỉ cần chứng minh $S$ là trung điểm của $K'L'$ thì bài toán được giải quyết. Thật vậy, theo bổ đề 2 dễ thấy phép vị tự tâm $H$ biết $s_M,s_N$ thành các đường thẳng $K'M,K'N$. Từ đó ta có $(K'M,K'N)=(s_M,s_N)=\frac{1}{2}(\overrightarrow{ON},\overrightarrow{OM})(\bmod\pi)$.

Vậy nếu gọi $R_1$ là đối xứng của $K'$ qua $MN$ thì $(R_1M,R_1N)=-(K'M,K'N)=\frac{1}{2}(\overrightarrow{OM},\overrightarrow{ON})(\bmod\pi)$ vậy suy ra $R_1$ thuộc $(O)$.

Tương tự nếu $R_2$ đối xứng $L'$ qua $PQ$ thì $R_2$ thuộc $(O)$.

Mặt khác từ việc lấy đối xứng ta có $R_1N,R_2P$ lần lượt là đối xứng của $NK',PL'$ theo thứ tự qua $SN,SP$. $S$ lại nằm trên đường tròn đường kính $NP$ vậy theo bổ đề 3 thì hai đường thẳng này phải có chung một điểm thuộc $(O)$. Vậy từ đó $R_1\equiv R_2\equiv R\in (O)$. Từ đó theo tính chất đối xứng trục, hai trục $MN,PQ$ vuông góc do đó $L'=\mathcal{R}_{PQ}(R)=\mathcal{R}_{PQ}[\mathcal{R}_{MN}(K')]=\mathcal{R}_{PQ}\circ \mathcal{R}_{MN}(K')=\mathcal{S}_{S}(K')$ vậy $K'$ và $L'$ đối xứng nhau qua $S$. Từ các nhận xét ban đầu ta thu được điều phải chứng minh.

Cám ơn các em đã đóng góp.

Đáp án bài 125. Dựng đường tròn $(B)$ tiếp xúc $AC$. Các tiếp tuyến tại $C,A$ của $(B)$ cắt nhau tại $F$. Từ dữ kiện đề bài dễ thấy hai tam giác $\triangle EDA=\triangle BCF$ g.c.g. Từ đó $EA=BF$ mà $BE\parallel AF$ nên tứ giác $BEAF$ có thể là một hình thang cân hoặc hình bình hành. Nhưng $\angle AEB<\angle AED=\angle CBF<\angle EBF$ do đó $BEAF$ là một hình bình hành. Dễ suy ra $BCDE$ là hình bình hành.

Bài toán 134 là một mở rộng của bài chọn đội tuyển Mỹ mình đã post ở đây trong #11 và các lời giải ở #12,#13 và #15.

Ta xét một bài toán tổng quát hơn của bài toán 135, có thể coi là bổ đề.

Bài toán 135'. Cho tam giác $ABC$ và $P$ nằm trong tam giác. $PA,PB,PC$ cắt $(O)$ tại $D,E,F$. $X,Y,Z$ đối xứng $D,E,F$ qua trung điểm $BC,CA,AB$. Chứng minh rằng $(XYZ)$ đi qua trực tâm $H$ của $ABC$.

Giải. Vì $D,X$ đối xứng qua trung điểm $BC$ nên hai tam giác $ABC$ và $ADX$ có chung trung tuyến hay có chung trọng tâm $G$. Từ đó $X$ là ảnh vị tự trung điểm $U$ của $AD$ qua phép vị tự tâm $G$ tỷ số $-2$. Tương tự $Y,Z$ là ảnh vị tự tâm $G$ tỷ số $-2$ của $V,W$ lần lượt là trung điểm của $BE,CF$. Dễ thấy $O,U,V,W$ nằm trên đường tròn đường kính $OP$ nên $(XYZ)$ đi qua ảnh vị tự của $O$ trong qua phép vị tự tâm $G$ tỷ số $-2$ chính là $H$. Ta hoàn tất chứng minh,

Trở lại bài toán 135. Ta chỉ cần $P$ di chuyển trên một đường thẳng cố định đi qua $A$. Gọi đường thẳng đó cắt $(O)$ tại $L$ thì đường tròn $(HRS)$ luôn đi qua đối xứng của $L$ qua trung điểm $BC$ cố định nên tâm của $(HRS)$ thuộc một đường thẳng cố định.

Mình xin đề nghị bài tiếp.

Bài toán 136. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ đường tròn bàng tiếp góc $A$ là $(J)$ tiếp xúc $BC$ tại $D$. Đường tròn qua $A,B$ tiếp xúc $(J)$ tại $M$. Đường tròn qua $A,C$ tiếp xúc $(J)$ tại $N$. $BM$ cắt $CN$ tại $P$. Chứng minh rằng $\angle PAB=\angle DAC$.

Lời giải bài toán 160.

Bổ đề. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ tâm nội tiếp $I$. $IB,IC$ cắt $(O)$ tại $P,Q$. Gọi $(P)$ là đường tròn tâm $P$ tiếp xúc $AC$. Gọi $(Q)$ là đường tròn tâm $Q$ tiếp xúc $AB$. Chứng minh rằng có một tiếp tuyến chung của $(P),(Q)$ đi qua $I$.

Chứng minh. Vẽ $AX$ tiếp xúc $(P)$ thì $\angle XAC=2\angle PAC=2\angle PBC=\angle ABC$. Từ đó $AX$ là tiếp tuyến của $(O)$. Tương tự $AY$ tiếp xúc $(Q)$ thì $AY$ là tiếp tuyến của $(O)$ nên $X,Y,A$ thẳng hàng. Vậy tiếp tuyến chung ngoài của $(P),(Q)$ đi qua $A$. Qua đối xứng trục $PQ$ thì tiếp tuyến chung ngoài còn lại đi qua $I$.

Giải bài toán. Dễ thấy tâm $X$ của đường tròn nội tiếp tam giác $AEF$ là trung điểm cung $EF$ của $(I)$. Tương tự với các đường tròn $(Y),(Z)$. Do đó theo bổ đề thì tiếp tuyến chung ngoài khác $BC$ của $(Y),(Z)$ đi qua tâm $J$ nội tiếp tam giác $DEF$. Tương tự với các tiếp tuyến chung của $(Z),(X)$ và $(X),(Y)$. Dễ thấy do $J$ là tâm nội tiếp $DEF$ và $I$ là tâm ngoại tiếp $DEF$ nên đường thẳng $IJ$ là đường thẳng Euler của tam giác pedal của $J$ với $DEF$ nên $IJ$ đi qua $G$ là trọng tâm của tam giác pedal của $J$.

Bổ đề này thực chất là bài toán vô địch Nga năm nào đó, kết quả bài toán 160 cũng đã có trên AoPS.

Bài toán 163 (AoPS). Cho tam giác $ABC$ với tâm nội tiếp $I$ và $P$ thỏa mãn $\angle PIA=90^{\circ}$. $Q$ là đẳng giác của $P$ với $ABC$. $D$ thuộc $BC$ sao cho $PD\parallel AQ$. Chứng minh rằng đường tròn đường kính $\odot(AP)$ tiếp xúc đường tròn đường kính $\odot(QD)$. 

Bài toán 148 có thể tham khảo tại đây trong #4 của Telv Cohl.

Lời giải bài toán 149.

Sử dụng định lý Desargues thì bài toán cần chứng minh tương đương với giao điểm của các cặp đường thẳng $(B_cC_b,BC);(C_aA_c,AC);(A_bB_a,AB)$ thẳng hàng khi và chỉ khi giao điểm của $(A_bA_c,BC);(B_cB_a,AC);(C_aC_b,AB)$ thẳng hàng, Gọi $B_cC_b$ và $A_bA_c$ cắt $BC$ lần lượt tại $A_3,A_4$ thì áp dụng định lý Menelaus ta thấy $\frac{A_3B}{A_3C}=\frac{B_cP}{B_cC}.\frac{C_bB}{C_bP}$ và $\frac{A_4B}{A_4C}=\frac{A_cP}{A_cC}.\frac{A_bB}{A_bP}$ do đó 

Tương tự ta có $\frac{B_3C}{B_3A}=\frac{C_aP}{C_aA}.\frac{A_cC}{A_cP}$ và $\frac{B_4C}{B_4A}=\frac{B_aP}{B_aA}.\frac{B_cC}{B_cP}$ và $\frac{C_3A}{C_3B}=\frac{A_bP}{A_bB}.\frac{B_aA}{B_aP}$ và $\frac{C_4A}{C_4B}=\frac{C_bP}{C_bB}.\frac{C_aA}{C_aP}$. 

Từ đó $\frac{A_3B}{A_3C}.\frac{B_3C}{B_3A}.\frac{C_3A}{C_3B}=\frac{B_cP}{B_cC}.\frac{C_bB}{C_bP}.\frac{C_aP}{C_aA}.\frac{A_cC}{A_cP}.\frac{A_bP}{A_bB}.\frac{B_aA}{B_aP}$

Và $\frac{A_4B}{A_4C}.\frac{B_4C}{B_4A}.\frac{C_4A}{C_4B}=\frac{A_cP}{A_cC}.\frac{A_bB}{A_bP}.\frac{B_aP}{B_aA}.\frac{B_cC}{B_cP}.\frac{C_bP}{C_bB}.\frac{C_aA}{C_aP}$

Vậy  $\frac{A_3B}{A_3C}.\frac{B_3C}{B_3A}.\frac{C_3A}{C_3B}=1/(\frac{A_4B}{A_4C}.\frac{B_4C}{B_4A}.\frac{C_4A}{C_4B})$ nên $\frac{A_3B}{A_3C}.\frac{B_3C}{B_3A}.\frac{C_3A}{C_3B}=1\iff \frac{A_3B}{A_3C}.\frac{B_3C}{B_3A}.\frac{C_3A}{C_3B}=1$.

Ta hoàn thành chứng minh.

Theo cách chứng minh bài này thì chỉ cần $B_a,C_a$ bất kỳ trên đường thẳng $PA$ là được và tương tự các điểm còn lại !

Bài toán 150 (AoPS). Cho tam giác $ABC$ với $M$, $N$, $Q$ là trung điểm $AB$, $BC$ và $AC$. $P$ nằm trong tam giác và nằm trên phân giác $\angle BCA$. Gọi $D=AP\cap MN$ và $E=BP\cap MQ$. Chứng minh rằng $MD=ME$.

Cám ơn Bảo với lời giải rất nhanh, thầy đề nghị bài mới cho topic tiếp tục

Bài toán 139 (Nguyễn Lê Phước).  Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. $DE,DF$ cắt $AB,AC$ tại $M,N$. $IE,IF$ cắt $AB,AC$ tại $P,Q$. Chứng minh rằng trung điểm của $MN,PQ,BC$ thẳng hàng.

Do sơ suất mình đã đề nghị trùng bài toán 36, cám ơn Hoàng đã cho lời giải mới cho bài đó. Cám ơn Dương đã đóng góp lời giải, mình xin đề xuất lại đề toán 101.

Bài toán 101. Cho tam giác $ABC$ với đường cao $AH$. $M,N$ thuộc $BC$ sao cho $AM\perp AB, AN\perp AC$. $I$ là tâm nội tiếp tam giác $AMN$. $NI,MI$ cắt $CA,AB$ lần lượt tại $E,F$. Gọi $K,L$ là tâm nội tiếp tam giác $AHM,AHN$. Chứng minh rằng $EK,FL$ và $IH$ đồng quy.

Mình có post một tổng quát cho tính chất của bài toán 99. tại đây http://artofproblems...h498545p2801321 đã lâu, đó là một mở rộng sang conic, lời giải của Luis hay nhưng cũng phức tạp. Mở rộng này không gần gũi với toán Olympic lắm vậy hãy chỉ để tham khảo.

Lâu mình không tham giải, thực sự là phát hiện của Dương ở bài 54 khá thú vị. Nhân một bài Bảo vừa hỏi, mình thấy bài này có ý tưởng khá giống nên giải thử theo cách phương tích.

Sửa lại ký hiệu như sau cho tiện.

Cho tam giác $ABC$ trực tâm $H$. Dựng vào trong tam giác $PBC$ vuông cân tại $P$. Gọi $Q$ đẳng giác $P$ trong tam giác $ABC$. Chứng minh rằng $PQ$ đi qua $H$.

Lời giải. Do $Q$ đẳng giác $P$ nên gọi $E,F$ là hình chiếu của $Q$ lên $CA,AB$ dễ thấy tam giác $QFB$ và $QEC$ vuông cân. Vậy trong tam giác $QBC$ các tam giác $QFB$ và $QEC$ vuông cân dựng ra ngoài và tam giác $PBC$ vuông cân dựng vào trong nên $EPQF$ là hình bình hành từ đó dễ thấy $P$ là trực tâm tam giác $AEF$. Như vậy dễ thấy $P,H$ đều nằm trên trục đp của đường tròn đường kính $BE,CF$. Gọi $K,L$ là hình chiếu của $C,B$ lên $QF,QE$. Dễ thấy hai tam giác vuông $QCK$ và $QBL$ đồng dạng nên $QK/QL=QC/QB=QE/QF$ hay $QF.QK=QE.QL$. Từ đó $Q$ cũng thuộc trục đp của đường tròn đường kính $BE,CF$.

Bài toán này có phát biểu khá gần kiểu hình lớp 7, không rõ có cách nào THCS không ?

$\boxed{\text{Bài toán 55.}}$. Cho tam giác $ABC$ nhọn nội tiếp trong đường tròn $(O)$. Tiếp tuyến tại $A$ của $(O)$ cắt $BC$ tại $T$. $P$ nằm trong tam giác sao cho $TP=TA$. $PA,PB,PC$ lần lượt cắt $(O)$ tại $D,E,F$ khác $A,B,C$. Dựng tam giác cân $BAQ$ đồng dạng cùng hướng với $FOD$ và tam giác cân $CAR$ đồng dạng cùng hướng với $EOD$. Chứng minh rằng tâm ngoại tiếp tam giác $PQR$ nằm trên $AO$.

Cám ơn Dương đã gửi link, thầy có thể tổng kết lại được là bài tổng quát nên phát biểu như sau sẽ đẹp

Cho tam giác $ABC$ với trực tâm $H$ và tâm ngoại tiếp $O$. $P$ nằm trên trung trực $BC$ và $Q$ đẳng giác $P$. $PQ$ cắt $OH$ tại $R$. Chứng minh rằng $\frac{\overline{RH}}{\overline{RO}}=2-\frac{BC^2}{PC^2}$.

Lời giải trong link của Telv đã rõ ràng, tuy nhiên khi phát biểu như trên liệu có các đi khác ?

Trình bày lại latex cho Huy, lời giải trên đúng tuy nhiên phải dùng tới conic. Sau đây là lời giải dùng nghịch đảo

Giải. Chú ý rằng đường tròn $(M)$ qua $A,P$ và tiếp xúc $(PBC)$. Như vậy $(M)$ cắt $CA,AB$ tại $E',F'$ là đối xứng của $A$ qua $E,F$. Tương tự đường tròn $(N)$ qua $A,Q$ và tiếp xúc $(QBC)$ cắt $CA,AB$ tại $G',H'$ là đối xứng của $A$ qua $G,H$. Vậy ta cần chứng minh $E',F',G',H'$ cùng thuộc một đường tròn này tiếp xúc $BC$. Nghịch đảo cực $A$ phương tích bất kỳ. Chú ý rằng hai điểm đẳng giác vẫn có ảnh là hai điểm đẳng giác. Ta thu được bài toán sau của Bảo và Dương đã cm và phát biểu tại đây.

Cho tam giác $ABC$ có $P,Q$ là hai điểm đẳng giác. Tiếp tuyến tại $P$ của $(PBC)$ cắt $CA,AB$ tại $E,F$. Tiếp tuyến tại $Q$ của $(QBC)$ cắt $CA,AB$ tại $G,H$. Thì $E,F,G,H$ cùng thuộc một đường tròn tiếp xúc $(O)$.

Theo mình không nên phân biệt đối xử với tọa độ, đặc biệt là tọa độ Barycentric vì không phải vô cớ mà tờ báo hình sơ cấp lớn nhất thế giới  http://forumgeom.fau.edu/, đã nhiều năm qua dành thời lượng lớn để nghiên cứu về loại tọa độ này. Hơn nữa thực chất những việc biến đổi tỷ số trên đường thẳng, rồi những hệ thức của hàng điểm điểu hòa đều có gốc gác là đại số và tọa độ xạ ảnh. Mặt khác cũng không phải không có lý do mà Descartes được xếp vào một trong những nhà toán học vĩ đại nhất nhờ phương pháp của mình. Do đó nên dung hòa giữa đại số và hình.

Cám ơn Bảo đã post lại bài mở rộng bài toán miền Tây, sau đây là lời giải dùng hoàn toàn ý tưởng của Bảo được thầy làm chi tiết hơn.

$\boxed{\text{Lời giải bài toán 6.}}$ Ta dễ thấy các đường tròn $(GBE),(GCF)$ đi qua $K$ nên ta viết lại gọn hơn như sau

Đây là link gốc bài toán 60' 

http://www.artofprob...unity/c6h612592

$\boxed{\text{Bài toán 64.}}$ Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. $P$ bất kỳ nằm trong tam giác. $PB,PC$ lần lượt cắt $(O)$ tại $E,F$ khác $B,C$. $M,N$ lần lượt là đối xứng của $B,C$ qua $AF,AE$. $K$ là tâm ngoại tiếp tam giác $PMN$. Gọi $L$ đối xứng $K$ qua trung trực $AP$. Chứng minh rằng $PL\parallel AO$ khi và chỉ khi $\frac{PB}{PC}=\frac{AB}{AC}$.

Bài toán 88 đã có đáp án trên báo Epsilon 10, mình xin đề nghị một bài mới

$\boxed{\text{Bài toán 89.}}$ (Tập huấn đội dự tuyển KHTN 2016) Cho tam giác $ABC$ nhọn có đường cao $AA_0,BB_0,CC_0$, trung tuyến $AA_1,BB_1,CC_1$ tâm đường tròn Euler là $N$. Đường thẳng qua $A$ song song $BC$ cắt $B_0C_0$ tại $A_2$. $A_3$ là hình chiếu của $A_2$ lên $AA_1$. $A_4$ là trung điểm của $AA_2$. $A_5$ là đối xứng của $A_3$ qua $NA_4$. Tương tự có $B_5,C_5$. Chứng minh rằng $AA_5,BB_5,CC_5$ đồng quy.

Cám ơn Khánh, đúng là bài này ra như vậy bị dễ đi, ý tưởng là thầy muốn chứng minh $PL$ đi qua điểm Lemoine của $ABC$. Vậy ta tiếp tục

$\boxed{\text{Bài toán 86.}}$ Cho tứ giác $ABCD$ ngoại tiếp đường tròn $(I)$. Chứng minh rằng phân giác các góc $\angle AIC,\angle BID$ vuông góc.

Bổ đề. Cho tam giác $ABC$ cân tại $A$ có đường cao $CD$. Gọi $E$ là trung điểm của $BD$, $M$ là trung điểm $CE$, phân giác của $\angle{BDC}$ cắt $CE$ tại $P$. Đường tròn tâm $C$ bán kính $CD$ cắt $AC$ tại $Q$. Gọi $K$ là giao điểm của $PQ$ và $AM$.

$\boxed{\text{Bài toán 78.}}$ Cho tam giác $ABC$ có các tâm bàng tiếp góc $B,C$ là $K,L$. Lấy $P,Q$ trên $CK,BL$ sao cho $LP\parallel AC,KQ\parallel AB$. $PQ$ cắt $KL$ tại $R$. $H$ là hình chiếu của $R$ lên đường thẳng $OI$ của tam giác $ABC$. $AD$ là phân giác của tam giác $ABC$. $K$ thuộc $AD$ sao cho $KH\perp HA$. $HB,HC$ cắt $(HKD)$ tại $M,N$ khác $H$. $DN,DM$ cắt $CA,AB$ tại $E,F$. Chứng minh rằng bốn điểm $A,E,H,F$ thuộc một đường tròn.

Bài tập tập huấn đội IMO 2016.

Các giải khác cho bài 5 (dùng hình của Bảo) tránh dùng sin, chú ý hai tam giác $XBF$ và $XEC$ đồng dạng nên tỷ lệ diện tích là bình phương tỷ lệ đồng dạng.

Gọi $AX$ cắt $BC$ tại $U$ thì $\frac{UB}{UC}=\frac{[XAB]}{[XAC]}=\frac{[XAB]}{[XBF]}.\frac{[XBF]}{[XEC]}.\frac{[XEC]}{[XAC]}=\frac{AB}{BF}.\frac{BF^2}{CE^2}.\frac{CE}{AC}=\frac{AB.BF}{AC.CE}$. Tương tự dùng Ceva ta có điều phải chứng minh.

Chú ý hai tam giác $XBF$ và $XEC$ đồng dạng cùng hướng, ta có thể thay bằng diện tích đại số và độ dài đại số.