Mình làm thế này ko bít đúng ko :
Chọn $n= 1991.10^{x}.\frac{1}{d}$ vói $10^{x}>a$ là đuoc số cần tìm .

Sai do $n$ khi đó không nguyên!

Đề có cho n nguyên đâu e !

Ta có nhận xét là nếu $a \not\in\mathbb{Z}$ thì $[a]+[-a]= -1$
Xét : $[\frac{kq}{p}]+[\frac{(p-k)q}{q}]= [\frac{kq}{p}]+[q-\frac{kp}{q}]= q+[\frac{kq}{p}]+[-\frac{kq}{p}]$ $= q-1$
( vì do $(p,q)=1$ nên $\frac{kp}{q}\not\in\mathbb{Z}$ nên áp dụng NX trên thì ta có đc điều này )
Tương tự suy ra : $S= \frac{(p-1)(q-1)}{2}$
Dễ rồi !

Với mỗi số nguyên dương n, ký hiệu S(n) là tổng tất cả các chữ số trong biểu diễn thập phân của n.
Xét các số nguyên dương m là bội của 2003. Hãy tìm giá trị nhỏ nhất của S(m).

Đặt $p=2003\in\mathbb{P}$.
+ Nếu $S(n)= 1\Rightarrow n= 100...000= 10^{^{k}}\not\vdots 2003\Rightarrow S(n)> 1$
+ Nếu $S(n)= 2$$\Rightarrow n= 200...000$ hoặc $n=100...100...00= 10^{i}+10^{j}$
Ta có $n=200...000= 2.10^{k} \not\vdots 2003$ $\Rightarrow n=10^i+10^j$
$\Rightarrow 10^i+10^j\vdots 2003=p\Rightarrow 10^i= -10^j(Modp)$
$\Rightarrow 10^{i-j}= -1(Modp)$$\Rightarrow 10^k= -1(Modp)$ ( $k=i-j$ )
Dễ thấy $2^{10}= 1024\equiv 10^7(Modp)$ , suy ra :
$(2^{5k})^{2}= 2^{10k}\equiv (10^{k})^{7}\equiv -1(Modp)$
$\Rightarrow -1$ là số chính phương mod p suy ra $p$ có dạng $4k+1$
$\Rightarrow 2003=p= 4k+1\Rightarrow k= \frac{2002}{4} \not \in \mathbb{Z}$
Suy ra vô lí $\Rightarrow S(n)> 2$
+ Bây giờ ta chứng minh là có $n$ để $S(n)= 3$
Vì $p=2003\neq 8k-1\neq 8k+1$ suy ra $2$ không là SCP mod p $\Rightarrow 2^{\frac{p-1}{2}}\equiv -1(Modp))$
Mà $10^{7}\equiv 2^{10}(Modp)\Rightarrow 2.10^{700}\equiv 2^{1001}= 2^{\frac{p-1}{2}}\equiv -1 (Modp)$
$\Rightarrow (2.10^{700}+1)\vdots p$ .Mà $S(2.10^{700}+1)= 3$ nên khẳng định của ta là đúng.
Vậy $minS(n)= 3$.Xảy ra khi chẳng hạn $n= 2.10^{700}+1$

Với a,b,c là các số thực t/mđẳng thức a+b+c=0.CMR:
$2.(a^{5}+b^{5}+c^{5})=5abc(a^{2}+b^{2}+c^{2})$

Tù $a+b+c=0\Rightarrow a^{3}+b^{3}+c^{3}= 3abc$
$\Rightarrow (a^{2}+b^{2}+c^{2})(a^{3}+b^{3}+c^{3})= 3abc(a^{2}+b^{2}+c^{2})$
$\Leftrightarrow \sum a^{5}+\sum a^{3}(b^{2}+c^{2})= 3abc(a^{2}+b^{2}+c^{2})$ (1)
$a+b+c= 0\Leftrightarrow -a= b+c\Leftrightarrow a^{2}= b^{2}+c^{2}+2bc\Leftrightarrow b^{2}+c^{2}=a^{2}-2bc$
$(1)\Leftrightarrow \sum a^{5}+\sum a^{3}(a^{2}-2bc)= 3abc\sum x^{2}$
$(1)\Leftrightarrow \sum a^{5}+\sum a^{5}-2\sum a^{3}bc= 3abc\sum a^{2}$
$\Leftrightarrow 2\sum a^{5}= 3abc\sum a^{2}$ (đpcm )

Mỏ rộng : Giải PT : $ (x-n)^{p}-(x-n)^{q}= 0(p>q)$ ( p , q là số tụ nhiên ) .
Giải : $ PT\Leftrightarrow (x-n)^{q}[(x-n)^{p-q}-1]= 0$
Xảy ra các truong họp :
-$ (x-n)^{q}=0\Leftrightarrow x=n$
-$ (x-n)^{p-q}=1$
+ Nếu p-q lẻ thì$ x-n=1 \Leftrightarrow x=n+1$
+Nếu p-q chẵn thì có 2 TH :
1. $ x-n=1 \Leftrightarrow x=n+1$
2.$ x-n=-1 \Leftrightarrow x=n-1$
KL : -Nếu p-q lẻ thì PT có các nghiệm : x=n : x= n+1
-Nếu p-q chẵn thì PT có các nghiệm : x=n ; x=n-1 ; x=n+1 .

Đề bài : Giải phương trình : $(x-7)^1-(x-7)^{11}=0$
p/s : Đề đơn giản . Chỉ nghĩ được thế này thôi .

PT $\Leftrightarrow (x-7)[1-(x-7)^{10}]= 0$
Xảy ra các truòng hop :
-$ x-7= 0\Leftrightarrow x=7$
-$ x-7=1\Leftrightarrow x=8$
-$ x-7=-1\Leftrightarrow x=6$
Thủ lại : thỏa mãn .
Vậy nghiệm của Pt là : x=6 , x=7 , hoặc x=8 .

Lời giải chưa cụ thể.
D-B=5.4h
E=9.5
F=1 * 10=10
S=81.1

Đáp án:

Các số $ x^{4};y^{4};z^{4}$ chia 4 du 0 hoặc 1 mà $ (1984-104x)\vdots4$ suy ra $(x^{4}+y^{4}+z^{4})\vdots4$
Do đó $ x^{4};y^{4};z^{4}$ chia hết cho 4 suy ra x,y,z chẵn .
$ A= 20^{x}+11^{y}-1969^{z}= [20^{x}-(-1)^{x}]+[11^y-(-1)^{y}]$ $ -(1969^{z}-1^{z})$ +1 (*)
Vì $ (a^{n}-b^{n})\vdots(a-b)$ nên $ (20^{x}-(-1)^{x})\vdots21\vdots3$
$ (11^{y}-(-1)^{y})\vdots12\vdots3$ , $ (1969^{z}-1^{z})\vdots1968\vdots3$
suy ra A chia 3 du 1
Mà $ a+a^{2}= a(a+1)$ là tích 2 số nguyên liên tiếp nên chia 3 du 0 hoặc 2.
Vậy Số $ A= 20^{x}+11^{y}-1969^{z}$ ko thể viết duoi dạng $ a+a^{2}$ vs a là số tụ nhiên .

(*) $=20^{x}-1+11^{y}-1-(1969^{z}-1)+1= 20^{x}+11^{y}-1969^{z}$

Đáp án:

Các số $ x^{4};y^{4};z^{4}$ chia 4 du 0 hoặc 1 mà $ (1984-104x)\vdots4$ suy ra $(x^{4}+y^{4}+z^{4})\vdots4$
Do đó $ x^{4};y^{4};z^{4}$ chia hết cho 4 suy ra x,y,z chẵn .
$ A= 20^{x}+11^{y}-1969^{z}= [20^{x}-(-1)^{x}]+[11^y-(-1)^{y}]$ $ -(1969^{z}-1^{z})$ +1
Vì $ (a^{n}-b^{n})\vdots(a-b)$ nên $ (20^{x}-(-1)^{x})\vdots21\vdots3$
$ (11^{y}-(-1)^{y})\vdots12\vdots3$ , $ (1969^{z}-1^{z})\vdots1968\vdots3$
suy ra A chia 3 du 1
Mà $ a+a^{2}= a(a+1)$ là tích 2 số nguyên liên tiếp nên chia 3 du 0 hoặc 2.
Vậy Số $ A= 20^{x}+11^{y}-1969^{z}$ ko thể viết duoi dạng $ a+a^{2}$ vs a là số tụ nhiên .

Anh thấy đáp án có chỗ sai thì phải. Chỗ chứng minh A chia 3 dư 1.
Anh viết lại như sau cho dễ hiểu:
\[A = {20^x} + {11^y} - {1969^z} \equiv {\left( { - 1} \right)^x} + {\left( { - 1} \right)^y} - {\left( { - 1} \right)^z} \equiv 1 + 1 - 1 \equiv 1\left( {\bmod 3} \right)\]

Anh oi Đáp án đung rồi mà.x,y,z chẵn nên đúng mà anh .

Đề bài : Cho x ,y ,z nguyên duong thỏa mãn :
$ x^{4}+y^{4}+z^{4}= 1984-104x$
Hỏi : Số $ A= 20^{x}+11^{y}-1969^{z}$ có thể viết duoi dạng $ a+a^{2}$ vs a là số tụ nhiên đc không ?

Do sự cố kĩ thuật nên thời gian ra đề được tính là lúc 22h19 17/3/2012.

Đáp án:

Các số $ x^{4};y^{4};z^{4}$ chia 4 du 0 hoặc 1 mà $ (1984-104x)\vdots4$ suy ra $(x^{4}+y^{4}+z^{4})\vdots4$
Do đó $ x^{4};y^{4};z^{4}$ chia hết cho 4 suy ra x,y,z chẵn .
$ A= 20^{x}+11^{y}-1969^{z}= [20^{x}-(-1)^{x}]+[11^y-(-1)^{y}]$ $ -(1969^{z}-1^{z})$ +1
Vì $ (a^{n}-b^{n})\vdots(a-b)$ nên $ (20^{x}-(-1)^{x})\vdots21\vdots3$
$ (11^{y}-(-1)^{y})\vdots12\vdots3$ , $ (1969^{z}-1^{z})\vdots1968\vdots3$
suy ra A chia 3 du 1
Mà $ a+a^{2}= a(a+1)$ là tích 2 số nguyên liên tiếp nên chia 3 du 0 hoặc 2.
Vậy Số $ A= 20^{x}+11^{y}-1969^{z}$ ko thể viết duoi dạng $ a+a^{2}$ vs a là số tụ nhiên .

Gọi a, b, c là độ dài các cạnh BC, CA, AB của tam giác ABC (a, b, c >0)
Gọi x, y, z là độ dài các đoạn thẳng MH, MI, MK (x, y, z >0)
Vì MH, MI, MK vuông góc với BC, CA, AB nên ta có:2 S_BMC= $x.a$,2 S_CMA= $y.b$,2 S_AMB= $z.c$
Mà điểm M nằm trong tam giác ABC nên
2 S_ABC=2(S_AMB+S_BMC+S_CMA)=$ax+by+cz$
Áp dụng BĐT Cauchy-schwarz ta có:
4 $S_{ABC}^2$ = $(ax+by+cz)^2 \leq (a^2+b^2+c^2)(x^2+y^2+z^2)$
Do đó: $x^2+y^2+z^2 \geq \frac{4 S_{ABC}^2}{a^2+b^2+c^2}$
Hay $MH^2+MI^2+MK^2 \geq \frac{4 S_{ABC}^2}{a^2+b^2+c^2}$
mà a, b, c và $S_{ABC}^2$ không đổi
Suy ra $MH^2+MI^2+MK^2$ đạt GTNN là $\frac{4 S_{ABC}^2}{AB^2+BC^2+CA^2}$
khi và chỉ khi M nằm trong tam giác ABC thỏa mãn điều kiện:
$\frac{MH}{BC}=\frac{MI}{AC}=\frac{MK}{AB}$

Thiếu hình vẽ, trừ nửa số điểm. BĐT Bunyakovski cho 2 bộ 3 số ở THCS không được công nhận, trừ 4đ. Biện luận dấu = chưa hoàn chỉnh.
D-B=40.6h
E=0.5
F=0
S=8.9

Đặt $\ x^{2}= t$ phuong trình tuong đuong vói :
$ \sqrt[5]{27}t^{5}-5t^{3}+2\sqrt[5]{27}=0\Leftrightarrow 3t^{5}-5\sqrt[5]{3^{2}}t^{3}+6= 0$
$ \Leftrightarrow 3t^{3}(t^{2}-\sqrt[5]{3^{2}})-2\sqrt[5]{3^{2}}(t^{3}-\sqrt[5]{3^{3}})= 0$
$ \Leftrightarrow 3t^{3}(t-\sqrt[5]{3})(t+\sqrt[5]{3})-2\sqrt[5]{3^{2}}(t-\sqrt[5]{3})(t^{2}-\sqrt[5]{3}t+\sqrt[5]{3^{2}})= 0$
$ \Leftrightarrow (t-\sqrt[5]{3})(3t^{4}+3\sqrt[5]{3}t^{3}-2\sqrt[5]{3^{2}}t^{2}+2\sqrt[5]{3^{3}}t-2\sqrt[5]{3^{4}})= 0$
Mà $ 3t^{4}+3\sqrt[5]{3}t^{3}-2\sqrt[5]{3^{2}}t^{2}+2\sqrt[5]{3^{3}}t-2\sqrt[5]{3^{4}}\neq 0$ X
$ \Rightarrow t= \sqrt[5]{3}\Rightarrow x= \sqrt[10]{3}$ hoặc $ x= -\sqrt[10]{3}$
Vậy $\ x= \sqrt[10]{3}$ hoặc $ x= -\sqrt[10]{3}$

Chỗ dấu X nếu em lý luận chặt hơn thì sẽ được điểm tối đa.
Kết quả:
D-B=10.8h
E=8.5
F=0
S=62.7

Do MSS22 không post đề đúng thời hạn nên BTC đưa ra đề dự bị như sau:
Với $x,y,z$ là các tham số dương cho trước, giải hệ pt sau trên tập số dương:
\[
\left\{ \begin{array}{l}
ax + by + cz = xyz \\
\sqrt {a + b} + \sqrt {a + c} + \sqrt {b + c} =x+y+z \\
\end{array} \right.
\]

Lâu ko vào MSS chém tj'

Tù pt đầu $\Rightarrow \frac{a}{xy}+\frac{b}{yz}+\frac{c}{zx}= 1$
$\Rightarrow \frac{a}{yz}+\frac{b}{zx}< 1\Leftrightarrow ax+by< xyz\Rightarrow z> \frac{a}{y}+\frac{b}{x}$
Tuong tụ : $x> \frac{b}{z}+\frac{c}{y}$ , $y> \frac{a}{z}+\frac{c}{x}$
Áp dụng BĐT AM-GM ta đc :
$2(x+y+z)> \frac{b}{z}+\frac{c}{y}+ \frac{a}{z}+\frac{c}{x}+\frac{a}{y}+\frac{b}{x}+x+y+z$
$= (\frac{a+b}{z}+z)+(\frac{b+c}{x}+x)+(\frac{c+a}{y}+y)$
$\geq 2( \sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a})$
$\Rightarrow x+y+z> \sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}$
Vì dấu "=" ko xảy ra nên mâu thuẫn vs PT thú 2 của hệ .
Vậy hệ PT đã cho vô nghiệm .

Bài giải chính xác. Chuẩn ko cần chỉnh
D - B = 24h
E = 10
F = 0
S = 54

Em nộp bài :
Giả sủ phương trình có nghiệm và $x_0$ , $y_0$ , $z_0$ là nghiệm nhỏ nhất của phương trình .
Ta có : $ (36x+y)(36y+x)= 2^{z}$ (1)
Vì $ 2^{z}$ là lũy thùa của 2 nên cả hai thùa số $ (36x+y)$ và$ (36y+x)$ đều fải là lũy thùa của 2
hay $ (36x+y)\equiv 0(mod 2)$ và $ (36y+x)\equiv 0(mod 2)$ hay x,y chia hết cho 2 .
Giả sủ phương trình có nghiệm và $x_0,y_0,z_0$ là nghiệm nhỏ nhất của phương trình .
Đặt $x_0=2x_1 , y_0=2y_1$ ( $x_1 ,y_1$ là số tụ nhiên )
$(1)\Leftrightarrow (72 x_1 +2 y_1)+(72 y_1+2 x_1)= 2^{ z_0 }$
$\Leftrightarrow (36 x_1 + y_1 )(36 y_1+ x_1)= 2^{ z_0 -2}$
Đặt $z_0-2=z_1\Rightarrow x_1 , y_1 , z_1$ cũng là nghiệm của PT , nhung điều này vô lí vì
$x_1<x_0 , y_1<y_0, z_1<z_0$.
Vậy PT đã cho vô nghiệm .
________________________________________________________________________________________
Bài tổng quát :Giải PT nghiệm nguyên duong .
$(kx + y)(ky + x) = p^z$
vs p là số nguyên tố , k là số tụ nhiên chia hết cho p nhg ko fải là lũy thùa của p.
CM hoàn toàn tuong tu nhu trên .

Kết quả:
D-B=30.5
E=10
F=1 * 10=10
S=57.5

n chẵn nên lấy được 2 đỉnh làm đường kính đa giác, mỗi lần lấy tiền ở 2 đỉnh đối xứng nhau qua đường kính đó.Suy ra có thể .

Sr,nhầm vs n lẻ,bài này bất biến bt thôi

n lẻ phải chỉ ra cách làm chứ.

n chẵn. Mỗi đồng tiền ở đính $i$ gán cho số $i$ , nếu chuyển đến điỉnh nào ta lại đổi cho đồng đó số ấy.

Nếu làm được như vầy ta phải có $\frac{n(n+1)}{2}\equiv na(modn)$ vô lí với n chẵn.

Bài 5.2:
Gọi X là tập hợp các điểm đã cho trước.
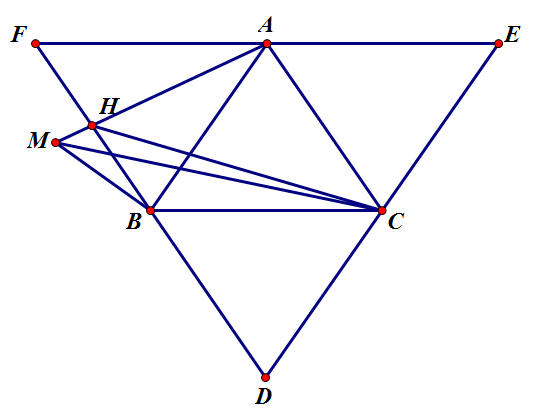
Trong các tam giác có 3 đỉnh thuộc tập X, ta chọn $\vartriangle ABC$ là tam giác có diện tích lớn nhất.
Các đường thẳng qua A,B,C thứ tự song song với BC,CA,AB đôi một cắt nhau tại D,E,F như hình vẽ.
Ta chứng minh mọi điểm của tập X đều nằm trong $\vartriangle DFE$, kể cả trên cạnh.
Giả sử, có 1 điểm M thuộc tập X sao cho M nằm ngoài $\vartriangle DFE$. Không mất tính tổng quát, giả sử vị trí của M nằm như hình vẽ.

Vẽ MA cắt FD tại H.
$S_{MAC}>S_{CAH}=S_{CAB}$: trái với cách chọn $\vartriangle ABC$ ban đầu.
Vậy ta có mọi phần tử của X đều nằm trong $\vartriangle DFE$ nên chúng nằm trong 1 trong 4 tam giác: ABC,ABF,ACE,BCD.
Theo nguyên lý Dirichlet, tồn tại 1 tam giác chứa 2012 điểm.
Lại có $S_{ABC}=S_{ABF}=S_{ACE}=S_{BCD}<1$ nên ta có đpcm.

Bài 6:
Cho tam giác $ABC$ có $AA';BB';CC'$ đồng quy tại $O$.Từ $A'$ kẻ $A'M$ vuông góc với $B'C'$.Từ $M$ hạ các đường vuông góc $MX,MY,MZ,MT$ xuống $OB';OC',AB';AC'$.Chứng minh rằng $X,Y,Z,T$ cùng thuộc một đường tròn

+ TH1 : $B^{'}C^{'}//BC$ dễ thấy $Q.E.D$
+ TH2 : $B^{'}C^{'}$ không song song với $BC$ . Gọi $K=B^{'}C^{'}\cap BC;S= B^{'}C^{'}\cap AA^{'}$
Suy ra $(KA^{'}BC)= -1\Rightarrow (SA^{'}OA)= -1$ ( qua phép chiếu xuyên tâm $B$
$\Rightarrow (AOSA^{'})= -1\Rightarrow M(AOSA^{'})= -1$
Mà lại có : $SM\perp A^{'}M\Rightarrow \angle SMA= \angle SMO\Rightarrow \angle C^{'}MA= \angle C^{'}MO$
Từ đây chỉ cần cộng góc thuần túy là ta có ngay $Q.E.D$

Nung nóng lại topic này nào.
-----------------
EXERCISE:
Cho a,b,c là các số thực dương. Chứng minh rằng:
$\left( {ab + bc + ca} \right)\left[ {{1 \over {{{\left( {a + b} \right)}^2}}} + {1 \over {{{\left( {b + c} \right)}^2}}} + {1 \over {{{\left( {c + a} \right)}^2}}}} \right] \ge {9 \over 4}$
--------------------

Cai' này là Iran 96 đúng ko nhi?

$4(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b})\geq 4.\frac{3}{2}=6$(Bất đẳng thức Netbitt)
Không mất tính tổng quát,giả sử:$b\geq a\geq c$
Ta xét hiệu:$ab^{2}+bc^{2}+ca^{2}+abc-(a^{2}b+b^{2}c+c^{2}a+abc)$
$a(b^{2}-c^{2})-a^{2}(b-c)-bc(b-c)=(b-c)(a-b)(c-a)\geq 0$
$\Rightarrow a^{2}b+b^{2}c+c^{2}a+abc\geq a^{2}b+b^{2}c+c^{2}a+abc \Leftrightarrow \frac{a^{2}b+b^{2}c+c^{2}a+abc}{a^{2}b+b^{2}c+c^{2}a+abc}\geq 1$
Vậy $VT\geq 6+1=7$ $\Rightarrow$ đpcm

saj rùi cậu oi ! k gỉ sủ đuọc $b\geq a\geq c$ o đây

Lâu lắm rồi mới được vào đây

Bài toán 399.[ Vasc ]
Cho các số thực dương $a, b, c$. Chứng minh rằng :
$$1+\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\ge 2\sqrt{1+\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}}$$

Bình phuong 2 vế và rút gọn ta đc ;
BĐT $\Leftrightarrow \sum \frac{a^{2}}{b^{2}}+2\sum \frac{a}{b}\geq 3+\sum \frac{b}{a}$
Đặt $\frac{a}{b}= x ,\frac{b}{c}= y,\frac{c}{a}= z\Rightarrow xyz=1$
BĐT trỏ thành :
$x^{2}+y^{2}+z^{2}+2(x+y+z)\geq 3+2(xy+yz+zx)$
Áp dụng BĐT : $x^{2}+y^{2}+z^{2}+2xyz+1\geq 2(xy+yz+zx)$
Ta đc:$\sum x^{2}+2\sum x\geq \sum x^{2}+6= (\sum x^{2}+2xyz+1)+3\geq 3+2\sum xy$
Đ.P.C.M
Xong!

Bài 426 . Cho các số thực không âm $a,b,c$ . Chứng minh rằng $\frac{a^{3}+b^{3}+c^{3}}{3}\geq abc+\frac{3}{4}\begin{vmatrix} (a-b)(b-c)(c-a) \end{vmatrix}$

BĐT $\frac{x^{3}+y^{3}+z^{3}-3xyz}{3}\geq \frac{3}{4}.\begin{vmatrix} (a-b)(b-c)(c-a) \end{vmatrix}$
$\Leftrightarrow \frac{(a+b+c).\sum (a-b)^{2}}{6}\geq \frac{3}{4}.\begin{vmatrix} (a-b)(b-c)(c-a) \end{vmatrix}$
Ta có :
$2(a+b+c)= \begin{vmatrix} a+b \end{vmatrix}+\begin{vmatrix} b+c\end{vmatrix}+\begin{vmatrix} c+a\end{vmatrix}\geq \begin{vmatrix} a-b \end{vmatrix}+\begin{vmatrix} b-c \end{vmatrix}+\begin{vmatrix} c-a\end{vmatrix}$
$\geq 3\sqrt[3]{\begin{vmatrix} a-b \end{vmatrix}\begin{vmatrix} b-c\end{vmatrix}\begin{vmatrix} c-a \end{vmatrix}}$
$\sum (a-b)^{2}\geq 3\sqrt[3]{(\begin{vmatrix} a-b \end{vmatrix}\begin{vmatrix} b-c \end{vmatrix}\begin{vmatrix} c-a \end{vmatrix})^{2}}$
$\Rightarrow VT= \frac{2(a+b+c)\sum (a-b)^{2}}{12}\geq \frac{9}{12}.\begin{vmatrix} a-b \end{vmatrix}\begin{vmatrix} b-c \end{vmatrix}\begin{vmatrix} c-a \end{vmatrix}= \frac{3}{4}.\begin{vmatrix} a-b \end{vmatrix}\begin{vmatrix} b-c \end{vmatrix}\begin{vmatrix} c-a \end{vmatrix}= VP$

Lâu lắm rồi mới được vào đây
Bài toán 394. [MOSP 2001]
Cho các số thực dương $a, b, c$ thoả $abc=1$. Chứng minh rằng :
$$(a+b)(b+c)(c+a)\ge 4(a+b+c-1)$$

Áp dụng BĐT quen thuộc : $\prod (a+b)\geq \frac{8}{9}\sum a.\sum ab$. Ta có :
BĐT $\Leftrightarrow \frac{8}{9}.\sum a.\sum ab\geq 4(\sum a-1)$
$\Leftrightarrow \frac{8}{9}.\sum ab+\frac{4}{\sum a}\geq 4$
Cái này đúng theo AM-GM:
$VT= \frac{4}{9}.\sum ab+\frac{4}{9}.\sum ab+\frac{4}{\sum a}\geq 3\sqrt[3]{\frac{4}{9}.\frac{4}{9}.\frac{(\sum ab)^{2}}{\sum a}}\geq 3\sqrt[3]{\frac{4}{9}.\frac{4}{9}.3}=4$
Xong .!

Bài 268: Cho a,b,c là các số thực dương thay đổi thỏa mãn a+b+c=3. CMR:
$\frac{a^2}{a+2b^3}+\frac{b^2}{b+2c^3}+\frac{c^2}{c+2a^3}\geq 1$

Ta có : $ \frac{a^{2}}{a+2b^{3}}= a-\frac{2ab^{3}}{a+2b^{3}}= a-\frac{2ab^{3}}{a+b^{3}+b^{3}}\geq a-\frac{2ab^{3}}{3b^{2}\sqrt[3]{a}}$
$$ \Rightarrow \frac{a^{2}}{a+2b^{3}}\geq a-\frac{2}{3}.\sqrt[3]{a^{2}}b = a-\frac{2}{3}.\sqrt[3]{ab.ab.b}\geq a-\frac{2}{9}(2ab+b)$$
Tương tự có 2 bđt nữa rồi cộng chúng lại , ta có :
$ VT\geq (a+b+c)-\frac{2}{9}.(2ab+2bc+2ca+3)\geq 1$
$\Rightarrow$ Đ.P.C.M .