Một giả thuyết giống định lý Cayley–Bacharach

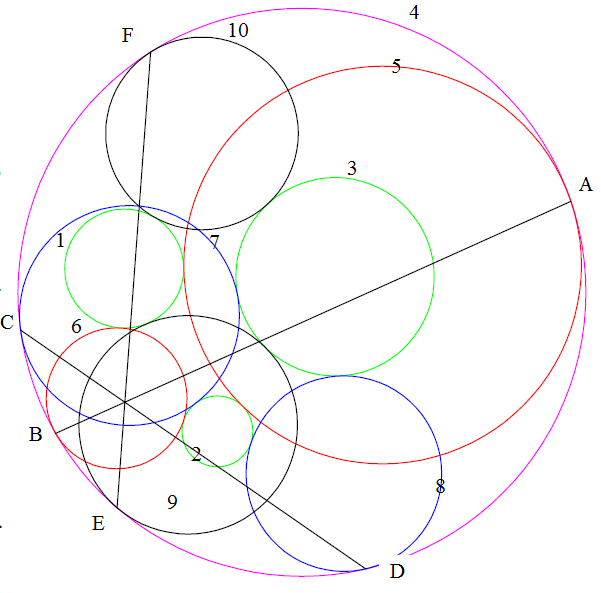
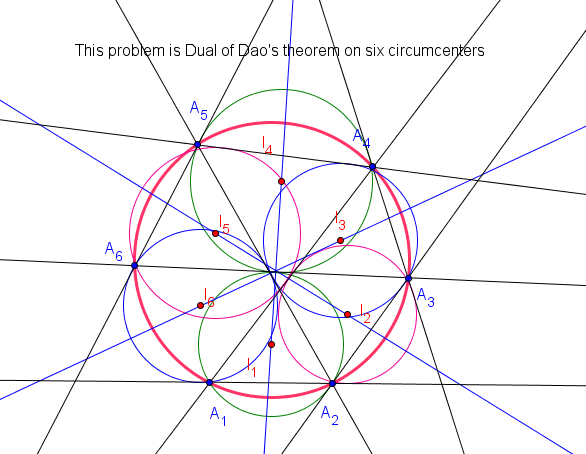
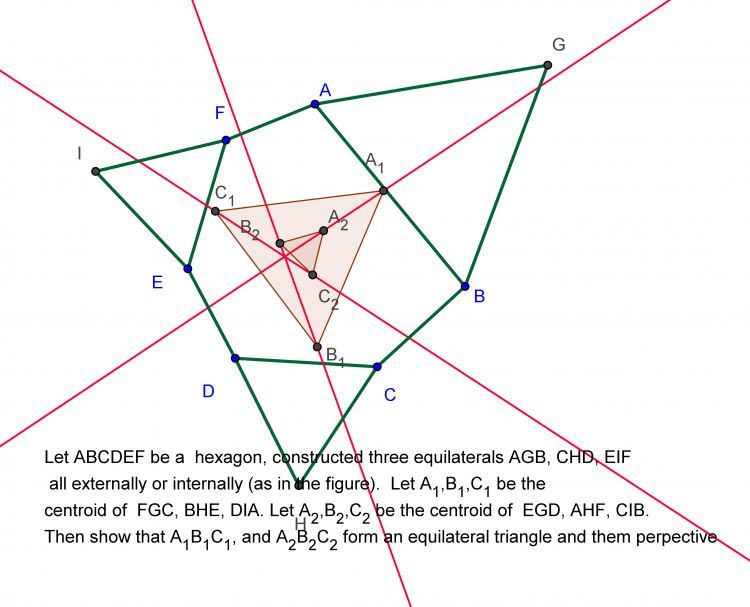
Giả thuyết 1: Cho sáu điểm $A, A', B, B', C, C'$ cùng nằm trên một đường bậc hai và đường bậc ba (nào đó). Cho một đường bậc hai đi qua $B, B', C, C'$ và cắt đường bậc ba đó tại $A_1, A_2$. Đường bậc hai đi qua $C, C', A, A'$ và cắt đường bậc ba đó tại $B_1, B_2$. Đường bậc ba đi qua $A, A', B, B'$ và cắt đường bậc ba tại $C_1, C_2$. Khi đó sáu điểm $A_1,A_2, B_1, B_2, C_1, C_2$ nằm trên một đường bậc hai. Nếu ta chọn trước các điểm $A_1, B_1, C_1$ thẳng hàng thì các điểm $A_2, B_2, C_2$ cũng phải thẳng hàng.

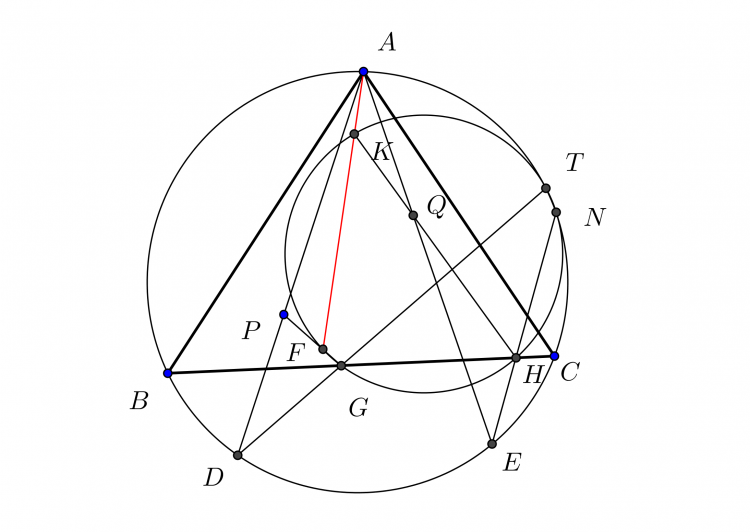
Giả thuyết 2: Cho một đường conic cắt một đường bậc ba tại 6 điểm $A, B, C, D, E, F$. Cho một đường conic khác đi qua ba điểm $A,B,C$ cắt đường bậc ba tại $G, H, I$, cho đường conic khác đi qua ba điểm $D, E, F$ cắt đường bậc ba tại $J, Q, K$. Khi đó sáu điểm $G, H, I, J, Q, K$ sẽ nằm trên một đường conic.

Chứng minh giả thuyết 2:
Đây là cách chứng minh cho giả thuyết 2 của một giáo sư (mà mình không hiểu) nhưng cứ trình bày lại ra đây để mọi người tham khảo: 

Áp dụng luật nhóm, nếu như một đường bậc hai giao với một đường bậc ba tại sáu điểm thì tổng sáu điểm phải bằng không. Ta có A+B+C+D+E+F=0; A+B+C+G+H+I=0; D+E+F+J+Q+K=0 => G+H+I+J+Q+K=0 => Sáu điểm G, H, I, J, Q, K nằm trên một đường conic. Giả thuyết mạnh hơn được chứng minh.

Giả thuyết tổng quát: Cho hai đường cong (đa thức) cắt nhau tại $\frac{d^2+3d}{2}+\frac{l^2+3l}{2}+2$ điểm. Nếu $\frac{d^2+3d}{2}+1$ điểm nằm trên đường cong bậc $d$ thì $\frac{l^2+3l}{2}+1$ điểm còn lại sẽ nằm trên đường cong bậc $l$

Vấn đề 10 đường tròn:

 Ten circles problem.pdf   29.82K   375 Số lần tải

 Another+then+circles+problem.pdf   54.19K   210 Số lần tải
 

Giả thuyết: Cho sáu điểm $A, A', B, B', C, C'$ nằm trên một đường conic. Đường conic qua bốn điểm $B, B', C, C'$ cắt đường thẳng $AA'$ at $A_1, A_2$. Đường conic qua bốn điểm $C, C', A, A'$ cắt đường thẳng $CC'$  tại $B_1, B_2$. Đường conic qua bốn điểm $A, A', B, B'$ cắt đường thẳng $CC'$ tại $C_1, C_2$. Khi đó sáu điểm $A_1,A_2, B_1, B_2, C_1, C_2$ nằm trên một đường conic. Do đó nếu chọn trước $A_1, B_1, C_1$ thẳng hàng thì các điểm $A_2, B_2, C_2$ cũng thẳng hàng.

Mở rộng định lý Pascal và định lý Brianchon

Cho sáu đường tròn $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$. Các đường tròn $(O_i)$, $(O_{i+1})$ cắt nhau tại các  điểm tại hai điểm $A_i$, $A'_i$ với $i=1, 2, 3, 4, 5, 6$ (Ở đây chúng ta lấy module 6). Chứng minh rằng nếu sáu điểm $A_1$, $A_2$, $A_3$, $A_4$, $A_5$, $A_6$ nằm trên một đường tròn và $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$  nằm trên một đường tròn khác.

1. Khi đó giao điểm của các cặp đường tròn $(O_1)$ và $(O_4)$,  $(O_2)$ và $(O_5)$, $(O_3)$ và $(O_6)$ (nếu tồn tại) sẽ nằm trên một đường tròn.

2. Các đường thẳng $O_1O_4, O_2O_5, O_3O_6$ sẽ đồng quy (Vấn đề này đã được công bố tại Problem 3845, Volum 39, trên tạp chí Crux Mathemticorum)

http://tube.geogebra.org/m/1539785

TẠI SAO TÔI PHÁT HIỆN RA KẾT QUẢ NÀY?

Định lý Pascal là một định lý nổi tiếng đặt theo tên nhà bác học Blaise Pascal (1623-1662). Nội dung như sau:

Cho một lục giác nội tiếp khi đó giao điểm của các cặp cạnh đối diện nằm trên một đường thẳng.

Ngày 29/08/2015 anh Nguyễn Ngọc Giang có đăng trên facebook một kết quả là mở rộng của định lý Pascal như sau:



Tôi nhìn vào cách mở rộng của anh Giang tôi thấy rằng sẽ có một lục giác đối xứng với đường tròn ngoại tiếp lục giác $ABCDEF$ ban đầu ở bên kia trục của đường thẳng d. Với kinh nghiệm "CHƠI" hình học phẳng mấy năm nay tôi hiểu rằng kết quả này có thể mở rộng thành một định lý tổng quát hơn bằng cách ta thay lục giác đối xứng đó trong kết quả của anh Giang bằng một lục giác nội tiếp bất kỳ, ở vị trí bất kỳ trong mặt phẳng. Tôi nghĩ như vậy và tôi kiểm tra qua phần mềm thấy ý tưởng của tôi hoàn toàn đúng đắn. Quan sát kỹ hơn tôi thấy rằng cấu trúc hình học này thực ra tôi đã tìm ra và đăng trên tạp chí Crux vào tháng 5/2014(mà tôi vẫn gọi là vấn đề (hoặc định lý) tám đường tròn. Vốn được tôi biết đến như là một mở rộng của định lý Brianchon (một định lý kép của định lý Pascal).

Nội dung mở rộng định lý Pascal và định lý Brianchon như sau:

Cho sáu đường tròn $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$. Các đường tròn $(O_i)$, $(O_{i+1})$ cắt nhau tại các  điểm tại hai điểm $A_i$, $A'_i$ với $i=1, 2, 3, 4, 5, 6$ (Ở đây chúng ta lấy module 6). Chứng minh rằng nếu sáu điểm $A_1$, $A_2$, $A_3$, $A_4$, $A_5$, $A_6$ nằm trên một đường tròn và $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$  nằm trên một đường tròn khác.

1. Mở rộng định lý Pascal: Khi đó giao điểm của các cặp đường tròn $(O_1)$ và $(O_4)$,  $(O_2)$ và $(O_5)$, $(O_3)$ và $(O_6)$ (nếu tồn tại) sẽ nằm trên một đường tròn (1)

Khi nào đường tròn này suy biến thành đường thẳng Pascal? Ở đây tôi chỉ ra hai cách để đường tròn này suy biến thành đường thẳng Pascal như sau:

Cách 1: Xây dựng như cách của anh Giang.

Cách 2: Nếu cho đường tròn qua $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$ suy biến thành một điểm đặt tên là điêm $M$, khi đó rõ ràng $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$ đều đi qua $M$. Giả sử các giao điểm còn lại của của $(O_1)$ và $(O_4)$,  $(O_2)$ và $(O_5)$, $(O_3)$ và $(O_6)$ là $A, B, C$ như vậy theo kết quả (1) $A, B, C, M$ nằm trên một đường tròn. Bây giờ nếu ta cho điểm M cứ tiến tới vô cùng khi đó đường tròn này sẽ biến thành một đường thẳng và $A, B, C$ chính là giao điểm của ba cặp cạnh đối diện của lục giác $A_1A_2A_3A_4A_5A_6$.

2. Mở rộng định lý Brianchon: Các đường thẳng $O_1O_4, O_2O_5, O_3O_6$ sẽ đồng quy (Vấn đề này đã được công bố tại Problem 3845, Volum 39, trên tạp chí Crux Mathemticorum)

Khi nào kết quả trên thu về định lý Brianchon? Ở đây tôi chỉ ra hai cách để kết quả trên suy biến thành định lý Brianchon.

Cách 1: Dựng hình sao cho các điểm Ai trùng với Ai' khi đó sẽ có phát biểu là:

Cho sáu đường tròn  $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$, giả sử các đường tròn $(O_i)$ tiếp xúc $(O_{i+1})$ (chúng ta lấy Modulo 6) và sáu điểm tiếp xúc này nằm trên một đường tròn khi đó đường thẳng  $O_1O_4, O_2O_5, O_3O_6$ đồng quy. Thực sự dễ dàng thấy rằng định lý Brianchon là trường hợp đặc biệt của kết quả này.

Cách 2: Cho $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$ suy biến thành một điểm (trùng nhau) đặt tên là điểm $M$ cho điểm này trùng với tâm đường tròn ngoại tiếp $A_1A_2A_3A_4A_5A_6$  sau đó vị tự tỉ số 2 ta sẽ có ngay định lý Brianchon.

Cho một đường conic $S$ và điểm $P$ trên mặt phẳng, ba đường thẳng qua P cắt conic lần lượt cắt đường conic tại các điểm $A, A'; B, B'; C, C'$. Nếu $D$ nằm trên đường thẳng cực của $P$ hoặc $D$ nằm trên đường conic thì $A'D, B'D, C'D$ lần lượt cắt ba cạnh $BC, CA, AB$ tại ba điểm $A_0, B_0, C_0$ thẳng hàng. Hơn thế bốn điểm $A_0, B_0, C_0, P$ thẳng hàng khi và chỉ khi $D$ nằm trên đường conic.

Kết quả trên là mở rộng của các định lý sau:

1. Định lý Droz-Farny,

2. định lý Goormaghtigh,

3. định lý đường thẳng Đào (hẹp),

4. định lý Zaslavsky,

5. định lý Colling,

6. định lý Simsson,

7. Vấn đề Adam Bliss

Kết quả trên được chứng minh trong các bài báo của:

* Nguyen Ngoc Giang, A proof of Dao theorem, Global Journal of Advanced Research on Classical and Modern Geometries, ISSN: 2284-5569, Vol.4, (2015), Issue 2, page 102-106
* Son Tran Hoang (2014), A synthetic proof of Dao's generalization of Goormaghtigh's theorem. Global Journal of Advanced Research on Classical and Modern Geometries, volume 3, pages 125–129, ISSN 2284-5569

* O.T.Dao 2013, Two Pascals merge into one, Cut-The-Knot

* Geoff Smith (2015). 99.20 A projective Simson line. The Mathematical Gazette, 99, pp 339-341. doi:10.1017/mag.2015.47
 

Định nghĩa đường tròn $O_a$ là đường tròn tiếp xúc với đường tròn bàng tiếp $(E_b), (E_c)$ và đường tròn ngoại tiếp lần lượt tại $A_b, A_c$ và $A$. Xác định $B_c, B_a, C_a, C_b$ tương tự. Khi đó tam giác tạo bởi ba đường thẳng $A_bA_c, B_cB_a, C_aC_b$ là một tam giác perpective với rất nhiều tam giác:

1-$A_1B_1C_1$ thấu xạ với tam giác ABC

2-$A_1B_1C_1$ thấu xạ với tam giác excentral

3-$A_1B_1C_1$ thấu xạ với tam giác Cevian của điểm Nagel

4-$A_1B_1C_1$ thấu xạ với tam giác cevian  của điêm tâm đường tròn nội tiếp

5-$A_1B_1C_1$ thấu xạ với tam giác Feuerbach

6-$A_1B_1C_1$ thấu xạ với tam giác Extangents

7-$A_1B_1C_1$ thấu xạ với tam giác Apollonius

Phần trên tôi xây dựng tam giác $ABC$ với đường tròn bàng tiếp, tại đây tôi dựng với đường tròn nội tiếp kết quả tương tự.

Dựng đường tròn $O_a$ tiếp xúc với đường tròn ngoại tiếp tại $A$ và đường tròn nội tiếp tại $A'$. Định nghĩa $B', C'$ tương tự. Tiếp tuyến của đường tròn nội tiếp tại ABC tạo ra tam giác $A_1B_1C_1$

1- $A_1B_1C_1$ thấu xạ với tam giác ABC
2- $A_1B_1C_1$ thấu xạ với tam giác excentral 
3- $A_1B_1C_1$ thấu xạ với tam giác Cevian của điểm Gergonne (điểm thấu xạ trùng với 2-)
4- $A_1B_1C_1$ thấu xạ với tam giác cevian của điêm tâm đường tròn nội tiếp
5- $A_1B_1C_1$ thấu xạ với tam giác Feuerbach 
6- $A_1B_1C_1$ thấu xạ với tam giác Extangent 
7- $A_1B_1C_1$ thấu xạ với tam giác Apollonius

chú làm thế nào để đưa được hình vẽ lên thế ạ

Cháu vào chỗ Sử dụng bộ soạn thảo đầy đủ, ở góc hộp soạn thảo phía bên dưới tay phải. Sẽ hiện ra choose file (nghĩa là chọn file). Sau khi cháu click vào đó sẽ có đường link đến hình ảnh, Tiếp theo cháu click vào chỗ đính kèm file này. Sau đó chọn thêm vào bài viết ở góc hộp soạn thảo phía bên dưới tay phải:

Một số vấn đề về đường tròn Apollonian

Mở rộng bổ đề Sawayama

Cho tam giác $ABC$, $P$, $Q$ là hai điểm đẳng giác của nhau. $AP$, $AQ$ cắt đường tròn ngoại tiếp lần lượt tại $D, E$. Hai đường thẳng bất kỳ qua $D, E$ cắt đường tròn ngoại tiếp lần lượt tại hai điểm $T, N$ và cắt đường thẳng BC tại hai điểm $G, H$. Gọi $PG, HQ$ cắt đường tròn $(GHNT)$ tại $K, F$. Khi đó $K, F, A$ thẳng hàng.

Thầy Nguyễn Văn Linh chứng minh định lý mở rộng đường thẳng Simson trong file đính kèm.

   Nguyen Van Linh proof Dao generalization of the Simson line.pdf   60.35K   290 Số lần tải
 

Chứng minh khác tại đây : http://www.cut-the-k...ionSimson.shtml

Một số tam giác đều dựng từ một tam giác cho trước

Vấn đề: Dual của định lý Đào về sáu tâm đường tròn ngoại tiếp (đây là đường tròn nội tiếp).

Cho một lục giác nội tiếp, khi đó đường thẳng nối tâm các đường tròn nội tiếp các tam giác tạo bởi hai cạnh và chung đường chéo chính sẽ đồng quy.

http://tube.geogebra.org/m/1488371

Dual của định lý Maxwell.

Cho tam giác $ABC$, và đường thẳng $L$. Đường thẳng $L$ cắt ba cạnh $BC, CA, AB$ tại $A_1, B_1, C_1$. Gọi $A'B'C'$ la tam giác trong mặt phẳng đó sao cho $B'C', C'A', A'B'$ là song song với $AA_1, BB_1, CC_1$. Chứng minh rằng ba đường thẳng đi qua  $A', B', C'$ và lần lượt song song với $BC,CA,AB$ sẽ cắt ba cạnh $B'C', C'A', A'B'$ tại ba điểm thẳng hàng.

Liên quan đến định lý lá cờ Anh viết cùng thầy Nguyễn Minh Hà

 La co nuoc Anh.pdf   356.99K   1280 Số lần tải

Dao Thanh Oai, Equilateral triangles and Kiepert perspectors in complex numbers, 105--114.

 FG201509.pdf   94.99K   464 Số lần tải

Dao Thanh Oai, A family of Napoleon triangles associated with the Kiepert configuration, The Mathematical Gazette, Published online: 13 March 2015

http://journals.camb...d=0&issueId=544

 TamgiaNapoleon.pdf   309.59K   479 Số lần tải

Chứng minh định lý Simson mở rộng của hai tác giả Nguyễn Lê Phước và Nguyễn Chương Chí

 Chung_minh_dinh_ly_mo_rong_duong_thang_Sim_Son.pdf   429.42K   719 Số lần tải

Mở rộng định lý Napoleon kết hợp với một lục giác:

Cho $ABCDEF$ là một lục giác bất kỳ, dựng ba tam giác đều $AGB$, $CHD$, $EIF$ cùng ra ngoài hoặc cùng vào trong(hình vẽ đính kèm là dựng ra ngoài). Ta gọi $A_1,B_1,C_1$ lần lượt là trọng tâm của các tam giác $FGC, BHE, DIA$ và $A_2,B_2,C_2$ lần lượt là trọng tâm của các tam giác $EGD, AHF, CIB$. Khi đó hai tam giác $A_1B_1C_1$ và $A_2B_2C_2$ là các tam giác đều và chúng thấu xạ.

Vấn đề của một lục giác lồi nội tiếp và sáu đường tròn Thebault.

Cho lục giác $ABCDEF$ lồi nội tiếp đường tròn $(O)$. Gọi $A_1,B_1,C_1,D_1,E_1,F_1$ lần lượt là các tiếp điểm chung của sáu đường tròn Thebault $(FA,BC,(O))$, $(AB,CD,(O))$, $(BC,DE,(O))$, $(CD,EF,(O))$, $(DE,FA,(O))$, $(EF,AB,(O))$ với $(O)$. Hãy chứng minh $A_1D_1, B_1E_1, C_1F_1$ đồng quy.

http://tube.geogebra.org/m/1352263

Mở rộng định lý Sondat:

Cho tam giác $ABC$, cho $P$ là một điểm bất kỳ trên mặt phẳng, cho đường thẳng $d$ cắt ba cạnh tam giác tại $A_0$, $B_0$, $C_0$ ba đường thẳng tương ứng qua $A_0,B_0,C_0$ và song song với $AP, BP, CP$ tạo thành tam giác $A_1,B_1,C_1$. Theo định lý Maxwell thì ba đường thẳng qua $A_1, B_1, C_1$ và song song với $BC,CA,AB$ một cách tương ứng lại sẽ đồng quy tại một điểm ta gọi điểm này là $P_1$. Khi đó đường thẳng $d$ chi đôi đoạn thẳng $PP_1$. Trong trường hợp $P$ là trực tâm vấn đề này là định lý Sondat.

http://tube.geogebra.org/m/1467027

https://groups.yahoo...s/messages/2673

Lời giải cho vấn đề tám đường tròn, Proposed by Đào Thanh Oai, solution by Luis Gonzalez

Cách xác định $A_1$ còn mờ ám. Vì có hai vị trí $A_1$ (vị trí còn lại nằm ở cung đối diện). Tương tự với $B_1,C_1,...$

Thực ra anh cũng nhận ra điều đó(nhưng lười viết), cảm ơn em nhé. Anh bổ sung như sau:

Nếu đường tròn $A_1$ như hình vẽ thì tất cả các đường tròn Thebault tương ứng với $B_1,C_1,...,F_1$ còn lại như hình vẽ.
Nếu đường tròn tương ứng với $A_1$ phía đối diện thì tất cả các đường trờn tương ứng với $B_1,C_1,...,F_1$ cũng nằm ở phía đối diện
Nếu đường tròn tương ứng với $A_1$ nằm ngoài thì tất cả các đường tròn tương ứng $B_1,C_1,...,F_1$ cũng năm phía ngoài.(nằm ngoài cũng có hai trường hợp)

 

Vấn đề mở rộng định lý Feuerbach–Luchterhand

Vấn đề được nêu trong file đính kèm

 June-14-2014-Feuerbach-Luchterhand.pdf   106.14K   547 Số lần tải

Định lý Gossard và một phiên bản mở rộng đẹp. 

http://tube.geogebra...student/m645553

 Xét tam giác $ABC$ , đường thẳng $L$ cắt đt Euler của $ABC$ ở $D$ và $L$ cắt $BC$ , $CA$ , $AB$ lần lượt ở $A_0 , B_0 , C_0$ . Gọi $(H_a,O_a) , (H_b,O_b) , (H_c,O_c)$ lần lượt là trực tâm, tâm ngt của $AB_0C_0,BC_0A_0,CA_0B_0$. Gọi $D_a , D_b , D_c$  nằm trên đt Euler  $AB_0C_0,BC_0A_0,CA_0B_0$ thỏa mãn: 

\[ \frac{\overline{D_aH_a}}{\overline{DaOa}}=\frac{\overline{D_bH_b}}{\overline{D_bO_b}}=\frac{\overline{D_cH_c}}{\overline{D_cO_c}} \space=\frac{\overline{DH}}{\overline{DO}}=t  \].

Tam giác $A_1B_1C_1$ tạo bởi 3 đường thẳng qua $D_a,D_b,D_c$ song song $BC , CA , AB$

Chứng minh:

1-$A_1B_1C_1$ vị tự và đối xứng với $ABC$ qua một điểm nằm trên đường thẳng $L$. Khi $t=\infty$  hoặc đường thẳng $L$ trùng với đường thẳng Euler vấn đề này suy biến thành định lý Zeeman-Gossard.

2-Đường thẳng Newton của bốn tứ giác tạo bởi các đường thẳng $(AB,BC,CA,L)$, $(AB,AC,B_1C_1,L)$, $(BC,BA,C_1A_1,L)$ và $(CA,CB,A_1B_1,L)$ cũng đi qua tâm vị tự của hai tam giác $ABC$ và $A_1B_1C_1$

(Phạm Khoa Bằng dịch từ Geogebratube)