Cám ơn Phương. Bài này mình cũng đã post trên AoPS ở đây và đáp án này cũng do mình đề nghị. Trước hết ta viết bài toán lại cho đường tròn nội tiếp cho dễ nhìn, hai cách viết chứng minh giống hết nhau

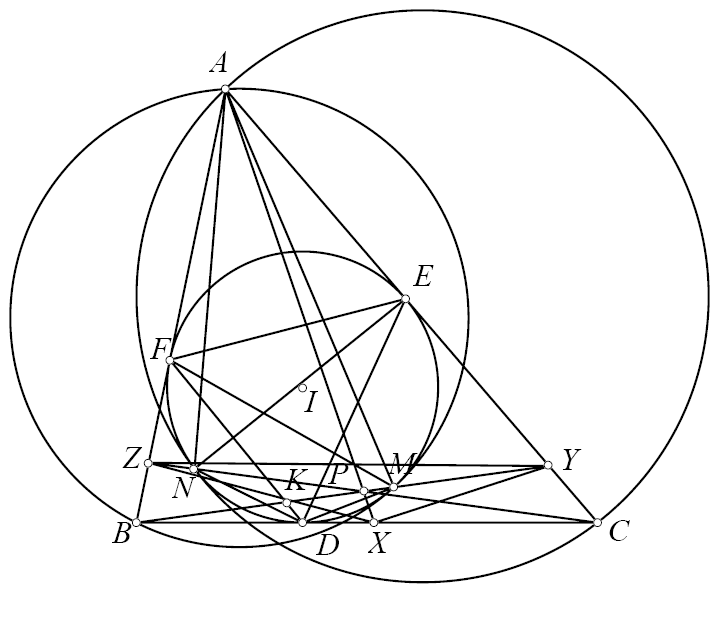
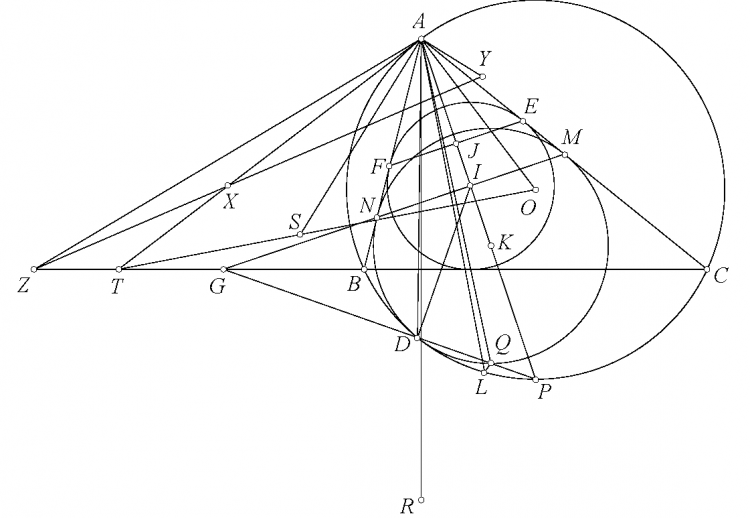
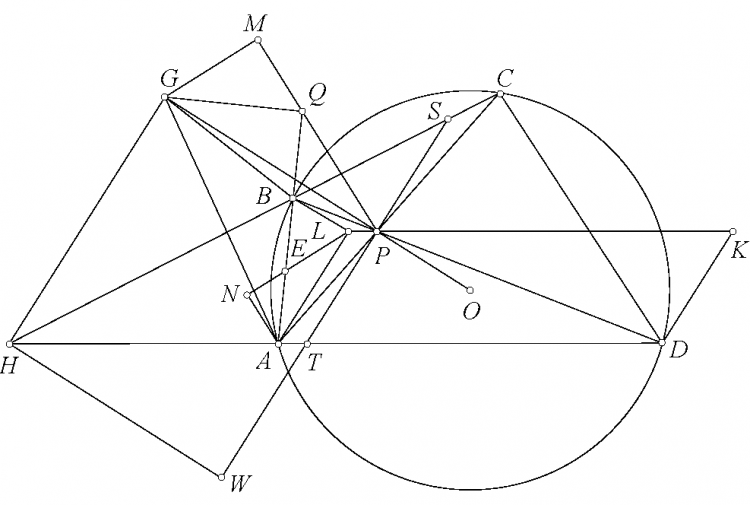
Bài toán 136'. Cho tam giác $ABC$ với đường tròn nội tiế $(I)$ tiếp xúc $BC$ tại $D$. Đường tròn qua $A,B$ tiếp xúc $(I)$ tại $M$. Đường tròn qua $A,C$ tiếp xúc $(I)$ tại $N$. $BM$ cắt $CN$ tại $P$. Chứng minh rằng $\angle PAB=\angle DAC$.

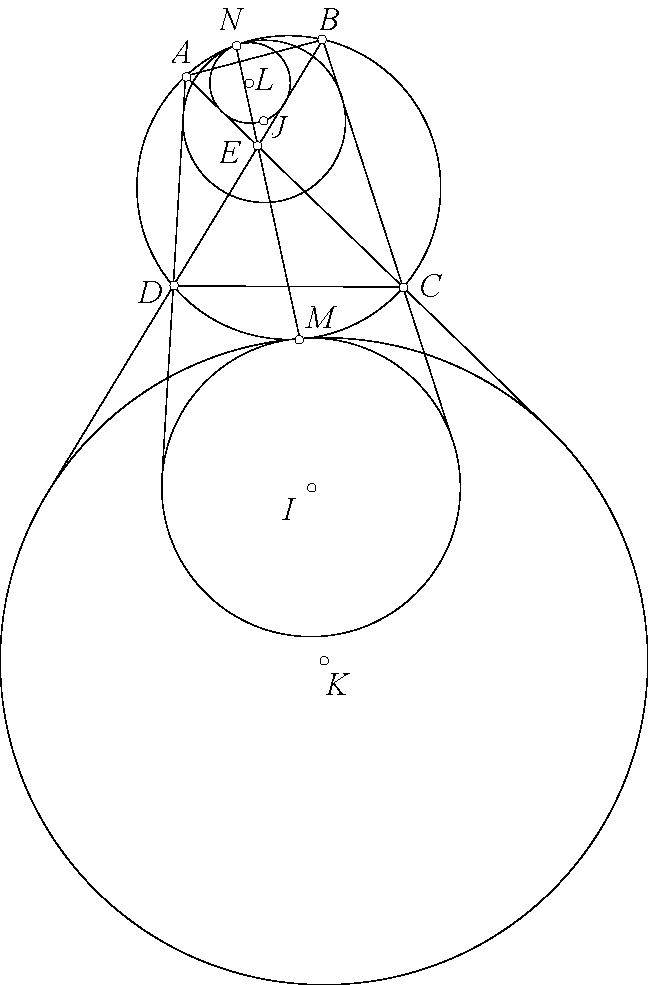
Bổ đề. Cho tam giác $ABC$ với đường tròn nội tiếp $(I,r)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. Đường tròn qua $B,C$ tiếp xúc $(I)$ tại $X$ thì

i) $\frac{XE.XF}{XD^2}=\frac{r^2}{IB.IC}.$

ii) $\frac{XE}{XF}=\frac{IB.DE^2}{IC.DF^2}.$

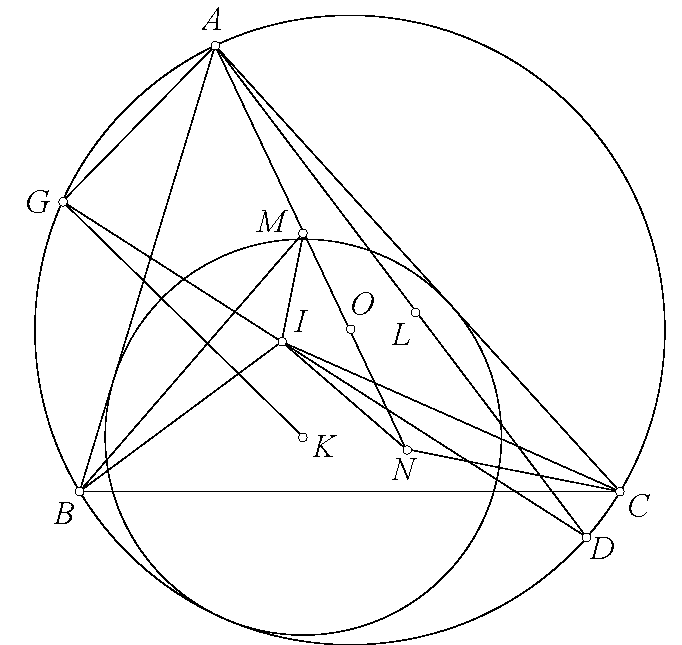
Chứng minh. Sử dụng chứng minh trong bài G7 SL 2002 quen thuộc, gọi $DK$ là đường kính của $(I)$ thì $XK,EF,BC$ đồng quy tại $G$. $AD$ cắt $EF$ tại $H$. Ta có $\frac{XE}{XF}.\frac{KE}{KF}=\frac{GE}{GF}=\frac{HE}{HF}=\frac{[AED]}{[AFD]}=\frac{DE}{DF}.\frac{DB}{IC}.\frac{IB}{DC}$ và chú ý $KE.IC=2r^2=KF.IB$. Vậy nên $\frac{XE}{XF}=\frac{IB.DE^2}{IC.DF^2}$ và $\frac{FX}{FK}.\frac{EX}{EK}=\frac{GX}{GK}=\frac{GD^2}{GK^2}=\frac{XD^2}{4r^2}$ và chú ý $KE.IC=2r^2=KF.IB$. Nên $\frac{XE.XF}{XD^2}=\frac{r^2}{IB.IC}.$

Hệ quả. $\dfrac{XE^2}{XD^2}=\dfrac{r^2.DE^2}{IB^2.DF^2}$ and $\dfrac{XF^2}{XD^2}=\dfrac{r^2.DF^2}{IC^2.DE^2}$.

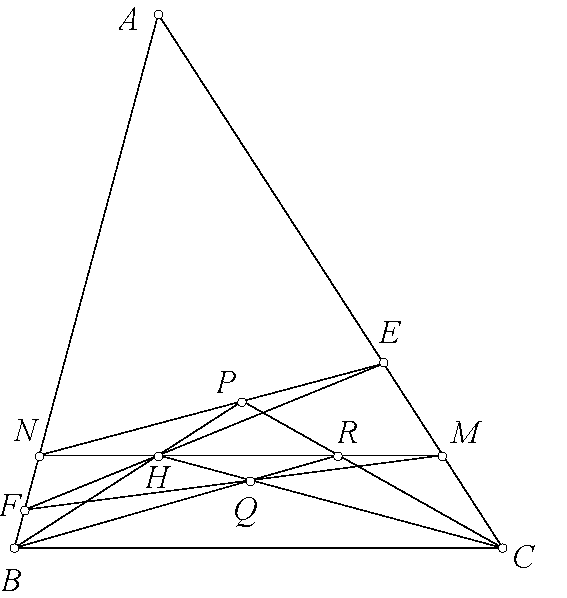
Giải bài toán. Gọi $(I)$ tiếp xúc $CA,AB$ tại $E,F$. $XYZ$ là tam giác Ceva của $P$. Gọi $BY$ cắt $DF$ tại $K$. Ta có $\frac{YC}{YA}=\frac{[YBC]}{[YBA]}=\frac{[YBC]}{[KBD]}.\frac{[KBD]}{[KBF]}.\frac{[KBF]}{[YBA]}=\frac{BC.BY}{BD.BK}.\frac{KD}{KF}.\frac{BF.BK}{BY.BA}=\frac{BC}{BA}\frac{MD^2}{MF^2}=\frac{BC}{BA}.\frac{r^2.DF^2}{EF^2.IA^2}.$ Tương tự, $\frac{ZB}{ZA}=\frac{BC}{CA}.\frac{r^2.DE^2}{EF^2.IA^2}$. Sử dụng định lý Ceva thì $\frac{XB}{XC}=\frac{YA}{YC}.\frac{ZB}{ZA}=\frac{AB.DE^2}{AC.DF^2}$. Vì vậy nên $\frac{DB}{DC}.\frac{XB}{XC}=\frac{p-b}{p-c}.\frac{AB.DE^2}{AC.DF^2}=\frac{DF.IB}{DE.IC}.\frac{AB.DE^2}{AC.DF^2}=\frac{AB^2}{AC^2}$. Do đó $AD,AX$ đẳng giác.

Bài này của Phương thực chất là một bổ đề khá quen thuộc sau

Bổ đề. Tứ giác $ABCD$ nội tiếp đường tròn $(O)$. Đường tròn $(I)$ tiếp xúc $AD,BC$ và tiếp xúc ngoài cung nhỏ $CD$ tại $M$. Đường tròn $(J)$ tiếp xúc $AD,BC$ và tiếp xúc trong cung nhỏ $AB$ tại $N$. Chứng minh rằng $MN,BD,AC$ đồng quy.

Chứng minh. Theo bổ đề Poncelet thì đường tròn $(K)$ tiếp xúc $DB,DC$ tiếp xúc ngoài cung nhỏ $CD$ thì tiếp điểm cũng là $M$. Tương tự đường tròn $(L)$ tiếp xúc $DB,DC$ tiếp xúc trong cung nhỏ $AB$ thì tiếp điểm cũng là $N$. Gọi $DB$ cắt $AC$ tại $E$ thì $E$ là tâm vị tự trong của $(K),(L)$ nên theo định lý Monge thì $M,N,E$ thẳng hàng hay $MN,BD,AC$ đồng quy.

Giải bài toán. Áp dụng bổ đề cho tứ giác $MEND$ nội tiếp. Ta thu được điều phải chứng minh.

Bài toán 138 (Mở rộng T12/471 THTT). Cho tam giác $ABC$ nội tiếp $(O)$ và tâm nội tiếp $I$. $D$ thuộc cung $BC$ không chứa $A$ của $(O)$. $DB,DC$ cắt $(IAB),(ICA)$ tại $P,Q$ khác $B,C$. $M,N$ thuộc $BC$ sao cho $MP,QN$ cùng vuông góc với $PQ$. Chứng minh rằng tâm đường tròn $(AMN)$ nằm trên $DO$.

Cảm ơn Quân và Khánh, bài toán 133 thầy chế lại từ đây http://artofproblems...nity/c6h1279917, mục đích của thầy là lấy điểm $R$ thuộc $MN$ sao cho $AR\perp EF$ rồi sau đó chứng minh $BQ,CP$ đi qua $R$ nhưng Quân chứng minh cách khác đẹp. Chú ý rằng bài toán này và bài toán của Khánh có thể đúng với $H$ bất kỳ thay vì trực tâm. Nhưng để chứng minh $AR\perp EF$ thì cần $H$ là trực tâm.

Bài toán 134. Cho tam giác $ABC$ và $DEF$ là tam giác pedal của $P$ bất kỳ. $(DEF)$ cắt $BC$ tại $G$ khác $D$. Đường thẳng qua $P$ vuông góc với $EF$ cắt $DE,DF$ tại $M,N$. Đường tròn $(DMN)$ cắt $(DEF)$ tại $Q$ khác $D$. Lấy $T$ sao cho $TM\perp AC,TN\perp AB$. $AT$ cắt $BC$ tại $S$. Chứng minh bốn điểm $A,Q,G,S$ đồng viên.

Cám ơn Khánh về lời giải rất ngắn gọn. Bài này thầy dạy đội tuyển KHTN đã lâu rồi nên chưa tìm lại được link gốc. Mình xin đề nghị bài tập tiếp cho topic tiếp tục

Bài toán 133 (Chế lại từ AoPS). Cho tam giác $ABC$ nhọn với trực tâm $H$. Một đường thẳng qua $H$ cắt cạnh $CA,AB$ tại $E,F$. Một đường thẳng qua $H$ song song $BC$ cắt $CA,AB$ tại $M,N$. $HB,HC$ lần lượt cắt $EN,FM$ tại $P,Q$. Chứng minh rằng $BQ,CP,MN$ đồng quy.

Cám ơn Việt và Quân, thầy đề nghị bài tiếp cho topic tiếp tục

Bài toán 132. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ với đường kính $AD,BE,CF$. $P$ là điểm bất kỳ. $PD,PE,PF$ cắt $(O)$ tại $X,Y,Z$ khác $D,E,F$. Gọi $U,V,W$ là tâm Euler của tam giác $XBC,YCA,ZAB$. Chứng minh rằng đường tròn ngoại tiếp tam giác $UVW$ đi qua tâm Euler của tam giác $ABC$.

Vừa rồi kết quả VMO khá khả quan với một số thành viên của diễn đàn, mình xin gửi lời chúc mừng tới các bạn. Để đầy mạnh phong trào đồng thời cũng có ý nghĩa cho việc chuẩn bị vòng 2, mình xin mạn phép đầy nhanh tốc độ Marathon bằng cách đề nghị song song thêm 2-3 bài toán, ai giải xong bài nào cứ tiếp tục đề nghị số thứ tự tiếp tục, làm thế để tăng số lượng bài và tăng hiệu suất làm việc, mong các bạn khi giải xong đề nghị các bài toán mới sát với vòng 2 để chúng ta cùng ôn tập luôn. Chúng ta vẫn duy trì quy tắc sau 2 ngày nếu chưa ai giải thì người đề nghị post đáp án !

Bài toán 143 (Tập huấn IMO 2013). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. $P$ là điểm bất kỳ. Đường thẳng qua $P$ vuông góc với $BC$ cắt $CA,AB$ tại $A_1,A_2$. Gọi $(K_a)$ là đường tròn ngoại tiếp tam giác $AA_1A_2$. Tương tự có $(K_b),(K_c)$. Gọi $(K)$ là đường tròn tiếp xúc trong với $(K_a),(K_b),(K_c)$. Gọi $(L)$ là đường tròn tiếp xúc ngoài với $(K_a),(K_b),(K_c)$. Chứng minh rằng các đường tròn $(O),(K),(L)$ đồng trục.

Cám ơn Dương lời giải của em cũng tương tự lời giải của Luis đưa ra ở đây nên thầy không dịch lại lời giải trong link nữa. Xin đề nghị bài tập tiếp

Bài toán 146. Cho tam giác $ABC$ với trực tâm $H$. $D$ là điểm nằm cũng phía $A$ với $BC$. $E,F$ thuộc cạnh $CA,AB$ sao cho $\angle HEC=\angle DCB$ và $\angle HFB=\angle DBC$. $M,N$ là đối xứng của $E,F$ qua $HC,HB$. Đường tròn $(HCM)$ và $(HBN)$ cắt nhau tại $K$ khác $H$. $L$ là tâm ngoại tiếp của tam giác $HEF$. Chứng minh rằng $HL\parallel KD$.

Bài toán 171 (Kiểm tra dự tuyển 10 THPT chuyên KHTN). Cho tam giác $ABC$ nhọn nội tiếp đường tròn $(O)$ và trực tâm $H$. Đường tròn đường kính $AH$ cắt $(O)$ tại $G$ khác $A$. Đường thẳng qua $A$ vuông góc với $GA$ cắt $OB,OC$ lần lượt tại $M,N$. $AH$ cắt $OB,OC$ theo thứ tự tại $P,Q$. $MQ$ cắt $NP$ tại $R$. Chứng minh rằng $AR$ song song đường thẳng Euler của tam giác $ABC$.

Lời giải của Việt(vietdohoangtk7nqd) có ý hay nhưng trình bày không cẩn thận, em chú ý rằng trong lời giải em đưa lên có 2 điểm $M$, có thời gian thầy sẽ trình bày lại giúp em. Mình đưa ra đáp án cho bài toán 147.

Đáp án bài toán 147. Chú ý rằng $M,N$ lần lượt là nghịch đảo của $C,B$ qua đường tròn $(AEF)$. Sử dụng phép nghịch đảo cực $A$ phương tích bất kỳ ta đưa về bài toán sau

Mình xin đề nghị tiếp một bài nữa cho topic duy trì hai bài

Bài toán 157. Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$ với tâm nội tiếp $I$. Đường tròn $(K)$ tiếp xúc $CA,AB$ và tiếp xúc trong $(O)$. $M,N$ nằm trên $AO$ sao cho $\angle ABM=\angle ICB$ và $\angle ACN=\angle IBC$. Gọi $L$ là tâm ngoại tiếp tam giác $IMN$. $AL$ cắt $(O)$ tại $D$ khác $A$. $DI$ cắt $(O)$ tại $G$ khác $D$. Chứng minh rằng $\angle AGK=90^\circ$.

Cám ơn Hoàng và Dương đã đóng góp lời giải. Bài toán này xuất phát từ đây. Trong đó có hai lời giải khác nhau, tuy nhiên thầy giải dựa trên bài Tuymaada 2009.

Xin đề nghị bài toán tiếp.

Bài toán 147. Cho tam giác $ABC$ nhọn có trực tâm $H$. $E,F$ lần lượt thuộc đoạn $CA,AB$ sao cho $EF$ tiếp xúc $(BHC)$. $K$ là tâm ngoại tiếp tam giác $AEF$. $M,N$ lần lượt thuộc đoạn $KC,KB$ sao cho $\angle KME=\angle KEC,\angle KNF=\angle KFB$. Chứng minh rằng $(AMN)$ tiếp xúc $EF$.

Topic này bị gián đoạn một chút vì bài này, thực sự mình mong muốn tìm lời giải không nghịch đảo cho nó nhưng xem ra khó có lời giải khác. Vậy mình sẽ đưa ra lời giải nghịch đảo của mình. Trước hết ta xử lý bài toán một chút.

Giải bài toán 124. Gọi $J$ là trung điểm $EF$ và $L$ là đối xứng của $A$ qua $OT$ thì $L$ thuộc $(O)$ và $AL$ là đường đối trung. $(S)$ là đường tròn ngoại tiếp $(AQL)$. Do đó $(Y)$ là đường tròn qua $A,J$ và trực giao với $(AQL)$. Gọi $R$ đối xứng $A$ qua $BC$ thì $(Z)$ là đường tròn qua $A,R$ và trực giao với $(AQD)$. Ta biết bài toán quen thuộc là $DP$ đồng quy với $BC$ và đường nối tiếp điểm $M,N$ của $(K)$ với $CA,AB$, gọi điểm đồng quy là $G$. Vậy ta có thể xác định $Q$ bằng cách cho $MN$ cắt $BC$ tại $G$ và $GD$ cắt $(K)$ tại $Q$. Đến đây ta chú ý rằng đường tròn $(ADI)$ luôn trực giao với $(O)$ nên tâm của $(ADI)$ luôn nằm trên $AT$. Do đó ta chỉ cần chứng minh tâm của $(ADI)$ nằm trên $YZ$ nữa thì hiển nhiên giao điểm $X$ của $YZ$ và $AT$ là tâm của $(ADI)$. Việc chứng minh tâm của $(ADI)$ nằm trên $YZ$ tương đương với việc ta cần chứng minh các đường tròn $(Y),(Z),(AID)$ đồng trục.

Nghịch đảo cực $A$ phương tích bất kỳ và sử dụng ký hiệu tương tự đồng thời viết lại bài toán với đường tròn nội tiếp, ta thu được bài toán sau

Bài toán 124'. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,M,N$. Đường tròn $(AMN)$ cắt $(O)$ tại $G$ khác $A$. Đường tròn $(ADG)$ cắt $(I)$ tại $Q$ khác $D$.  $L$ là trung điểm $BC$. $(K)$ là đường tròn tiếp xúc $CA,AB$ và tiếp xúc trong $(O)$. $y$ là đường thẳng qua $K$ vuông góc với $QL$ và $z$ là đường thẳng qua $O$ vuông góc với $QD$. Chứng minh rằng $y,z$ và $ID$ đồng quy.

Bài toán 124' đã được giải chi tiết tại đây http://artofproblems...c6t48f6h1368124

Để topic tiếp tục mình xin đề nghị một bài toán sau khá đơn giản

Bài toán 125 (Đề thi Ba Lan). Cho ngũ giác lồi $ABCDE$ với $BC=DE$ và $\angle ABE=\angle CAB=\angle AED-90^\circ$ và $\angle ACB=\angle ADE$. Chứng minh rằng $BCDE$ là hình bình hành.

Mình xin đề nghị bài tập tiếp cho topic được liên tục.

Bài toán 119. Cho tam giác $ABC$ có trực tâm $H$ và tâm ngoại tiếp $O$. $E,F$ là trung điểm $CA,AB$. Các điểm $M,N$ thuộc $OH$ sao cho $FM\parallel AC$, $EN\parallel AB$. $K$ là điểm thuộc $BC$ sao cho $\angle HKB=\angle OKC$. $OK$ cắt $FM,EN$ lần lượt tại $P,Q$. $MQ$ cắt $PN$ tại $R$. Chứng minh rằng $AH,OR,BC$ đồng qui.

Bảo đồng ý, mình đề nghị một bài sau

$\boxed{\text{Bài toán 45.}}$ Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và tâm nội tiếp $I$. Đường tròn $(K)$ tiếp xúc $CA,AB$ tại $E,F$ và tiếp xúc trong $(O)$ tại $D$. Gọi $M,N$ là tâm ngoại tiếp tam giác $ADE,ADF$. Trung trực $CA,AB$ cắt $BC$ tại $S,T$. Trên trung trực $IA$ lấy các điểm $P,Q$ sao cho $SP\parallel AC$ và $TQ\parallel AB$. Chứng minh rằng $MP,NQ$ và $AO$ đồng quy.

Rất mong topic sẽ sôi nổi, tiến tới nếu đạt mốc 100 bài nên ra một ấn phẩm nhỏ kỷ niệm !

Cám ơn Dương đã nhắc lại một mở rộng cũ, mở rộng này còn có phát triển hơn nữa khi thay thế các đường vuông góc như sau

http://artofproblems...nity/q2h1140524

Lời giải trong topic đó của Luis dùng nghịch đảo và tỷ số kép.

Ủng hộ ý kiến của viet nam in my heart, chúng ta nên dành thêm chút thời gian để đọc và phản biện lời giải đưa lên.

Lời giải bài toán 40.

Ta sẽ chứng minh $AL$ và $DK$ cùng vuông góc với $OG$ thì $ADKL$ là hình bình hành, thật vậy. Đường thẳng qua $P$ vuông góc $OP$ cắt $BC,AD$ tại $S,T$. Theo bài toán con bướm thì $P$ là trung điểm $ST$. Gọi $BC$ cắt $AD$ tại $H$. Theo tính chất điểm Miquel dễ thấy tứ giác $ABGH$ nội tiếp nên $\angle BGA=\angle BHA$ và $\angle GBA=180^\circ-\angle GAH=\angle HTS$. Từ đó hai tam giác $GBA$ và $HTS$ đồng dạng g.g. Chú ý $GQ$ là đường cao của tam giác $GBA$ nên nếu gọi $HW$ là đường cao tam giác $HTS$ nên $\frac{PG}{ST}=\frac{HW}{ST}=\frac{GQ}{AB}$. Từ đó suy ra $\frac{GP}{GQ}=\frac{ST}{AB}=\frac{AL}{AE}$. Gọi $M$ là hình chiếu của $G$ lên $PQ$ và $N$ là hình chiếu của $A$ lên $EL$. Do $EA\perp QG,EL\perp PQ$ nên hai tam giác vuông $ANE$ và $GMQ$ đồng dạng. Suy ra $\frac{AN}{GM}=\frac{AE}{GQ}=\frac{AL}{GP}$, từ đó hai tam giác vuông $ALN$ và $GPM$ đồng dạng, suy ra $AL\perp GP$.

$\boxed{\text{Bài toán 41.}}$ Cho tam giác $ABC$ có $P,Q$ là hai điểm đẳng giác. $K,L$ là tâm đường tròn $(PBC),(QBC)$. $PK,QL$ lần lượt cắt trung trực $AP,AQ$ tại $M,N$. $E,F$ là hình chiếu của $M$ lên $CA,AB$. $G,H$ là hình chiếu của $N$ lên $CA,AB$. Chứng minh rằng $E,F,G,H$ cùng thuộc một đường tròn và đường tròn này luôn tiếp xúc một đường thẳng cố định khi $P,Q$ thay đổi.

Cấu hình của bài thầy Hà trong bài đề nghị của Khánh là cấu hình rất thú vị, trên đó khai thác được khá nhiều điểm đặc biệt các tam giác $AA_bA_c,BB_cB_a,CC_aC_b$ mà những tâm đặc biệt của tam giác tạo bởi các tâm trên nằm trên đường thẳng $OI$ của $ABC$.

Mình ví dụ một bài như sau

Giữ nguyên đề của Khánh. Gọi $O_a,O_b,O_c$ là tâm ngoại tiếp tam giác $AA_bA_c,BB_cB_a,CC_aC_b$. Chứng minh rằng trọng tâm tam giác $O_aO_bO_c$ nằm trên đường thẳng $OI$ của $ABC$.

Bài toán 61 lời giải trên báo dùng phương tích cũng rất hay, lời giải này và của Quân (halloffame) đều khác với đáp án mình làm. Ai có thể đưa lời giải của báo lên không ?

Có một lưu ý nhỏ là bài toán 60 có nguồn gốc từ tạp chí Mathematical Reflections, sau đó nó được Telv Cohl tổng quát trên AoPS như sau

$\boxed{\text{Bài toán 60'.}}$ Cho tam giác $ABC$ nội tiếp $(O)$. Các đường tròn mixtilinear nội ứng với $A,B,C$ là $(O_a),(O_b),(O_c)$ lần lượt tiếp xúc $(O)$ tại $D,E,F$. $P$ nằm trên đường thẳng $OI$. $PD,PE,PF$ lần lượt cắt $(O_a),(O_b),(O_c)$ tại điểm thứ hai $X,Y,Z$. Chứng minh rằng $AX,BY,CZ$ đồng quy.

Trường hợp bài toán 60 là khi $P$ trùng $O$. Tuy nhiên bài toán tổng quát này khá khó, mình đưa lên là để cùng thảo luận, biết đâu có một lời giải hay cho bài này. Mặc dù vậy bài toán 60 gốc cũng đủ hay.

Bài toán 83 của Bảo có thể coi là trường hợp riêng của bài sau (sau khi viết lại cho tam giác $PBC$)

http://analgeomatica...2-thang-12.html

Thầy thử đề xuất một bài mới !

$\boxed{\text{Bài toán 84.}}$ Cho tam giác $ABC$ có đường cao $AD$. Trên tia $BC,CB$ lấy các điểm $G,H$ sao cho $BG=BA,CH=CA$. $E,F$ là trung điểm của $DG,DH$. Đường tròn $(A,AD)$ cắt $CA,AB$ tại $P,Q$. $M,N,Y,Z$ lần lượt đối xứng $A$ qua $C,B,P,Q$. $NE$ cắt đường tròn $(A,AD)$ tại $K$ sao cho $K,N$ khác phía đường thẳng qua $A$ vuông góc $KN$. $MF$ cắt đường tròn $(A,AD)$ tại $L$ sao cho $L,M$ khác phía đường thẳng qua $A$ vuông góc $LM$. Lấy $S,T$ thuộc $MF,NE$ sao cho $YS\parallel PL$ và $ZT\parallel QK$. Chứng minh rằng $D$ là tâm $(AST)$.

 

Lời giải khác cho bài toán 113. Gọi $Q$ đẳng giác với $P$ trong tam giác $ABC$ thì $M$ là hình chiếu của $Q$ lên $BC$. Dễ thấy $AQ\perp EF$ nên ta sẽ chứng minh $AQ\perp XK$ thì suy ra $EF\parallel XK$, thật vậy. Gọi $AP$ cắt $(O)$ ngoại tiếp tam giác $ABC$ tại $Y$ khác $A$. Gọi đường thẳng qua $L$ song song $BC$ cắt $CA,AB$ tại $Z,T$. Ta thấy $\angle PTZ=\angle PFE=\angle PAE=\angle YBC$ và $\angle PZT=\angle PEF=\angle PAB=\angle YCB$ do đó hai tam giác $PZT$ và $YCB$ đồng dạng có đường cao tương ứng là $PL,YK$. Từ đó $\frac{LZ}{LT}=\frac{KC}{KB}$ nên $A,L,K$ thẳng hàng. Từ đó theo bài toán Tuần 1 tháng 4/2016 ta có $AQ\perp XK$. Ta hoàn thành chứng minh.

Cám ơn Hoàng đã đóng góp lời giải và bài toán mới.

Bài toán này thực chất là một kết quả kinh điển. Chứng minh cực trực giao của một đường thẳng đi qua tâm ngoại tiếp nằm trên đường tròn Euler. Mình xin đưa ra một chứng minh ngắn gọn như sau. Viết bài toán theo ký hiệu điểm.

Bài toán. Cho tam giác $ABC$ có tâm ngoại tiếp $O$. $d$ là đường thẳng đi qua $O$. $D,E,F$ là hình chiếu của $A,B,C$ lên $d$. Chứng minh rằng đường thẳng qua $D,E,F$ vuông góc với $BC,CA,AB$ đồng quy trên đường tròn Euler của $ABC$.

Lời giải. Gọi $l$ là đường thẳng qua trực tâm $H$ của $ABC$ và vuông góc với $d$. Gọi $S$ là điểm anti-Steiner của $l$. $K$ đối xứng $H$ qua $BC$ thì $K$ thuộc $(O)$. Do $S$ là điểm anti-Steiner của $l$ nên $T$ đối xứng $S$ qua $BC$ nằm trên $l$. Từ đó gọi $ST$ cắt $(O)$ tại $X$ khác $S$ thì theo tính đối xứng ta có $\angle AXS=\angle AKS=\angle KHT$ do đó $AX\parallel HT\perp d$ nên $AX$ đi qua $D$ hay $D$ là trung điểm $AX$. Từ đó đường thẳng qua $D$ vuông góc $BC$ đi qua trung điểm $G$ của $SH$. Tương tự các đường thẳng còn lại đi qua $G$ và dễ thấy $G$ nằm trên đường tròn Euler của $ABC$.

Bài toán 100. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, trực tâm $H$. $MN$ và $PQ$ là hai dây cung vuông góc với nhau tại điểm $S$. Gọi giao điểm của đường thẳng Simson ứng với $M,N$ của tam giác $ABC$ là $K$. Gọi giao điểm của đường thẳng Simson ứng với $P,Q$ của tam giác $ABC$ là $L$. Chứng minh rằng $K,L$ đối xứng nhau qua trung điểm $T$ của $HS$.

Bài toán 98. Cho tam giác $ABC$ giả sử có điểm $P$ nằm trong tam giác sao cho $\angle PBA=\angle PCA$ đồng thời nếu có các đường tròn $(K)$ qua $P,C$ và đường tròn $(L)$ qua $P,B$ sao cho $(K),(L)$ cắt nhau tại $Q$ khác $P$ thì $BQ$ đi qua giao điểm $E$ của $(K)$ và $AC$ còn $CQ$ đi qua giao điểm $F$ của $(L)$ và $AB$. Chứng minh rằng $BE=CF$.

Nguồn gốc: http://www.cut-the-k.../Stoyanov.shtml

Lời giải bài 92 có ở đây http://artofproblems.../u68918h1283315

$\boxed{\text{Bài toán 93.}}$ Cho tam giác $ABC$ có điểm Fermat $F$. $FA,FB,FC$ cut $BC,CA,AB$ tại $X,Y,Z$. $FB,FC$ cắt $XZ,XY$ lần lượt tại $M,N$. Chứng minh rằng đường thẳng Euler của tam giác $AMN$ vuông góc với $BC$.

$\boxed{\text{Lời giải bài 16}}$: Lời giải của mình không được hay cho lắm

Dễ thấy chỉ cần chứng minh $QR \perp AG$ là xong

Gọi $X,Y$ lần lượt là điểm đối xứng của $A$ qua $Q,R$. Suy ra $B,M,X$ thẳng hàng và $C,N,Y$ thẳng hàng

Khi đó $QR$ là đường trung bình của tam giác $AXY$ nên $QR \parallel XY$ suy ra chỉ cần chứng minh $XY \perp AG$ 

Theo một bổ đề quen thuộc khi chứng minh định lý $Brocard$ thì ta có: $HL,EF,BC$ đồng quy tại $U$

                                                                                                                  $E,F,H,L$ đồng viên

                                                                                                                  $B,C,H,L$ đồng viên

Đường thẳng qua $A$ vuông góc với $AK$ cắt $BE,CF$ tại $T,F$

Do $HL,EF,BC$ đồng quy tại $U$ nên ta có chùm điều hòa cơ bản $H(STAL)=-1$ mà $ST \parallel HL$ nên $AS=AT$

Ta có:$ATBX,ASCY$ là hình bình hành nên suy ra $BXCY$ là hình bình hành suy ra $BY,CX$ cắt nhau tại trung điểm $Z$ của mỗi đường

Lời giải của viet nam in my heart rất hay nhưng để mình chỉnh lại một chút đoạn sau cho đẹp, không cần tích vô hướng.

Đến đoạn "$BY,CX$ cắt nhau tại trung điểm $Z$ của mỗi đường". (Chú ý $A$ là trung điểm $ST$ có thể dễ thấy qua bài toán con bướm)

Ta cần chứng minh hai tam giác $BZX$ và $LGA$ đồng dạng là xong vì đã có $LG\perp BZ,LA\perp BX$. Vậy ta cần cm $\frac{LG}{LA}=\frac{BZ}{BX}$ hay $\frac{LG}{LA}=\frac{BC}{ST}.$

Kẻ đường cao $HJ$ của $HST$ thì $LA=HJ$. Mặt khác từ $\triangle HST\sim\triangle LBC$ nên $\frac{AL}{ST}=\frac{HJ}{ST}=\frac{LG}{BC}$. Ta có đpcm.