Chủ đề này có 61 trả lời

[Viet Hoang 99]

$7/$ Cho tam giác $ABC$. $D;E;F$ lần lượt thuộc cạnh $BC;CA;AB$. $AD\cap CF\equiv M;AD\cap BE\equiv N;BE\cap CF\equiv P$

Biết $S_{MNP}=S_{AMF}=S_{BDN}=S_{CPE}=1$
Tính $S_{ABC}$

 

 

$7/$ 

Có: $S_{MNP}=S_{CPE}\Rightarrow S_{MNC}=S_{CEN}\Rightarrow ME//CN$

$\Rightarrow \frac{AM}{MN}=\frac{AE}{CE}\Rightarrow \frac{S_{AMN}}{S_{MNP}}=\frac{S_{APE}}{S_{CPE}}$

Mà $S_{MNP}=S_{CPE}$

$\Rightarrow S_{AMP}=S_{APE}$

$\Rightarrow S_{AFP}=S_{ACP}$ (Do $S_{AFN}=S_{CPE}$)

$\Rightarrow FP=CP$

$\Rightarrow S_{FBP}=S_{CBP}$

$\Rightarrow S_{FMNB}=S_{NPCD}$ (Do $S_{MNP}=S_{BND}$)

Cmtt ta có: $S_{FMNB}=S_{NPCD}=S_{AMPE}$

Đặt $S_{FMNB}=S_{NPCD}=S_{AMPE}=x$

Có $\frac{AM}{AN}=\frac{AE}{CE}$
Mà $\left\{\begin{matrix}\frac{AM}{MN}=\frac{S_{AMP}}{S_{MNP}}=\frac{x}{2}  &  & \\ \frac{AE}{CE}=\frac{S_{ABE}}{S_{CBE}}=\frac{2x+2}{x+2}  &  &  \end{matrix}\right.$

 

$\Rightarrow \frac{x}{2}=\frac{2x+2}{x+2}\Leftrightarrow x=\sqrt{5}+1$

$\Rightarrow S_{ABC}=3\sqrt{5}+3+4=3\sqrt{5}+7$

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 29-05-2014 - 12:36

[Viet Hoang 99]

$8/$ Cho lục giác $ABCDEF$ có các cạnh đối song song. Gọi $H;K$ là hình chiếu của $A;B$ trên $CE;DF$. Cm: $\frac{DF}{CE}=\frac{AH}{BK}$

 

$8/$

 

$AD\cap BE\equiv M;~~FC\cap AD\equiv N;~~BE\cap CF\equiv P$

Có: $S_{AED}=S_{BDE}$
$\Rightarrow $ $S_{AME}=S_{BMD}$

Cmtt ta có: $S_{BPF}=S_{CPE}$

và $S_{FND}=S_{ANC}$

Có: $S_{BFD}=$ $S_{MNP}$ + $S_{BPF}$ + $S_{FND}$ + $S_{BMD}$

$S_{AEC}=$ $S_{MNP}$ + $S_{AME}$ + $S_{CPE}$ + $S_{ANC}$
Từ trên suy ra 
$S_{BFD}=S_{AEC}$

$\Rightarrow DF.BK=AH.CE$
$\Rightarrow \frac{DF}{CE}=\frac{AH}{BK}$

(đpcm)

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 29-05-2014 - 13:03

[Phuong Mark]

 

 

 

$10/$

$a/$ Ta có $OI\bot PQ$ nên $I$ là điểm chính giữa cung $PQ\Rightarrow $ cung $PI$ = cung $IQ$

=> $\widehat{IPM}=\widehat{IPQ}, \widehat{IQM}=\widehat{IQP}$ do chắn 2 cung bằng nhau

=> IP và IQ là các tia phân giác => I là tâm dường tròn nội tiếp $\Delta MPQ$

b / OPMQ là hình vuông <=> $\widehat{POQ}=90^{\circ}$ =>$\widehat{POM}=45^{\circ}\Rightarrow OM=\frac{OP}{cosPOM}=\frac{R}{cos45^{\circ}}=R\sqrt{2}$

c / Gọi tâm đường tròn ngoại tiêp $\Delta MPQ$ là H, vì OPMQ nội tiếp nên H là tâm đường tròn

=> H trung điểm OM. Gọi N là trung điểm OA=> NH//BC [đường tb] => NH cố định=> H luôn di chuyển trên 1 đường thẳng cố định

 

Kẹp $ vào các điểm cho đẹp, như mình đã sửa

Bài làm phải có hình vẽ, trích dẫn, ghi STT bài, mình sửa tất cả trừ hình thì chưa đăng, bạn tự đăng hình lên đi, đã có hướng dẫn ở #1

 

Câu b: bạn thiếu trường hợp........chưa chứng minh tứ giác MPOQ$ là hình vuông

Câu C: $NH$ là đường trung bình của tam giác $OAM$ chứ bạn

 nhưng là vậy đi chăng nữa thì bạn cũng chưa thể suy ra được $NH?$ cố định

vậy $NH//BM$ thì $M$ là điểm cố định...... bạn

       

Còn đây là cách của mình

Câu b: ( cách 2)

 

giả sử $M$ là điểm trên đường thẳng $d$ sao cho tứ giác $MPOQ$ là hình vuông $\Rightarrow$  $MO= R \sqrt{2}$

$\Rightarrow$ $M$ nằm trên $(O;R \sqrt{2})$

$\Rightarrow$ $M$ là giao điểm của đường thẳng $(d)$ và $(O;R \sqrt{2})$ 

 

chứng minh điều giả sử trên :

vì: $OM=R \sqrt{2} > R$ $\Rightarrow$ $M$ nằm ngoài $(O;R)$ nên từ $M$ kẻ $2$ tiếp tuyến $MP$ và $MQ$ đến đường tròn 

Xét tam giác $MPO$ có :

$MP^{2}=MO^{2}-OP^{2}=R^{2}$ $\Rightarrow$ $MP=R$ 

tương tự ta cũng có: $MQ=R$ $\Rightarrow$ $MPOQ$ có $4$ cạnh bằng nhau và $1$ góc vuông là hình vuông

Câu C:

Từ $O$ kẻ đường thẳng vuông góc đến đường thẳng $(d)$ tại $K$ $\Rightarrow$  $K$ nằm trên đường tròn đường kính $OM$

$\Rightarrow$ Đường tròn ngoại tiếp tam giác $MPQ$ đi qua $2$ điểm cố định là $O$ và $K$ 

$\Rightarrow$ Tâm đường tròn ngoại tiếp tam giác $MPQ$ chạy trên đường trung trực của đoạn thẳng $OK$ cố định ( vì $AB$ cố định)

Bài viết đã được chỉnh sửa nội dung bởi Phuong Mark: 29-05-2014 - 21:04

[killerdark68]

$21/$
Cho ΔABC nội tiếp đường tròn tâm O,đường cao BE,AD,CQ cắt tai H,đường kính AF, trung điểm M của BC,Trọng tâm G của ΔABC .N,P,I,K,L lần lượt là trung điểm của AB,AC,HA,HB,HC.CMR:
a,3 điểm H,G,O thẳng hàng và HG=2OG.
b,các đường thẳng đi qua M,N,P song song OA,OC,OB đồng quy
c, CMR 9 điểm M,N,P,I,K,L,D,E,Q cùng thuộc đường tròn .Tính bán kính đường tròn đó
d,CM bán kính đường tròn ngoại tiếp các Δ HAB,HAC,HBC = nhau
e, cho biết BC cố định,A di động.CM H ∈ 1 đường tròn cố định và xác định vị trí điểm A để HD max
$22/$
Cho BC la dây cung cố định của đường tròn tâm O bán kính R (BC khác 2R).A là điểm chuyển động trên cung lớn BC.Vẽ hình bình hành ABCD . E la điểm đối xứng của C qua B.
a,Xác định vị trí của A để:
1,P_ABCD max
2,S_{ABCD max}
3,AE max,AEmin
b,CM trung điểm F của đoạn thẳng EA $\in$ 1 đường cố định
c,CM D $\in$ 1 đường cố định
d,Xác định vị trí của A để BD max,BD min
e,Gọi G la điểm đối xứng của O qua B.,Xác định vị trí của A để GA+2EA min

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 08-07-2014 - 07:10

[nguyenhongsonk612]

15) Gọi $A,B,C$ là góc của tam giác $ABC$.

Tìm điểu kiện của tam giác $ABC$ để biểu thức :

$P=sin \frac{A}{2} sin \frac{B}{2} sin \frac{C}{2}$

đạt giá trị lớn nhất . Tìm giá trị lớn nhất ấy?

Lời giải:

Vẽ như hình bên:

Đặt: $BC=a;CA=b;AB=c$

Ta có:

$sin\frac{A}{2}=\frac{BH}{AB}\leq \frac{BI}{c}$

$sin\frac{A}{2}=\frac{CK}{AC}\leq \frac{CI}{b}$

$\Rightarrow 2.sin\frac{A}{2}\leq \frac{a}{b+c}$

Tương tự ta cũng có: $2.sin\frac{B}{2}\leq \frac{b}{a+c}$ và $2.sin\frac{C}{2}\leq \frac{c}{a+b}$

$\Rightarrow P\leq \frac{abc}{8(a+b)(b+c)(c+a)}$

Theo BĐT Cô-si ta có:

$a+b\geq 2\sqrt{ab};b+c\geq 2\sqrt{bc};c+a\geq 2\sqrt{ca}$

$\Rightarrow (a+b)(b+c)(c+a)\geq 8abc$

$\Rightarrow P\leq \frac{abc}{64abc}=\frac{1}{64}$

Vậy $max P=\frac{1}{64}$. Dấu "=" $\Leftrightarrow a=b=c\Leftrightarrow \Delta ABC$ đều

Hình gửi kèm

• 

[thuydung2000]

$23/$

Cho tam giác ABC có 2 đường cao BB' và CC' cắt nhau tại H,trung tuyến AI. Đường thẳng vuông góc với AC tại A và đường thẳng vuông góc với AB tại A cắt CC' và BB' lần lượt tại M và N. Chứng minh rằng MN vuông góc với AI.

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 07-07-2014 - 15:48

[Viet Hoang 99]

$9/$ Cho $\Delta ABC$, $D,E$ di động trên tia $BA,CA$ sao cho $BD=EC$.

a) Vẽ hình bình hành $BDEM$. Tim tập hợp điểm $M$

b) Tìm vị trí $D,E$ để $DE$ min

$9/$

 

$a/$

Có: $\widehat{ECM}=\frac{180^o-\widehat{MEC}}{2}=\frac{180^o-\widehat{BAC}}{2}$ không đổi

$\Rightarrow M$ luôn thuộc $CM$

 

$b/$ $DE=BM_{min}$ khi $BM$ vuông góc $CM$

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 05-07-2014 - 21:03

[Trang Luong]

$9/$

h.png

 

$a/$

Có: $\widehat{EMC}=\frac{180^o-\widehat{MEC}}{2}=\frac{180^o-\widehat{BAC}}{2}$ không đổi

$\Rightarrow M$ luôn thuộc $CM$

 

$b/$ $DE=BM_{min}$ khi $BM$ vuông góc $CM$

Vì $\Delta ABCconst$. Giả sử $AB<AC$. Khi $A\equiv D\Rightarrow DE=AC-ABconst\Rightarrow min DE=AC-AB$

Chả nhẽ có gì sai sót chăng. ??? 

Bài này trích trong NCPT lớp 9 hay 8 . Chả nhẽ đầu bài có vấn đề

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 05-07-2014 - 21:17

[nguyenhongsonk612]

Vì $\Delta ABC$ $const$. Giả sử $AB<AC$. Khi $A\equiv D\Rightarrow DE=AC-ABconst\Rightarrow min DE=AC-AB$

Chả nhẽ có gì sai sót chăng. ??? 

Bài này trích trong NCPT lớp 9 hay 8 . Chả nhẽ đầu bài có vấn đề

Kí hiệu này là gì thế TL? 

 

"hằng"

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 05-07-2014 - 22:03

[Viet Hoang 99]

 

 

17) Cho tam giác nội tiếp trong $(O;R)$ với $BC=a,AC=b,Ab=c$. lấy điểm $I$ bất kì ở phía trong tam giác và gọi $x,y,z$ lần lượt là khoảng cách từ $I$ đến $BC,AC,AB$.

chứng minh: $\sqrt {x}+\sqrt{y}+\sqrt{z} \leq \sqrt{ \frac{a^{2}+b^{2}+c^{2}}{2R}}$

 

 

$17/$

 

Áp dụng công thức

$S=\frac{abc}{4R}$
$\Rightarrow 2S=\frac{abc}{2R}$

$\Rightarrow \frac{a^2+b^2+c^2}{2R}=\frac{2S(a^2+b^2+c^2)}{abc}$

$=\frac{(ax+by+cz)(a^2+b^2+c^2)}{abc}$
$\geq \frac{(ax+by+cz)(ab+bc+ca)}{abc}$

$=\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right).(ax+by+cz)$

$\geq \left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)^2$ (BĐT BCS)

$\Rightarrow \sqrt{x}+\sqrt{y}+\sqrt{z}\leq \sqrt{\frac{a^{2}+b^{2}+c^{2}}{2R}}$

Dấu $=$ xảy ra khi: tam giác $ABC$ đều, $I$ là tâm đường tròn nội tiếp.

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 07-07-2014 - 15:44

[Viet Hoang 99]

 

18) Cho $(O;R)$ và 2 điểm A,B nằm ở ngoài $(O)$ với $OA=OB=2R$ và $OA$ vuông góc với $OB$ . Xác định vị trí của $M$ thuộc $(O)$ sao cho biểu thức : $P=MA+2MB$ đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất ấy?

 

$18/$

 

Lấy $C$ là trung điểm $OA$

$D$ là trung điểm $OC$

Ta có:

$\bigtriangleup OMD\sim \bigtriangleup OAM~~~(c-g-c)$

$\Rightarrow AM=2DM$

Khi đó $P=MA+2MB=2(MD+MB)\geq 2DB$ không đổi

Dấu = xảy ra khi: $M$ là giao điểm của $BD$ và $(O)$

 

Vậy $P_{Min}=2DB=2.\sqrt{OB^2+OD^2}=2.\sqrt{4R^2+\frac{1}{4}.R^2}=R\sqrt{34}$

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 21-07-2014 - 07:17

[phamanhtuan99]

 

$21/$
Cho ΔABC nội tiếp đường tròn tâm O,đường cao BE,AD,CQ cắt tai H,đường kính AF, trung điểm M của BC,Trọng tâm G của ΔABC .N,P,I,K,L lần lượt là trung điểm của AB,AC,HA,HB,HC.CMR:
a,3 điểm H,G,O thẳng hàng và HG=2OG.
 

$21/$

$a/$

 

Kẻ đường kính $BK$ như hình vẽ

$\Rightarrow BK \perp KC$

Mà $OM \perp BC$

$\Rightarrow OM \parallel CK$

Mà do $M$ là trung điểm của $BC$ nên $OM=\frac{1}{2} BC$

Mặt khác ta sẽ chứng minh $OM=\frac{1}{2} AH$ bằng cách chứng minh $AH=CK$

Do $\widetilde{BC}+\widetilde{CK}=\widetilde{BK}=180^o$

$\rightarrow \widehat{BAC} + \widehat{CAK} = 90^o$

Mà $\widehat{BAC} + \widehat{HCA} = 90^o$

$\Rightarrow \widehat{CAK} = \widehat{HCA}$

$\Rightarrow CH $ // $AK$

Mà $AH$ //$CK$

$\Rightarrow AHCK$ là hình bình hành

$\Rightarrow AH=CK$

$\Rightarrow OM=\frac{1}{2} AH$

Ta lại có $AG=2GM$ (tính chất trọng tâm)

         Và $\widehat{OMA} = \widehat{DAM}$

nên $\Delta{HGA}\sim \Delta{OGM}$

nên $H$,$G$,$O$thẳng hàng và $HG=2GO$

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 07-07-2014 - 17:04

[phamanhtuan99]

$22/$
Cho BC la dây cung cố định của đường tròn tâm O bán kính R (BC khác 2R).A là điểm chuyển động trên cung lớn BC.Vẽ hình bình hành ABCD . E la điểm đối xứng của C qua B.
a,Xác định vị trí của A để:
1,P_ABCD max
2,S_{ABCD max}

 1,Ta thấy $P_{ABCD}= 2(AB+BC)$ Mà $BC$ cố định nên để $P_{ABCD}$ max thì $AB$ max khi và chỉ khi $AB$ là đường kính của đường tròn tâm $O$

2, Kẻ đường cao của hình bình hành $ABCD$ như hình vẽ gọi là $AH$ $\Rightarrow S_{ABCD} = AH\cdot BC$ mà $BC$ cố định nên để $S_{ABCD} $ max thì $AH$ max khi và chỉ khi $A$ là điểm chính giữa cung $BC$

Bài viết đã được chỉnh sửa nội dung bởi phamanhtuan99: 07-07-2014 - 17:07

[HungNT]

$21/$
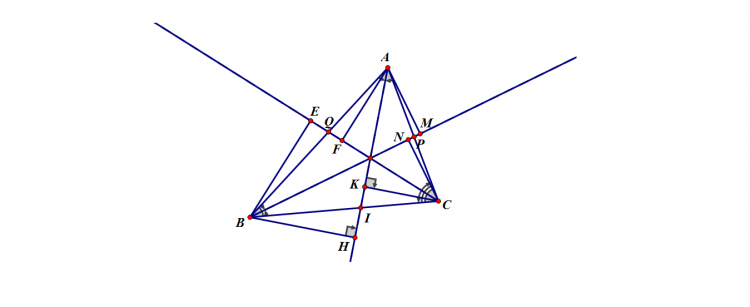
Cho ΔABC nội tiếp đường tròn tâm O,đường cao BE,AD,CQ cắt tai H,đường kính AF, trung điểm M của BC,Trọng tâm G của ΔABC .N,P,I,K,L lần lượt là trung điểm của AB,AC,HA,HB,HC.CMR:
a,3 điểm H,G,O thẳng hàng và HG=2OG.
b,các đường thẳng đi qua M,N,P song song OA,OC,OB đồng quy
c, CMR 9 điểm M,N,P,I,K,L,D,E,Q cùng thuộc đường tròn .Tính bán kính đường tròn đó

d,CM bán kính đường tròn ngoại tiếp các Δ HAB,HAC,HBC = nhau

e, cho biết BC cố định,A di động.CM H ∈ 1 đường tròn cố định và xác định vị trí điểm A để HD max 

b/ Ta gặp một bài toán quen thuộc, dễ dàng chứng minh $OA \bot QE$ bằng nhiều cách khác nhau

Gọi các đường thẳng song song trên lần lượt là $d_{1},d_{2},d_{3}$

Ta có $d_{1}//OA\Rightarrow d_{1} \bot QE$, mà $QM=EM=\frac{BC}{2}$

=>$d_{1}$ là trung trực QE

Chứng minh tương tự ta có d₂ trung trực DE và d₃ trung trực QD

=>  d₁,d₂ và d₃ đồng quy do là các đường trung trực của tam giác QED

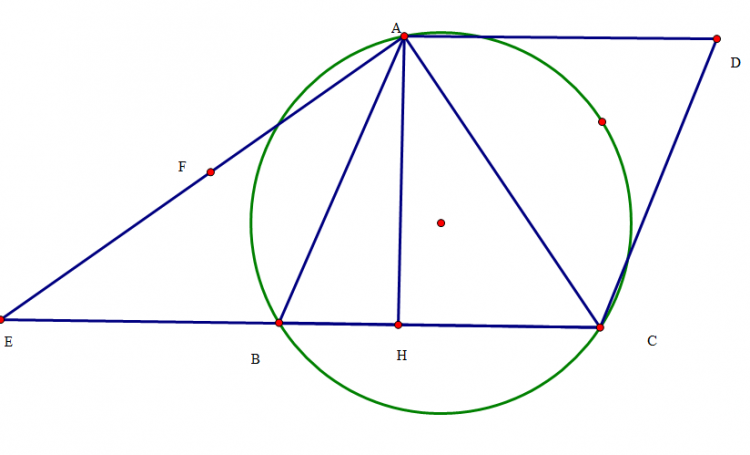
c/ Dựa vào tính chất đường trung bình tam giác ta dễ chứng minh NPLK và NILM là hình chữ nhật

=> N,P,L,K,I,M cùng thuộc đường tròn đường kính NL

$\Delta QNL$ vuông nên Q thuộc đường tròn đk NL

$\Delta KEP$ vuông và $\Delta IDM$ vuông nên D thuộc đường tròn đk MI và E thuộc dtdk KP

Vì IM,LN,KP đồng quy và $IM=LN=KP$ nên 9 điểm M,N,P,I,K,L,D,E,Q cùng thuộc 1 đường tròn

Đường tròn này là đường tròn Euler hay còn gọi là đường tròn chín điểm

d/ Áp dụng CT $S=\frac{abc}{4R}\Rightarrow R=\frac{abc}{4S}$

 

$R_{\left ( AHB \right )}=\frac{AH.HB.AB}{2HQ.AB}=\frac{AH.HB}{2HQ}$

 

và $R_{\left ( BHC \right )}=\frac{HB.HC}{2HD}$

 

mà $\frac{AH}{2HQ}=\frac{HC}{2HD}\left ( \Delta AHQ\sim \Delta CHD \right )$

$\Rightarrow R_{\left ( AHB \right )}=R_{\left ( BHC \right )}$

Chứng minh tương tự ta có $R_{\left ( AHB \right )}=R_{\left ( BHC \right )}=R_{\left ( AHC \right )}$

e/ Tứ giác AQEH có  $\angle QHE=180^{\circ}-\angle A \Rightarrow \angle BHC=180^{\circ}-\frac{sdBC}{2}$ không đổi

=> H thuộc cung chứa góc .... cố định

$HD_{max}\Leftrightarrow$ H điểm chính giữa cung $\Leftrightarrow A$ chính giữa cung BC lớn

HÌnh phức tạp dữ 

Bài viết đã được chỉnh sửa nội dung bởi HungNT: 08-07-2014 - 13:54

[phamanhtuan99]

14) Cho tứ giác $ABCD$ có $AB=AD$ và $CB=CD$

1, Chứng minh rằng:

a, Tứ giác $ABCD$ ngoại tiếp được một đường tròn

b, Tứ giác $ABCD$ nội tiếp được trong một đường tròn khi và chỉ khi $AB$ và $BC$ vuông góc với nhau.

Bài 14,1,a :

Do $AB=AD$ và $BC=BD$ nên $AC$ là trung trực của $BD$

Khi đó $AC$ là tia phân giác $\widehat{BAD}$ và $CA$ là phân giác $\widehat{BCD}$

nên tia phân giác hai góc này trùng nhau và chình là $AC$

gọi giao điểm của tia phân giác góc $D$ và góc $B$ của tứ giác $ABCD$ với AC lần lượt là $H$ và $K$ thì

$\frac{AH}{HC} = \frac{AD}{DC} = \frac{AB}{BC} = \frac{AK}{KC}$

 từ đó suy ra bốn tia phân giác bốn góc của tứ giác $ABCD$ đồng quy tại một điểm nên tứ giác này ngoại tiếp

Bài 14,1,b:

Ta thấy theo ý a ta cũng có $AC$ trung trực của $BD$ nên khi $AB \perp BC$ thì $IA \cdot IC = IB^2$

Mà ta dễ dang cm được $AD \perp DC$ và cũng có $IA \cdot IC = ID^2$

từ đó suy ra $IA \cdot IC =ID \cdot IB$ và tứ giác $ABCD nội tiếp

[Viet Hoang 99]

 

 

12) Cho đường tròn $(O)$ đường kính $AB=2R$. Một điểm $M$ chuyển động trên đường tròn $(O)$ ( M khác A và B) . Gọi $H$ là hình chiếu vuống góc cảu $M$ trên đường kính $AB$.Vẽ đường tròn có tâm là $(M)$ và bán kính là $MH$.Từ $A$ và $B$ lần lượtker các tiếp tuyến $AD$ và $BC$ đến đường tròn (D và C là các tiếp điểm ).

1, Chứng minh rằng khi $M$ di chuyển trên đường tròn $(O)$ thì $AD+BC$ có giá trị không đổi.

2, Chứng minh rằng $CD$ là tiếp tuyến của đường tròn $(O)$.

3, Chứng minh với bất kì vị trí nào của $M$ trên đường tròn (O) luôn có bất đẳng thức $AD.BC \leq R^{2}$. Xác định vị trí của $M$ trên đường tròn $(O)$ để đẳng thức xảy ra.

4, Trên đường tròn $(O)$ lấy điểm $N$ cố định. Gọi $I$ là trung điểm của $MN$ và $P$ là hình chiếu vuông góc của $I$ trên $MB$ . Khi $M$ di chuyển trên $(O)$ thì $P$ chạy trên đường tròn nào?

 

 

$12/$

 

$1/$

Có: $AD+BC=AH+BH=AB$ không đổi

$2/$

$D;M;C$ thẳng hàng (tiên đề Ơ-clit)

Có: $\left\{\begin{matrix}\widehat{DMA}=\widehat{AMH}~~~ (t/c ~TT) & & \\ \widehat{AMH}=\widehat{MBA}~~(\textrm{phụ}~\widehat{MAH}) & & \end{matrix}\right.$

$\Rightarrow \widehat{DMA}=\widehat{MBA}$

$\Rightarrow CD$ là tiếp tuyến của $(O)$

$3/$

Có: $AD.BC=AH.BH=MH^2\leq MO^2=R^2$
Dấu $"="$ xảy ra khi: $M$ là điểm chính giữa cung $AB$

 

$4/$ (Ý này không muốn vẽ lại hình, thông cảm)

Lấy $T$ là trung điểm $AN$

Có: $IP//MA$ (Cùng vuông góc $MB$)
$\Rightarrow IT$ là đường trung bình tam giác $NMA$

$\Rightarrow P$ thuộc đường tròn đường kính $BT$ cố định. (trừ điểm $N$)

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 09-07-2014 - 07:41

[HungNT]

$23/$ Cho đường tròn $\left ( O \right )$ và đường thẳng $d$ ở ngoài $\left ( O \right )$, $E$ là hình chiếu của $O$ trên $d$. $M$ là một điểm di động trên $d$, kẻ tiếp tuyến $MA$, $MB$. Dựng $EC \bot MA$ và $ED \bot MB$.

a/ Chứng minh $AB$ luôn đi qua một điểm cố định

b/ $CD$ cắt $OE$ tại $F$. C/m $F$ là điểm cố định

[Viet Hoang 99]

Những bài đăng không ghi số thứ tự (STT) của bài toán sẽ bị xóa không báo trước!

_______________
Chúng ta cùng khai thác giả thiết chứng minh bài toán sau:

(Làm ý nào thì trích đề ý đó nhé!)

$24)$ Cho tam giác $ABC$ và một điểm $O$ nằm trong tam giác đó. Các tia $AO;BO;CO$ cắt các cạnh $BC;CA;AB$  theo thứ tự tại $M;N;P$. Cmr:
$1)$ $\frac{OM}{AM}+\frac{ON}{BN}+\frac{OP}{CP}=1$

$2)$ $\frac{OA}{AM}+\frac{OB}{BN}+\frac{OC}{CP}=2$

$3)$ $\frac{AM}{OM}+\frac{BN}{ON}+\frac{CP}{OP}\geq 9$
$4)$ $\frac{OA}{OM}+\frac{OB}{ON}+\frac{OC}{OP}\geq 6$

$5)$ $\frac{AM}{OA}+\frac{BN}{OB}+\frac{CP}{OC}\geq \frac{9}{2}$

$6)$ $\frac{OM}{OA}+\frac{ON}{OB}+\frac{OP}{OC}\geq \frac{3}{2}$

$7)$ Trong ba tỉ số $\frac{OA}{OM};\frac{OB}{ON};\frac{OC}{OP}$ có ít nhất một tỉ số không nhỏ hơn $2$ và ít nhất một tỉ số không lớn hơn $2$.

$8)$ $\frac{OA}{OM}.\frac{OB}{ON}.\frac{OC}{OP}\geq 8$

$9)$ $\frac{AM}{OM}.\frac{BN}{ON}.\frac{CP}{OP}\geq 27$

$10)$ $\frac{AM}{OA}.\frac{BN}{OB}.\frac{CP}{OC}\geq \frac{27}{8}$

$11)$ $\sqrt{\frac{OA}{OM}}+\sqrt{\frac{OB}{ON}}+\sqrt{\frac{OC}{OP}}\geq 3\sqrt{2}$

$12)$ $\sqrt{\frac{AM}{OA}}+\sqrt{\frac{BN}{OB}}+\sqrt{\frac{CP}{OC}}$

$13)$ $\sqrt{\frac{OM}{AM}}+\sqrt{\frac{ON}{BN}}+\sqrt{\frac{OP}{CP}}$

$14)$ Xác định vị trí của điểm $O$ để $OA.BC+OB.CA+OC.AB$ đạt giá trị nhỏ nhất.

$15)$ Đặt $BC=a;CA=b;AB=c$ và gọi $d_a;d_b;d_c$ tương ứng là các khoảng cách từ $O$ đến các cạnh $BC;CA;AB$. Xác định vị trí điểm $O$ để:
$a)$ Tích $d_a.d_b.d_c$ đạt giá trị lớn nhất.

$b)$ Tổng $\frac{a}{d_a}+\frac{b}{d_b}+\frac{c}{d_c}$ đạt giá trị nhỏ nhất.

Bài viết đã được chỉnh sửa nội dung bởi Viet Hoang 99: 28-08-2014 - 20:41

[HungNT]

$24)$ Cho tam giác $ABC$ và một điểm $O$ nằm trong tam giác đó. Các tia $AO;BO;CO$ cắt các cạnh $BC;CA;AB$  theo thứ tự tại $M;N;P$. Cmr:

$1)$ $\frac{OM}{AM}+\frac{ON}{BN}+\frac{OP}{CP}=1$

$2)$ $\frac{OA}{AM}+\frac{OB}{BN}+\frac{OC}{CP}=2$

$3.\frac{AM}{OM}+\frac{BN}{ON}+\frac{CP}{OP}\geq 9$

1/

Dựng các đoạn OE,OF,GK song song với các cạnh như trên hình

OFBG là hbh nên $OG=FB$

$\frac{OM}{AM}=\frac{OG}{AB}=\frac{BF}{AB}$, $\frac{ON}{BN}=\frac{AE}{AB}$, $\frac{OP}{CP}=\frac{PE}{PA}=\frac{PF}{PB}$

 

$\frac{PE}{PA}=\frac{PF}{PB}=\frac{PE+PF}{PA+PB}=\frac{EF}{AB}$$=>\frac{OP}{CP}=\frac{EF}{AB}$

 

Từ đó $\frac{OM}{AM}+\frac{ON}{BN}+\frac{OP}{CP}=\frac{EA+FE+BF}{AB}=1$

2/

Từ cmt $1-\frac{OM}{AM}+1-\frac{ON}{BN}+1-\frac{OP}{CP}=\frac{AO}{AM}+\frac{BO}{BN}+\frac{CO}{CP}=2$

3/$\frac{AM}{OM}+\frac{BN}{ON}+\frac{CP}{OP}=\left (\frac{AM}{OM}+\frac{BN}{ON}+\frac{CP}{OP} \right )\left ( \frac{OM}{AM}+\frac{ON}{BN}+\frac{OP}{CP} \right )$

Do $\left ( a+b+c \right )\left ( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )\geq 9$ nên ta có đpcm 

Bài viết đã được chỉnh sửa nội dung bởi HungNT: 29-08-2014 - 14:50

[Phuong Mark]

13) Cho nửa đường tròn đường kính $AB$. Gọi $P$ là điểm chính giữa của cung $AB$, $M$ là điểm chuyển động trên cung $BP$. Trên đoạn $AM$ lấy điểm $N$ sao cho $AN=BM$.
1, Chứng minh tỉ số $\frac{NP}{MN}$ có giá trị không đổi khi điểm $M$ di chuyển trên cung $BP$. Tìm giá trị không đổi ấy?
2, Tìm tập hợ các điểm $N$ khi $M$ di chuyển trên cung $BP$ 
 
 
14) Cho tứ giác $ABCD$ có $AB=AD$ và $CB=CD$
1, Chứng minh rằng:
a, Tứ giác $ABCD$ ngoại tiếp được một đường tròn
b, Tứ giác $ABCD$ nội tiếp được trong một đường tròn khi và chỉ khi $AB$ và $BC$ vuông góc với nhau.
2, Giả sử $AB \perp BC$ . Gọi $(N)$ là đuờng tròn nội tiếp và $(M,R)$ là đường tròn khi tiếp tứ giác $ABCD$. Chứng minh:
a, $AB+BC=r+ \sqrt{r^{2}+4R^{2}}$
b, $MN^{2}=R^{2}+r^{2}-r \sqrt{r^{2}+4R^{2}}$
 
 
                                                                                    Bài làm
Bài 13: 
 
Câu 2:
 
                              Từ $N$ kẻ đường thẳng vuông góc với $AM$ cắt tiếp tuyến $Ax$ của đường tròn $(O)$ tại $G.$
                                                 $ \angle GAN = \angle ABM (= \frac{1}{2} sđ \widehat{AM})$
 
                                           Xét $\Delta ANG$ vuông tại $N$ và $\Delta BMA$ vuông tại $M$ có :
                                                                $\angle GAN= \angle ABM(CMT)$
                                                                               $AN=BM(gt)$
                                                      $\Rightarrow$ $\angle ANG= \angle BMA$
                                                                     $ \Rightarrow $ $AG=AB$
                                                  mà $AB$ cố định  $ \Rightarrow  $ $AG$ cố định
                                      $\Rightarrow $ $N$ thuộc đường tròn đường kính $AG$ cố định 
         $\Rightarrow$ Quỹ tích của điểm $N$ khi $M$ di chuyển trên cung $\widehat{BP}$ là cung tròn $\widehat{AP}$
 
 
Bài 14:                                            Xin lỗi về đề bài câu 2 sai nha! Mình đã sửa  
Câu 2.
                                           Kẻ $NK \perp AB, MQ \perp AB, NH \perp BC, MP \perp BC$
 
                                                                Gọi độ dài cạnh $AB=x,BC=y$
 
  Ta sẽ chứng minh được :       $MN^{2}=KQ^{2}+HP^{2}= (BK-BQ)^{2}+(BP-BH)^{2}$ 
                                                          $= (r- \frac{x}{2})^{2}+( \frac{y}{2}-r)^{2}$
                                                            $=2r^{2}-r(x+y)+ \frac{x^{2}+y^{2}}{4}$
 
                                                                 mà : $x^{2}+y^{2}=4R^{2}$
                                                   $\Rightarrow$ $MN^{2}=2r^{2}-r(x+y)+R^{2}$
 
                                             Theo câu $b$ ta lại có : $AB+BC=r+ \sqrt{r^{2}+4r^{2}}$
 
                                                                  $\Rightarrow$ $DPCM$
 
                                                       @ Còn  bài 16 mai mình post tiếp

 Mình nói thật là bài toán hình mình mượn trong quyển tài liệu sai nhiều quá!

Hình gửi kèm

• 
• 

Bài viết đã được chỉnh sửa nội dung bởi buiminhhieu: 31-08-2014 - 08:40