Trò chơi và bài toán về rubik
Hân cầm cục rubik đưa cho Kiên và khoe: "Xem này tớ xoay đủ 6 mặt hết chưa đầy một phút!".
Kiên cầm cục rubik đã hoàn thành 6 mặt ngắm nghía hồi lâu rồi nghĩ ra một "kế". Kiên lấy bút vẽ lên tất cả các mặt của rubik mỗi mặt gồm những mũi tên cùng chiều ở mỗi ô, duy nhất mặt màu đỏ thì Kiên vẽ mũi tên ở ô chính giữa vuông góc với các mũi tên ở xung quanh (Xem hình a) rồi đem đố Hân làm sao xoay lại cho đúng chiều.
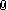rubik.png
a) Hân có xoay rubik được theo yêu cầu của Kiên không? Vì sao?
b) Nếu Kiên vẽ mũi tên như hình b) thì Hân có xoay lại được không? Hãy chỉ cho Hân cách xoay rubik lại trong trường hợp này nếu bạn giải được!
c) Ta gọi các mặt rubik là $a,b,c,d,e,g$ mỗi phép xoay sẽ được ký hiệu là $+, - , 2$ và được viết như là chỉ số của mặt ("+" tương ứng với xoay $+90^{\circ}$, "-" là xoay $-90^{\circ}$ còn $2$ là xoay $180^{\circ}$). Ta được tập hợp mẫu $E$:
$$E=\{a_+,a_-,a_2,...,g_+,g_-,g_2\}$$
$L$ là một dãy hữu hạn các phần tử $L=\{x_1,x_2,...,x_k\}$ trong đó $x_i\in E, \forall i=\overline{1,k}$ được gọi là dãy lệnh
Chứng minh rằng tồn tại một số tự nhiên $n$ để sau khi áp dụng $n$ lần liên tiếp dãy lệnh $L$, rubik sẽ trở lại trạng thái ban đầu!
Mình xin đóng góp một cách chứng minh khác cho câu $c$, tuy dài dòng hơn nhưng cũng dễ hiểu hơn.
Xét khối rubik $ABCD.A'B'C'D'$ gồm $27$ khối nhỏ, trong đó có $26$ khối có ít nhất $1$ mặt được tô màu, chia ra như sau :
+ $8$ khối ở đỉnh (tạm gọi là $8$ viên đỉnh), mỗi viên đỉnh có $3$ mặt được tô màu.
+ $12$ khối ở cạnh (tạm gọi là $12$ viên cạnh), mỗi viên cạnh có $2$ mặt được tô màu.
+ $6$ khối ở tâm các mặt, mỗi khối này chỉ có $1$ mặt được tô màu.
Nhận xét rằng khi thực hiện bất kỳ dãy lệnh nào thì các khối ở tâm các mặt chỉ có thể xoay chứ không thay đổi vị trí nên ta không cần quan tâm đến chúng.
Trước hết ta chứng minh rằng với mỗi viên đỉnh và mỗi dãy lệnh $L$ bất kỳ cho trước, tồn tại số tự nhiên $m> 0$ sao cho sau khi thực hiện $m$ lần liên tiếp dãy lệnh $L$ thì viên đỉnh đó trở lại đỉnh ban đầu.
Không làm mất tính tổng quát, ta chỉ cần xét viên đỉnh có vị trí ban đầu ở đỉnh $A$, có mặt hướng về phía ta màu đỏ, mặt trên màu xanh, mặt bên trái màu vàng.Ta gọi viên đỉnh này là $\alpha$ và trạng thái ban đầu của nó là $A_{V/Đ}^{X}$ (nêu rõ vị trí và màu các mặt)
Giả sử $\alpha$ không bao giờ trở lại đỉnh $A$ sau khi thực hiện xong $k$ dãy lệnh $L$ bất kỳ ($\forall k\in \mathbb{N}^+$).
Ta gọi $F$ là tập hợp các đỉnh khác $A$ ($F=\left \{ B,C,D,A',B',C',D' \right \}$)
Sau dãy lệnh $L$ lần thứ nhất, $\alpha$ đến đỉnh $K$ ($K\in F$).Một viên đỉnh khác (tạm gọi là $\beta$) sẽ đến $A$.
Sau dãy lệnh $L$ lần thứ hai, $\beta$ sẽ đến $K$ nên $\alpha$ phải đến $M$ ($M\in F$ và $M\not\equiv K$).Một viên đỉnh khác ($\gamma$) sẽ đến $A$.
Sau dãy lệnh $L$ lần thứ ba, $\gamma$ sẽ đến $K$, $\beta$ sẽ đến $M$ nên $\alpha$ phải đến $N$ ($N\in F$ và $K,M,N$ khác nhau từng đôi một).Một viên đỉnh khác ($\delta$) sẽ đến $A$.
..........................................................................................
.........................................................................................
Sau dãy lệnh $L$ lần thứ bảy, $\zeta \rightarrow K,\varepsilon \rightarrow M,\epsilon \rightarrow N,\delta \rightarrow P,\gamma \rightarrow Q,\beta \rightarrow R$ nên $\alpha$ phải đến $S$ ($S\in F$ và $K,M,N,P,Q,R,S$ khác nhau từng đôi một).Một viên đỉnh khác ($\eta$) sẽ đến $A$.
Sau dãy lệnh $L$ lần thứ tám, $\eta \rightarrow K,\zeta \rightarrow M,\varepsilon \rightarrow N,\epsilon \rightarrow P,\delta \rightarrow Q,\gamma \rightarrow R,\beta \rightarrow S$ nên $\alpha$ "không còn chỗ để đi"
Vậy điều giả sử trên là sai và ta suy ra : Sau không quá $8$ dãy lệnh $L$ thì $\alpha$ phải trở lại đỉnh ban đầu (ta chưa xét màu của các mặt) (điều này cũng đúng với bất kỳ viên đỉnh nào)
Giả sử sau $m_{\alpha }$ dãy lệnh $L$ thì $\alpha$ trở lại đỉnh $A$ ($1\leqslant m_{\alpha }\leqslant 8$).Có $2$ trường hợp :
+ Nếu khi đó trạng thái của $\alpha$ là $A_{V/Đ}^{X}$ thì có nghĩa là sau $n_{\alpha }=m_{\alpha }$ dãy lệnh $L$, viên đỉnh $\alpha$ trở lại trạng thái ban đầu (về cả vị trí và màu các mặt)
+ Nếu khi đó trạng thái của $\alpha$ là $A_{X/V}^{Đ}$ hoặc $A_{Đ/X}^{V}$ thì tức là sau $n_{\alpha }=3m_{\alpha }$ dãy lệnh $L$, viên đỉnh $\alpha$ sẽ trở lại trạng thái ban đầu (vì các trạng thái này chỉ là trạng thái $A_{V/Đ}^{X}$ xoay quanh trục $AD'$ góc $\pm 120^o$)
Tương tự, với viên đỉnh $\beta, \gamma,...$ thì sau $n_{\beta },n_{\gamma },...$ dãy lệnh $L$, chúng cũng trở về trạng thái ban đầu.
Hoàn toàn tương tự, ta chứng minh được với mỗi viên cạnh và mỗi dãy lệnh $L$ bất kỳ, tồn tại số tự nhiên $m> 0$ sao cho sau khi thực hiện xong $m$ dãy lệnh $L$ thì viên cạnh ấy trở về cạnh ban đầu.
Bây giờ xét viên cạnh có vị trí ban đầu trên cạnh $AB$, mặt trên xanh, mặt hướng về ta đỏ.Gọi đó là viên cạnh $1$, trạng thái ban đầu là $AB_{Đ}^{X}$.Giả sử sau $m_{1}$ dãy lệnh $L$ thì vc $1$ trở về cạnh $AB$.Có $2$ trường hợp :
+ Nếu khi đó trạng thái của vc $1$ là $AB_{Đ}^{X}$ thì tức là sau $n_{1}=m_{1}$ dãy lệnh $L$ thì vc $1$ trở lại trạng thái ban đầu.
+ Nếu khi đó trạng thái của vc $1$ là $AB_{X}^{Đ}$ thì tức là sau $n_{1}=2m_{1}$ dãy lệnh $L$ thì vc $1$ trở lại trạng thái ban đầu.
Tương tự, với các viên cạnh $2,3,...,12$ thì sau $n_{2},n_{3},...,n_{12}$ dãy lệnh $L$ thì chúng cũng trở về trạng thái ban đầu.
Vậy nếu $n$ là bội số chung của $n_{\alpha },n_{\beta },...,n_{\eta },n_{1},n_{2},...,n_{12}$ (có vô số số $n$ như thế) thì sau khi thực hiện $n$ dãy lệnh $L$ liên tiếp, khối rubik sẽ trở lại trạng thái ban đầu.
Bài viết đã được chỉnh sửa nội dung bởi chanhquocnghiem: 07-07-2014 - 15:57
