Chủ đề này có 10 trả lời

[hoangtubatu955]

KÌ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH GIỎI QUỐC GIA 12 THPT.

Thời gian: 180P, môn: Toán.

Câu 1: Giải hệ phương trình:

 $\left\{\begin{matrix} 3x^3+2x^2=y\\ 3y^3+2y^2=z\\ 3z^3+2z^2=x \end{matrix}\right.$

Câu 2: Cho dãy số $(x_n)$ được xác định bởi:

       $x_1=\frac{1}{2}; x_{n+1}=\frac{2014+x_n}{2016-x_n}$ với mọi $n=1,2,...$.

a. Chứng minh rằng dãy $(x_n)$ có giới hạn và tính giới hạn đó.

b. Với mỗi số tự nhiên $n \ge 1,$ đặt $y_n=\frac{1}{2013n+2015} \sum_{k=1}^{n} \frac{1}{x_k-2014}.$ Tính $\lim y_n$

Câu 3: Cho 2 đường tròn $(C_1)$ và $(C_2)$ tiếp xúc ngoài nhau tại $M$. Tiếp tuyến chung ngoài $AB$, ($A$ thuộc $(C_1)$, $B$ thuộc $(C_2)$). Trên tia $Mx$ là tiếp tuyến chung của 2 đường tròn ( $Mx$ không cắt $AB$) lấy điểm $C$ khác $M$. Gọi $E,F$ lần lượt là giao điểm thứ 2 của $CA$ với $(C_1)$, $CB$ với $(C_2)$. Chứng minh rằng tiếp tuyến của $(C_1)$ tại $E$, tiếp tuyến của $(C_2)$ tại $F$ và $Mx$ đồng quy.

Câu 4: Cho số nguyên dương $n\ge 2.$ Chứng minh rằng $m=2n^2-1$ là số tự nhiên nhỏ nhất sao cho tồn tại $n$ số nguyên dương $a_1, a_2,...,a_n$ thỏa mãn đồng thời các điều kiện:

  i, $a_1<a_2<...<a_n=m$

  ii, Tất cả $n-1$ số $\frac{a_1^2+a_2^2}{2}, \frac{a_2^2+a_3^2}{2},...,\frac{a_{n-1}^2+a_n^2}{2}$ đều là các số chính phương.

[phamxuanvinh08101997]

 

KÌ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH GIỎI QUỐC GIA 12 THPT.

Thời gian: 180P, môn: Toán.

Câu 1: Giải hệ phương trình:

 $\left\{\begin{matrix} 3x^3+2x^2=y\\ 3y^3+2y^2=z\\ 3z^3+2z^2=x \end{matrix}\right.$

Câu 2: Cho dãy số $(x_n)$ được xác định bởi:

       $x_1=\frac{1}{2}; x_{n+1}=\frac{2014+x_n}{2016-x_n}$ với mọi $n=1,2,...$.

a. Chứng minh rằng dãy $(x_n)$ có giới hạn và tính giới hạn đó.

b. Với mỗi số tự nhiên $n \ge 1,$ đặt $y_n=\frac{1}{2013n+2015} \sum_{k=1}^{n} \frac{1}{x_k-2014}.$ Tính $\lim y_n$

Câu 3: Cho 2 đường tròn $(C_1)$ và $(C_2)$ tiếp xúc ngoài nhau tại $M$. Tiếp tuyến chung ngoài $AB$, ($A$ thuộc $(C_1)$, $B$ thuộc $(C_2)$). Trên tia $Mx$ là tiếp tuyến chung của 2 đường tròn ( $Mx$ không cắt $AB$) lấy điểm $C$ khác $M$. Gọi $E,F$ lần lượt là giao điểm thứ 2 của $CA$ với $(C_1)$, $CB$ với $(C_2)$. Chứng minh rằng tiếp tuyến của $(C_1)$ tại $E$, tiếp tuyến của $(C_2)$ tại $F$ và $Mx$ đồng quy.

Câu 4: Cho số nguyên dương $n\ge 2.$ Chứng minh rằng $m=2n^2-1$ là số tự nhiên nhỏ nhất sao cho tồn tại $n$ số nguyên dương $a_1, a_2,...,a_n$ thỏa mãn đồng thời các điều kiện:

  i, $a_1<a_2<...<a_n=m$

  ii, Tất cả $n-1$ số $\frac{a_1^2+a_2^2}{2}, \frac{a_2^2+a_3^2}{2},...,\frac{a_{n-1}^2+a_n^2}{2}$ đều là các số chính phương.

 

file pdf [post='']http://www.mediafire...hc9zd1q6/ht.pdf[/post]

[shinichigl]

 

Câu 2: Cho dãy số $(x_n)$ được xác định bởi:

       $x_1=\frac{1}{2}; x_{n+1}=\frac{2014+x_n}{2016-x_n}$ với mọi $n=1,2,...$.

a. Chứng minh rằng dãy $(x_n)$ có giới hạn và tính giới hạn đó.

b. Với mỗi số tự nhiên $n \ge 1,$ đặt $y_n=\frac{1}{2013n+2015} \sum_{k=1}^{n} \frac{1}{x_k-2014}.$ Tính $\lim y_n$

 

a. Ta dễ dàng chứng minh bằng quy nạp $x_{n}\neq 1,\forall n=1,2,...$

$x_{n+1}-1=\frac{2\left ( x_{n}-1 \right )}{2016-x_{n}}$

$x_{n+1}-2014=\frac{2015\left ( x_{n}-2014 \right )}{2016-x_{n}}$

$\Rightarrow \frac{x_{n+1}-2014}{x_{n+1}-1}=\frac{2015}{2}\frac{x_{n}-2014}{x_{n}-1}=\left (\frac{2015}{2} \right )^{2}\frac{x_{n-1}-2014}{x_{n-1}-1}=...=\left (\frac{2015}{2} \right )^{n}\frac{x_{1}-2014}{x_{1}-1}=4027\left ( \frac{2015}{2} \right )^{n}$

$\Rightarrow x_{n+1}=\frac{2014.2^{n}-4027.2015^{n}}{2^{n}-4027.2015^{n}}$

$\Rightarrow \lim x_{n}=\lim \frac{2014.2^{n-1}-4027.2015^{n-1}}{2^{n-1}-4027.2015^{n-1}}=\lim \frac{2014.\left (\frac{2}{2015} \right )^{n-1}-4027}{\left (\frac{2}{2015} \right )^{n-1}-4027}=1$.

b. Từ công thức tìm được ở câu a) ta có

$\frac{1}{x_{n}-2014}=\frac{1}{2013.4027}\left [\left (\frac{2}{2015} \right )^{n-1}-4027 \right ]$

$\Rightarrow \sum_{k=1}^{n}\frac{1}{x_{k}-2014}=\frac{1}{2013.4027}\left [ 1+\frac{2}{2015}+\left ( \frac{2}{2015} \right )^{2}+...+\left ( \frac{2}{2015} \right )^{n-1} \right ]-\frac{n}{2013}=\frac{2015}{\left ( 2013 \right )^{2}.4027}\left [ 1-\left ( \frac{2}{2015} \right )^{n} \right ]-\frac{n}{2013}$

$\Rightarrow \lim y_{n}=\lim \left \{ \frac{2015}{\left ( 2013 \right )^{2}.4027}\left [ 1-\left ( \frac{2}{2015} \right )^{n} \right ]-\frac{n}{2013} \right \}\frac{1}{2013n+2015}=\lim \left \{ \frac{2015}{\left ( 2013 \right )^{2}.4027}\left [ 1-\left ( \frac{2}{2015} \right )^{n} \right ]\frac{1}{2013n+2015}-\frac{1}{2013^{2}+\frac{2013.2015}{n}} \right \}=-\frac{1}{2013^{2}}$.

Bài viết đã được chỉnh sửa nội dung bởi shinichigl: 09-09-2014 - 19:09

[Juliel]

 

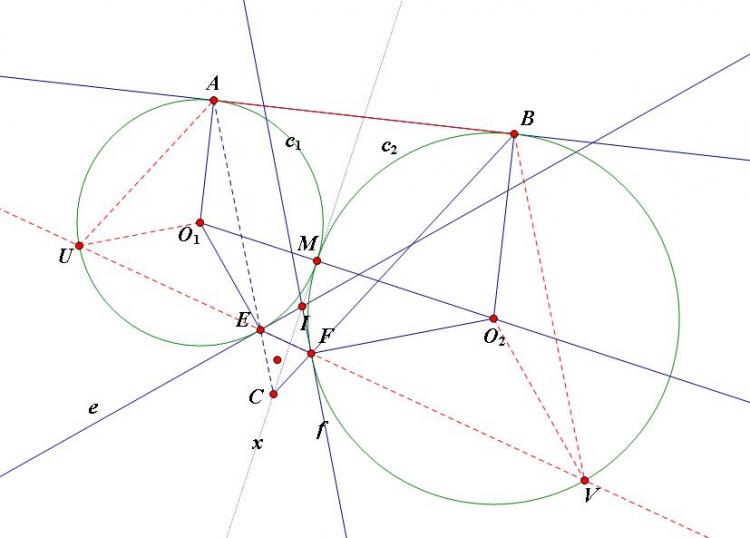
Câu 3: Cho 2 đường tròn $(C_1)$ và $(C_2)$ tiếp xúc ngoài nhau tại $M$. Tiếp tuyến chung ngoài $AB$, ($A$ thuộc $(C_1)$, $B$ thuộc $(C_2)$). Trên tia $Mx$ là tiếp tuyến chung của 2 đường tròn ( $Mx$ không cắt $AB$) lấy điểm $C$ khác $M$. Gọi $E,F$ lần lượt là giao điểm thứ 2 của $CA$ với $(C_1)$, $CB$ với $(C_2)$. Chứng minh rằng tiếp tuyến của $(C_1)$ tại $E$, tiếp tuyến của $(C_2)$ tại $F$ và $Mx$ đồng quy.

 

Lời giải :

 

Gọi $I$ là giao điểm của hai tiếp tuyến tại $E,F$ theo thứ tự của $(C_1),(C_2)$. Ta sẽ chứng minh tam giác $IEF$ cân tại $I$.

Cho $EF$ kéo dài cắt $(C_1),(C_2)$ theo thứ tự tại $U,V$.

Ta có :

$$\angle IEF=\angle UEe=\angle UAE=180^0-\left ( \angle AUE+\angle AEU \right )=180^0-\left ( \angle EAB+\angle AEU \right )\;\;\;(1)$$

$$\angle IFE=\angle VFf=\angle FBV=180^0-\left ( \angle BVF+\angle BFV \right )=180^0-\left ( \angle ABF+\angle BFV \right )\;\;\;(2)$$

Dễ thấy $Mx$ chính là trục đẳng phương của hai đường tròn mà $C\in Mx$ nên $C$ có cùng phương tích với hai đường tròn, tức là $CE.CA=CF.CB$, suy ra $E,F,A,B$ đồng viên. Ta được :

$$\angle EAB=\angle BFV,\angle AEU=\angle ABF\;\;\;(3)$$

Từ $(1)(2)(3)$ suy ra $\angle IEF=\angle IFE$, suy ra $IE=IF$. Kéo theo :

$$P_{I/(C_1)}=IE^2=IF^2=P_{I/(C_2)}$$

Tức $I$ thuộc $Mx$ là trục đẳng phương của $(C_1),(C_2)$. Điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi Juliel: 09-09-2014 - 22:01

[chardhdmovies]

 

KÌ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH GIỎI QUỐC GIA 12 THPT.

Thời gian: 180P, môn: Toán.

Câu 1: Giải hệ phương trình:

 $\left\{\begin{matrix} 3x^3+2x^2=y\\ 3y^3+2y^2=z\\ 3z^3+2z^2=x \end{matrix}\right.$

 

không mất tính tổng quát giả sử $x=max\left \{ x,y,z \right \}$

hệ tương đương $\left\{\begin{matrix} 3x^3+2x^2+x=x+y\\3y^3+2y^2+y=y+z \\3z^3+2z^2+z=z+x \end{matrix}\right.$

dễ thấy hàm $f(x)=3x^3+2x^2+x$ là hàm đồng biến nên $f(x)\geq f(z)\Rightarrow x+y\geq z+x\Rightarrow y\geq z\Rightarrow f(y)\geq f(z)\Rightarrow y+z\geq z+x\Rightarrow y\geq z$

do đó $x=y=z$

phần còn lại đơn giản rồi

 

NTP

[formath]

 

Câu 4: Cho số nguyên dương $n\ge 2.$ Chứng minh rằng $m=2n^2-1$ là số tự nhiên nhỏ nhất sao cho tồn tại $n$ số nguyên dương $a_1, a_2,...,a_n$ thỏa mãn đồng thời các điều kiện:

  i, $a_1<a_2<...<a_n=m$

  ii, Tất cả $n-1$ số $\frac{a_1^2+a_2^2}{2}, \frac{a_2^2+a_3^2}{2},...,\frac{a_{n-1}^2+a_n^2}{2}$ đều là các số chính phương.

 

Em xin được giải thế này ạ:
Cho $a$ là số nguyên dương cho trước. Một số $b >a$ thỏa mãn $\frac{a^{2}+b^{2}}{2}$ là số chính phương thì $b \geq \left \lfloor 2\sqrt{2a+2} \right \rfloor+2+a$
Thật vậy nếu đặt $b=a+d$ (d chẵn) thì $\frac{b^{2}+a^{2}}{2}=\frac{a^{2}+\left ( a+d \right )^{2}}{2}=a^{2}+ad+\frac{d^{2}}{2}$.
Mà $a^{2}+ad+\frac{d^{2}}{2} \geq (a+\frac{d}{2}+1)^{2} \Leftrightarrow d \geq \left \lfloor 2\sqrt{2a+2} \right \rfloor+2$
Ta có $a_1 \geq 1$
Giả sử $a_i \geq 2i^{2}-1$ với $i \geq 1$.
Dựa theo điều chứng minh ở trên ta có $a_{i+1} \geq \left \lfloor 2\sqrt{2a_i +2} \right \rfloor +a_i +2=2(i+1)^{2} - 1$
Do đó theo quy nạp ta có $a_n \geq 2n^{2}-1$
Suy ra $m \geq 2n^2 - 1$
Với $m = 2n^2 - 1$ ta chọn $a_i = 2i^{2} - 1$.
Từ đó có đpcm

Bài viết đã được chỉnh sửa nội dung bởi formath: 01-10-2014 - 21:06

[hoangtubatu955]

Lời giải đẹp quá!

Em xin được giải thế này ạ:
Cho $a$ là số nguyên dương cho trước. Một số $b >a$ thỏa mãn $\frac{a^{2}+b^{2}}{2}$ là số chính phương thì $b \geq \left \lfloor 2\sqrt{2a+2} \right \rfloor+2+a$
Thật vậy nếu đặt $b=a+d$ (d chẵn) thì $\frac{b^{2}+a^{2}}{2}=\frac{a^{2}+\left ( a+d \right )^{2}}{2}=a^{2}+ad+\frac{d^{2}}{2}$.
Mà $a^{2}+ad+\frac{d^{2}}{2} \geq (a+\frac{d}{2}+1)^{2} \Leftrightarrow d \geq \left \lfloor 2\sqrt{2a+2} \right \rfloor+2$
Ta có $a_1 \geq 1$
Giả sử $a_i \geq 2i^{2}-1$ với $i \geq 1$.
Dựa theo điều chứng minh ở trên ta có $a_{i+1} \geq \left \lfloor 2\sqrt{2a_i +2} \right \rfloor +a_i +2=2(i+1)^{2} - 1$
Do đó theo quy nạp ta có $a_n \geq 2n^{2}-1$
Suy ra $m \geq 2n^2 - 1$
Với $m = 2n^2 - 1$ ta chọn $a_i = 2i^{2} - 1$.
Từ đó có đpcm

[thukilop]

Bài tổ China 2013 : http://www.artofprob...247271#p3247271

[batdangthuc009]

cho mình hỏi bài dãy số câu 2a có thể sử dụng chuyển đẳng thức qua giới hạn để tìm lim được không?

[superpower]

 

KÌ THI CHỌN ĐỘI TUYỂN DỰ THI HỌC SINH GIỎI QUỐC GIA 12 THPT.

Thời gian: 180P, môn: Toán.

 

Câu 2: Cho dãy số $(x_n)$ được xác định bởi:

       $x_1=\frac{1}{2}; x_{n+1}=\frac{2014+x_n}{2016-x_n}$ với mọi $n=1,2,...$.

a. Chứng minh rằng dãy $(x_n)$ có giới hạn và tính giới hạn đó.

b. Với mỗi số tự nhiên $n \ge 1,$ đặt $y_n=\frac{1}{2013n+2015} \sum_{k=1}^{n} \frac{1}{x_k-2014}.$ Tính $\lim y_n$

 

 

câu dãy số 

Làm câu a cách chuyển sang giới hạn nhé

(*) ta chứng minh $x_n<=1$ với mọi n 

Thật vậy, ta có $x_1<=1$

Giả sử đúng với n=k, rồi dùng chứng minh tương đương là ra

Hơn thế nữa

 Khi ta xét hiệu $x_(n+1)-x_(n)$, kết hợp $x_n<=1$ với mọi n 

Suy ra {$x_n$} tăng, bị chặn trên 

Do đó tồn tại giới hạn, Đặt là L

chuyển sang giới hạn, ta có lim=1

[superfrankie98]

Em xin được giải thế này ạ:
Cho $a$ là số nguyên dương cho trước. Một số $b >a$ thỏa mãn $\frac{a^{2}+b^{2}}{2}$ là số chính phương thì $b \geq \left \lfloor 2\sqrt{2a+2} \right \rfloor+2+a$
Thật vậy nếu đặt $b=a+d$ (d chẵn) thì $\frac{b^{2}+a^{2}}{2}=\frac{a^{2}+\left ( a+d \right )^{2}}{2}=a^{2}+ad+\frac{d^{2}}{2}$.
Mà $a^{2}+ad+\frac{d^{2}}{2} \geq (a+\frac{d}{2}+1)^{2} \Leftrightarrow d \geq \left \lfloor 2\sqrt{2a+2} \right \rfloor+2$
Ta có $a_1 \geq 1$
Giả sử $a_i \geq 2i^{2}-1$ với $i \geq 1$.
Dựa theo điều chứng minh ở trên ta có $a_{i+1} \geq \left \lfloor 2\sqrt{2a_i +2} \right \rfloor +a_i +2=2(i+1)^{2} - 1$
Do đó theo quy nạp ta có $a_n \geq 2n^{2}-1$
Suy ra $m \geq 2n^2 - 1$
Với $m = 2n^2 - 1$ ta chọn $a_i = 2i^{2} - 1$.
Từ đó có đpcm

bạn giải thích kí hiệu này cho mình đc ko