Chủ đề này có 6 trả lời

[***lucky***]

cho phương trình http://dientuvietnam...cgi?x^{2}-2(a-1)x+2a-5=0
tìm giá trị của a để phương trình trên có hai nghiệm http://dientuvietnam...metex.cgi?x(x 1)(x+2)(x+3)=3

[ilovemoney_hic]

Ở bài 1 bạn hãy chuyển về phương trình ẩn (x-1) rồi tìm điều kiện để phương trình cod hai nghiệm trái dấu
Bài 2 bạn nhóm x(x+3) và (x+1)(x+2) lại rồi đạt ẩn phụ (http://dientuvietnam....cgi?x^{2} 3x 1)

Bài viết đã được chỉnh sửa nội dung bởi ilovemoney_hic: 19-04-2006 - 17:09

[ilovemoney_hic]

Đây em gợi ý thêm cho bác đây!
1) Ta có phương trình tương đương:

Phương trình ban đầu có nghiệm thỏa mãn ĐK khi pt trên có 2 nghiệm trái dấu()
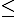
0 và P <0
2)ĐẶt ẩn phụ như thế thì ra phương trình bậc hai còn gì?!?

[Lebnit]

Bai 1 co the giai theo cach lop 10 ,chi can tinh dieu kien de

[ilovemoney_hic]

Vâng!Em nghe nói với kiến thức cấp 3 có thể so sánh các nghiệm của một phương trình với một số bất kì (nhưng với cấp hai thì chỉ có thể làm như trên). Nếu không phiền bác có thể giới thiệu cách đó cho em được không ạ ???

[Prudential112410]

Vâng!Em nghe nói với kiến thức cấp 3 có thể so sánh các nghiệm của một phương trình với một số bất kì (nhưng với cấp hai thì chỉ có thể làm như trên). Nếu không phiền bác có thể giới thiệu cách đó cho em được không ạ ???

À! Có thể so sánh nghiệm với 2 số nữa
Để khi nào rãnh anh post cho.
Nếu muốn tìm hiểu thì chỉ việc mua SGK Đại số 10
Bye!

[***lucky***]

cách anh lebnit đưa ra có phải là thế này không ạ:
để x_{1} <n< x_{2} thì ta chỉ cần tìm điều kiện sao cho af(n) 0 không ạ

Bài viết đã được chỉnh sửa nội dung bởi ***lucky***: 06-05-2006 - 15:54