Mình nghĩ thi HSG 9 thì bài này là căn nguyên của hầu hết các bài về đường tròn
Bài 35: (Đề thi HSG cấp tỉnh lớp 9 tỉnh Vĩnh Phúc 2010) (MOSP 1995)
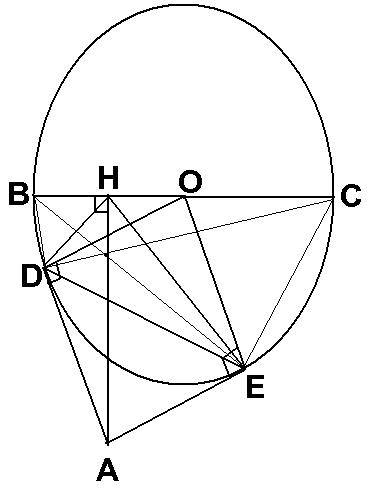
Cho tam giác nhọn $ABC$ nội tiếp $(O)$. $AD,BE,CF$ là các đường cao. Đường thẳng $EF$ cắt $BC$ tại $G$, đường thẳng $AG$ cắt đường tròn tại điểm $M$
1) Chứng minh rằng bốn điểm $A,M,E,F$ cùng nằm trên đường tròn
2) Gọi $N$ là trung điểm của cạnh $BC$ và $H$ là trược tâm tam giác $ABC$. Chứng minh rằng: $GH$ vuông góc $AN$
a,Ta có tứ giác BFEC nội tiếp,G là giao điểm EF và BC
$\Rightarrow$ GE.GF=GB.GC
Tứ giác AMBC nội tiếp,G là giao điểm AM và BC
$\Rightarrow$ GM.GA=GB.GC
$\Rightarrow$ GM.GA=GE.GF
$\Rightarrow$ Tứ giác AMFE nội tiếp.
b,Dễ ch/m được M thuộc đường tròn đường kính AH do đó,HM vuông góc MA
Kẻ MH cắt (O) tại K $\rightarrow $AK là đường kính của $(O)$
suy ra KC//BH(cùng vuông góc với $AC$)
KB//CH(cùng vuông góc với $AB$)
$\Rightarrow$ BHCK là hình bình hành
$\Rightarrow$ HK đi qua N
$\Rightarrow$ H,M,N thẳng hàng
Tam giác GAN có 2 đường cao AD,MN cắt nhau tại H nên H là trực tâm $\Delta GAN $
$\Rightarrow$ GH vuông góc với AN $(Q.E.D)$