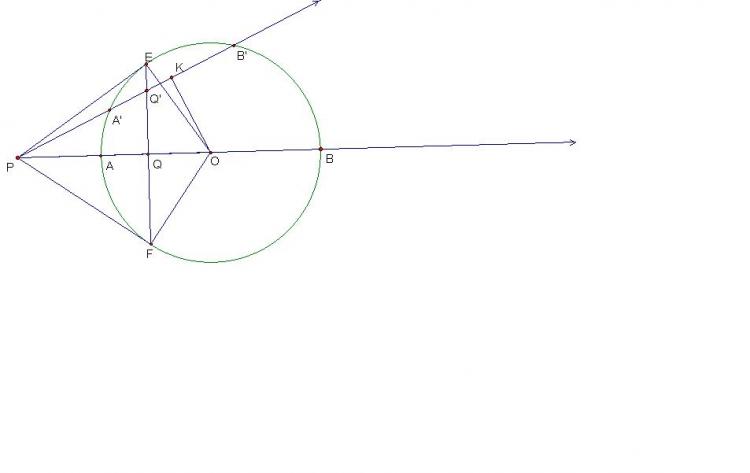
a) Khi cát tuyến đi qua $O$, Chứng minh : $\dfrac{PA}{PB} = \dfrac{QA}{QB} \textbf{ (1)}$
b) Đẳng thức $(1)$ có còn đúng không, khi cát tuyến trên không đi qua điểm $O$?
Hãy chứng minh điều đó.
Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 03-03-2013 - 00:19