[Trường Xuân toán miền Nam]Vietnam TST 2016 Mock Test 1
#1
 Đã gửi 24-02-2016 - 12:39
Đã gửi 24-02-2016 - 12:39

- anhtukhon1, canhhoang30011999, Tran Nguyen Lan 1107 và 8 người khác yêu thích
Discovery is a child’s privilege. I mean the small child, the child who is not afraid to be wrong, to look silly, to not be serious, and to act differently from everyone else. He is also not afraid that the things he is interested in are in bad taste or turn out to be different from his expectations, from what they should be, or rather he is not afraid of what they actually are. He ignores the silent and flawless consensus that is part of the air we breathe – the consensus of all the people who are, or are reputed to be, reasonable.
Grothendieck, Récoltes et Semailles (“Crops and Seeds”).
#2
 Đã gửi 24-02-2016 - 17:42
Đã gửi 24-02-2016 - 17:42

Lời giải bài hình:
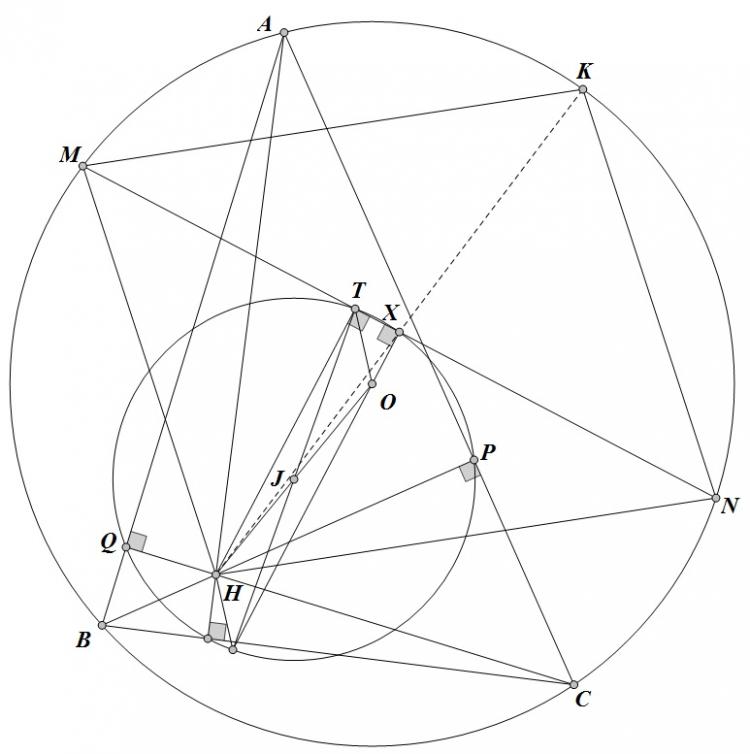
Câu a) Gọi $X$ là giao của $MN$ với với $T$. Do $J$ là tâm đường tròn $Euler$ nên $J$ là trung điểm $OH$. $T'$ đối xứng với $T$ qua $J$ thì $HOTT'$ là hình bình hành $\Rightarrow T'O//HT \Rightarrow T'O$ vuông góc với $MN$ hay $T',O,X$ thẳng hàng. Vậy $X$ là trung điểm $MN$.
$\Rightarrow K$ thuộc $HX$. Mặt khác theo tính chất của đường tròn $Euler$, kết hợp với $XH=XK$ thì $K$ thuộc $(O)$.
Vậy $K$ luôn chạy trên một đường cố định.
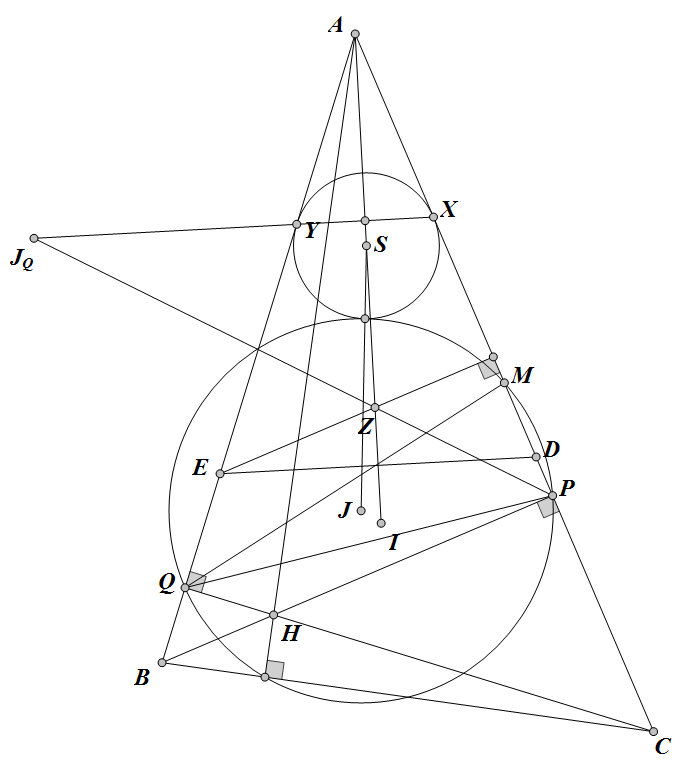
Câu b)Gọi $M$ là trung điểm $AC$. $P,Q$ là chân đường cao hạ từ $B,C$ xuống $AC,AB$.
Áp dụng bổ đề $Sayawama$ mở rộng cho tâm bàng tiếp với $\triangle PMQ$ thì $XY$ đi qua tâm bàng tiếp $\angle P$.
$R$ là hình chiếu của $E$ lên $AB$. Dễ thấy $\triangle PRZ\sim \triangle BEI$ nên $Z$ thuộc phân giác $\angle MPQ$.
Gọi $J_{P}$ là tâm bàng tiếp $\angle P$ thì $J_{Q},Z,P$ thẳng hàng.
$AYXZ$ là hình thoi khi và chỉ khi $\triangle J_{Q}AZ$ cân. Ta có biến đổi góc: $\angle AZJ_{Q}=90^{\circ}-\angle C/2$
Vậy ta chỉ cần chứng minh $\angle AJ_{Q}P=\angle C$. Gọi $S$ là chân đường phân giác kẻ từ $B$ xuống $AC$. Dễ thấy $\triangle BSC\sim \triangle AJ_{Q}P(c.g.c)$
Vậy ta có điều phải chứng minh!
Bài viết đã được chỉnh sửa nội dung bởi baopbc: 24-02-2016 - 18:10
- perfectstrong, Zaraki, canhhoang30011999 và 9 người khác yêu thích
#3
 Đã gửi 24-02-2016 - 19:09
Đã gửi 24-02-2016 - 19:09

Trường Xuân toán học miền Nam 2016Vietnam TST 2016 MOCK Test 1Ngày thi: 24/2/2016Thời gian làm bài: 240 phútBài 1.Cho a, b, c là các số thực dương. Chứng minh rằng ta có bất đẳng thức$$\frac{ab+bc+ca+\sqrt{a^2b^2+b^2c^2+c^2a^2}}{a+b+c+\sqrt{a^2+b^2+c^2}} \le \frac{a+b+c}{3}$$
Mình xin làm bài bất đẳng thức
Đặt $a+b+c=p , ab+bc+ca=q , abc=r $
Ta cần chứng minh bđt
$\frac{q+\sqrt{q^2-2pr}}{p+\sqrt{p^2-2q}} \geq \frac{p}{3} $
Bằng cách bình phương 2 vế, ta đưa được về dạng $f(r) \geq 0$
Mà ta có $f'(r) \geq 0 $ nên theo định lý $PQR$, ta chỉ cần chứng minh bđt trong trường hợp có $2$ số bằng nhau
Không mất tính tổng quát, giả sử $a=b $
Chuẩn hóa $abc=1 => c=\frac{1}{a^2} $
BĐT trở thành
$f(a)=a^2-\frac{2}{a} +\frac{1}{a^4} + 2\sqrt{2a^4+1} +\sqrt{\frac{2}{a^2}+ \frac{1}{a^6}}-3\sqrt{a^4+\frac{2}{a^2}} \geq 0 $
Khảo sát hàm 1 biến, ta thấy $f(a) \geq f(1) = 0$
Do đó, ta có điều phải chứng minh
Dấu bằng xảy ra khi $a=b=c $
Cách này hơi trâu
Mong chờ một lời giải đẹp từ các bạn
- Zaraki, canhhoang30011999, HoangVienDuy và 2 người khác yêu thích
#4
 Đã gửi 24-02-2016 - 20:01
Đã gửi 24-02-2016 - 20:01

Mình xin làm bài bất đẳng thức
Đặt $a+b+c=p , ab+bc+ca=q , abc=r $
Ta cần chứng minh bđt
$\frac{q+\sqrt{q^2-2pr}}{p+\sqrt{p^2-2q}} \geq \frac{p}{3} $
Bằng cách bình phương 2 vế, ta đưa được về dạng $f(r) \geq 0$
Mà ta có $f'(r) \geq 0 $ nên theo định lý $PQR$, ta chỉ cần chứng minh bđt trong trường hợp có $2$ số bằng nhau
Không mất tính tổng quát, giả sử $a=b $
Chuẩn hóa $abc=1 => c=\frac{1}{a^2} $
BĐT trở thành
$f(a)=a^2-\frac{2}{a} +\frac{1}{a^4} + 2\sqrt{2a^4+1} +\sqrt{\frac{2}{a^2}+ \frac{1}{a^6}}-3\sqrt{a^4+\frac{2}{a^2}} \geq 0 $
Khảo sát hàm 1 biến, ta thấy $f(a) \geq f(1) = 0$
Do đó, ta có điều phải chứng minh
Dấu bằng xảy ra khi $a=b=c $
Cách này hơi trâu
Mong chờ một lời giải đẹp từ các bạn
Bài này cho đơn giản thì chuẩn hóa $p=3$ sau đó dùng bất đẳng thức Schur $r\geq \dfrac{4q-9}{3}$ sẽ đơn giản hơn nhiều
Ta có bất đẳng thức tương đương $\dfrac{q+\sqrt{q^2-2pr}}{p+\sqrt{p^2-2q}}\leq \dfrac{p}{3}$
Chuẩn hóa $p=3$ thì cần chứng minh $q+\sqrt{q^2-6r}\leq 3+\sqrt{9-2q}$
Áp dụng bất đẳng thức Schur thì $r\geq \dfrac{4q-9}{3}$, ta cần chứng minh $q+\sqrt{q^2-8q+18}\leq 3+\sqrt{9-2q}$
Đây là bất đẳng thức một biến, xét đạo hàm sẽ ra. Hoặc biến đổi tương đương cho đỡ ( chúa ghét đạo hàm chứa căn ![]() )
)
Bất đẳng thức cần chứng minh tương đương với $(3-q).\left (1-\dfrac{3-q}{\sqrt{q^2-8q+18}+\sqrt{9-2q}}\right )\geq 0$
Luôn đúng do $3\geq q$ và $\sqrt{q^2-8q+18}>\sqrt{q^2-6q+9}\geq 3-q$
Dấu "=" khi $a=b=c$
Bài viết đã được chỉnh sửa nội dung bởi hoanglong2k: 24-02-2016 - 20:10
- Zaraki, canhhoang30011999, huuhieuht và 4 người khác yêu thích
#5
 Đã gửi 25-02-2016 - 01:23
Đã gửi 25-02-2016 - 01:23

Bài 3.
a) Chọn CSC $5, 17, 29, \cdots$.
Khi đó $\left(\frac{-1}{5}\right) = \left(\frac{-1}{17}\right) = \left(\frac{-1}{29}\right) = 1$. Nghĩa là tồn tại $a, b, c$ sao cho với $x \equiv a \pmod{5}$ thì $x^{2} + 1 \vdots 5$ (tương tự cho $17, 29$). Ta có hệ đồng dư:
$$\begin{cases} n\equiv a\pmod{5} \\ n\equiv b\pmod{17} \\ n\equiv c\pmod{29}\end{cases}$$
Do $(5; 17) = (17;29) = (29; 5) = 1$ nên theo định lý thặng dư Trung Hoa tồn tại $n$ để $n^{2} + 1 \vdots 5\times 17\times 29$
b) Gọi 3 số hạng luôn có mặt của dãy là $a, b, c$
Bổ đề 1. Mọi số nguyên dạng $4k + 3$ luôn có ước nguyên tố dạng $4n + 3$.
Bổ đề 2. Khồng tồn tại $p\in \mathbb{P}$ dạng $4k + 3$ sao cho $p\mid n^{2} + 1$ với $n$ tự nhiên nào đó.
TH1. $d = 10$. Giả sử tồn tại thoả có bộ chuẩn với $d = 10$. Nếu $a \equiv 0\pmod{2}$ thì $b, c$ cũng vậy. Do đó $4\mid abc$. Mặt khác, $n^{2} + 1 \equiv 1 \text{hoặc} 2\pmod{4}$. Do đó $abc\nmid n^{2} + 1$.
Nếu $a$ lẻ thì toàn bộ số hạng đều lẻ. Nếu $a \equiv 1\pmod{4}$ thì $b\equiv 3\pmod{4}$. Theo bổ đề 1 tồn tại số nguyên tố dạng $4k + 3$. Do đó $(4k + 2)\mid n^{2} + 1$, vô lí. Nếu $a\equiv 3\pmod{4}$ thì tương tự cũng có điều vô lí.
TH2. $d = 11$. Cũng giả sử ngược lại. Nếu $a \equiv 0\pmod{4}$ thì $4\mid abc$ và ta cũng có điều vô lí. Nếu $a \equiv 2\pmod{4}$ thì $c\equiv 0\pmod{4}$, dẫn đến $4\mid 8\mid abc$, vô lí. Nếu $a \equiv 3\pmod{4}$ thì cũng vô lí. Nếu $a\equiv 1\pmod{4}$ thì $c \equiv 3\pmod{4}$ cũng dẫn đến điều vô lí.
Tóm lại không có bộ chuẩn công sai $10$ hay $11$ (nói chung là không có bộ chuẩn công sai dạng $4k + 2$ hay $4k + 3$).
Đây là lời giải mình gõ đàng hoàng bên mathscope.
P.s: hôm nay mình thi ở trường, vô phòng thi cũng chán làm ra nốt câu c), cũng giống như Zaraki làm :-)
Bài viết đã được chỉnh sửa nội dung bởi Ego: 25-02-2016 - 11:11
- Zaraki, canhhoang30011999, CaptainCuong và 3 người khác yêu thích
#6
 Đã gửi 25-02-2016 - 05:05
Đã gửi 25-02-2016 - 05:05

Xin xử lí luôn câu c. ![]()
Ta có một bổ đề khác sau:
Bổ đề 3. Với mỗi số nguyên tố $p\equiv 1 \pmod{4}$ thì luôn tồn tại số nguyên dương $k$ thoả $p \mid k^2+1$.
Chứng minh thì ta thấy $-1$ là số chính phương mod $p$ nên luôn tồn tại $k$.
Nếu cấp số cộng có nhiều hơn $6$ số hạng thì tồn tại một số hạng chia hết cho $7$. Để ý rằng $7 \equiv 3 \pmod{4}$ nên bổ đề 1 suy ra điều mâu thuẫn.
Vậy cấp số cộng có nhiều nhất $6$ số hạng. Ta chứng minh tồn tại cấp số cộng có $6$ số hạng như thế bằng cách chỉ ra cấp số cộng $5,17,29,41, 53, 65$ thoả mãn qua bổ đề 3 và Định lý Thặng dư Trung hoa. Thật vậy, với mỗi ước nguyên tố $p_i$ của các số hạng trong cấp số cộng trên, luôn tồn tại $k_i$ thoả $p_i \mid k_i^2+1$ (riêng với $p=5$ do thì $k=7$ để có được $25 \mid k^2+1$) do đó luôn tồn tại $n$ theo Định lý Thặng dư Trung hoa thoả mãn $n \equiv k_i \pmod{p_i}$. Khi đó $5 \cdot 17 \cdot 29 \cdot 41 \cdot 53 \cdot 65 \mid n^2+1$.
Vậy $6$ là câu trả lời cho bài toán.
Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 25-02-2016 - 05:08
- canhhoang30011999, baopbc, NTA1907 và 2 người khác yêu thích
Discovery is a child’s privilege. I mean the small child, the child who is not afraid to be wrong, to look silly, to not be serious, and to act differently from everyone else. He is also not afraid that the things he is interested in are in bad taste or turn out to be different from his expectations, from what they should be, or rather he is not afraid of what they actually are. He ignores the silent and flawless consensus that is part of the air we breathe – the consensus of all the people who are, or are reputed to be, reasonable.
Grothendieck, Récoltes et Semailles (“Crops and Seeds”).
#7
 Đã gửi 25-02-2016 - 12:19
Đã gửi 25-02-2016 - 12:19

Sẵn tiện rảnh mình sẽ post lời giải của mình. Có hai hướng đi và mình sẽ cung cấp một bổ đề mình nghĩ là mạnh hơn. Thật ra bài của bạn Zaraki việc chọn $k = 7$ là đẹp rồi.
Hướng 1. (mình vô tình vừa nghĩ được).
Với $7$ số thì tương tự như bạn Zaraki. Với $6$ số. Ta chọn 6 số cấp số cộng sao cho ước nguyên tố của chúng đều có dạng $4k + 1$ (rất nhiều cách chọn, có thể chọn ra cụ thể), gọi tích của chúng là $P$. Sử dụng đẳng thức $(a^{2} + b^{2})(c^{2} + d^{2}) = (ac + bd)^{2} + (ad - bc)^{2}$ ta có được tích của chúng dạng $u^{2} + v^{2}$. Chọn $u, v$ sao cho $\text{gcd}(u, v) = 1$. Khi đó xét $n' = (ur)^{2} + (vr)^{2} \vdots P$. Chọn $r$ sao cho $vr \equiv 1 \pmod{P}$. Do $\text{gcd}(u, v) = 1$ nên $\text{gcd}(v, P) = 1$. Do đó ta chọn được $r$. Khi đó chọn $n^{2} + 1$ sao cho $n \equiv ur \pmod{P}$. Từ đó có $n^{2} + 1 \equiv (ur)^{2} + (vr)^{2} \equiv 0 \pmod{P}$.
Hướng 2.
Bổ đề. Cho $p$ là số nguyên tố lẻ sao cho $\left(\frac{-1}{p}\right) = 1$. Khi đó luôn tồn tại $n$ để $p^{t} \mid n^{2} + 1$.
Chứng minh. Dĩ nhiên là tồn tại $n^{2} + 1 \vdots p$. Giả sử có tồn tại $v_{p}(n^{2} + 1) = t$, giả sử $n^{2} + 1 = p^{t}.r$ với $\text{gcd}(r, p) = 1$. Đặt $m = n + p^{t}.K$. Khi đó $m^{2} + 1 = n^{2} + 1 + 2np^{t}.K + p^{2t}.K^{2} \equiv r.p^{t} + 2nK.p^{t} = p^{t}(r + 2nK) \pmod{p^{t + 1}}$. Chọn $K$ sao cho $r + 2nK \vdots p$. Vậy bổ đề đúng theo quy nạp.
Dùng bổ đề ta có được điều phải chứng minh :-).
p.s: Hôm qua định dùng bổ đề này chứng minh cho 2 câu kia mà thấy hơi quá tay =))
Bài viết đã được chỉnh sửa nội dung bởi Ego: 25-02-2016 - 12:21
- Zaraki, phamhuy1801, baopbc và 1 người khác yêu thích
#8
 Đã gửi 25-02-2016 - 20:30
Đã gửi 25-02-2016 - 20:30

Lời giải bài hình:
Câu a) Gọi $X$ là giao của $MN$ với với $T$. Do $J$ là tâm đường tròn $Euler$ nên $J$ là trung điểm $OH$. $T'$ đối xứng với $T$ qua $J$ thì $HOTT'$ là hình bình hành $\Rightarrow T'O//HT \Rightarrow T'O$ vuông góc với $MN$ hay $T',O,X$ thẳng hàng. Vậy $X$ là trung điểm $MN$.
$\Rightarrow K$ thuộc $HX$. Mặt khác theo tính chất của đường tròn $Euler$, kết hợp với $XH=XK$ thì $K$ thuộc $(O)$.
Vậy $K$ luôn chạy trên một đường cố định.
Câu b)Gọi $M$ là trung điểm $AC$. $P,Q$ là chân đường cao hạ từ $B,C$ xuống $AC,AB$.
Áp dụng bổ đề $Sayawama$ mở rộng cho tâm bàng tiếp với $\triangle PMQ$ thì $XY$ đi qua tâm bàng tiếp $\angle P$.
$R$ là hình chiếu của $E$ lên $AB$. Dễ thấy $\triangle PRZ\sim \triangle BEI$ nên $Z$ thuộc phân giác $\angle MPQ$.
Gọi $J_{P}$ là tâm bàng tiếp $\angle P$ thì $J_{Q},Z,P$ thẳng hàng.
$AYXZ$ là hình thoi khi và chỉ khi $\triangle J_{Q}AZ$ cân. Ta có biến đổi góc: $\angle AZJ_{Q}=90^{\circ}-\angle C/2$
Vậy ta chỉ cần chứng minh $\angle AJ_{Q}P=\angle C$. Gọi $S$ là chân đường phân giác kẻ từ $B$ xuống $AC$. Dễ thấy $\triangle BSC\sim \triangle AJ_{Q}P(c.g.c)$
Vậy ta có điều phải chứng minh!
đoạn cuối bảo nói rõ luôn đi
- Tran Nguyen Lan 1107 và baopbc thích
#9
 Đã gửi 25-02-2016 - 21:13
Đã gửi 25-02-2016 - 21:13

Chỗ đó em giải hơi rườm, thực ra nó là bài toán sau:
Cho tam giác $ABC$. $E,F$ lần lượt là hình chiếu từ $B,C$ xuống $AC,AB$. $M$ là trung điểm $AC$. $J_{E}$ là tâm bàng tiếp góc $E$. Chứng minh rằng: $\angle AJ_{E}P=\angle C$
Chứng minh: Điều này tương đương với chứng minh: $AEFJ_{E}$ là tứ giác nội tiếp
Ta có biến đổi góc: $\angle FJ_{E}E=\angle EMF/2=\angle A$ (đẳng thức cuối đúng do $FM$ là trung tuyến ứng với cạnh huyền trong tam giác vuông)
Bài viết đã được chỉnh sửa nội dung bởi baopbc: 26-02-2016 - 16:11
- canhhoang30011999, Tran Nguyen Lan 1107 và NHoang1608 thích
#10
 Đã gửi 26-02-2016 - 03:02
Đã gửi 26-02-2016 - 03:02

Ta chọn 6 số cấp số cộng sao cho ước nguyên tố của chúng đều có dạng $4k + 1$ (rất nhiều cách chọn, có thể chọn ra cụ thể),
Ego có thể giới thiệu thêm một số cách chọn khác ngoài việc chọn cụ thể được không ? ![]()
Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 26-02-2016 - 03:06
Discovery is a child’s privilege. I mean the small child, the child who is not afraid to be wrong, to look silly, to not be serious, and to act differently from everyone else. He is also not afraid that the things he is interested in are in bad taste or turn out to be different from his expectations, from what they should be, or rather he is not afraid of what they actually are. He ignores the silent and flawless consensus that is part of the air we breathe – the consensus of all the people who are, or are reputed to be, reasonable.
Grothendieck, Récoltes et Semailles (“Crops and Seeds”).
#11
 Đã gửi 07-04-2017 - 00:18
Đã gửi 07-04-2017 - 00:18

myfb : www.facebook.com/votiendung.0805
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~o0o~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
SỢ HÃI giúp ta tồn tại
NGHỊ LỰC giúp ta đứng vững
KHÁT VỌNG giúp ta tiến về phía trước
Võ Tiến Dũng
![]()
![]()
![]()
![]()
![]()
Được gắn nhãn với một hoặc nhiều trong số những từ khóa sau: tst, mock, trường xuân toán học
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh