Chủ đề này có 34 trả lời

[Zaraki]

VN TST 2016

Thời gian thi: 4 tiếng 30 phút

Ngày 1

 

Bài 1. Tìm $a,n$ nguyên dương với $a>2$ để mỗi ước nguyên tố của $a^n-1$ cũng là ước nguyên tố của $a^{3^{2016}}-1.$

 

Bài 2. $A$ là tập $2000$ số nguyên phân biệt và $B$ là tập $2016$ số nguyên phân biệt. $K $ là số cặp $(m,n)$ có thứ tự với $m$ thuộc $A$ và $n$ thuộc $B$ mà $|m-n|\leq 1000$. Tìm max $K$?

 

Bài 3. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ có $B,C$ cố định, $A$ chuyển động trên cung $BC$ của $ (O)$. Các phân giác $AD,BE,CF$ giao nhau tại $I$. Đường tròn qua $D$ tiếp xúc với $OA$ tại $A$ cắt $(O)$ tại $G$. $GE,GF$ giao $(O)$ lần thứ hai tại $M,N$. $BM$ giao $CN$ tại $H.$

a) Chứng minh rằng $AH$ đi qua một điểm cố định.

b) $BE, CF$ giao $(O)$ lần lượt tại $K,L$. $AH$ giao $KL$ tại $P$. $Q$ là một điểm trên $EF$ sao cho $QP=QI.$ $J$ là điểm nằm trên $(BIC)$ sao cho $IJ\perp IQ$. Chứng minh rằng trung điểm $IJ$ chuyển động trên một đường tròn cố định.

 

Ngày 2.

 

Bài 4. Cho tam giác $ABC$ nhọn có $\angle ACB<\angle ABC<\angle ACB+ \dfrac{\angle BAC}{2}$. Lấy điểm $D$ thuộc cạnh $BC$ sao cho $\angle ADC=\angle ACB+\dfrac{\angle BAC}{2}$. Tiếp tuyến với đường tròn ngoại tiếp tam giác $ABC$ tại $A$ cắt $BC$ tại $E$. Phân giác $\angle AEB$ cắt $AD$ và cắt $(ADE)$ tại $G$ và $ F$, $DF$ giao $AE$ tại $H.$

a) Chứng minh rằng các đường tròn đường kính $AE,DF,GH$ có một điểm chung.

b) Trên phân giác ngoài $\angle BAC $ và trên tia $AC$ lần lượt lấy các điểm $K$ và $M$ sao cho $KB=KD=KM$, trên phân giác ngoài $\angle BAC$ và trên tia $AB$ lần lượt lấy các điểm $L$ và $N$ sao cho $LC=LD=LN.$ Đường tròn đi qua $M,N$ và trung điểm $I$ của $BC$ cắt $BC$ tại $P$ ($P\neq I$). Chứng minh rằng $BM,CN,AP$ đồng quy.

 

Bài 5. Cho $a_1,a_2,...,a_{n-1},a_n$ ($n\geq 3$), trong đó mỗi số $a_i $ nhận giá trị $\in \{0;1\}$. Xét $n$ bộ số $S_1=(a_1,a_2,...,a_{n-1},a_n)$, $S_2=(a_2,a_3,...,a_n,a_1)$;...;$S_n=(a_n, a_1, ..., a_{n-2},a_{n-1})$.  Với mỗi bộ số $r=(b_1,b_2,...,b_n)$, đặt $\omega(r)=b_1.2^{n-1}+b_2.2^{n-2}+...+b_n.2^0.$ Giả sử các số $\omega(S_1); \omega(S_2);...;\omega(S_n)$ nhận đúng $k $ giá trị phân biệt.

a) Chứng minh rằng $k \mid n$ và $ \dfrac{2^n-1}{2^k-1} \mid \omega(S_i)$  $\forall i=\overline{1,n}.$

b) Kí hiệu $M$ và $m$ lần lượt là max và min của $\omega(S_1),...,\omega(S_n)$. Chứng minh rằng $M-m\geq \dfrac{(2^n-1)(2^{k-1}-1)}{2^k-1}.$

 

Bài 6. Cho các số thực phân biệt $\alpha_1,\alpha_2,...,\alpha_{16}$. Với mỗi đa thức hệ số thực $P(x)$; đặt $V(P)=P(\alpha_1)+P(\alpha_2)+...+P(\alpha_{16}).$

Chứng minh rằng tồn tại duy nhất đa thức $Q(x)$ bậc 8 có hệ số $x^8$ bằng $1$ thỏa mãn

i) $V(Q(x) \cdot P(x))=0$ với mọi đa thức $P$ có bậc bé hơn $8.$

ii) $Q(x)$ có $8$ nghiệm thực (tính cả bội).

 

Nguồn: MathScope.

Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 28-03-2016 - 18:26
Thêm Ngày 2

[quanghung86]

Bài hình ý b) nên viết lại như sau cho đẹp

 

Bài toán. Cho tam giác $ABC$ với phân giác $BE,CF$ cắt nhau tại $I$, tâm ngoại tiếp $O$. Đường thẳng qua $I$ vuông góc $OI$ cắt $BC,EF$ tại $M,N$. Chứng minh rằng $IM=2IN$.

 

Giải. Gọi $BE,CF$ cắt $(O)$ tại $P,Q$ khác $B,C$. $EF$ cắt $BC$ tại $X$. $AI$ cắt $BC,EF$ tại $Y,Z$. $MN$ cắt $PQ,AS$ tại $K,L$. Theo bài toán con bướm dễ thấy $IM=IK$. Mặt khác dễ thấy $PQ$ là trung trực $AI$. $AX$ là phân giác ngoài góc $A$ nên $IL=2IK=2IM$ hay $ML=3MI$. Lại có hàng điều hòa cơ bản $(AI,YZ)=-1$ nên $X(AI,YZ)=-1$ chiếu chùm này lên đường thẳng $MN$ thì hàng $(LI,MN)=-1$, từ đó $\frac{NL}{NI}=\frac{ML}{MI}=3$ hay $IN=\frac{1}{4}IL=\frac{1}{2}IM$. Ta hoàn thành chứng minh.

 

Theo mình ý tưởng của ý b) hay và mới, tuy nhiên cũng khá mẹo mực!

Hình gửi kèm

• 

[Zaraki]

Bài 1 nếu ai biết đến bổ đề $\gcd \left( a^m-1,a^n-1 \right) = a^{ \gcd (m,n)}-1$ thì sẽ xử lí rất nhanh gọn.

[Chris yang]

Bài 1 có được hiểu là $a^n-1$ và $a^{3^{2016}}-1$ có cùng tập ước nguyên tố không nhỉ? Mình không chắc chắn nhưng nếu là vậy thì định lý Zsigmondy có thể giải quyết nó.

[Zaraki]

Bài 1 có được hiểu là $a^n-1$ và $a^{3^{2016}}-1$ có cùng tập ước nguyên tố không nhỉ? Mình không chắc chắn nhưng nếu là vậy thì định lý Zsigmondy có thể giải quyết nó.

Mình không nghĩ ta có thể hiểu như thế, vì họ nói mọi ước nguyên tố của $a^n-1$ đều là ước nguyên tố của $a^{3^{2016}}-1$ nhưng chưa chắc mọi ước nguyên tố của $a^{3^{2016}}-1$ là ước nguyên tố của $a^n-1$.

[Ego]

Như Zaraki nói, ta sẽ sử dụng bổ đề $\text{gcd}(a^{m} - 1, a^{n} - 1) = a^{\text{gcd}(m, n)} - 1$
Bổ đề 1. $\text{gcd}(a^{m} - 1, a^{n} - 1) = a^{\text{gcd}(m, n)} - 1$
Chứng minh bổ đề. Gọi $d = \text{gcd}(a^{m} - 1, a^{n} - 1)$
Để ý $a^{\text{gcd}(m, n)} - 1 \mid a^{m} - 1, a^{n} - 1 \implies a^{\text{gcd}(m, n)} - 1 \mid d \implies d \ge a^{\text{gcd}(m, n)} - 1$
Mặt khác $a^{m} \equiv 1 \pmod{d}$ và $a^{n} \equiv 1\pmod{p}$ nên $\text{ord}_{d}(a) \mid m, n \implies \text{ord}_{d}(a) \mid \text{gcd}(m, n)$
Hay $a^{\text{gcd}(m, n)} \equiv 1 \pmod{d}$ hay $a^{\text{gcd}(m, n)} - 1 \ge d$.
Kết hợp lại ta có đpcm.
Bổ đề 2. $3^{3^{u}} + 1 = 2^{t}$ có nghiệm duy nhất là $(u, t) = (0, 2)$.
Chứng minh bổ đề. Xét $u \ge 1$, khi đó $3^{3^{u}} = (3^{3})^{3^{u - 1}} \equiv 3^{3^{u - 1}}\pmod{8}$. Đến đây lùi về sẽ thu được $3^{3^{u}} \equiv 3\pmod{8}$. Từ đó ta có $u = 0$ là nghiệm duy nhất.

Giả thiết bài toán quy thành $p$ là ước nguyên tố của $a^{n} - 1$ thì $p\mid d$ với $d = \text{gcd}(a^{n} - 1, a^{3^{2016}} - 1)$
Ta đặt $n = 3^{u}.v$ với $\text{gcd}(v, 3) = 1$.

• TH1. $u \le 2016$. Khi đó theo bổ đề $d = a^{3^{u}} - 1$
  i) Nếu $v = 1$ thì ta dễ thấy $a^{3^{u}} - 1 \mid a^{3^{2016}} - 1$.
  ii) Xét $v \ge 2$, khi đó ta có $a^{v} - 1\mid a^{n} - 1$. Bài toán suy ra nếu $p\mid a^{v} - 1$ thì $p\mid a^{3^{u}} - 1$. Xét $p$ là ước nguyên tố của $\frac{a^{v} - 1}{a - 1} \implies p\mid a^{v} - 1$. Khi đó $p\mid \text{gcd}(a^{v} - 1, a^{3^{u}} - 1) = a - 1$ theo bổ đề trên. Điều này có nghĩa là tập các ước nguyên tố của $a^{v - 1} + a^{v - 2} + \cdots + 1$ phải là tập con của tập các ước nguyên tố của $a - 1$ (*)
  Bây giờ ta đặt $A = a^{v - 1} + a^{v - 2} + \cdots + 1 = p_{1}^{d_{1}}p_{2}^{d_{2}}\cdots p_{k}^{d_{k}}$ với $p_{i} < p_{i + 1}$ là các ước nguyên tố.
  Theo (*) thì $a - 1 = p_{1}^{c_{1}}p_{2}^{c_{2}}\cdots p_{k}^{c_{k}}.P$
  a) Nếu $a$ chẵn thì toàn bộ $p_{i}, P$ lẻ. Áp dụng bổ đề LTE, ta có $v_{p_{i}}(A) = v_{p_{i}}(a^{v} - 1) - v_{p_{i}}(a - 1) = v_{p_{i}}(v)$. Nghĩa là $v = p_{1}^{d_{1}}p_{2}^{d_{2}}\cdots p_{k}^{d_{k}}Q$
  Lúc này, $A \ge a^{v - 1} + 1 = a^{p_{1}^{d_{1}}p_{2}^{d_{2}}\cdots p_{k}^{d_{k}}Q - 1} + 1 \ge 3^{p_{1}^{d_{1}}p_{2}^{d_{2}}\cdots p_{k}^{d_{k}}Q - 1} + 1 > A$. Vô lí.
  b) Nếu $a = 4t + 1$. Lúc này ta vẫn có thể áp dụng bổ đề LTE như trên do $4\mid a - 1$ nên $v_{2}(a^{v} - 1) = v_{2}(a - 1) + v_{2}(v)$. Đánh giá tương tự ta có điều vô lý.
  c) Nếu $a = 4t + 3$. Khi đó để ý nếu $v$ lẻ ta sẽ dẫn đến $v_{2}(A) = v_{2}(v) = 0$ nên đánh giá tương tự a) cho điều vô lý.
  Xét $v$ chẵn, theo bổ đề LTE $v_{2}(a^{v} - 1) = v_{2}(a - 1) + v_{2}(a + 1) + v_{2}(v) - 1 = v_{2}(a + 1) + v_{2}(v)$.
  Đặt $L = v_{2}(v)$, $K = v_{2}(A) = d_{1}$ và $J = v_{2}(a + 1) \; (J \ge 2)$. Ta có $K = v_{2}(A) = v_{2}(a^{v} - 1) - v_{2}(a - 1) = L + J - 1$ (lưu ý là do ta đã sắp xếp $p_{i}$ nên $p_{1} = 2$)
  Viết lại $A = 2^{L + J - 1}p_{2}^{d_{2}}\cdots p_{k}^{d_{k}}$ và $v = 2^{L}p_{2}^{d_{2}}\cdots p_{k}^{d_{k}}.Q$. Mặt khác, để ý là $v_{2}(a + 1) = J$ nên $a + 1 \ge 2^{J} \iff a \ge 2^{J} - 1$. Ta có:
  $$A = a^{v - 1} + a^{v - 2} + \cdots + 1 \ge a^{v - 1} + 1 \ge (2^{J} - 1)^{v - 1} + 1 = [(2^{J} - 2) + 1]^{2^{L}p_{2}^{d_{2}}\cdots p_{k}^{d_{k}}Q} + 1 \ge 2^{L}p_{2}^{d_{2}}\cdots p_{k}^{d_{k}}Q(2^{J} - 2) + 2 \ge 2^{L + J}.p_{2}^{d_{2}}\cdots p_{k}^{d_{k}} - 2^{L + 1}p_{2}^{d_{2}}\cdots p_{k}^{d_{k}} + 2 \ge A$$
  Để ý dấu đẳng thức xảy ra khi và chỉ khi $v = 2$, $a = 2^{l} - 1$.
  Từ đó ta cần đi tìm $u$ sao cho mọi ước nguyên tố của $a^{2.3^{u}} - 1$ là ước nguyên tố của $a^{3^{2016}} - 1$. Xét trường hợp $u \neq 0$, theo bổ đề 3 thì $a^{3^{u}} + 1$ có ước nguyên tố lẻ. Xét $q$ là ước nguyên tố lẻ của $a^{3^{u}} + 1$. Ta có $q\mid \frac{a^{3^{2016}} - 1}{a^{3^{u}} - 1}$, nếu ta đặt $x = a^{3^{u}}$ và $y = 3^{2016 - u}$ ($y$ lẻ) thì viết lại $q\mid \frac{x^{y} - 1}{x - 1} = x^{y - 1} + x^{y - 2} + \cdots + 1 = x^{y - 2}(x + 1) + x^{y - 4}(x + 1) + \cdots + x(x + 1) + 1$ (do $y$ lẻ) từ đó suy ra $q\mid 1$ do $q\mid x + 1$. Vô lí.
  Từ đó thu được $u = 0$ hay $n = 2$.
  Thử lại, cho ta bộ nghiệm là $(a, n) = (2^{l} - 1, 2)$
• TH2. $n > 2016$
  Xét tương tự trên, với $v > 1$ ta cũng sẽ thu được $n = 2$. Vô lí.
  Xét $v = 1$. Khi đó ta cần chứng minh có 1 ước nguyên tố là ước của $3^{3^{u}} - 1$ nhưng không là ước của $3^{3^{2016}} - 1$
  Tuy nhiên điều này không đúng vì nếu ngược lại, nghĩa là sẽ có một ước nguyên tố $q$ sao cho $v_{q}(3^{3^{u}}) > v_{q}(3^{3^{2016}})$. Nếu $q$ lẻ: mọi ước nguyên tố $q$ của $3^{3^{u}} - 1$ và $3^{3^{2016}} - 1$ đều khác $3$ nên theo bổ đề LTE $v_{q}(3^{3^{u}} - 1) = v_{q}(3^{3^{2016}} - 1) + v_{q}(3^{u - 2016}) = v_{q}(3^{3^{2016}})$
  Do đó ta chỉ cần xét $3^{3^{u}} - 1 = 2^{i}.(3^{3^{2016}} - 1)$, tuy nhiên PT này vô nghiệm do đó ta có đpcm (có thể cm bằng cách chia qua) :-)
   

P.S: Hay quá :-s, đoạn cuối đánh giá quên mất việc $a + 1 = 2^{l}$ :-P

Bài viết đã được chỉnh sửa nội dung bởi Ego: 26-03-2016 - 12:29

[Zaraki]

Mình nghĩ Ego hiểu nhầm ý đề rồi, đề bài là $\forall \; p \mid a^n-1 \implies p \mid a^{3^{2016}}-1$.

 

PS: Ego đã sửa lỗi.

Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 24-03-2016 - 20:06

[Hoang Nhat Tuan]

Hình câu a dùng tính chất đường tròn A-Apollonius và hàng điểm điều hòa là ra ạ:

Gọi $(O')$ là đường tròn đi qua $A,D$ và tiếp xúc với $OA$ thì $(O')$ trực giao với $(O)$ nên $O'$ thuộc $BC$, do đó $O'A^2=O'B.O'C=OG^2$ nên $OG$ là tiếp tuyến của $(O)$ hay tứ giác $ABGC$ điều hòa, gọi $H'$ là giao của $EF$ và $AD$, $K$ là giao của $EF$ và $BC$, theo một tính chất quen thuộc thì $(KBO'C)=-1$ nên $F(KBO'C)=(H'DAB)=B(H'DAB)=(JCAE)=-1$ (với $J$ là giao của $BH'$ với $AC$=> $M(JCAE)=-1$ mà $M(BCAG)=-1$ nên $B,J,M$ thẳng hàng, tương tự ta được $H\equiv H'$ nên $H$ nằm trên $AD$ do đó $AH$ đi qua điểm chính giữa cung $BC$ cố định.

Bài viết đã được chỉnh sửa nội dung bởi Hoang Nhat Tuan: 24-03-2016 - 22:10

[viet nam in my heart]

Bài hình ý b) nên viết lại như sau cho đẹp

 

Bài toán. Cho tam giác $ABC$ với phân giác $BE,CF$ cắt nhau tại $I$, tâm ngoại tiếp $O$. Đường thẳng qua $I$ vuông góc $OI$ cắt $BC,EF$ tại $M,N$. Chứng minh rằng $IM=2IN$.

 

Giải. Gọi $BE,CF$ cắt $(O)$ tại $P,Q$ khác $B,C$. $EF$ cắt $BC$ tại $X$. $AI$ cắt $BC,EF$ tại $Y,Z$. $MN$ cắt $PQ,AS$ tại $K,L$. Theo bài toán con bướm dễ thấy $IM=IK$. Mặt khác dễ thấy $PQ$ là trung trực $AI$. $AX$ là phân giác ngoài góc $A$ nên $IL=2IK=2IM$ hay $ML=3MI$. Lại có hàng điều hòa cơ bản $(AI,YZ)=-1$ nên $X(AI,YZ)=-1$ chiếu chùm này lên đường thẳng $MN$ thì hàng $(LI,MN)=-1$, từ đó $\frac{NL}{NI}=\frac{ML}{MI}=3$ hay $IN=\frac{1}{4}IL=\frac{1}{2}IM$. Ta hoàn thành chứng minh.

 

Theo mình ý tưởng của ý b) hay và mới, tuy nhiên cũng khá mẹo mực!

Ở trong https://nguyenvanlin...terfly-theorem/ trước đó đã có một bài toán liên quan (Bài 9).

Em cũng vừa mới đọc tài liệu này  

Còn phần a) sau khi chứng minh $ABGC$ điều hòa thì có thể sử dụng $Ceva Sin$ cũng cho ta điều phải chứng minh

 

Hình câu a dùng tính chất đường tròn A-Apollonius và hàng điểm điều hòa là ra ạ:

hình TST 2016.png

Gọi $(O')$ là đường tròn đi qua $A,D$ và tiếp xúc với $OA$ thì $(O')$ trực giao với $(O)$ nên $O'$ thuộc $BC$, do đó $O'A^2=O'B.O'C=OG^2$ nên $OG$ là tiếp tuyến của $(O)$ hay tứ giác $ABGC$ điều hòa, gọi $H'$ là giao của $EF$ và $AD$, $K$ là giao của $EF$ và $BC$, theo một tính chất quen thuộc thì $(KBO'C)=-1$ nên $F(KBO'C)=(H'DAB)=B(H'DAB)=(JCAE)=-1$ (với $J$ là giao của $BH$ với $AC$=> $M(JCAE)=-1$ mà $M(BCAG)=-1$ nên $B,J,M$ thẳng hàng, tương tự ta được $H\equiv H'$ nên $H$ nằm trên $AD$ do đó $AH$ đi qua điểm chính giữa cung $BC$ cố định.

$J$ là giao của $BH'$ với $AC$ mới đúng chứ

Bài viết đã được chỉnh sửa nội dung bởi viet nam in my heart: 24-03-2016 - 21:16

[Zaraki]

Lời giải câu a của mình khá là ngắn nên mình cũng không chắc chắn lắm, mong mọi người có thể kiểm tra hộ mình.

Lời giải sai

 

 

Ta sẽ đi chứng minh $AH$ đi qua trung điểm cung $BC$ không chứa $A$. Điều này tương đương với việc chứng minh $A,I,D$ thẳng hàng, tương đương với việc chứng minh $B(DA,HI)=C(DA,HI)$.

 

Áp dụng định lý Pascal cho hai tam giác $ANM$ và $GBC$ ta suy ra $H,E,F$ thẳng hàng.

 

Khi đó, nếu $EF \cap BC=T$ thì $(TD,BC)=(TH,FE)=-1$ suy ra $$B(DA,HI)= B(TF,HE)= 1-(TH,FE)=1-(TH,EF)=(TE,HF)=C(DA,HI).$$

 

Do đó $B(DA,HI)=C(DA,HI)$ và $B,D,C$ thẳng hàng nên suy ra $A,H,I,D$ thẳng hàng suy ra $AH$ đi qua trung điểm cung $BC$ không chứa $A$.  

 

 

Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 25-03-2016 - 07:01

[vuliem1987]

 

VN TST 2016

Thời gian thi: 4 tiếng 30 phút

Ngày 1

 

Bài 1. Tìm $a,n$ nguyên dương với $a>2$ để mỗi ước nguyên tố của $a^n-1$ cũng là ước nguyên tố của $a^{3^{2016}}-1.$

 

Bài 2. $A$ là tập $2000$ số nguyên phân biệt và $B$ là tập $2016$ số nguyên phân biệt. $K $ là số cặp $(m,n)$ có thứ tự với $m$ thuộc $A$ và $n$ thuộc $B$ mà $|m-n|\leq 1000$. Tìm max $K$?

 

Bài 3. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ có $B,C$ cố định, $A$ chuyển động trên cung $BC$ của $ (O)$. Các phân giác $AD,BE,CF$ giao nhau tại $I$. Đường tròn qua $D$ tiếp xúc với $OA$ tại $A$ cắt $(O)$ tại $G$. $GE,GF$ giao $(O)$ lần thứ hai tại $M,N$. $BM$ giao $CN$ tại $H.$

a) Chứng minh rằng $AH$ đi qua một điểm cố định.

b) $BE, CF$ giao $(O)$ lần lượt tại $K,L$. $AH$ giao $KL$ tại $P$. $Q$ là một điểm trên $EF$ sao cho $QP=QI.$ $J$ là điểm nằm trên $(BIC)$ sao cho $IJ\perp IQ$. Chứng minh rằng trung điểm $IJ$ chuyển động trên một đường tròn cố định.

 

Nguồn: MathScope.

 

Bài 2. Nếu đọc đề thì hình như các tập A và B có các phần tử có thể trùng nhau không nhỉ ? Chẳng hạn $A=\left \{ 1;2;...;2000 \right \},B=\left \{ 1;2;...;2016 \right \}$ thì đáp án là 3016880 (không biết có tính nhầm nhầm không ?)

[Zaraki]

Bài 2. Nếu đọc đề thì hình như các tập A và B có các phần tử có thể trùng nhau không nhỉ ? Chẳng hạn $A=\left \{ 1;2;...;2000 \right \},B=\left \{ 1;2;...;2016 \right \}$ thì đáp án là 3016880 (không biết có tính nhầm nhầm không ?)

Vâng, em nghĩ là $A$ và $B$ có thể có phần tử trùng nhau.

 

Em thấy chọn như thế vẫn chưa đủ lớn đâu ạ, chọn $A= \{ 9,10, \cdots , 2008 \}$ sẽ cho $K$ lớn hơn.

[quanghung86]

Bài mà Toàn giải ở đây có thể coi là tổng quát cho ý b) http://www.artofprob...unity/c6h617525

[Zaraki]

Một mở rộng cho Bài 2 a) khi cho điểm $I$ là điểm bất kì.

 

Cho tam giác $ABC$ nội tiếp $(O)$. Một điểm $P$ nằm trong tam giác. $AP,BP,CP$ lần lượt cắt $BC,CA,AB$ tại $D,E,F$. $EF$ cắt $BC$ tại $T$. Đường tròn ngoại tiếp tam giác $TAD$ cắt $(O)$ lần thứ hai tại $G$. $GE,GF$ thứ tự cắt $(O)$ lần thứ hai tại $M,N$. $CN$ cắt $BM$ tại $Q$. Chứng minh rằng $\angle BAP= \angle CAQ$.

 

Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 25-03-2016 - 04:48

[Mr Stoke]

Bài 1 nếu đã sử dụng định lý Bang-Zsigmondy thì lời giải viết ra chắc không quá 1 hoặc 2 dòng. Vì vậy cách làm của bạn Ego tối đa thì cũng chỉ được 1/7 điểm.

Bài viết đã được chỉnh sửa nội dung bởi Mr Stoke: 25-03-2016 - 06:05

[Zaraki]

Lời giải câu a của mình khá là ngắn nên mình cũng không chắc chắn lắm, mong mọi người có thể kiểm tra hộ mình.

Ta sẽ đi chứng minh $AH$ đi qua trung điểm cung $BC$ không chứa $A$. Điều này tương đương với việc chứng minh $A,I,D$ thẳng hàng, tương đương với việc chứng minh $B(DA,HI)=C(DA,HI)$.

 

Áp dụng định lý Pascal cho hai tam giác $ANM$ và $GBC$ ta suy ra $H,E,F$ thẳng hàng.

 

Khi đó, nếu $EF \cap BC=T$ thì $(TD,BC)=(TH,FE)=-1$ suy ra $$B(DA,HI)= B(TF,HE)= 1-(TH,FE)=1-(TH,EF)=(TE,HF)=C(DA,HI).$$

 

Do đó $B(DA,HI)=C(DA,HI)$ và $B,D,C$ thẳng hàng nên suy ra $A,H,I,D$ thẳng hàng suy ra $AH$ đi qua trung điểm cung $BC$ không chứa $A$.  

Lời giải này không đúng rồi, vì mình đã vô tình thừa nhận rằng $A,H,D$ thẳng hàng. 

 

Lời giải đúng: (cũng không khác Hoang Nhat Tuan là bao nhưng không phải vẽ thêm điểm phẩy nào).

 

 

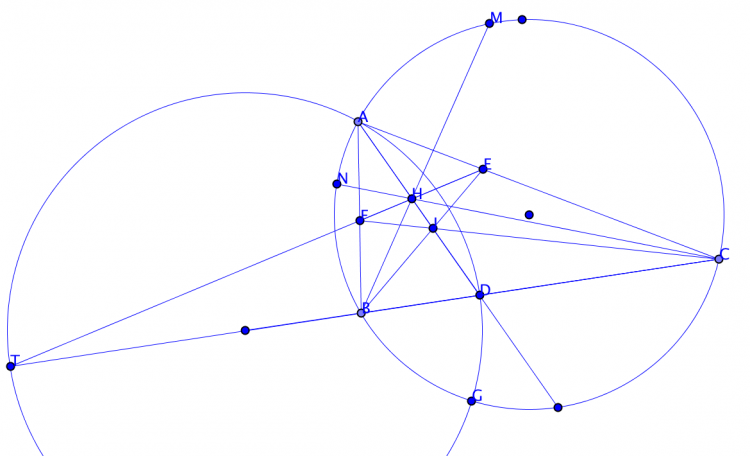
Đường tròn qua $D$ tiếp xúc với $OA$ tại $A$ chính là đường tròn $A$-Apollonius của tam giác $ABC$. Từ đây ta suy ra tứ giác $ABGC$ điều hoà, do đó $$\begin{aligned} B(DH,IA) & =B(CH,EA)= M(CH,EA) \; ( \text{do} \; \overline{A,E,D}) \\ & = M(CB,GA)=-1 = N(BC,GA) \; ( \text{do} \; ABGC \; \text{điều hoà}), \\ & = C(BH,FA)=C(DH,IA) \; (\text{do} \; \overline{A,F,B}). \end{aligned}$$

Từ đây ta suy ra $A,H,I$ thẳng hàng suy ra $AH$ đi qua trung điểm cung $BC$ không chứa $A$.

Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 26-03-2016 - 03:10

[vuliem1987]

Vâng, em nghĩ là $A$ và $B$ có thể có phần tử trùng nhau.

 

Em thấy chọn như thế vẫn chưa đủ lớn đâu ạ, chọn $A= \{ 9,10, \cdots , 2008 \}$ sẽ cho $K$ lớn hơn.

Uh em đúng rồi, tối qua khi nghĩ lại thì thấy trong cách tính số phần tử bên ngoài 2 tập gồm 2000 số thì số phần tử giảm dần, do đó để K tăng thì lấy đối xứng lại, tức đáp án em là đúng.

Có lẽ cái tinh tế của bài này là chọn 2 tập A và B, tuy nhiên cái khó là phải chứng minh điều đó và lời giải chặt chẽ. Hy vọng sớm có lời giải đầy đủ và chặt chẽ. 

[Ego]

To @Mr Stoke, em cảm ơn thầy đã nhận xét cho em. Em cũng thấy lời giải mình nếu dùng Zsigmondy mà lý luận như trên thì đúng là phức tạp thật, hơi nửa nạc nữa mỡ.
Đây là lời giải khác của em

Theo như bổ đề 1 ở trên ta sẽ thu được $\text{gcd}(a^{n} - 1, a^{3^{2016}} - 1) = a^{3^{w}} - 1$ với $w = 2016$ hoặc $w = u$ (trong đó $n = 3^{u}.v$ với $\text{gcd}(3, v) = 1$)

Giả thiết bài toán tương đương nếu $p$ là một số nguyên tố $p\mid a^{n} - 1 \implies p\mid a^{3^{w}} - 1$

• TH1. $w = u$, khi đó $3^{w}$ là ước của $n$. Nếu $w = 0$ thì áp dụng Zsigmondy thì có một ước nguyên tố $p\mid a^{n} - 1$ mà $p\nmid a^{3^{w}} - 1 = a - 1$ nếu như $v > 2$ hoặc $a \neq 3$. Từ đó ta suy ra $v = 1$ hoặc $v = 2$, riêng với $v = 2$ thì $a = 2^{l} - 1$
  Nếu $w \ge 1$ thì áp dụng Zsigmondy ta lại thu được có một ước nguyên tố $p\mid a^{n} - 1$ mà $p\nmid a^{3^{w}} - 1$ nếu như $v > 1$. Từ đó ta chỉ suy ra $v = 1$.
  Kết luận lại nghiệm, $(a, n) = (3, 2), (t, 3^{u}) \; (u < 2016)$ (điều này đúng do $a^{3^{u}} - 1 \mid a^{3^{2016}} - 1$
• TH2. $w = 2016$. Tức là $u \ge 2016$. Nếu $v > 1$ hoặc $u > 2016$ thì theo định lý Zsigmondy sẽ có một ước nguyên tố $p\mid a^{n} - 1$ mà $p\nmid a^{3^{2016}} - 1$. Do đó nghiệm là $n = 3^{2016}$.

Vậy nghiệm của bài toán là $(a, n) = (2^{l} - 1, 2), (t, 3^{u})$ với $u\le 2016$.

Spoiler

Mình nghĩ mình có một cách không dùng Zsigmondy nữa, mình sẽ sửa ở trên.

Bài viết đã được chỉnh sửa nội dung bởi Ego: 26-03-2016 - 12:20

[vuliem1987]

Tối về có thời gian đánh bài giải (Có thể lời giải vẫn chưa đủ chặt chẽ và đầy đủ) để m.n cùng thảo luận. Hy vọng có lời giải khác của m.n đơn giản hơn.

[Zaraki]

Ngày 2.

 

Bài 4. Cho tam giác $ABC$ nhọn có $\angle ACB<\angle ABC<\angle ACB+\dfrac{\angle BAC}{2}$. Lấy điểm $D$ thuộc cạnh $BC$ sao cho $\angle ADC=\angle ACB+\dfrac{\angle BAC}{2}$. Tiếp tuyến với đường tròn ngoại tiếp tam giác $ABC$ tại $A$ cắt $BC$ tại $E$. Phân giác $\angle AEB$ cắt $AD$ và cắt $(ADE)$ tại $G$ và $ F$, $DF$ giao $AE$ tại $H.$

a) Chứng minh rằng các đường tròn đường kính $AE,DF,GH$ có một điểm chung.

b) Trên phân giác ngoài $\angle BAC $ và trên tia $AC$ lần lượt lấy các điểm $K$ và $M$ sao cho $KB=KD=KM$, trên phân giác ngoài $\angle BAC$ và trên tia $AB$ lần lượt lấy các điểm $L$ và $N$ sao cho $LC=LD=LN.$ Đường tròn đi qua $M,N$ và trung điểm $I$ của $BC$ cắt $BC$ tại $P$ ($P\neq I$). Chứng minh rằng $BM,CN,AP$ đồng quy.

 

Bài 5. Cho $a_1,a_2,...,a_{n-1},a_n$ ($n\geq 3$), trong đó mỗi số $a_i $ nhận giá trị $\in \{0;1\}$. Xét $n$ bộ số $S_1=(a_1,a_2,...,a_{n-1},a_n)$, $S_2=(a_2,a_3,...,a_n,a_1)$;...;$S_n=(a_n, a_1, ..., a_{n-2},a_{n-1})$.  Với mỗi bộ số $r=(b_1,b_2,...,b_n)$, đặt $\omega(r)=b_1.2^{n-1}+b_2.2^{n-2}+...+b_n.2^0.$ Giả sử các số $\omega(S_1); \omega(S_2);...;\omega(S_n)$ nhận đúng $k $ giá trị phân biệt.

a) Chứng minh rằng $n\vdots k$ và $\omega(S_i)\vdots \dfrac{2^n-1}{2^k-1}$ $\forall i=\overline{1,n}.$

b) Kí hiệu $M$ và $m$ lần lượt là max và min của $\omega(S_1),...,\omega(S_n)$. Chứng minh rằng $M-m\geq \dfrac{(2^n-1)(2^{k-1}-1)}{2^k-1}.$

 

Bài 6. Cho các số thực phân biệt $\alpha_1,\alpha_2,...,\alpha_{16}$. Với mỗi đa thức hệ số thực $P(x)$; đặt $V(P)=P(\alpha_1)+P(\alpha_2)+...+P(\alpha_{16}).$

Chứng minh rằng tồn tại duy nhất đa thức $Q(x)$ bậc 8 có hệ số $x^8$ bằng $1$ thỏa mãn

i) $V(QP)=0$ với mọi đa thức $P$ có bậc bé hơn $8.$

ii) $Q(x)$ có $8$ nghiệm thực (tính cả bội).

 

Nguồn: MathScope.

Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 25-03-2016 - 16:40