Chủ đề này có 11 trả lời

[bich2nguyen]

đề thi

Hình gửi kèm

• 

[bangbang1412]

Thật sự mấy bạn post đề làm ơn chụp rõ rõ một tẹo nhé , hại mắt tớ lắm 

Câu 1 : 

$1)$ Tính giới hạn :

$$lim \frac{2016ncos(2017n)}{n^{2}+2017}$$

$2)$ Giải phương trình :

$$x-2\sqrt{x-2}-(x-2)\sqrt{x-1}+\sqrt{x^{2}-3x+2}=1$$

Câu 2 : 

$1)$ Để đặt mật mã cho két sắt của mình , một người đã chọn một bộ số có thứ tự gồm $7$ chữ số kí hiệu là $\overline{a_{1}a_{2}a_{3}a_{4}a_{5}a_{6}a_{7}}$ trong đó $a_{i} \in \left \{ 0,1,2,3,4,5,6,7,8,9 \right \}$ với $i = \overline{1,7}$ . Để có mật mã dễ mở người ấy đã chọn các chữ số sao cho ba số $\overline{a_{1}a_{2}a_{3}},\overline{a_{4}a_{5}a_{6}},\overline{a_{5}a_{6}a_{7}}$ giống nhau . Hỏi người ấy có bao nhiêu cách chọn mật mã ? 

$2)$ Tìm các cặp số nguyên $(x,y)$ thỏa mãn điều kiện :

$$x^{2}-10xy+29y^{2}=100$$

Câu 3 : 

$1)$ Xác định các góc tam giác $ABC$ biết $A + B = 120$ và $1 - 4sin^{2}\frac{B}{2}=\frac{b+c}{a+c}$

$2)$ Cho tam giác $ABC$ nhọn có $I$ là tâm đường tròn nội tiếp . Lấy điểm $M$ thuộc đoạn thẳng $AI$ sao cho từ $M$ kẻ đường thẳng vuông góc với $CI$ cắt đoạn thẳng $BI$ tại $N$ , từ $M$ kẻ đường thẳng vuông góc với $BI$ cắt đoạn $CI$ tại $P$ . Đường trung trực của hai đoạn thẳng $BN,CP$ cắt nhau tại $D$ , đường trung trực của hai đoạn thẳng $CP,AM$ cắt nhau tại $E$ , đường trung trực của hai đoạn thẳng $BN,AM$ cắt nhau tại $F$ . Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$ . Chứng minh rằng $O$ cũng là tâm đường tròn ngoại tiếp tam giác $DEF$ 

Câu 4 : 

$1)$ Cho dãy số $(u_{n})$ thỏa mãn $u_{1}=672$ và :

$$u_{n+1}=\frac{2016u_{n}}{(2n+3)u_{n}+2016}$$ với mọi $n \in N$

Tìm $u_{2016}$ 

$2)$ Cho $x,y,z$ là ba số thực không âm thỏa mãn $x+y+z=1$ . Tìm giá trị lớn nhất của biểu thức 

$$M = \frac{x^{2}+1}{y^{2}+1}+\frac{y^{2}+1}{z^{2}+1}+\frac{z^{2}+1}{x^{2}+1}$$

[Nguyen Van Luc]

Đề trường nào đây bạn?

[bich2nguyen]

Đề trường nào đây bạn?

chuyên Kon Tum bạn nhé

[Nguyen Van Luc]

bài 1 và bài 4_1 là cho điểm rồi 

[phamngochung9a]

$2)$ Cho $x,y,z$ là ba số thực không âm thỏa mãn $x+y+z=1$ . Tìm giá trị lớn nhất của biểu thức 

$$M = \frac{x^{2}+1}{y^{2}+1}+\frac{y^{2}+1}{z^{2}+1}+\frac{z^{2}+1}{x^{2}+1}$$

Chỉ biết chém mỗi câu này 

Không mất tính tổng quát, giả sử $x= \max\left \{ x,y,z \right \}$

Ta có: 

$M\leq x^{2}+y^{2}+2+\frac{1}{x^{2}+1}+\frac{z^{2}}{x^{2}+1}\\\leq x^{2}+y^{2}+z^{2}+2+\frac{1}{x^{2}+1}\\\leq x^{2}+\left ( y+z \right )^{2}+2+\frac{1}{x^{2}+1}\\=2x^{2}-2x+3+\frac{1}{x^{2}+1}$

 

Vậy ta chỉ cần chứng minh:   $2x^{2}-2x+3+\frac{1}{x^{2}+1}\leq \frac{7}{2}$         $\left ( * \right )$

 

Thật vậy, BĐT trên tương đương với:

$4x^{4}-4x^{3}+3x^{2}-4x+1\leq 0\\\Leftrightarrow \left ( 4x^{3}+3x-1 \right )\left ( x-1 \right )\leq 0$

 

Vì $x= \max\left \{ x,y,z \right \}$ nên $x\in \left [ \frac{1}{3};1 \right ]$, do đó:

$\left\{\begin{matrix} 4x^{3}+3x-1\geq 0 & \\ x-1\leq 0 & \end{matrix}\right.$

 

$\Rightarrow \left ( * \right )$ luôn đúng

 

Vậy $\max M=\frac{7}{2}\Leftrightarrow \left\{\begin{matrix} x=1 & & \\ y=0 & & \\ z=0 & & \end{matrix}\right.$ và các hoán vị

Bài viết đã được chỉnh sửa nội dung bởi phamngochung9a: 03-09-2016 - 11:43

[bangbang1412]

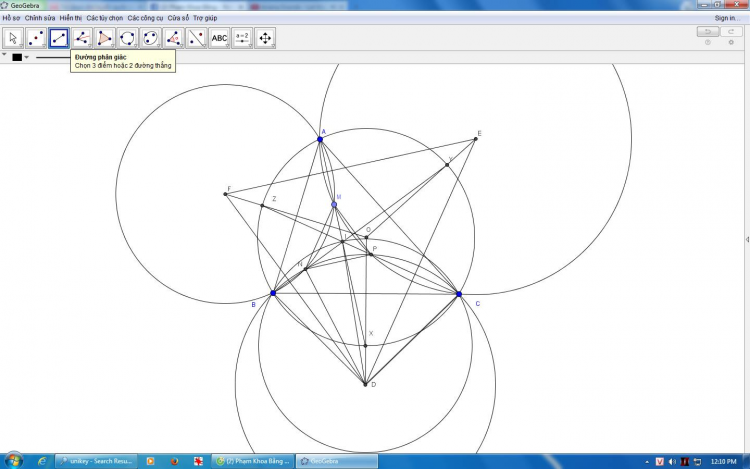
Bài hình làm theo các bước sau , mình chỉ ghi vắn tắt thôi

Cộng góc suy ra các tứ giác $NPCB,CPMA,AMNB$ là các tứ giác nội tiêp từ đó $D,E,F$ là tâm ngoại tiếp của ba đường tròn này , gọi các trung điểm cung $BC,CA,AB$ là $X,Y,Z$ . Ta sẽ chứng minh dựa trên nhận xét sau : Cho tam giác $ABC$ bất kì khi đó tồn tại duy nhất điểm $O$ thỏa mãn $\angle BOC = 2 \angle A$ và tương tự với hai cặp góc còn lại 

Ta thấy $\angle FOE = \angle YOX$ nên chỉ cần có $\angle XOY = 2 \angle EDF$ , còn $\angle EDF = \frac{1}{2}(\widehat{BC}-\widehat{BC}-\widehat{CP})$ đến đây được rồi 

thông cảm không có giấy bút khổ thế đấy 

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 03-09-2016 - 12:16

[Hai2003]

$2)$ Tìm các cặp số nguyên $(x,y)$ thỏa mãn điều kiện :

$$x^{2}-10xy+29y^{2}=100$$

$PT\Leftrightarrow (x-5y)^2+(2y)^2=100$

Viết $100$ dưới dạng tổng 2 bình phương thì $100=6^2+8^2=10^2+0^2$

Đến đây xét TH thôi.

 

PT có các nghiệm $(x;y)\in \left\{(26;4),(14;4),(-26;-4),(-14;-4),(23;3),(7;3),(-23;-3),(-7;-3),(10;0),(-10;0),(25;5),(-25;-5)\right\}$

Bài viết đã được chỉnh sửa nội dung bởi Hai2003: 03-09-2016 - 12:43

[12345678987654321123456789]

$x^{2}+y^{2}+2+\frac{1}{x^{2}+1}+\frac{z^{2}}{x^{2}+1}\leq x^{2}+y^{2}+z^{2}+2+\frac{1}{x^{2}+1}$

$x^{2}+y^{2}+2+\frac{1}{x^{2}+1}+\frac{z^{2}}{x^{2}+1}\leq x^{2}+y^{2}+z^{2}+2+\frac{1}{x^{2}+1}\;\boxed1\\\Leftrightarrow\frac{z^2}{x^2+1}\leq z^2\\\Leftrightarrow x^2+1\geq1\\\Leftrightarrow x^2\geq0\;\boxed2$

Dấu đẳng thức xảy ra ở $\boxed1$ khi và chỉ khi dấu đẳng thức xảy ra ở $\boxed2\Leftrightarrow x=0$

Anh giải thích rõ giúp em chỗ này với ạ

 

Vậy $\max M=\frac{7}{2}\Leftrightarrow \left\{\begin{matrix} \color{red}{x=1} & & \\ y=0 & & \\ z=0 & & \end{matrix}\right.$ và các hoán vị

Bài viết đã được chỉnh sửa nội dung bởi 12345678987654321123456789: 03-09-2016 - 14:45

[LAdiese]

Bái 1 câu 2 trong đề bài là file ảnh.

Gọi:

$A $: tập các mật mã có $\overline{a_{1}a_{2}a_{3}}$ giống với $\overline{a_{4}a_{5}a_{6}}$

$B $: tập các mật mã có $\overline{a_{1}a_{2}a_{3}}$ giống với $\overline{a_{5}a_{6}a_{7}}$

Ta có:

Có $10$ cách chọn cho mỗi c số $a_{4},a_{5},a_{6},a_{7}$ nên: 

$\left | A \right |=\left [ B \right ]=10.10.10.10=10^{4}$

Nhận thấy các mật mã có $\overline{a_{1}a_{2}a_{3}}$ đồng thời giống với $\overline{a_{4}a_{5}a_{6}}$ và $\overline{a_{5}a_{6}a_{7}}$ khi và chỉ khi $a_{4}=a_{5}=a_{6}=a_{7}$ lúc đó ta có:

$\left | A\cap B \right |=10$

Theo nguyên lý bù trừ, số các mật mã thỏa yc đb là:

$\left | A\cup B \right |=\left | A \right |+\left | B \right |-\left | A\cap B \right |=2.10^{4}-10=19990$

[12345678987654321123456789]

Câu 2.1:

Số cách chọn $\overline{a_1a_2a_3}$ là $10^3$

Từ đề bài ta suy ra với mỗi cách chọn $\overline{a_1a_2a_3}$ và một cách chọn $a_4$ hoặc một cách chọn $a_7$ ta có một cách chọn mật mã.

Do đó số cách chọn mật mã là : $10^3.10.2$

Tuy nhiên sẽ có một số cách chọn được lặp lại hai lần.

Đó là những cách chọn mà $\overline{a_1a_2a_3}=\overline{a_4a_5a_6}=\overline{a_5a_6a_7}\\\Leftrightarrow a_i=a_{i+1},i=\overline{1;6}$

Do đó có $10$ cách chọn lặp lại.

Vậy số cách chọn thỏa mã đề bài là : $10^3.10.2-10=19990$

[phamngochung9a]

$x^{2}+y^{2}+2+\frac{1}{x^{2}+1}+\frac{z^{2}}{x^{2}+1}\leq x^{2}+y^{2}+z^{2}+2+\frac{1}{x^{2}+1}\;\boxed1\\\Leftrightarrow\frac{z^2}{x^2+1}\leq z^2\\\Leftrightarrow x^2+1\geq1\\\Leftrightarrow x^2\geq0\;\boxed2$

Dấu đẳng thức xảy ra ở $\boxed1$ khi và chỉ khi dấu đẳng thức xảy ra ở $\boxed2\Leftrightarrow x=0$

Anh giải thích rõ giúp em chỗ này với ạ

Bạn biến đổi hơi sai một ít, chỗ $\frac{z^{2}}{x^{2}+1}\leq z^{2}$ dấu bằng xảy ra $\Leftrightarrow \left\{\begin{matrix} z=0 & \\ x=0 & \end{matrix}\right.$

 

Khi tử đã bằng $0$ thì đánh giá mẫu như thế nào cũng được