Lời giải bài toán 78.
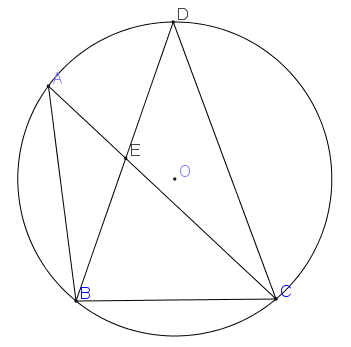
Bổ đề Cho tam giác $ABC$ có tia phân giác trong $AD$. Trên đoạn thẳng $AD$ lấy các điểm $K,L$ ($K$ nằm giữa $A$ và $L$) thỏa mãn $\angle{ACK}=\angle{LCB}$. Chứng minh rằng $\angle{ABK}=\angle{LBC}$
ScreenHunter_21 May. 04 16.29.jpg
(Bổ đề khá quen thuộc nên mình không chứng minh).
Spoiler
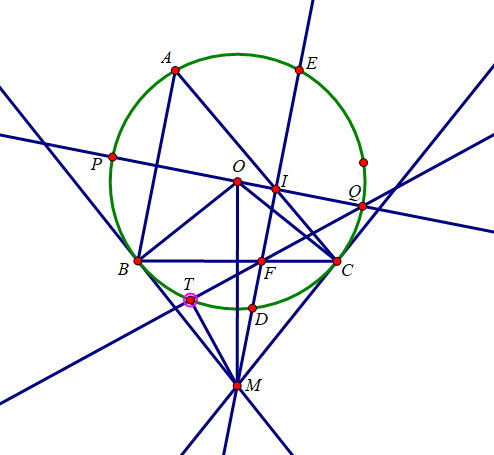
Quay trở lại bài toán
ScreenHunter_19 May. 04 16.18.jpg
Vẽ đường kính $PW$ của $(O)$. Gọi trung điểm của $BC$ là $N$. Bài toán cần chứng minh trở thành chứng minh tứ giác $BKNM$ nội tiếp. Dễ chứng minh được $N$ thuộc đường tròn đường kính $PC$.
Ta có: $\angle{ACL}=\angle{CLW}-\angle{LAC}=\angle{CLW}-\frac{\hat{A}}{2}$ $(1)$
Mặt khác $\angle{KCN}=\angle{KPN}=\angle{KPC}-\angle{WBC}$
Mà $\angle{WBC}=\frac{\hat{A}}{2}$ và $\angle{KPC}=\angle{CLW}$
$\Rightarrow \angle{KCN}=\angle{CLW}-\frac{\hat{A}}{2}$ $(2)$
Từ $(1)$ và $(2)$ suy ra $\angle{KCN}=\angle{ACL}$ $\Rightarrow \angle{ACK}=\angle{LCB}$
Áp dụng bổ đề thì ta có ngay $\angle{ABK}=\angle{LBC}$ $(3)$
$\Rightarrow \angle{ABK}=\angle{NBM}$
$\Rightarrow \angle{ABN}=\angle{KBM}$
Mà $\angle{ABN}=\angle{AWC}$ (cùng chắn $AC$)
Nên $\angle{AWC}=\angle{KBM}$ $(4)$
Từ $(3)$ ta cũng có $\angle{BKW}=\angle{ABK}+\frac{\hat{A}}{2}=\angle{LBC}+\angle{CBW}=\angle{LBW}$
$\Rightarrow \angle{BKW}=\angle{LBW}$
$\Rightarrow \triangle{BLW} \sim \triangle{KBW}$
$\Rightarrow \frac{BW}{BL}=\frac{KW}{BK}$
$\Rightarrow \frac{WC}{BM}=\frac{KW}{BK}$ $(BL=BM,BW=WC)$
$\Rightarrow \frac{WC}{KW}=\frac{BM}{BK}$ $(5)$
Từ $(4)(5)$ suy ra $\triangle{BKM} \sim \triangle{WKC}$
$\Rightarrow \angle{BKM}=\angle{WKC}$
Mặt khác $\angle{WKC}=\angle{LNB}=\angle{BNM}$ (Vì tứ giác $BLNC$ nội tiếp và $M,L$ đối xứng qua $BC$)
Suy ra $ \angle{BKM}=\angle{BNM}$ hay tứ giác $BKNM$ nội tiếp tức là $(BKM)$ đi qua trung điểm $N$ của đoạn thẳng $BC$ (đpcm)
Spoiler
Lời giải bài toán 78.
Bổ đề Cho tam giác $ABC$ có tia phân giác trong $AD$. Trên đoạn thẳng $AD$ lấy các điểm $K,L$ ($K$ nằm giữa $A$ và $L$) thỏa mãn $\angle{ACK}=\angle{LCB}$. Chứng minh rằng $\angle{ABK}=\angle{LBC}$
ScreenHunter_21 May. 04 16.29.jpg
(Bổ đề khá quen thuộc nên mình không chứng minh).
Spoiler
Quay trở lại bài toán
ScreenHunter_19 May. 04 16.18.jpg
Vẽ đường kính $PW$ của $(O)$. Gọi trung điểm của $BC$ là $N$. Bài toán cần chứng minh trở thành chứng minh tứ giác $BKNM$ nội tiếp. Dễ chứng minh được $N$ thuộc đường tròn đường kính $PC$.
Ta có: $\angle{ACL}=\angle{CLW}-\angle{LAC}=\angle{CLW}-\frac{\hat{A}}{2}$ $(1)$
Mặt khác $\angle{KCN}=\angle{KPN}=\angle{KPC}-\angle{WBC}$
Mà $\angle{WBC}=\frac{\hat{A}}{2}$ và $\angle{KPC}=\angle{CLW}$
$\Rightarrow \angle{KCN}=\angle{CLW}-\frac{\hat{A}}{2}$ $(2)$
Từ $(1)$ và $(2)$ suy ra $\angle{KCN}=\angle{ACL}$ $\Rightarrow \angle{ACK}=\angle{LCB}$
Áp dụng bổ đề thì ta có ngay $\angle{ABK}=\angle{LBC}$ $(3)$
$\Rightarrow \angle{ABK}=\angle{NBM}$
$\Rightarrow \angle{ABN}=\angle{KBM}$
Mà $\angle{ABN}=\angle{AWC}$ (cùng chắn $AC$)
Nên $\angle{AWC}=\angle{KBM}$ $(4)$
Từ $(3)$ ta cũng có $\angle{BKW}=\angle{ABK}+\frac{\hat{A}}{2}=\angle{LBC}+\angle{CBW}=\angle{LBW}$
$\Rightarrow \angle{BKW}=\angle{LBW}$
$\Rightarrow \triangle{BLW} \sim \triangle{KBW}$
$\Rightarrow \frac{BW}{BL}=\frac{KW}{BK}$
$\Rightarrow \frac{WC}{BM}=\frac{KW}{BK}$ $(BL=BM,BW=WC)$
$\Rightarrow \frac{WC}{KW}=\frac{BM}{BK}$ $(5)$
Từ $(4)(5)$ suy ra $\triangle{BKM} \sim \triangle{WKC}$
$\Rightarrow \angle{BKM}=\angle{WKC}$
Mặt khác $\angle{WKC}=\angle{LNB}=\angle{BNM}$ (Vì tứ giác $BLNC$ nội tiếp và $M,L$ đối xứng qua $BC$)
Suy ra $ \angle{BKM}=\angle{BNM}$ hay tứ giác $BKNM$ nội tiếp tức là $(BKM)$ đi qua trung điểm $N$ của đoạn thẳng $BC$ (đpcm)
Spoiler
Chứng minh 2 tam giác đồng dạng trong bổ đề ntn bạn NHoang.