Chủ đề này có 239 trả lời

[NHoang1608]

Lời giải bài toán 85

Gọi giao điểm $JN$ và $(O)$ là $K$, giao điểm $(I)$ và $JK,JC$
Vẽ tiếp tuyến chung $Jx$ của 2 đường tròn . Ta có $\angle{JNH}=\angle{JKC}=\angle{CJx}$
$\Rightarrow NH//KC$.
$\Rightarrow \angle{HNC}=\angle{NCK}$ (so le trong)
Mà $ \angle{HNC}=\angle{NJH}=\angle{KAC}$
Suy ra $\angle{NCK}=\angle{KAC}$ hay $K$ là điểm chính giữa cung $AC$

Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 09-05-2017 - 19:04

[Uchiha sisui]

Chỗ này dùng Brocard hơi quá tay, hơn nữa Brocard không được học ở chương trình toán THCS! (chứng minh định lý này cũng không đơn giản) Để giải quyết chỗ này ta nên dùng ý tưởng trục đẳng phương thì hay hơn (mình biết là khái niệm này không được học, nhưng về ý tưởng thì đơn giản và sáng sủa hơn rất nhiều!).

Đúng là vậy nhưng tuy nhiên để có lời giải của THCS thì Brocard là hợp lí anh à! Nếu học sinh THCS mà biết được khái niệm trục đẳng phương thì hơi quá ạ !

[Minhnksc]

Lời giải khác cho bài 83:

Bổ đề :Cho tam giác $ABC$ có đường cao $CC_{1}$; $BB_{1}$; $O$ là trung điểm của $BC$. Chứng minh $(BC_{1}O)$ và $(CB_{1}O)$ cắt nhau trên $AO$

(giống của bạn Mr.Cooper; mình xin không nhắc lại)

Trở lại bài toán 

Áp dụng bổ đề ta có $\overline{A;P;O}$

Gọi $I$ là giao điểm của $BB_{1}$ và $CC_{1}$; $L$ là giao điểm của $AI$ và $BC$

ta có $AI.AL=AC_{1}.AB=AP.AO \Rightarrow IPOL$ nội tiếp$\Rightarrow IP\perp AO(1)$

Gọi giao điểm của $AM$ và $(AC_{1}I)$ là $J\Rightarrow IJ\perp AJ$

Khi đó: $MJ.MA=MC_{1}.MB_{1}=MB.MC\Rightarrow J\in (ABC)$ 

giả sử $A'$ là giao điểm của $IJ$ với $(ABC)\Rightarrow AA'$ là đường kính của $(ABC)$

Từ đó dễ dàng chứng minh được $\overline{I;O;A}$

mà $JA'\perp AM$ nên $OI\perp AM$

Kết hợp với $AI\perp BC$ ta suy ra $I$ là trực tâm của $\Delta AOM\Rightarrow MI\perp AO(2)$

Từ $(1)$ và $(2)\Rightarrow \overline{M;I;P}\Rightarrow$ đpcm

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 10-05-2017 - 11:04

[Uchiha sisui]

Tiếp tục luyện công nào       !

 

Bài 86. (IMO Shortlist 2007) Cho năm điểm A, B, C, D, E thỏa mãn ABCD là hình bình hành, BDEC là tứ giác nội tiếp đường tròn. Đường thẳng (d) qua A cắt DC và BC tại F và G thỏa mãn $EF=EG=EC$. Chứng minh rằng (d) là phân giác góc A.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi Uchiha sisui: 10-05-2017 - 17:06

[Minhnksc]

Mình xin đề xuất bài toán tiếp theo (bài này ảo)

Bài 87(EGMO 2017):

Cho tam giác $ABC$ với tâm đường tròn ngoại tiếp $O$ và trọng tâm $G$. Gọi $O_{1};O_{2};O_{3}$ là điểm đối xứng của $O$ lần lượt qua $BC;AC;AB$; $G_{1};G_{2};G_{3}$ là điểm đối xứng của $G$ qua $BC;CA;AB$. Chứng minh rằng đường tròn ngoại tiếp các tam giác $O_{1}O_{2}C; O_{2}O_{3}A; O_{3}O_{1}B; G_{1}G_{2}C; G_{2}G_{3}A; G_{1}G_{3}B$ và $ABC$ có một điểm chung.

P/s: bạn Uchiha sisui sửa bài 84 thành 86 nhé.

[Uchiha sisui]

Mình xin đề xuất bài toán tiếp theo (bài này ảo)

Bài 87(EGMO 2017):

Cho tam giác $ABC$ với tâm đường tròn ngoại tiếp $O$ và trọng tâm $G$. Gọi $O_{1};O_{2};O_{3}$ là điểm đối xứng của $O$ lần lượt qua $BC;AC;AB$; $G_{1};G_{2};G_{3}$ là điểm đối xứng của $G$ qua $BC;CA;AB$. Chứng minh rằng đường tròn ngoại tiếp các tam giác $O_{1}O_{2}C; O_{2}O_{3}A; O_{3}O_{1}B; G_{1}G_{2}C; G_{2}G_{3}A; G_{1}G_{3}B$ và $ABC$ có một điểm chung.

geogebra-export (4).png

P/s: bạn Uchiha sisui sửa bài 84 thành 86 nhé.

Thanks bạn mình sửa rồi :V

[HoangKhanh2002]

Bài 86. (IMO Shortlist 2007) Cho năm điểm A, B, C, D, E thỏa mãn ABCD là hình bình hành, BDEC là tứ giác nội tiếp đường tròn. Đường thẳng (d) qua A cắt DC và BC tại F và G thỏa mãn $EF=EG=EC$. Chứng minh rằng (d) là phân giác góc A.

$\boxed{\text{Lời giải bài 86}}$

Gọi $H;N;K$ lần lượt là hình chiếu của $E$ xuống $DC;BC;BD$ $\Rightarrow \overline{H,N,K}$ (đường thẳng $Simson$)

Vì các $\Delta ECF; \Delta ECG$ cân nên $H;N$ lần lượt là trung điểm của $CF;CG$

Do đó: $KH//AF$$\Rightarrow K$là trung điểm của $BD\Rightarrow \overline{A,K,C}\Rightarrow \Delta EDB$ cân tại $E$

Từ đó: $\Rightarrow \widehat{BCE}=\widehat{BDE}=\widehat{EBD}=\widehat{ECF}\Rightarrow \widehat{EGC}=\widehat{EFC}$. Mà: $\widehat{EFG}=\widehat{EGF}\Rightarrow \widehat{CFG}=\widehat{CGF}\Rightarrow \widehat{DAF}=\widehat{FAB}$

Vậy bài toán được chứng minh

Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 10-05-2017 - 19:21

[Kagome]

Bài 83: (Sưu tầm)

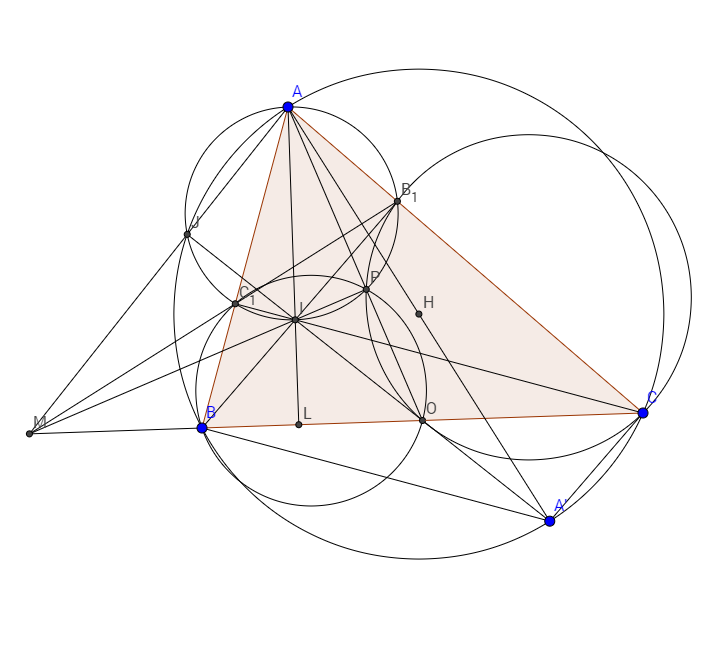
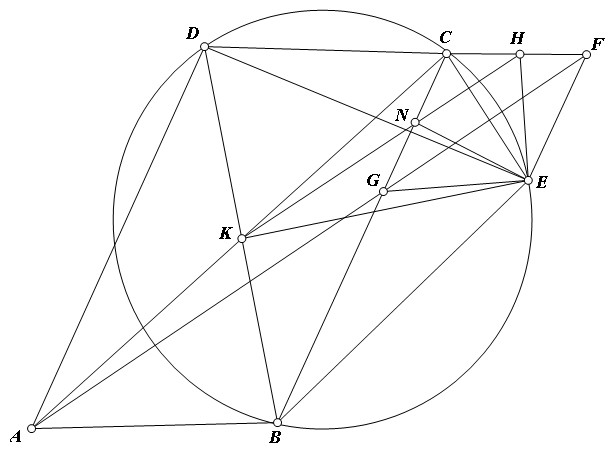
Cho tam giác $ABC$ nhọn. Các đường cao $BB_{1}; CC_{1}$. Gọi $O$ là trung điểm $BC$. Gọi $M = B_{1}C_{1} \cap BC$; $ P = (BOC_{1}) \cap (COB_{1}) $.Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

 

83.png

• Chứng minh $A,P,O$ thẳng hàng $\Rightarrow \angle HPO=90^o$

Dễ thấy 4 điểm $A,C_1,H,B_1$ cùng thuộc 1 đường tròn.

Xét tứ giác $AC_1PB_1$ có $\angle AB_1P=\angle POC,\angle AC_1P=\angle POB$ (do 2 tứ giác $C_1POB,B_1POC$ nội tiếp), $\angle POB+\angle POC=180^o \Rightarrow \angle AC_1P+\angle AB_1P=180^o\Rightarrow AC_1PB_1$ nội tiếp.

$\Rightarrow \angle APH=\angle AB_1H=90^o$

Ta có $AC_1.AB=AB_1.AC \Rightarrow B_1C_1BC$ nội tiếp $\Rightarrow \angle APB_1=\angle AC_1B_1=\angle ACB$.

Mà $\angle OCB_1+\angle OPB_1=180^o \Rightarrow \angle APB_1+\angle OPB_1=180^o \Rightarrow A,P,O$ thẳng hàng.

$\Rightarrow \angle HPO=90^o$.                                 (1)

• Chứng minh $\angle B_1C_1P=\angle PCM\Rightarrow C_1PCM$ nội tiếp.

​Ta có $\angle PC_1B_1=\angle PAB_1=\angle PAC$

Ta có $\angle OPC=\angle OB_1C=\angle B_1CO$ ($\angle OB_1C=\angle B_1CO$ do $B_1O=OB=OC$ trung tuyến ứng với cạnh huyền)

Mà $\angle OPC=\angle PAC+\angle ACP, \angle B_1CO=\angle PCO+\angle ACP$ 

$\Rightarrow \angle PAC=\angle PCO$

$\Rightarrow \angle B_1C_1P=\angle PCM \Rightarrow C_1PCM$ nội tiếp

$\Rightarrow \angle MC_1C=\angle MPC \Rightarrow 90^o+\angle MC_1B=\angle MPO+\angle OPC$

Mà $\angle MC_1B=\angle AC_1B_1=\angle B_1CO=\angle OB_1C=\angle OPC$

$\Rightarrow \angle MPO=90^o$                                  (2)

(1)(2)$\Rightarrow M,H,P$ thẳng hàng.

Vậy $MP,BB_1,CC_1$ đồng quy tại 1 điểm.

Bài viết đã được chỉnh sửa nội dung bởi Kagome: 11-05-2017 - 00:39

[Mr Cooper]

Bài Toán 88.(Sưu tầm) Cho 4 điểm A,B,C,D theo thứ tự nằm trên một đường thẳng.Gọi $\omega_1,\omega_2,\omega_3,\omega_4$ lần lượt là đường tròn bất kì qua các cặp điểm $(A,B),(B,C),(C,D),(D,A)$. $X,Y,Z,T$ lần lượt là giao điểm thứ hai của các cặp đường tròn $\omega_1​$ và $\omega_2$,$\omega_2$ và $\omega_3$,$\omega_3$ và $\omega_4$,$\omega_4$ và $\omega_1$.Khi đó $X,Y,Z,T$ cùng nằm trên một đường tròn

Bài viết đã được chỉnh sửa nội dung bởi Mr Cooper: 11-05-2017 - 11:55

[NHoang1608]

Bài Toán 88.(Sưu tầm) Cho 4 điểm A,B,C,D theo thứ tự nằm trên một đường thẳng.Gọi $\omega_1,\omega_2,\omega_3,\omega_4$ lần lượt là đường tròn bất kì qua các cặp điểm $(A,B),(B,C),(C,D),(D,A)$. $X,Y,Z,T$ lần lượt là giao điểm thứ hai của các cặp đường tròn $\omega_1​$ và $\omega_2$,$\omega_2$ và $\omega_3$,$\omega_3$ và $\omega_4$,$\omega_4$ và $\omega_1$.Khi đó $X,Y,Z,T$ cùng nằm trên một đường tròn.

Lời giải bài toán 88.

 

Ta có $\angle{XYZ}=360^{\circ}-\angle{XYC}-\angle{ZYC}= 180^{\circ}-\angle{XYC}+180^{\circ}-\angle{ZYC}$

Mà tứ giác $XYCN$ và tứ giác $YZDC$ nội tiếp cho nên $180^{\circ}-\angle{XYC}=\angle{XBC}, 180^{\circ}-\angle{ZYC}=\angle{ZDA}$

$\Rightarrow \angle{XYZ}=\angle{ZDA}+\angle{XBC}$

Lại có $\angle{XBC}=\angle{ATX}$

suy ra $\angle{XYZ}=\angle{ATX}+\angle{ZDA}$

          $\Rightarrow \angle{XYZ}+\angle{XTZ}=\angle{ATX}+\angle{XTZ}+\angle{ZDA}$

          $\Rightarrow  \angle{XYZ}+\angle{XTZ}=\angle{ATZ}+\angle{ZDA}$

          $\Rightarrow \angle{XYZ}+\angle{XTZ}=180^{\circ}$

Suy ra tứ giác $XYZT$ nội tiếp.

Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 11-05-2017 - 12:58

[viet9a14124869]

                                                                                            " Góp vui cho topic "   

Mình xin tham gia topic và mở đầu bằng hai bài toán .

Bài 89 ( APMO 2000 ): Cho tam giác ABC với trung tuyến AM và phân giác AN . Đường thẳng vuông góc với AN tại N cắt AB và AM lần lượt tại P và Q . Đường thẳng vuông góc với AB tại P cắt AN tại O . Chứng minh rằng OQ vuông góc với BC . 

Bài 90 ( sưu tầm ) : Cho tam giác ABC có I là trung điểm BC , đường thẳng d đi qua I cắt AB , AC lần lượt tại M và N , đường thẳng d' đi qua I cắt AB ,AC lần lượt tại Q và P ( M và P nàm cùng phía với BC ) . MP , NQ cắt BC tại E và F . Chứng minh rằng IE = IF .

Bài viết đã được chỉnh sửa nội dung bởi viet9a14124869: 11-05-2017 - 18:14

[moonkey01]

Mình xin được có một vài ý kiến.

 

Thiết nghĩ việc sử dụng các bài toán Olympic quá khó cho việc ôn luyện vào THPT chuyên không phải là một việc làm hay. Như bài toán của thầy Nguyễn Minh Hà được lấy từ mục "Thách đấu" trên tạp chí TTT2 tuy lời giải sử dụng kiến thức THCS nhưng không thích hợp trong điều kiện đề thi của THCS. Mình cho rằng với kỳ thi vào lớp chuyên, một bài toán hình học có ý nghĩa là khi không quá dễ, phát biểu đẹp nhưng cũng đồng thời kiểm tra được khả năng đoán nhận tính chất và nhận biết vấn đề của học sinh trong thời gian ngắn. Còn về những tính chất khó đoán nhận hơn, đó lại là câu chuyện sau khi vượt qua kỳ thi đó. Và thật ra đa số các bài toán Olympic đều có lời giải chỉ dùng kiến thức THCS.

 

Bài toán 91. Cho tam giác $ABC$ nhọn nội tiếp $(O)$. Tiếp tuyến tại $B,C$ của $(O)$ cắt nhau ở $K$. Gọi $I$ đối xứng $O$ qua $BC$. $L$ là trung điểm $OK$. Chứng minh rằng $\angle IAB=\angle LAC$.

Bài viết đã được chỉnh sửa nội dung bởi moonkey01: 11-05-2017 - 14:16

[HoangKhanh2002]

                                                                                            " Góp vui cho topic "   

Mình xin tham gia topic và mở đầu bằng hai bài toán .

Bài 89 ( APMO 2000 ): Cho tam giác ABC với trung tuyến AM và phân giác AN . Đường thẳng vuông góc với AN tại N cắt AB và AM lần lượt tại P và Q . Đường thẳng vuông góc với AB tại P cắt AN tại O . Chứng minh rằng OQ vuông góc với BC . 

Bài 90 ( sưu tầm ) : Cho tam giác ABC có I là trung điểm BC , đường thẳng d đi qua I cắt AB , AC lần lượt tại M và N , đường thẳng d' đi qua I cắt AB ,AC lần lượt tại Q và P ( M và P nàm cùng phía với BC ) . MP , NQ cắt BC tại E và F . Chứng minh rằng IE = IF .

$\boxed{\text{Lời giải bài 90}}$

PS: Bài này bạn thiếu đề tí...

Áp dụng định lí $Menelaus$ cho $\Delta ABC$ với $\overline{F,Q,N}$ ta có: $\frac{FB}{FC}.\frac{NC}{NA}.\frac{QA}{QB}=1\Rightarrow \frac{FB}{FC}=\frac{NA}{NC}.\frac{QB}{QA}$

$\Delta ABC$ với $\overline{E,P,M}\Rightarrow \dfrac{EC}{EB}.\dfrac{MB}{MA}.\dfrac{PA}{PC}=1\Rightarrow \dfrac{EC}{EB}=\dfrac{MA}{MB}.\dfrac{PC}{PA}$

$\Delta ABC$ với $\overline{Q,I,P}\Rightarrow \dfrac{PC}{PA}.\dfrac{QA}{QB}.\dfrac{IB}{IC}=1\Rightarrow \frac{PC}{PA}=\dfrac{QB}{QQ}$

Tương tự: $\Delta ABC$ với $\overline{M,I,N}\Rightarrow \dfrac{NC}{NA}.\dfrac{MA}{MB}.\dfrac{IB}{IC}=1\Rightarrow \dfrac{MA}{MB}=\dfrac{AN}{NC}$

Vậy $\frac{FB}{FC}=\frac{EC}{EB}\Rightarrow BF=CE\Rightarrow IE=IF$

Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 11-05-2017 - 17:40

[Minhnksc]

                                                                                            " Góp vui cho topic "   

Mình xin tham gia topic và mở đầu bằng hai bài toán .

Bài 89 ( APMO 2000 ): Cho tam giác ABC với trung tuyến AM và phân giác AN . Đường thẳng vuông góc với AN tại N cắt AB và AM lần lượt tại P và Q . Đường thẳng vuông góc với AB tại P cắt AN tại O . Chứng minh rằng OQ vuông góc với BC . 

Bài 90 ( sưu tầm ) : Cho tam giác ABC có I là trung điểm BC , đường thẳng d đi qua I cắt AB , AC lần lượt tại M và N , đường thẳng d' đi qua I cắt AB ,AC lần lượt tại Q và P ( M và P nàm cùng phía với BC ) . MP , NQ cắt BC tại E và F . Chứng minh rằng IE = IF .

Lời giải bài 89:

Ta có bổ đề sau:

Bổ đề: Cho tam giác $ABC$; trung điểm $K$ của $BC$; $M\in AB; N\in AC; I$ là trung điểm của $MN$ sao cho $\overline{A;I;K}$. Chứng minh $MN\parallel BC$

Qua $K$ kẻ $M'N'$ song song với $BC$ ($M'\in AB;N'\in AC$). Theo hệ quả định lý $Thalès$; ta dễ dàng suy ra $K$ là trung điểm của $MN$

+) Nếu $M'\neq M; N'\neq N \Rightarrow MM'N'M$ là hình bình hành $\Rightarrow MM'\parallel NN'$(vô lý)

Do đó $M'\equiv M; N'\equiv N\Rightarrow MN\parallel BC$ 

Trở lai bài toán:

Gọi giao điểm của $PQ$ và $AC$ là $E$
Dễ dàng chứng minh $OE\perp AC$ và tam giác $OPE$ cân ở $O\Rightarrow \hat{OPQ}=\hat{OEQ}(1)$
Qua $Q$ kẻ đường thẳng vuông góc với $OQ$ cắt $AC$ và $AB$ lần lượt ở $F$ và $D$
Từ đó ta có $OQDP$ và $OQEF$ là các tứ giác nội tiếp$\Rightarrow \hat{ODQ}=\hat{OPQ}$ và $\hat{OFQ}=\hat{OEQ}$
Kết hợp với $(1)$ ta có $\hat{ODQ}=\hat{OFQ}\Rightarrow$ tam giác $OFQ$ cân ở $O$
mà $OQ\perp FD\Rightarrow Q$ là trung điểm của $FD$

Áp dụng bổ đề; ta suy ra $FD\parallel BC$

Mà $OQ\perp FD\Rightarrow$ đpcm

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 12-05-2017 - 14:02

[Minhnksc]

"Ra lò" thêm bài nữa nào:

Bài 92:(thi thử chuyên KHTN đợt V 2012-2013)

Cho tam giác $ABC$; tiếp tuyến tại $B$ và $C$ cắt tiếp tuyến tại $A$ của đường tròn ngoại tiếp tam giác $ABC$ lần lượt ở $D$ và $E$. $CD$ cắt $AB$ ở $P$; $BE$ cắt $AC$ ở $Q$. Gọi $M$ và $N$ lần lượt là trung điểm của $CP$ và $BQ$. Chứng minh$\widehat{CBM}=\widehat{BCN}$

P/s:Nhanh thật; sắp 100 bài rồi đấy; không biết cái dự án tổng hợp các bài toán trên topic này của bác Tăng thế nào rồi nhỉ?

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 12-05-2017 - 10:57

[05479865132]

Bài 93(sưu tầm)

Cho tam giác ABC có góc A nhọn, nội tiếp đường tròn (O) và AB>AC. Tia phân giác cua góc BAC cắt đường tròn (O) tại D (D khác A) và cắt tiếp tuyến tại B của đường tròn (O) tại E. Gọi F la giao điểm của BD và AC.

a)Chứng minh EF//BC

b)Gọi M là giao điểm của AD va BC. Các tiếp tuyến tại B,D của đường tròn (O) cắt nhau tại N.Chứng minh rằng:$\frac{1}{BN}=\frac{1}{BE}+\frac{1}{BM}$

[Nguyenphuctang]

"Ra lò" thêm bài nữa nào:

Bài 92:(thi thử chuyên KHTN đợt V 2012-2013)

Cho tam giác $ABC$; tiếp tuyến tại $B$ và $C$ cắt tiếp tuyến tại $A$ của đường tròn ngoại tiếp tam giác $ABC$ lần lượt ở $D$ và $E$. $CD$ cắt $AB$ ở $P$; $BE$ cắt $AC$ ở $Q$. Gọi $M$ và $N$ lần lượt là trung điểm của $CP$ và $BQ$. Chứng minh$\hat{CBM}=\hat{BCN}$

P/s:Nhanh thật; sắp 100 bài rồi đấy; không biết cái dự án tổng hợp các bài toán trên topic này của bác Tăng thế nào rồi nhỉ?

Để coi hè làm dạo này bận quá mình đang làm cố vấn $LaTeX$ cho 1 quyển sách nên không rảnh lắm :3.

Bài 94: (Sưu tầm)

Cho tam giác $ABC$ nội tiếp $(O)$. $P$ thuộc cung nhỏ $BC$ sao cho nếu lấy $Q$ đối xứng $P$ qua $BC$ thì $Q$ nằm trong tam giác $ABC$. $QB,QC$ cắt $CA,AB$ lần lượt tại  $E,F$. $PE \cap (O) = R $ ($R$ khác $E$). Chứng minh: $BR$ chia đôi $EF$.

Khuya rồi biến vẽ hình quá. :3

[Mr Cooper]

Lời giải Bài Toán 91.

Bổ đề. Cho tam giác $XYZ$ có đường cao $XT$. $R$ là tâm đường tròn ngoại tiếp tam giác $XYZ$. Chứng minh rằng  $\angle RXZ = \angle YXT$

Chứng minh. Gọi $J$ là giao điểm thứ hai của $XR$ với đường tròn $(R)$

Dễ dàng chứng minh được $\triangle XYT \sim \triangle XJZ$ $\Rightarrow \angle RXZ = \angle YXT$

Quay trở lại bài toán.

Kẻ $AH$ vuông góc với $BC$ $(H  \in BC)$

Từ $L$ là trung điểm của $OK$ $\Rightarrow LO=LC=LB=LK$

$\Rightarrow \triangle OLC$ cân tại L $\Rightarrow \angle COL = \angle OCL$

Dễ thấy $\triangle OCI$ cân tại $C$ $\Rightarrow \angle OIC = \angle IOC = \angle OCL$

$\Rightarrow \triangle OCI \sim \triangle OLC \Rightarrow OI.OL=OC^2=OA^2$

$\Rightarrow \triangle OAI \sim \triangle OLA \Rightarrow \angle OAI = \angle OLA = \angle HAL (HA \parallel OL)$ $(1)$

Từ bổ đề trên ta có được $\angle BAH = \angle OAC$ $(2)$

Từ $(1)$ và $(2)$ $\Rightarrow \angle HAL + \angle BAH = \angle OAI +  \angle OAC \Rightarrow \angle IAC = \angle LAB \Rightarrow \angle LAC = \angle IAB $

Bài viết đã được chỉnh sửa nội dung bởi Mr Cooper: 12-05-2017 - 11:58

[Mr Cooper]

Mình đang có ý định viết tài liệu tổng hợp mấy bài Hình này, bạn nào viết chung thì trao đổi qua tin nhắn với mình :> .

 

Bài Toán 95.(Sưu tầm) Cho tam giác $ABC$ , có đường cao $AH$. $I$ là tâm đường tròn nội tiếp , $D$ là giao điểm của $(I)$ và $BC$. Kẻ $IN \perp AH$ $(N \in AH)$. Chứng minh rằng: $AI$ và $ND$ cắt nhau tại một điểm trên đường tròn ngoại tiếp tam giác $ABC$.

Bài viết đã được chỉnh sửa nội dung bởi Mr Cooper: 13-05-2017 - 17:20

[NHoang1608]

Lời giải bài 95.

Gọi giao điểm của $AI$ và $(ABC)$ là $K$, $R$ là giao điểm của $AK$ và $BC$. Ta sẽ chứng minh $N,D,K$ là 3 điểm thẳng hàng.

Ta có $\frac{ID}{AH}=\frac{IR}{AR}$  ($ID//AH$)

$\Rightarrow \frac{ID}{AN}=\frac{IR}{AI}$

Mặt khác tia $BI$ là phân giác trong tam giác $ABR$ suy ra $\frac{IR}{AI}=\frac{BR}{AB}$

$\Rightarrow \frac{ID}{AN}=\frac{BR}{AB}$   $(1)$

Lại có $\triangle{BRK} \sim \triangle{ABK}$

nên $\frac{BR}{AB}=\frac{BK}{AK}=\frac{IK}{AK}$  (Dễ chứng minh được $IK=BK$)  $(2)$

Từ $(1)$ và $(2)$ suy ra $\frac{ID}{AN}=\frac{IK}{AK}$

Kết hợp với $ID//AN$ theo định lí $Thales$ đảo ta có $N,D,K$ thẳng hàng hay $ĐPCM$.

Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 13-05-2017 - 18:03