Chủ đề này có 2 trả lời

[Zaraki]

Như vậy lời giải cho bài Tuần 2 tháng 2/2017 đã được thầy Hùng đưa ra tại đây kèm theo đó là bài toán mới. Xin trích dẫn lại bài toán mới:

 

Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. Đường tròn bàng tiếp góc $A$ là $(J)$ tiếp xúc $BC,CA,AB$ lần lượt tại $D,E,F$. $M$ là trung điểm $EF$. $DM$ cắt $(J)$ tại $N$ khác $D$. Trên đoạn $AE,AF$ lần lượt lấy các điểm $K,L$ sao cho $NK,NL$ tiếp xúc $(O)$. Chứng minh rằng tứ giác $AKNL$ ngoại tiếp.

 

[Ngockhanh99k48]

Lời giải: Dễ thấy rằng $DA$ và $DM$ đẳng giác trong góc $\angle EDF$. Ta lại có $MD. MN= ME. MF= MA. MJ$ nên $A, D, J, N$ đồng viên. Do $JN=JD$ nên $AN, AD$ đẳng giác trong góc $\angle BAC$. Kẻ đường cao $AH$. $AD$ cắt $(J)$ tại điểm thứ hai $X$. Khi đó $NX \parallel EF$. Ta có $\angle OAN = \angle HAD = 90^{\circ} - \angle CDX = 90^{\circ} - \angle NMF = \angle ANJ$.
Do đó tồn tại đường tròn $(O')$ tiếp túc trong cả hai đường tròn $(O)$ và $(J)$.
$AJ$ cắt $ON$ tại $I$. $O'I$ cắt $AN$ tại $P$. Gọi $\alpha_1, \alpha_2$ là đường tròn tâm $I$ tiếp xúc $AB, AC$ và $NL, NK$. Theo định lý $Monge-D'Alambert$, ta có $A$ là tâm vị tự ngoài của $\alpha_1$ và $(J)$, $N$ là tâm vị tự ngoài của $(J)$ và $(O')$, từ đó suy ra $P$ là tâm vị tự ngoài của $\alpha_1$ và $(O')$. Tương tự $P$ là tâm vị tự ngoài của $\alpha_2$ và $(O')$. Suy ra $\alpha_1 \equiv \alpha_2$. Như vậy $AKNL$ ngoại tiếp.

Bài viết đã được chỉnh sửa nội dung bởi Ngockhanh99k48: 19-02-2017 - 20:58

[ecchi123]

 Lời giải :

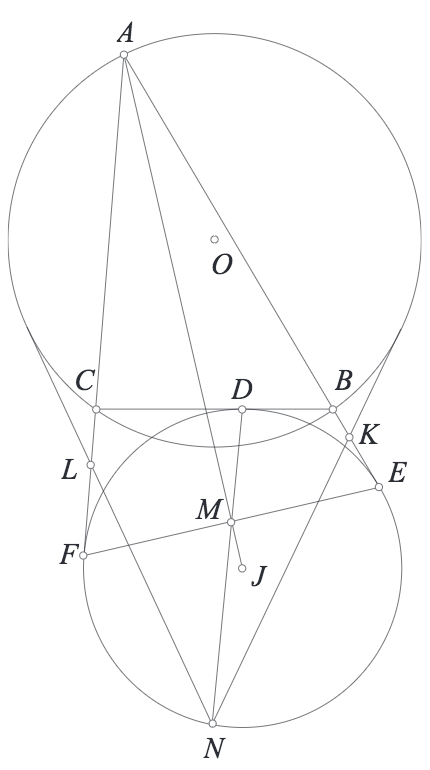
+Ta có bổ đề sau : Cho $(O),(C),(D)$ với $(C),(D)$ tiếp xúc trong với $(O)$ tại $A,B$ , Kẻ $BX,BY$ tiếp xúc với $(C)$ . $AZ,AT$ tiếp xúc với $(D)$ , Chứng minh 4 đường $BX,BY,AZ,AT$ tạo thành tứ giác ngoại tiếp

Giải : $AD$ cắt $BC$ tại $G$ , ta sẽ chứng minh $AEBF$ ngoại tiếp tâm $G$ ,( $E,F$ như hình vẽ ) gọi $r_{1},r_{2}$ là khoảng cách từ $G$ đến $BY,AZ$

Ta có :$\frac{r_1}{r_2}=\frac{BG.AC}{BC}:\frac{AG.BD}{AD}=\frac{BG}{AG}.\frac{AC}{BC}.\frac{AD}{BD}=1$ suy ra$r_{1}=r_{2}$ nên $(G,r_1)$ nội tiếp $AEBF$

+Trở lại bài toán : ta sẽ chứng minh $AN,AD$ đẳng giác trong góc $BAC$ , tức $AN$ sẽ đy qua tiếp điểm $A-Mix$ với $(O)$

- Nghịch đảo tâm $A$ phương tích bất kì ta có bài toán sau : tam giác $ABC$ nt $(O)$ , $(J)$ là $A-Mix$ tx $(O)$ tại $D$ , $(ADJ)$ cắt $(J)$ tại $N$ , khi đó $AN,AD$ đẳng giác ( điều này đúng do $JD=JN$) suy ra $AN$ sẽ đy qua tiếp điểm $A-Mix$ với $(O)$

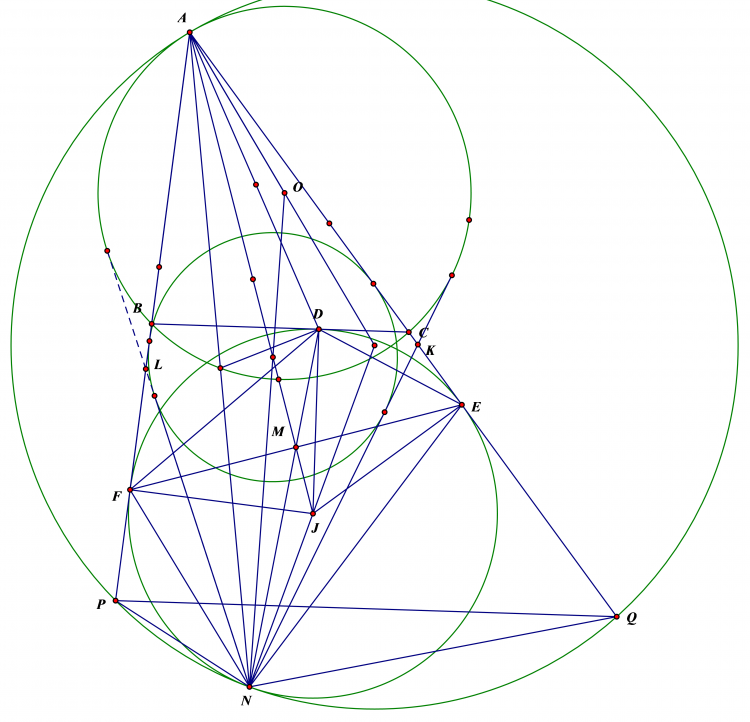
-  Xét phép vị tự tâm $A$ biến $A-Mix \mapsto (J)$... $B,C \mapsto Q,P$ như hình vẽ , Khi đó $(J)$ sẽ là đường tròn $Mixtilinear$ của tam giác $APQ$ 

Áp dụng bỏ đề với $(J)$ và $(ABC)$ cùng tiếp xúc trong với $(APQ)$ nên ta có $AKNL$ ngoại tiếp.

Bài viết đã được chỉnh sửa nội dung bởi ecchi123: 19-02-2017 - 21:55