SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 9 THCS
BÌNH ĐỊNH KHOÁ NGÀY 18 – 3 – 2017
Đề chính thức Môn thi: TOÁN
Thời gian:150 phút (không kể thời gian phát đề)
Ngày thi: 18/3/2017
Bài 1: 1) Cho biểu thức $P=\frac{2m+\sqrt{16m}+6}{m+2\sqrt{m}-3}+\frac{\sqrt{m}-2}{\sqrt{m}-1}+\frac{3}{\sqrt{m}+3}-2$
a) Rút gọn P.
b) Tìm giá trị tự nhiên của m để P là số tự nhiên.
2) Cho biểu thức P = (a + b)(b + c)(c + a) – abc với a, b, c là các số nguyên. Chứng minh rằng nếu a + b + c chia hết cho 4 thì P chia hết cho 4.
Bài 2: a) Chứng minh rằng: với mọi số thực x, y dương, ta luôn có $\frac{1}{x}+\frac{1}{y}\geq \frac{4}{x+y}$
b) Cho phương trình $2x^{2}+3mx-\sqrt{2}=0$ (m là tham số). Có hai nghiệm $x_{1}$ và $x_{2}$ .
Tìm giá trị nhỏ nhất của biểu thức $M=\left ( x_{1}-x_{2} \right )^{2}+\left ( \frac{1+x_{1}^{2}}{x_{1}}- \frac{1+x_{2}^{2}}{x_{2}}\right )^{2}$
Bài 3: Cho x, y, z là ba số dương. Chứng minh rằng $\frac{1}{x^{2}+yz}+\frac{1}{y^{2}+zx}+\frac{1}{z^{2}+xy}\leq \frac{1}{2}\left ( \frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx} \right )$
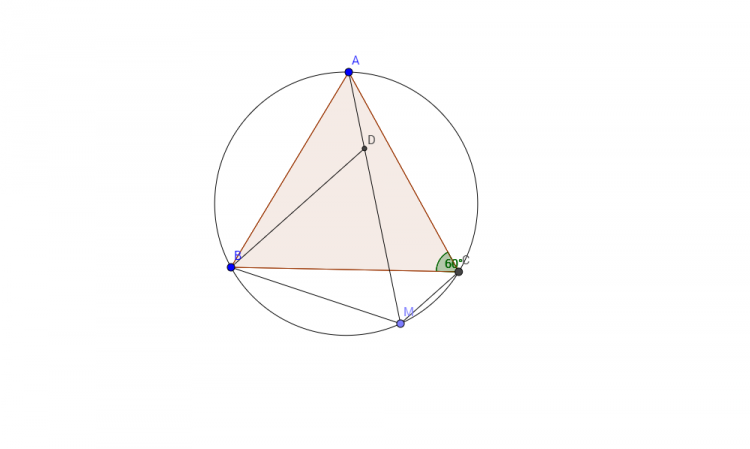
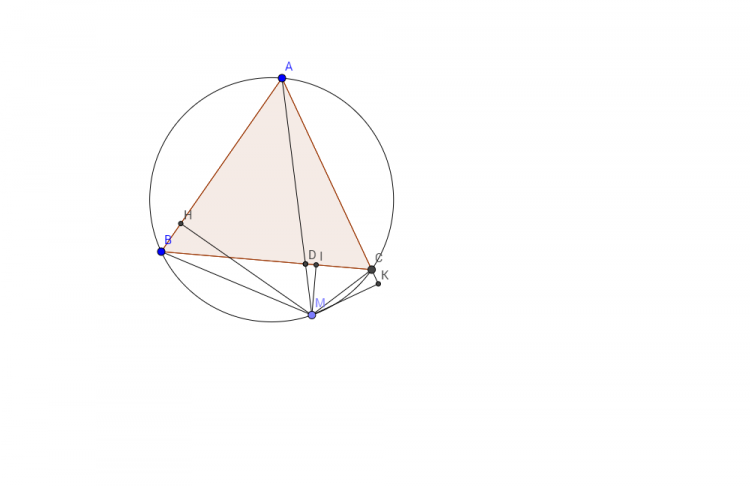
Bài 4: 1) Cho tam giác đều ABC nội tiếp đường tròn tâm O bán kính R. M là một điểm di động trên cung nhỏ BC của đường tròn đó.
a) Chứng minh MB + MC = MA
b) Gọi H, I, K lần lượt là chân đường vuông góc hạ từ M xuống AB, BC, CA. Gọi S, S’ lần lượt là diện tích của tam giác ABC, MBC. Chứng minh rằng: Khi M di động ta luôn có đẳng thức $MH+MI+MK=\frac{2\sqrt{3}(S+2S')}{3R}$
2) Cho tam giác ABC có ba góc nhọn. AD, BE, CF là các đường cao. Lấy M trên đoạn FD, lấy N trên tia DE sao cho $\widehat{MAN}=\widehat{BAC}$. Chứng minh MA là tia phân giác của góc $\widehat{NMF}$