Như vậy lời giải cho hai bài Tuần 2 tháng 6/2017 đã được đưa tại đây kèm theo là hai bài toán mới của thầy Trần Quang Hùng và các anh Ngô Quang Dương, Trần Quang Huy. Xin được trích dẫn lại hai bài toán:
Bài 1. (Trần Quang Hùng) Cho tam giác $ABC$ có các điểm $E,F$ lần lượt nằm trên các cạnh $CA,AB$. $O,K$ lần lượt là tâm ngoại tiếp các tam giác $ABC,AEF$. $AK$ cắt $BC$ tại $L$ và cắt đường tròn $(KEF)$ tại $J$ khác $K$. $EF$ cắt $BC$ tại $D$. $OD$ cắt đường tròn $(DLJ)$ tại $G$ khác $D$. Chứng minh rằng $\angle ADO= \angle OAG$.
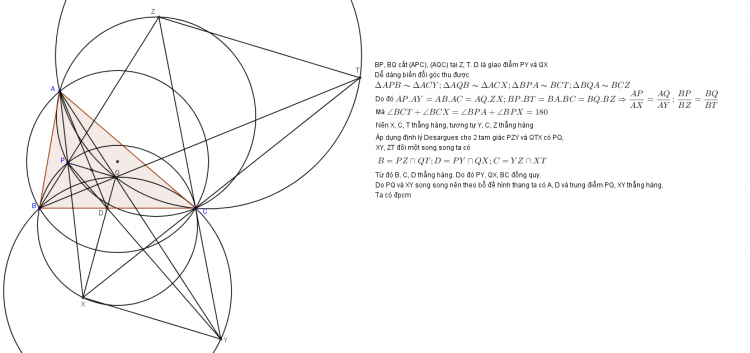
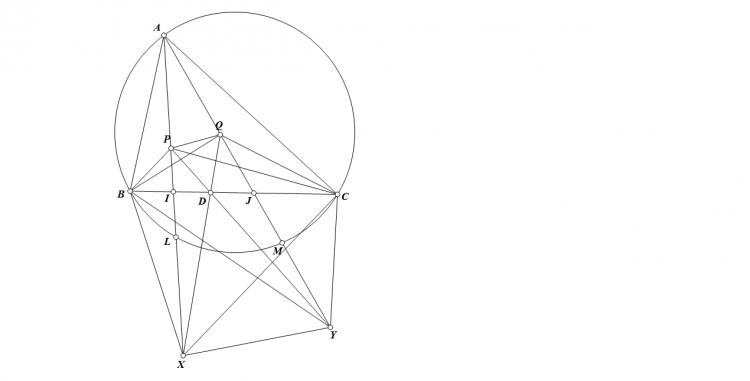
Bài 2. (Ngô Quang Dương, Trần Quang Huy) Cho tam giác $BC$ với $P,Q$ là hai điểm đẳng giác. $PA$ cắt đường tròn $(PBC)$ tại $X$ khác $P$. $QA$ cắt đường tròn $(QBC)$ tại $Y$ khác $Q$. Chứng minh rằng $QX,PY,BC$ đồng quy tại $D$ và $AD$ chia đôi $PQ$.