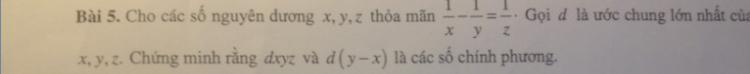Chủ đề này có 2 trả lời

[nguyenthaison]

như hình

Hình gửi kèm

• 

[Tea Coffee]

Mình làm thế này không biết có đúng không

Đặt $x=d.x_{1},y=d.y_{1},z=d.z_{1}; (x_{1},y_{1},z_{1})=1 ;x_{1},y_{1},z_{1}\epsilon Z+$

Ta có: $\frac{1}{x}-\frac{1}{y}=\frac{1}{z}=>\frac{1}{d}(\frac{1}{x_{1}}-\frac{1}{y_{1}})=\frac{1}{d}.\frac{1}{z_{1}}=>\frac{1}{x_{1}}-\frac{1}{y_{1}}=\frac{1}{z_{1}}=>y_{1}-x_{1}=\frac{x_{1}y_{1}}{z_{1}}\epsilon Z=>x_{1}y_{1}\vdots z_{1}=> \begin{bmatrix}z_{1}=1 \\ y_{1}=z_{1} \end{bmatrix}$

Ta dễ dàng chứng minh được $x_{1}$ không thể bằng $z_{1}$

+) T/h 1: $z_{1}=1$

=> $\frac{y_{1}-x_{1}}{y_{1}x_{1}}=\frac{1}{z_{1}}=1=>y_{1}-x_{1}=y_{1}.x_{1}=>\left\{\begin{matrix}y_{1}-x_{1}\vdots y_{1} \\ y_{1}-x_{1}\vdots x_{1} \end{matrix}\right. <=>\left\{\begin{matrix}y_{1}\vdots x_{1} \\ x_{1}\vdots y_{1} \end{matrix}\right. =>y_{1}=x_{1}$

Ta có: $dxyz=d.dx_{1}.dy_{1}.dz_{1}=d^{4}.x_{1}y_{1}=d^{4}.x_{1}^{2}; d(y-x)=d^{2}(y_{1}-x_{1})=d^{2}.x_{1}y_{1}=d^{2}.x_{1}^{2}$ => thỏa mãn

+) T/h 2:chắc chứng minh $x_{1}$ là SCP là được nhưng hiện tại đầu ong ong + dốt nát nên chưa nghĩ ra 

Bài viết đã được chỉnh sửa nội dung bởi Tea Coffee: 27-09-2017 - 23:27

[duylax2412]

 

Ta có: $\frac{1}{x}-\frac{1}{y}=\frac{1}{z}=>\frac{1}{d}(\frac{1}{x_{1}}-\frac{1}{y_{1}})=\frac{1}{d}.\frac{1}{z_{1}}=>\frac{1}{x_{1}}-\frac{1}{y_{1}}=\frac{1}{z_{1}}=>y_{1}-x_{1}=\frac{x_{1}y_{1}}{z_{1}}\epsilon Z=>x_{1}y_{1}\vdots z_{1}=> \begin{bmatrix}z_{1}=1 \\ y_{1}=z_{1} \end{bmatrix}$

 

 

$x_1y_1 \vdots z_1$ mà chúng chưa nguyên tố cùng nhau mà sao lại suy ra $z_1=1$?. Ví dụ ta có $gcd(7,6,3)=1$

mà $gcd(7.6,3)=3$

Thử giải như sau:

Gọi $d=(a,b,c)$ ta quy về bài toán sau:

Cho $a,b,c \in Z^{+}$ mà thỏa $(a,b,c)=1$ và $\frac{1}{a}-\frac{1}{b}=\frac{1}{c}$

Chứng minh $abc$ và $b-a$ là số chính phương

Biến đổi giả thiết thì chúng ta được $(b-a)c=ab$

Đặt $(a,b)=k \Rightarrow a=km;b=kn$ với $m,n \in Z^{+},m<n,gcd(m,n)=1$ thay vào ta có:

$(n-m)c=kmn$ Suy ra $kmn \vdots (n-m)$ và $(n-m)c \vdots k$

Do $(m,n)=1 \Rightarrow (mn,n-m)=1 \Rightarrow k \vdots n-m$ $(1)$

Nếu  $(c,k)>1$ thì khi đó $a,b,c$ có ước chung $>1$ (Vô lý) vậy nên $(c,k)=1$ dẫn đến $n-m \vdots k$ $(2)$

Từ $(1)$ và $(2)$ suy ra $n-m=k$ nên $b-a=k(n-m)=k^2$ là $SCP$ kéo theo $abc=(b-a)c^2$ cũng chính phương