Như vậy lời giải cho hai bài Tuần 2 tháng 10/2017 đã được tại đây kèm theo là hai bài toán mới của thầy Trần Quang Hùng và thầy Trần Minh Ngọc. Xin được trích dẫn lại hai bài toán:
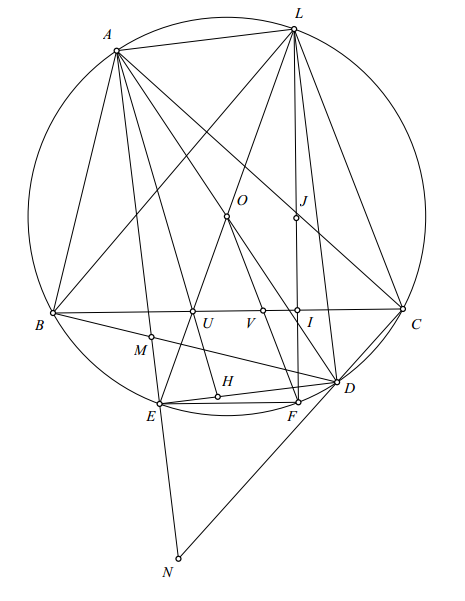
Bài 1. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và có tâm nội tiếp $I$. $P$ là một điểm nằm trong tam giác sao cho $\angle PBA= \angle PCA$. $D,E,F$ là hình chiếu của $P$ lên $BC,CA,AB$. Trên $CA,AB$ lấy $M,N$ sao cho $IM \parallel PB, IN \parallel PC$. $MN$ cắt $(O)$ tại $Q,R$. $QI,RI$ cắt lại $(O)$ tại $K,L$. Các đường thẳng qua $B,C$ lần lượt song với $DF,DE$ cắt nhau tại $J$. Chứng minh rằng $IJ \perp KL$.
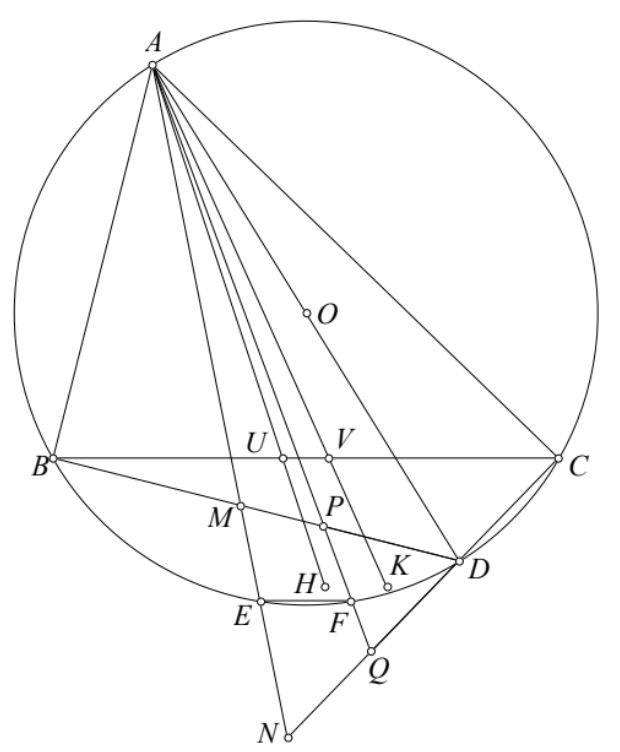
Bài 2. Cho tam giác $ABC$ nội tiếp đường $(O)$ đường kính $AD$. $E,F$ thuộc $(O)$ sao cho $EF \parallel BC$. $AE$ cắt $DB,DC$ tại $M,N$. $AF$ cắt $DB,DC$ tại $P,Q$. Gọi $H,K$ lần lượt là trực tâm các tam giác $DMN$ và $DPQ$. $AH,AK$ cắt $BC$ tại $U,V$. Chứng minh rằng $BU=CV$.
Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 15-10-2017 - 20:38