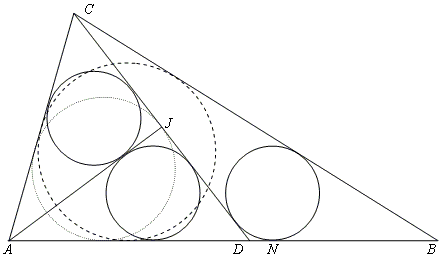
Cho tam giác cân $\it{\Delta }\,\text{ABC}$ tại đỉnh $\text{B}$ $\it{.}$ Nếu ta chọn được $\it{:}$ $\text{D}$ trên $\text{AB}$ $\it{,}$ $\text{J}$ trên $\text{DC}$ sao cho $\it{:}$ $\text{AJ}\,\it{\dashv }\,\text{CD}$ và các đường tròn nội tiếp của $\it{\Delta }\,\text{ACJ},\,\it{\Delta }\,\text{ADJ},\,\it{\Delta }\,\text{BCD}$ có cùng bán kính $\it{r}$ : Thì $\it{4}\,\it{r}= \text{AJ}$ $\it{.}$

$$\it{4}\,\it{r}= \text{AJ}$$
#1
 Đã gửi 29-01-2019 - 09:44
Đã gửi 29-01-2019 - 09:44

#2
 Đã gửi 07-02-2019 - 16:52
Đã gửi 07-02-2019 - 16:52

Gọi tâm các đường tròn nội tiếp các tam giác $AJC,AJD,BCD$ là $I_1,I_2,I_3;(I_2)$ tiếp xúc $CD$ tại $G.$
Do $R_{I_1}=R_{I_2} \Rightarrow I_1I_2 \parallel CD \Rightarrow AJ \perp I_1I_2 \Rightarrow (I_1),(I_2),AJ$ đồng quy tại $E \Rightarrow AD=AC.$
Đặt $AE=kr,k \in \mathbb{R^+}.$ Do $\Delta ABC$ cân tại $B \Rightarrow AJ>JC \Rightarrow k>2+ \sqrt{2}.$
Xét $\Delta AJD:r^2= \frac{AE.JG.GD}{AE+JG+GD}= \frac{k.GD.r^2}{r+kr+GD} \Rightarrow GD= \frac{k+1}{k-1}.r.$
Tiến hành tính toán, ta được:
$JD=r+GD= \frac{2k}{k-1}.r;CD=2JD= \frac{4k}{k-1}.r;AD=AE+GD= \frac{k^2+1}{k-1}.r; \sin \widehat{JAD}= \frac{JD}{AD}= \frac{2k}{k^2+1};$
$\cos \widehat{JAD}= \frac{JA}{AD}= \frac{k^2-1}{k^2+1}; \cos \widehat{CAD}= \cos (2 \widehat{JAD})= \cos ^2 \widehat{JAD}- \sin ^2 \widehat{JAD}= \frac{k^4-6k^2+1}{k^4+2k^2+1};$
$BC=AB= \frac{AC/2}{\cos \widehat{CAD}}= \frac{k^2+1}{k-1}. \frac{k^4+2k^2+1}{2k^4-12k^2+2}.r;BD=AB-AD= \frac{k^2+1}{k-1}. \frac{-k^4+14k^2-1}{2k^4-12k^2+2}.$
Đặt $x$ là nửa chu vi $\Delta BCD$ thì $x= \frac{BC+CD+DB}{2}= \frac{4kr(k-1)^2(k^2+4k+1)}{(k-1)(2k^4-12k^2+2)}.$
Lại có $\tan \frac{\widehat{BDC}}{2}= \tan \widehat{GDI_3}= \cot \widehat{GDI_2}= \frac{GD}{r}= \frac{k+1}{k-1};$ do đó xét $\Delta BCD:$
$r=(x-BC) \tan \frac{\widehat{BDC}}{2}= \frac{r[4k(k-1)^2(k^2+4k+1)-(k^2+1)^3]}{(k-1)(2k^4-12k^2+2)}. \frac{k+1}{k-1}$
$\Leftrightarrow 2(k-1)^2(k^4-6k^2+1)=4k(k+1)(k-1)^2(k^2+4k+1)-(k+1)(k^2+1)^3$
$\Leftrightarrow (k+1)(k^2+1)^3=2(k-1)^2(k^4+10k^3+16k^2+2k-1)$
$\Leftrightarrow k^7+k^6+3k^5+3k^4+3k^3+3k^2+k+1=2k^6+16k^5-6k^4-40k^3+22k^2+8k-2$
$\Leftrightarrow k^7-k^6-13k^5+9k^4+43k^3-19k^2-7k+3=0$
$\Leftrightarrow (k-3)(k^6+2k^5-7k^4-12k^3+7k^2+2k-1)=0.$
Do $k>2+ \sqrt{2} \Rightarrow k=3 \Rightarrow AJ=4r.$ Ta có đpcm.
- DOTOANNANG yêu thích
Sự học như con thuyền ngược dòng nước, không tiến ắt phải lùi.
Được gắn nhãn với một hoặc nhiều trong số những từ khóa sau: pythagoras, trigonometric*solution

|
Toán Trung học Cơ sở →
Hình học →
Chứng minh định lý Pythagoras theo cách dễ nhất!Bắt đầu bởi Hoang Huynh, 19-09-2021 |
|

|
|

|
Toán Trung học Phổ thông và Thi Đại học →
Bất đẳng thức và cực trị →
$$\sum\it{\sin\,A}$$ $\it{\sin}\it{(}\,\,\it{A}- \it{C}\,\,\it{)}\geqq$Bắt đầu bởi DOTOANNANG, 29-01-2019 |
|

|
|

|
Toán Trung học Phổ thông và Thi Đại học →
Bất đẳng thức và cực trị →
$\it{4}\it{\cos\,A}+ \it{3}\it{\cos\,B}+ \it{2}\it{\cos\,C}> \it{1}$Bắt đầu bởi DOTOANNANG, 29-01-2019 |
|

|
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh