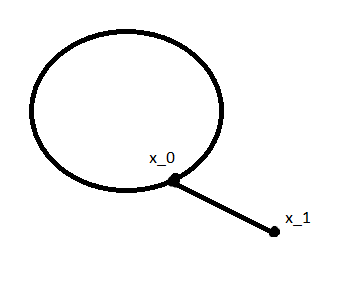Đây là bài viết đầu tiên của mình về topo đại số trên diễn đàn, và sẽ là topic mình sẽ tổng hợp lại bài từ cái webinar nho nhỏ của tụi mình trong khoảng thời gian sắp tới. Bài đầu tiên sẽ do mình đăng, các bài sẽ chủ yếu dựa trên quyển Topo đại số của Rotman.
Trước hết, mình sẽ trình bày về các khái niệm đồng luân, null- homotopic, contractible và topo thương.
1. Đồng luân
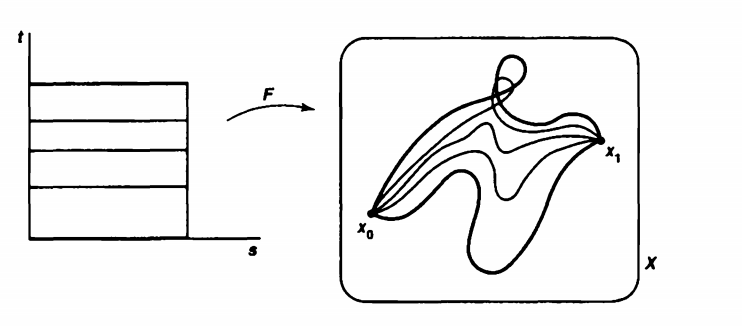
Định nghĩa 1.1. Xét \(X,Y\) là hai không gian topo và hai ánh xạ liên tục \(f, g: X\rightarrow Y\). Khi đó \(f\) gọi là đồng luân với \(g\) nếu như tồn tại một ánh xạ liên tục \(F: X\times I \rightarrow Y\) mà \(F(x,0) = f(x)\) và \(F(x,1) = g(x)\). Kí hiệu \(f\simeq g\).
Nếu như \(f\) đồng luân với \(g\) thì có thể ví như có thể dời, làm biến dạng từ \(f\) được thành \(g\), và \(f_{t}(x)=F(x,t)\) miêu tả sự "biến dạng" tại thời điểm t.
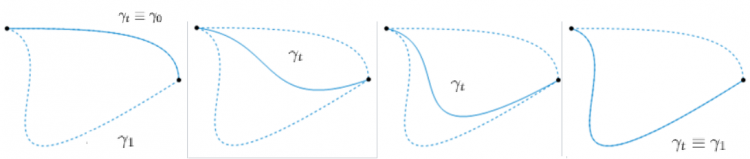
Ví dụ: Xét \(\gamma_{i}:I\rightarrow \mathbb{C}\) với \(i=0,1\) là hai hàm liên tục mà ảnh của chúng là hai đường cong trong mặt phẳng phức. Nếu ta xét \(F(x,t)=t\gamma_{1}(x)+(1-t)\gamma_{0}(x)\) thì dễ thấy \(\gamma_{0}\simeq \gamma_{1}.\)
Bổ đề 1.2. Giả sử không gian X là hợp hữu hạn các tập đóng \(X_i\) và \(f_i\) là các ánh xạ liên tục từ \(X_i\) vào \(Y\) thỏa mãn \(f_i(X_i \cap X_j) = f_j(X_i \cap X_j)\) thì tồn tại duy nhất \(f: X \rightarrow Y\) liên tục mà \(f|X_i = f_i\).
Chứng minh
Hiển nhiên từ X là hợp của các tập \(X_i\) và \(f_i(X_i \cap X_j) = f_j(X_i \cap X_j)\) ta thấy rằng ánh xạ f được xác định duy nhất.
Giả sử C là một tập đóng của Y, khi đó:
\[ f^{-1}(C) = f^{-1}(\bigcup C \cap f(X_i)) = \bigcup f^{-1}(C \cap f(X_i)) = \bigcup f^{-1}_i(C \cap f_i(X_i)).\]
Vì \(C \cup f_i(X_i)\) đóng trong \(f_i(X_i)\) nên \(C \cup f_i(X_i)\) đóng trong \(X_i\). $\square$
Từ đó ta có \(f^{-1}(C)\) và suy ra f liên tục.
Định lý 1.3. Đồng luân là một quan hệ tương đương trên tập các ánh xạ liên tục đi từ X vào Y.
+ Tính phản xạ: Xét \(F(x,t) = f(x) \forall (x,t) \in X\times I\), rõ ràng \(F\) liên tục nên \(f\simeq f\).
+ Tính đối xứng: Nếu \(F(x,t)\) liên tục, \(F(x,0) = f(x)\) và \(F(x,1) = g(x)\) thì \(G(x,t) = F(x,1-t)\) liên tục, \(G(x,0) = F(x,1) = g(x)\) và \(G(x,1) = F(x,1) = f(x)\). Do đó nếu \(f\simeq g\) thì \(g\simeq f\).
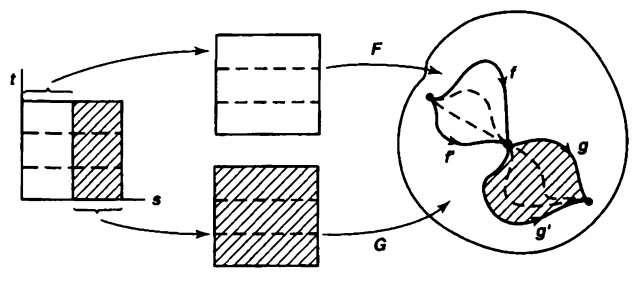
+ Tính bắc cầu: Giả sử \(F:f\simeq g\) và \(G:g\simeq h\). Khi đó xác định:
\[H(x,t)=\left\{\begin{matrix} F(x,2t),\quad \forall 0\leq t \leq \frac{1}{2} \\ G(x, 2t -1),\quad \forall \frac{1}{2} \leq t \leq 1.\end{matrix}\right.\]
Ta có \(H(x,0) = f(x)\) và \(H(x,1) = g(x)\). Hơn nữa H liên tục là hệ quả trực tiếp từ bổ đề 1.2, do đó \(f\simeq h\). $\square$
Định nghĩa 1.4. Nếu \(f: X\rightarrow Y\) là ánh xạ liên tục thì lớp tương đương đồng luân được định nghĩa như sau:
\[ [f]=\{\text{ánh xạ g liên tục từ X vào Y}: f\simeq g\}.\]
Để kết luận rằng đồng luân là một congruence trên \(\textbf{Top}\) thì ta chỉ còn cần chứng minh định lý sau:
Định lý 1.5. Cho \(f_i: Y\rightarrow Z\) và \(g_i: X\rightarrow Y\) với \(i=0,1\) là các ánh xạ liên tục thỏa mãn \(f_0 \simeq f_1\) và \(g_0 \simeq g_1\). Khi đó \([f_0\circ g_0] = [f_1 \circ g_1]\).
Chứng minh
Đầu tiên ta khẳng định rằng \(f_{0}\circ g_{0} \simeq f_{1}\circ g_{0}\).Giả sử \( F:f_{0}\simeq f_{1}\) Xét \(G(x,t)=F(g_0(x),t)\) và C là tập mở trong Y, từ đó ta có \(F^{-1}(C)\) mở trong \(X\times I\).
Khi đó \(X\times I\) có cơ sở là \(U\times V\) với U và V lần lượt là tập mở trong X và trong I. Hơn nữa, nếu đặt \(h(x,t)=(g_0(x),t)\) thì \(G=F\circ h\) và:
\[ h^{-1}(U\times V)= \bigcup_{t\in V}h^{-1}(U\times \{t\}) =\bigcup_{t\in V}g^{-1}_{0}(U)\times\{t\} = g^{-1}_{0}(U)\times V \]
mở trong\(X\times I\).
Do đó G là một ánh xạ liên tục, từ đó dễ dàng suy ra \(f_{0}\circ g_{0} \simeq f_{1}\circ g_{0}\). Tương tự, ta cũng có \(f_{1}\circ g_{0} \simeq f_{1}\circ g_{1}\) và định lý được chứng minh. $\square$
Hệ quả 1.6. Đồng luân là một congruence trên $\textbf{Top}$
Khi đó ta xây dựng được một phạm trù thương trên \(\textbf{Top}\) với \(Hom(X,Y)=[X,Y]\) và phép hợp hai cấu xạ \([f]\circ [g]=[f\circ g]\).
Phạm trù thương được xác định như trên được gọi là phạm trù thương đồng luân, và được kí hiệu là \(\textbf{hTop}\).
2. Null-homotopic và định lý cơ bản của đại số
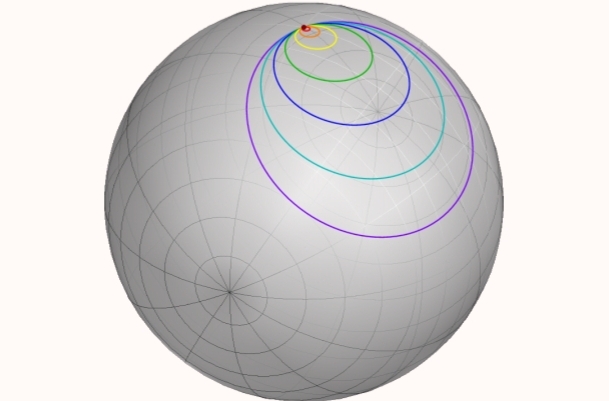
Định nghĩa 2.1. Ánh xạ k được gọi là ánh xạ hằng trên $X$ nếu tồn tại \(y\in Y\) sao cho \(k(x)=y\) với mọi \(x\in X\). Một ánh xạ \(f:X\rightarrow Y\) liên tục được gọi là null-homotopic nếu tồn tại ánh xạ hằng \(k\) trên $X$ mà \(f\simeq k\).
Nói cách khác, một ánh xạ $f$ là null-homotopic nếu như nó "co được" về một điểm.
Định lý 2.2. Cho \(f:\mathbb{S}^{n}\rightarrow Y\) là ánh xạ liên tục vào không gian Y nào đó. Các điều kiện sau là tương đương:
- f là null-homotopic
- f có thể thác triển thành một ánh xạ liên tục \(g:\mathbb{D}^{n}\rightarrow Y\)
- Nếu \(x_0 \in S^{n}\) và \(k:\mathbb{S}^{n}\rightarrow Y\) là ánh xạ hằng tại \(f(x_0)\) thì tồn tại một đồng luân \(F:f\simeq k\) với \(F(x_0,t) = f(x_0)\) với mọi \(t\in I\)
Chứng minh
\((1) \Rightarrow (2)\): Xét \(F: f\simeq k\) với k là ánh xạ hằng, \(k(x)=a\) với mọi $x$. Định nghĩa:
\[g(x)=\left\{\begin{matrix} a, \quad \forall 0\leq ||x|| \leq \frac{1}{2} \\F\big(\frac{x}{||x||},2-2||x||\big),\quad \forall \frac{1}{2}\leq ||x|| \leq 1.\end{matrix}\right.\]
Dễ thấy rằng \(g\) liên tục nhờ bổ đề 0.2
\((2)\Rightarrow (3)\):Xét \(F(x,t) = g((1-t)x + tx_{0})\). Ta kiểm tra lại được rằng F liên tục, \(F(x,0) =f(x)\) và \(F(x,1) = f(x_{0}\) nên \(F: f\simeq k\). Hơn nữa \(F(x_0,t)=g(x_{0})=f(x_{0})\)
\((3)\Rightarrow (1)\): Hiển nhiên. $\square$
Định lý 2.3. Giả sử \(\Sigma_{\rho}\subset \mathbb{C}\) là đường tròn tâm 0 bán kính \( \rho\) và kí hiệu \(f^{n}_{\rho}:\Sigma_{\rho} \rightarrow \mathbb{C}-\{0\}\) là hạn chế của \(z\mapsto z^{n}\) trên \(\Sigma_{\rho}\). Nếu không có ánh xạ \(f^{n}_{\rho}\) nào là null-homotopic thì định lý cơ bản của đại số là đúng.
Chứng minh
+) Xét đa thức \(g(x)= x^{n}+...+a_{0}\). Ta xây dựng ánh xạ đồng luân giữa \(g\) hạn chế trên \(\Sigma_{\rho}\) và \(\rho >0\) nào đó và \(f^{n}_{\rho}\) sau:
\[ F(x,t)= x^{n}+ (1-t)(a_{n-1}x^{n-1}+...+a_{0}). \]
Khi đó rõ ràng \(F\) liên tục, \(F(x,0)= g(x)\) và \(F(x,1) =f^{n}_{\rho}(x)\). Giờ ta chỉ cần chứng minh \(g_{t}(x) := F(x,t)\) nằm hoàn toàn trong \(\mathbb{C}-\{0\}\) là xong.
Thật vậy, chọn \(\rho\) sao cho \(\rho > 1 + max_{1\leq i\leq n}\big|a_{i}\big|\). Giả sử tồn tại x,t mà \(F(x,t)=0\), ta có:
Điều này không thể xảy ra vì \(\rho >0\).
+) Giả sử \(g\) không có nghiệm phức, khi đó xét \(G(x,t)=g((1-t)x)\). Vì \(g\) không có nghiệm phức nên \(G\) nằm hoàn toàn trong \(\mathbb{C}-\{0\}\). Dễ thấy rằng \(G:g|\Sigma_{\rho}\simeq k\) với \(k:z\mapsto a_{0}\). Do đó ta phải có \(f^{n}_{\rho}\simeq k\), tức \(f^{n}_{\rho}\) là null - homotopic.
Điều này mâu thuẫn với điều ta giả sử. $\square$
3. Contractible và không gian thương
Định nghĩa 2.4. Tập con $X$ của \(\mathbb{R}^{n}\) được gọi là lồi nếu với mọi \(x,y\in X\) và \(t\in I\) thì \(tx+(1-t)y\in X\).
Định nghĩa 2.5. $X$ được gọi là contractible nếu \(1_{X}\) là null-homotopic.
Một cách không chặt chẽ, ta có thể nói rằng không gian $X$ là contractible nếu nó "co được" về một điểm.
Định lý 2.6. Nếu $X$ lồi thì $X$ cũng là contractible.
Chứng minh
Xét \(x_{0}\in X\) và \(F(x,t)=tx + (1-t)x_{0}\), vì X lồi nên ta luôn có \(tx+(1-t)x_{0}\in X\). Khi đó dễ thấy rằng \(F:1_{X}\simeq k\) với k là ánh xạ hằng trên X và \(k(x)=x_{0}\) . $\square$
Định nghĩa 2.7. Xét $X$ là một không gian topo và \(Y=\{X_{i}\}\) là một phân hoạch của $X$. Lúc này, ánh xạ tự nhiên của $X$ là \(v:X\rightarrow Y\) được xác định bởi \(v(x)=X_{i}\) và topo trên $Y$ gồm họ các tập $U$ mà \(v^{-1}(U)\) mở trong $X$ được gọi là topo thương trên $Y$.
Ta quan tâm hai trường hợp đặc biệt sau đây:
+ Nếu xét $A$ là một tập con của $X$ thì phân hoạch của $X$, kí hiệu là $X/A$ gồm các tập con một phần tử của \(X-A\) và chính tập $A$. Khi đó không gian thương $X/A$ được tạo bởi "chập" các điểm của $A$ trong $X$ thành một điểm
+ Trường hợp thứ hai là xét một quan hệ tương đương \(\sim\) trên $X$ và phân hoạch $Y$ chính là họ các lớp tương đương của quan hệ \(\sim\). Khi đó ánh xạ $v$ được xác định bởi \(v:x\mapsto [x]\) Không gian thương trên $Y$ khi đó được kí hiệu bởi \(X/\sim\) .
Ví dụ:
Ta xét một ví dụ về topo thương sử dụng quan hệ tương đương, đặt \(X=I\times I\) và xác định \(\sim\) là quan hệ tương đương mà \((x,0)\sim (x,1)\). Khi đó \(X/\sim\) sẽ đồng phôi với một cái ống \(S^{1}\times I\). Hơn nữa, nếu $\sim$ thỏa mãn $(1,y)\sim (0,y)$ thì $X/\sim$ sẽ đồng phôi với một hình xuyến (torus) $S^{1}\times S^{1}$.
Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 25-06-2021 - 01:50