Mình thấy có một chứng minh Tiên đề Euclid nhờ mọi người xem và chỉ cho mình thấy lỗi sai trong chứng minh này với:
ĐỊNH LÍ EUCLID
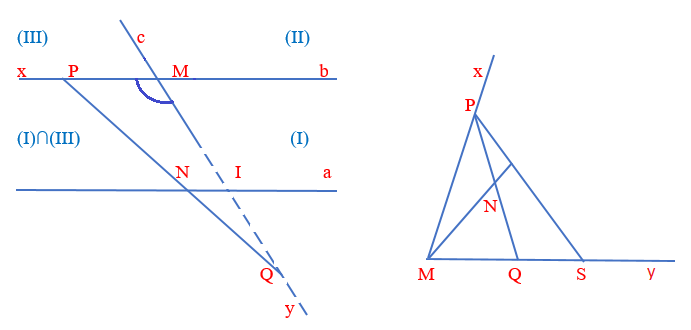
Định lí Euclid: Cho điểm M ở ngoài đường thẳng a. Đường thẳng đi qua M và song song với a là duy nhất (Tiên đề Euclid)
Chứng minh:
Giả sử qua M có hai đường thẳng b và c cùng song song với a.
Đường thẳng b chia mặt phẳng thành 2 phần là nửa mặt phẳng (I) và nửa mặt phẳng (II). Vì b//a nên đường thẳng a phải nằm trong một nửa mặt phẳng nào đó có bờ là b. Giả sử a ⸦ nmp (I) .Tương tự c chia mặt phẳng thành 2 phần là nửa mặt phẳng (III) và nửa mặt phẳng (IV) do c//a nên a ⸦ nmp (III)
Vậy đường thẳng a phải nằm trong phần chung của hai nửa mặt phẳng (I) và (III)
Từ đó a nằm trong góc xMy với Mx ⸦ b, My ⸦ c do hai đường thẳng b,c cắt nhau tại M tạo ra. (xMy = nmp(I)∩nmp(III)
Lấy một điểm N bất kì thuộc a. Do a nằm trong góc xMy nên điểm N cũng nằm trong góc xMy. Khi đó rõ ràng điểm N sẽ nằm trên một miền nào đó của góc xMy. Do đó phải có một miền tam giác MPS nào đó của góc xMy chứa điểm N với P nằm trên Mx, S nằm trên My và P ≠ M ≠ S.
Với điểm N nằm trong miền tam giác MPS ( với P ϵ Mx, S ϵ My, P ≠ M ≠ S ) của góc xMy khi đó N sẽ nằm trong góc MPS nên tia PN sẽ nằm giữa hai tia PM và PS do đó tia PN sẽ cắt đoạn thẳng MS tại Q nằm giữa M và S. Lúc này ta có N nằm giữa P và Q (vì tia MN nằm giữa hai tia MP và MQ) với P ϵ Mx, Q ϵ My, P ≠ M ≠ Q.
Đường thẳng a đi qua điểm N nằm giữa P và Q (chú ý đường thẳng PQ ≠ a) nên P và Q sẽ nằm trên hai nửa mặt phẳng đối nhau có chung bờ a. Hay P nằm tronq nửa mặt phẳng đối của nửa mặt phẳng bờ a chứa Q
P ϵ Mx ⸦ b → P ϵ b và M ϵ b nên P, M và b cùng thuộc một nửa mặt phẳng bờ a do đó P, M, b cùng nằm tronq nửa mặt phẳng đối của nửa mặt phẳng bờ a chứa Q.
Vì M và Q nằm trên hai nửa mặt phẳng đối nhau có chung bờ a. Nên đường thẳng MQ sẽ luôn cắt a tại một điểm I nào đó.
Do M ϵ c, Q ϵ c (vì Q ϵ My ⸦ c) nên c ≡ MQ hay ta có c cắt a tại I dẫn đến mâu thuẫn với c//a. Vậy điều giả sử là không đúng. Có nghĩa là qua M không thể có hai đường thẳng b và c cùng song song với a. Hay nói cách khác chỉ có một đường thẳng đi qua M và song song với a.
Định lí Euclid đã được chứng minh.□