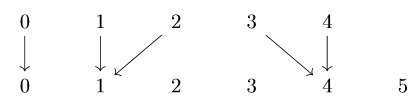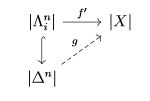Chủ đề này có 7 trả lời

[bangbang1412]

Bài viết giới thiệu về lý thuyết đơn hình (simplicial theory), một lý thuyết "tổ hợp" của tôpô đại số. Kí hiệu $\mathbf{Top},\mathbf{Sets},\mathbf{Ab}$ lần lượt là phạm trù các không gian tôpô, phạm trù các tâp hợp, phạm trù các nhóm abel.

 

Giới thiệu

H. Poincaré lần đầu định nghĩa đồng điều theo nghĩa tam giác phân một không gian và thực hiện các tính toán tổ hợp với định nghĩa này. Tuy nhiên cách định nghĩa này không hiệu quả ở điểm nó cần chứng minh các cách tam giác phân đều cho ta một nhóm đồng điều.

 simplex.png   69.18K   92 Số lần tải

Tiếp đó, không phải mọi không gian đều có thể tam giác phân. Sau này, các định nghĩa trừu tượng cho phép ta hiểu một tam giác là một ánh xạ liên tục $\left |\Delta^n \right| \to X$, trong đó $\left |\Delta^n \right|^n$ định nghĩa bởi

\begin{equation} \left|\Delta^n \right|=\left \{ (x_0,...,x_n) \in \mathbb{R}^{n+1} \mid x_i \in [0,1], x_0 + \cdots + x_n = 1 \right \}.\end{equation}

Các ánh xạ này cho ta một họ
\begin{equation} \mathrm{Sing}(X)_n = \left \{ \sigma: \left|\Delta^n \right| \to X \mid \sigma \ \text{liên tục} \ \right\}. \end{equation}
Tuy nhiên các tập $\mathrm{Sing}(X)_n$ không đứng riêng lẻ do bản thân các đơn hình hình học $\left|\Delta^n \right|$ có liên hệ với nhau, ví dụ một tam giác sẽ có ba đỉnh. Ngoài ra, do tính affine ta hoàn toàn có thể đồng nhất các đơn hình hình học với các đỉnh của nó. Ví dụ $\left|\Delta^n \right|$ có $(n+1)$-đỉnh $v_0,...,v_n$ ($v_i$ có tất cả các vị trí là $0$ ngoài $1$ ở vị trí $i$) có thể đồng nhất với tập $\left \{0,1,...,n \right \}$. Như vậy một tam giác có thể xem là "tập" $\left \{0,1,2\right \}$ với ba đỉnh $\left \{0 \right \}, \left \{1\right \}, \left \{2 \right \}$ và ba cạnh $\left \{0,1\right \}, \left \{1,2\right \}, \left \{0,2\right \}$. Đây là sự xuất hiện của phạm trù $\Delta$ với vật là các tập $[n]=\left \{0,1,...,n \right \}$, nó được gọi là phạm trù số. Trong khi $\mathrm{Sing}(X)$ là một tập đơn hình theo nghĩa nó gửi mỗi $[n]$ đến $\mathrm{Sing}(X)_n$ (nó cũng là một $\infty$-phạm trù). Như vậy, tóm gọn lại ta có một quy trình
\begin{equation} X  \rightarrow (\text{phức kì dị}) \ \mathrm{Sing}(X) \rightarrow (\text{hàm tử tự do}) \ \mathbb{Z}\mathrm{Sing}(X) \rightarrow (\text{phức+ đồng điều}) \  H_{\bullet}(X).\end{equation}
Thực chất đây là một loạt các hàm tử giữa các phạm trù
\begin{equation} \mathbf{Top} \to s\mathbf{Sets} \to s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab}),\end{equation}
trong đó $s\mathbf{Sets},s\mathbf{Ab}$ lần lượt là phạm trù các tập đơn hình và phạm trù các nhóm abel đơn hình. Như vậy thực chất ta đang làm đại số đồng điều trong $\mathbf{Ch}_{\geq 0}(\mathbf{Ab})$. Sau này ta sẽ biết rằng  $\mathrm{Sing}: \mathbf{Top} \to s\mathbf{Sets}$ có liên hợp là hàm tử hình học hóa trong khi đó định lý tương ứng Dold-Kan nói rằng $s\mathbf{Ab}$ tương đương với $\mathbf{Ch}_{\geq 0}(\mathbf{Ab})$, như vậy bước khó khăn có lẽ nằm ở phép lấy hàm tử nhóm abel tự do.

 

Định lý tương ứng Dold-Kan là một tương đương giữa hai phạm trù các phức không âm và các vật đơn hình. Để hiểu định lý Dold-Kan do đó ta bắt buộc phải hiểu các vật đơn hình, và để hiểu các vật đơn hình ta phải hiểu phạm trù $\Delta$. Để định nghĩa phạm trù số ta sẽ định nghĩa các đối mặt và đối suy biến (ta gọi như vậy để thuận tiện thay vì gọi là phép đối mặt và phép đối suy biến). Sau đó chúng ta chứng minh các đẳng thức đối đơn hình và chứng minh mọi cấu xạ trong phạm trù số có một phân tích rất đặc biệt gọi là phân tích đơn-toàn cấu.

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 17-10-2021 - 18:25

[bangbang1412]

Phạm trù số

 

Định nghĩa 1. $\Delta$ là phạm trù mà các vật là các tập sắp thứ tự toàn phần $[n] = (0 \leq 1 \leq ... \leq n)$, các cấu xạ là các ánh xạ bảo toàn thứ tự $\alpha: [m] \to [n]$, điều này có nghĩa $\alpha(i) \leq \alpha(j)$ nếu $i \leq j$.  Một đơn cấu (tương ứng, toàn cấu) trong $\Delta$ được định là ánh xạ bảo toàn thứ tự và là đơn ánh trên tập hợp (tương ứng, toàn ánh).

 

Định nghĩa 2. Đối mặt là các cấu xạ $d^i: [n-1] \to [n]$, $0 \leq i \leq n$ cho bởi
\begin{equation}
    d^i(k) = \begin{cases}
        k, & k < i\\
        k+1, & k \geq i+1
    \end{cases}
\end{equation}
Về ý nghĩa, các cấu xạ $d^i$ là các đơn cấu duy nhất $[n-1] \to [n]$, nó khuyết phần tử $i \in [n]$. Các cấu xạ $s^i: [n+1] \to [n], 0 \leq i \leq n$ cho bởi
\begin{equation}
    s^i(k) = \begin{cases}
        k, & k < i \\
        k-1, & k \geq i+1
    \end{cases}
\end{equation}
là các toàn cấu duy nhất $[n+1] \to [n]$, chúng được gọi là các đối suy biến. $s^i$ lặp phần tử $i \in [n]$ hai lần.

 

Định lý 3. Mọi cấu xạ $\alpha: [m] \to [n]$ có thể viết thành hợp một số đối mặt và một số đối suy biến.

 

Chứng minh. Ta chứng minh bằng quy nạp theo $n$. Nếu $n=0$ thì $\alpha$ hoặc là ánh xạ đồng nhất hoặc là hợp một số đối mặt. Giả sử khẳng định đúng tới $n$ và $\alpha: [n+1] \to [m]$ là một cấu xạ. Nếu $\alpha$ là đơn cấu thì $\alpha$ là hợp một số đối mặt. Nếu $\alpha$ không là đơn cấu thì tồn tại $k \in [n+1]$ mà $\alpha(k) = \alpha(k+1)$ (lưu ý điều này không xảy ra với một ánh xạ tổng quát mà chỉ đúng khi $\alpha$ bảo toàn thứ tự). Xét cấu xạ $\alpha':[n] \to [m]$ xác định bởi $\alpha'(i) = \alpha(i)$ nếu $i \leq k$ và $\alpha'(i) = \alpha(i+1)$ nếu $i>k$. Khi đó $\alpha = \alpha' s^k$ và ta thu được điều phải chứng minh khi áp dụng giả thiết quy nạp cho $\alpha'$.

 

Từ định lý trên ta thấy chỉ nên hạn chế sự tập trung xuống các đối mặt và các đối suy biến. Cụ thể, ta có một loạt các đẳng thức liên hệ trong định lý dưới đây.

 

Bổ đề 4. Trong phạm trù số các đẳng thức sau, gọi là các đẳng thức đối đơn hình, thỏa mãn

\begin{matrix}
       d^j d^i = d^i d^{j - 1}  & i < j \\
       s^j d^i = d^i s^{j-1}  &  i < j\\
       s^j d^j = \mathrm{id} = s^j d^{j+1} & \\
       s^j d^i = d^{i-1} s^j & i > j+1 \\
       s^j s^i = s^i s^{j+1} & i \leq j \\
\end{matrix}

Chứng minh. Ta chỉ chứng minh đẳng thức đầu tiên, tất cả các đẳng thức còn lại chứng minh tương tự. Lấy $i < j$ và $k \in [n]$. Ta có
\begin{equation}
    d^j d^i(k) = d^j\left(\begin{cases} k, & k < i \\ k + 1, & k \geq i \end{cases} \right) =
    \begin{cases}
        k, & k < i\\
        k+1,& i \leq k, k+1 < j \\
        k+2, &j \leq k+1
    \end{cases}
\end{equation}
và
\begin{equation}
    d^i d^{j-1}(k) = d^i\left(\begin{cases} k, & k < j -1 \\ k+ 1, & k \geq j-1 \end{cases} \right) = \begin{cases}
        k, & k < i \\
        k+1, & i \leq k, k+1 < j \\
        k+2, & j \leq k+1
    \end{cases}
\end{equation}
Do đó $d^j d^i = d^i d^{j-1}$ nếu $i < j$.

 

Định lý 5 (phân tích đơn-toàn cấu). Với mọi ánh xạ bảo toàn thứ tự $\varphi: [n] \to [m]$, tồn tại và duy nhất một phân tích $\varphi = \mu \sigma$ trong đó $\mu, \sigma$ lần lượt là các toàn cấu, đơn cấu bảo toàn thứ tự.

 

Chứng minh. Trước tiên ta chứng minh sự tồn tại, gọi $i_s <...<i_1$ là các phần tử của $[m]$ không nằm trong ảnh của $\varphi$ và $j_1 < ... <j_t$ là các phần tử của $[n]$ mà $\alpha(j) = \alpha(j+1)$. Nếu $p = n-t = m-s$ thì ta có một phân tích
\begin{equation}
    [n] \overset{\sigma}{\twoheadrightarrow} [p] \overset{\mu}{\hookrightarrow} [m]
\end{equation}
trong đó $\mu=d^{i_1}...d^{i_s}$ và $\sigma = s^{j_1}...s^{j_t}$. Để minh hoạ cho chứng minh, ta xét một cấu xạ $[4] \to [5]$ được cho bởi hình sau

 1.png   4.16K   70 Số lần tải

Như vậy tập ảnh của cấu xạ này là $(0<1<4)$, ta nhúng $(0<1<2)$ vào $[5]$ bởi $0\mapsto 0, 1 \mapsto 1, 2 \mapsto 4$ sẽ thu được phân tích  

 2.png   5.04K   51 Số lần tải

Dễ thấy $[4] \twoheadrightarrow [2]$ và $[2] \hookrightarrow [5]$.

Bây giờ ta chứng minh tính duy nhất, lấy hai đơn cấu $\mu_i:[k_1] \to [m]$ và hai toàn cấu $\sigma:[n] \to [k_i]$ ($i = 1,2$) thỏa mãn $\varphi = \mu_1\sigma_1 = \mu_2\sigma_2$. Đếm số lượng phần tử của ảnh $\mathrm{Im}(\mu_i \sigma_i)$ ta suy ra $k_1=k_2$ và do $\mu_1,\mu_2$ là các đơn cấu với cùng tập ảnh ta suy ra $\mu_1=\mu_2=\mu$, điều này cũng suy ra $\sigma_1=\sigma_2$ do $\mu$ là đơn cấu.

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 17-10-2021 - 18:12

[bangbang1412]

Lý thuyết đồng luân trong phạm trù vật đơn hình

 

Định nghĩa 6. Một vật đơn hình trong một phạm trù $\mathscr{C}$ là một hàm tử $X: \Delta^{op} \to \mathscr{C}$. Phạm trù $s\mathscr{C}=\mathscr{C}^{\Delta^{op}}=\mathrm{Fun}(\Delta^{op},\mathscr{C})$ có vật là các vật đơn hình và cấu xạ là các biến đối tự nhiên giữa chúng. Hơn nữa ta viết, $X_n = X([n]), d_i = X(d^i)$ là mặt và $s_j = X(s^j)$ là suy biến của $X$. Nếu $\alpha$ là một cấu xạ trong $\Delta$, ta viết $X(\alpha) = X_{\alpha}$.

 

Ví dụ 7. Một tập đơn hình trong phạm trù tập hợp $\mathbf{Sets}$ được gọi là một tập đơn hình, một trong các tập đơn hình thú vị nhất là $\Delta^n= \mathrm{Hom}_{\Delta}(\square,[n]): \Delta^{op} \to \mathbf{Sets}$ - ta gọi đây là đơn hình chuẩn $n$-chiều. Theo bổ đề Yoneda ta có
\begin{equation}
    X_n = X([n]) \cong \mathrm{Hom}(\mathrm{Hom}(\square,[n]),X).
\end{equation}
Phép nhúng Yoneda
\begin{equation}
    \begin{split}
        \Delta &\hookrightarrow \mathbf{Sets}^{\Delta^{op}} \\
        [n] & \mapsto \Delta^n
    \end{split}
\end{equation}
là trung thành, đầy đủ, hơn nữa nó còn trù mật theo nghĩa nếu $\mathscr{C}$ là một phạm trù có đối giới hạn với tập chỉ số bất kỳ thì mọi hàm tử $u:\Delta \to \mathscr{C}$ đều có thể nâng lên thành một hàm tử $u_{!}:\mathbf{Sets}^{\Delta^{op}} \to \mathscr{C}$. Nói cách khác, ta có một biểu đồ giao hoán

 3.png   1.86K   72 Số lần tải

Cụ thể với mỗi $X \in \mathrm{Obj}(\mathbf{Sets}^{\Delta^{op}})$ thì theo ta biết $X \cong \underset{\Delta^n \to X}{\mathrm{colim}} \ \Delta^n$ (chứng minh sau!) nên ta có thể định nghĩa
\begin{equation}
    u_{!}(X) = \underset{\Delta^n \to X}{\mathrm{colim}} \ u([n]).
\end{equation}
Ngược lại ta cũng có một hàm tử $u^{\star}: \mathscr{C} \to \mathbf{Sets}^{\Delta^{op}}$ là liên hợp của $u_{!}$ định nghĩa bởi
\begin{equation}
    (u^{\star}(C))_n = \mathrm{Hom}_{\mathscr{C}}(u([n]),C) \ \forall \ C \in \mathrm{Obj}(\mathscr{C}).
\end{equation}

Về sau ta sẽ thấy cặp liên hợp $(\mathrm{Sing}(\square),\left | \square \right|)$ là một hệ quả của ý tưởng vừa phân tích.

 

Bổ đề 8. Với mọi vật đơn hình $X$ thì các đẳng thức sau, gọi là các đẳng thức đơn hình, thỏa mãn

\begin{matrix}
      d_i d_j = d_{j-1} d_i & i < j\\
       d_i s_j= s_{j-1}d_i &  i < j\\
       d_j s_j = \mathrm{id} = d_{j+1}s_j & \\
       d_i s_j =  s_j d_{i-1} & i > j+1 \\
       s_i s_j = s_{j+1}s_i & i \leq j
\end{matrix}

 

Chứng minh. Hệ quả hiển nhiên của các đẳng thức đối đơn hình.

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 30-01-2023 - 19:58

[bangbang1412]

Hàm tử phức chuẩn hóa và phần suy biến

 

Bắt chước cách làm của phức kì dị của một không gian tôpô ta định nghĩa khái niệm phức Moore.

 

Định nghĩa 9. Phức Moore $M$ là một hàm tử $M: s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ biến mỗi vật đơn hình $A$ thành một phức (cùng kí hiệu) $A$ mà vị trí thứ $n$ là $A_n$ và vi phân

$$d = d_0 - d_1 + ... + (-1)^n d_n: A_n \to A_{n-1}.$$

Một thủ tục đơn giản cho ta thấy $d^2=0$. 

 

Câu hỏi. $M: s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ có phải là một phần trong tương đương ta mong muốn không?

 

Trả lời. Không. Cụ thể hơn, nếu $M$ là một phần của tương đương, thì nó phải toàn ánh trên lớp các vật, nói riêng, phải tồn tại một vật đơn hình $A$ mà $MA$ là phức

$$ ... \to 0 \to 0 \to \mathbb{Z} (\text{vị trí 0}) \to 0.$$

Do đó $A_0 = \mathbb{Z},A_1 = 0$, tuy nhiên nhắc lại rằng $s_j$ là đơn cấu nên $A_0 \hookrightarrow A_1$, điều này vô lý. 

 

Lý do xảy ra điều này là vi phân của phức Moore quá phức tạp và quá dư thông tin trong từng thành phần $A_n$, ta sẽ thu nhỏ $M$ để đạt được tương đương mong muốn. 

 

Định nghĩa 10. Hàm tử phức chuẩn hóa $N: s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ biến mỗi vật đơn hình $A$ thành phức $N$ mà

$$(NA)_n = \bigcap_{i=1}^n \mathrm{Ker}(d_i:A_n \to A_{n-1}) \ \forall n > 0, \ (NA)_0 = A_0.$$

Dễ thấy $(NA)_{\bullet}$ là một phức với vi phân $d_0$ (do trong vi phân $d$ của phức Moore triệt tiêu hết $d_1,...,d_n$). Đồng điều của phức chuẩn hóa được gọi là nhóm đồng luân của vật đơn hình, kí hiệu

$$\pi_n(A) = H_n(NA).$$

 

Ví dụ 11. $N\mathbb{Z}\Delta[0]$ chính là phức $ ... \to 0 \to 0 \to \mathbb{Z} (\text{vị trí 0}) \to 0$, do đó khẳng định phức chuẩn hóa là tốt hơn phức Moore. 

 

Chúng ta trước tiên sẽ chứng minh hai tính chất của hàm tử phức chuẩn hóa: nó loại bỏ tất cả phần "suy biến" trong một vật đơn hình, nó là hàm tử trung thành, đầy đủ. 

 

Định nghĩa 12. Phần suy biến được định nghĩa bởi $(DA)_n = \sum_{i=0}^n s_i(X_{n-1})$. 

 

Bổ đề 13. $(NA)_n \cap (DA)_n = 0$. 

 

Chứng minh. Lấy $x \in (NA)_n \cap (DA)_n$, khi đó tồn tại số $i$ lớn nhất mà 

$$x = s_i(a_i) + \cdots + s_n(a_n), \ a_j \in X_{n-1}.$$

Nếu $i = n$ thì $0 = d_n x = d_n s_n (a_n) = 0 \Rightarrow x = s_n(a_n) = 0$. Trong trường hợp $i \leq n-1$ ta tác động $d_i$ vào hai vế thu được

\begin{align*} 0  = d_i x & = a_i + d_i s_{i+1}(a_{i+1}) \cdots + d_i s_n (a_n) \\ & = a_i + s_i d_i(a_{i+1}) + \cdots + s_{n-1}d_i(a_n). \end{align*} Hệ quả là 

\begin{align*} x & = s_i\left(s_i d_i(-a_{i+1})  + \cdots + s_{n-1}d_i(a_n) \right) + s_{i+1}(a_{i+1}) + \cdots + d_i s_n(a_n) \\ & = s_{i+1}s_id_i(-a_{i+1}) + \cdots s_n s_i d_i(a_n) + s_{i+1}(a_{i+1}) + \cdots + s_n(a_n) \\ & = s_{i+1}(a_{i+1}-s_id_i(a_{i+1})) + ... + s_n(a_n - s_i d_i(a_n)), \end{align*} điều này trái với giả thuyết về $i$.

 

Bổ đề 14. $(NA)_n + (DA)_n = A_n$. 

 

Chứng minh. Đặt các nhóm con $P_n^k = \left \{x \in A_n \mid d_i x = 0 \ \forall i > k \right \}$ 

$$(NA)_n = P^0_n \subset P^1_n \subset ... \subset P^n_n = A_n.$$

Ta sẽ chứng minh bằng quy nạp rằng $P^i_n + D_n = A_n$ bằng quy nạp lùi. Khi $i=n$ thì hiển nhiên, giả sử khẳng định đúng với $i=k$, ta chứng minh nó đúng với $i=k-1$. Lấy $a \in A_n$ ta giả sử viết được $a = b + c$ với $b \in P^k_n, c \in D_n$, khi đó có thể kiểm tra

$$a = (b - s_{k-1}d_kb) + (c + s_{k-1}d_k b)$$ trong đó có thể kiểm tra $b-s_{k-1}d_k b \in P^{k-1}_n$ và $c + s_{k-1}d_k b \in D_n$. 

 

Bổ đề 15. Đồng luân của một nhóm abel đơn hình đẳng cấu với đồng điều của chính nó 

$$\pi_n(A) \cong H_n(MA).$$

Chứng minh. Ta chỉ cần chứng minh $D=DA$ là acyclic. Ta lọc $DA$ bởi

$$F_i D_n  = \begin{cases} 0 & i = 0, \\ D_n & n \leq p, \\ s_0(A_{n-1}) + \cdots + s_p(A_{n-1}) &  \text{trường hợp khác}. \end{cases}$$ Hiển nhiên lọc này bị chặn nên ta có một dãy phổ

$$ E^1_{p,q} = H_{p+q}(F_pD/F_{p-1}D) \Rightarrow_{p+q=n} H_{p+q}(D).$$

Hệ quả là ta cũng chỉ cần chứng minh $F_pD/F_{p-1}D$ là một phức acyclic, ta có thể xây dựng một toán tử đồng luân tầm thường $\sigma: (F_pD/F_{p-1}D)_n \to (F_pD/F_{p-1}D)_{n+1}$ thỏa mãn

$$\mathrm{id} = \sigma \left( \sum (-1)^i d_i \right) + \left(\sum (-1)^i d_i \right) \sigma.$$

Cụ thể ta tìm được $\sigma_n = (-1)^{p+1}s_p$. Đây chỉ là kiểm tra trực tiếp với các đẳng thức đơn hình, lưu ý mỗi phần tử của

$$(F_pD/F_{p-1}D)_n = \frac{s_0(A_{n-1}) + \cdots + s_{p-1}(A_{n-1}) + s_p(A_{n-1})}{s_0(A_{n-1}) + \cdots + s_{p-1}(A_{n-1})}$$ đều có dạng $s_p(\text{smth})$.

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 17-10-2021 - 18:13

[bangbang1412]

Tương ứng Dold-Kan

 

Sau đây ta sẽ phát biểu một phần của tương ứng Dold-Kan. 

 

Định lý 16(Dold-Kan). Hàm tử phức chuẩn hóa $N: s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ là một hàm tử đầy đủ, trung thành, nói cách khác,

$$N: \mathrm{Hom}_{s\mathbf{Ab}}(A,B) \cong \mathrm{Hom}_{\mathbf{Ch}_{\geq0}}(NA,NB) \ \forall \ A,B \in s\mathbf{Ab}. $$

Để chứng minh nó ta cần bổ đề sau. 

 

Bổ đề 17. Với mọi $a \in A_n$ ta có một phân tích (duy nhất, tuy nhiên ta chỉ chứng minh sự tồn tại) dạng 

$$x = \sum_{\beta} A(\beta)(x_{\beta}),$$

trong đó $x_{\beta} \in (NA)_p$ và $\beta: [n] \twoheadrightarrow [p]$. 

 

Chứng minh. Nhắc lại rằng $a = b+ \sum_{i=0}^n s_i(a_i)$ với $b \in (NA)_n, a_i \in A_{n-1}$. Theo giả thiết quy nạp $a_i = \sum A(\beta')(x_{\beta'})$ với $\beta:[n-1] \twoheadrightarrow [p]$ và nhắc lại từ phân tích đơn-toàn cấu mỗi toàn cấu $[n] \twoheadrightarrow [p]$ được phân tích thành $[n] \to [n-1] \to [p]$ với $[n-1] \to [p]$ là một đối suy biến. 

 

Chứng minh định lý Dold-Kan. Trước tiên ta chứng minh $N$ là đơn cấu, giả sử $f: A \to B$ là một cấu xạ giữa hai nhóm abel đơn hình với $N(f) = 0$. Với $a \in A_n$ ta viết $a = \sum A(\beta)(x_{\beta})$, do đó 

\begin{align*} f(x) & = f\left( \sum A(\beta)(x_{\beta}) \right) \\ & = \sum f\left(A(\beta)(x_{\beta})\right) \\ & = \sum B(\beta)(f(x_{\beta})) \\ & = \sum B(\beta)(N(f)(x_{\beta})) = 0. \end{align*} Tiếp theo ta chứng minh $N$ là toàn cấu, lấy $g: NA \to NB$, ta đặt $f: A \to B$ trong đó

$$f(x) = \sum B(\beta)(x_{\beta}),$$

với $x = \sum A(\beta)(x_{\beta})$. Dễ kiểm tra $Nf = g$. 

 

Giờ ta sẽ tìm nghịch đảo của $N$ là một hàm tử $K: \mathbf{Ch}_{\geq 0}(\mathbf{Ab}) \to s\mathbf{Ab}$.

 

Định nghĩa 18. Định nghĩa hàm tử $K$ bởi $KC = \mathrm{Hom}_{\mathbf{Ch}_{\geq 0}}(N\mathbb{Z}\Delta[\square],C)$. 

 

Mệnh đề 19. Ta có một đẳng cấu $A \cong (KNA)$ với mọi nhóm abel đơn hình $A$. 

 

Chứng minh. Điều này suy ta từ định nghĩa

$$A_n \cong \mathrm{Hom}(\mathbb{Z}\Delta[n],A) \cong \mathrm{Hom}(N\mathbb{Z}\Delta[n],NA) = (KNA)_n.$$

Trước khi đi tiếp ta cần một bổ đề kĩ thuật, ta sẽ không chứng minh. 

 

Bổ đề 20. Với mỗi $n$ thì $(N\mathbb{Z}\Delta[n])_m$ là nhóm abel tự do với cơ sở là các đơn ánh $[m] \hookrightarrow [n]$. Bên cạnh đó với mỗi cấu xạ dây chuyền $f: N\mathbb{Z}\Delta[n] \to C$ thì $f \in D_n(KC)$ khi và chỉ khi $f_r = 0 \ \forall r \geq n$. 

Về khẳng định thứ hai của bổ đề ta có thể hiểu nôm na nếu như $f = \sum_{i=0}^n s_i(f_i)$ với $f_i: N\mathbb{Z}\Delta[n-1] \to C$, tuy nhiên $N\mathbb{Z}\Delta[n-1])_r = 0$ do không có đơn cấu nào $[r] \hookrightarrow [n-1]$.

 

Mệnh đề 21. Với mỗi $n$ ta có một đẳng cấu $\phi_n: (NKC)_n \to C_n, f \mapsto f_n(\mathrm{id}_{[n]})$; họ đẳng cấu này cho ta một đẳng cấu giữa hai phức $NKC \cong C$. 

 

Phác thảo chứng minh. Trước hết ta cần xem $NKC$ "trông" như thế nào

$$(NKC)_n = \bigcap_{i=1}^n \mathrm{Ker}\left(d_i: \mathrm{Hom}(N\mathbb{Z}\Delta[n],C) \to \mathrm{Hom}(N\mathbb{Z}\Delta[n-1],C) \right).$$

Như vậy nếu $f \in (NKC)_n$ thì $d_i(f) = f \circ d^i = 0$ với mọi $i>0$. Bây giờ ta chứng minh tính đơn ánh, giả sử $f \in \mathrm{Ker}(\phi_n)$ thì hiển nhiên $f_r = 0 \ \forall r > n$ và $f_n(\mathrm{id}_{[n]})=0$ suy ra $f_n = 0$. Theo bổ đề trước thì $f \in D_n(KC)$, tuy nhiên $f \in N_n(KC)$ nên $f = 0$ theo bổ đề $N \cap D = 0$.

 

Về tính toàn ánh, với mỗi $x \in C_n$ ta xét $g$ thỏa mãn $g_r \equiv 0$ với mọi $r \neq n,n-1$; $g_n(\mathrm{id}_{[n]}) = x$ và 

$$g_{n-1}(d^i) =  \begin{cases} \partial(x) & i = 0, \\ 0 & i > 0 \end{cases}$$

Khi đó dễ kiểm tra $\phi_n(g) = x$. 

 

Định lý tương ứng Dold-Kan đầy đủ. Hai hàm tử $(N,K)$ là một cặp tương đương. Hơn thế nữa, tương đương này còn bảo toàn đồng luân theo nghĩa chặt, nói như vậy có nghĩa trong cả hai phạm trù $s\mathbf{Ab},\mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ đều có các quan hệ đồng luân và chúng được bảo toàn hoàn toàn qua $N,K$ theo nghĩa: đồng luân trong phạm trù này khi và chỉ khi đồng luân trong phạm trù kia sau khi áp dụng hàm tử.

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 17-10-2021 - 18:14

[bangbang1412]

Lý thuyết đồng luân đơn hình: không gian Eilenberg-MacLane, không gian Moore

 

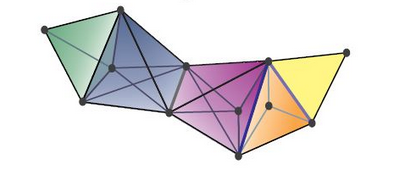
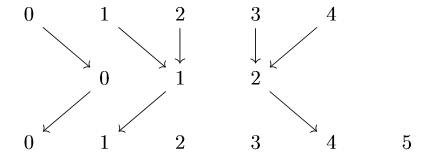
Định nghĩa 22. Với mọi $n$ và $0 \leq i \leq n$, $(n,i)$-sừng (tiếng Anh, horn) $\Lambda^n_i:\Delta^{op} \to \mathbf{Sets}$ là tập đơn hình con của $\Delta^n$ định nghĩa bởi
$$(\Lambda_i^n)([m]) = \left \{\alpha \in \mathrm{Hom}_{\Delta}([m],[n]) \mid [n] \not\subset \alpha([m]) \cup \left \{i \right \} \right \}.$$ Một cách hình học, $\Lambda^n_i$ chính là hợp của tất cả các mặt ngoại trừ mặt thứ $i$ của $\Delta^n$.

 

Định nghĩa 23. Cho $X$ là một tập đơn hình, khi đó $X$ được gọi là fibrant nếu nó thỏa mãn điều kiện Kan sau:

Với mỗi cấu xạ $f: \Lambda_i^n \to X$, tồn tại $\overline{f}: \Delta^n \to X$ làm giao hoán biểu đồ sau

 Screenshot 2021-10-16 at 02-27-54 Phạm Khoa Bằng_K62CNKHTN_Hội đồng Đại số-Hình học-Tôpô.png   1.76K   27 Số lần tải

Ở ngôn ngữ tập hợp nó có nghĩa là:

Với mọi $n$ và $k$ thỏa mãn $0 \leq k \leq n$, nếu $x_0,...,x_{k-1},x_{k+1},...,x_n \in X_n$ thỏa mãn $d_i x_j = d_{j-1}x_i \ \forall i < j$ và $i,j \neq k$ thì tồn tại $y \in X_{n+1}$ sao cho $d_i(y) = x_i \ \forall i \neq k$.

 

Mặc dù không sử dụng định nghĩa này, nhưng ta vẫn nhắc lại rằng một $\infty$-phạm trù là một tập đơn hình $X$ thỏa mãn điều kiện Kan với mọi $\Lambda^n_i \to X$ với mọi $0 < i < n$, trong đó $n \geq 2$.

 

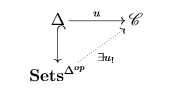
Định lý 24. Cho $\mathcal{F}:\mathscr{C} \to \mathbf{Sets}$ là một tiền bó của các tập hợp, khi đó $\mathcal{F}$ luôn có thể xem là một đối giới hạn trên một phạm trù slice.

 

Hệ quả 25. Cho $X$ là một tập đơn hình khi đó $X \cong \underset{\Delta^n \to X}{\mathrm{colim}}\ \Delta^n$, trong đó đối giới hạn được lấy trong phạm trù $(\Delta \downarrow X)$.

 

Định lý 26. Với mọi tập đơn hình $X$ thì $\left|X \right|$ luôn là một CW-phức.

 

Định lý 27. Hàm tử hình học hóa $\left| \square \right|: s\mathbf{Sets} \to \mathbf{Top}$ là liên hợp trái của hàm tử phức kỳ dị $\mathrm{Sing}(\square): \mathbf{Top} \to s\mathbf{Sets}$.

 

Chứng minh. \begin{equation*}
    \begin{aligned}
        \mathrm{Hom}_{\textbf{Top}}(\left | X \right|, Y) &  \cong \mathrm{Hom}_{\textbf{Top}}(\text{colim}_{\Delta^n \to X} \left |\Delta^n \right|, Y) \\
        & \cong \lim_{(\Delta \downarrow X)} \mathrm{Hom}_{\textbf{Top}}(\left |\Delta^n \right |, Y) \\
        & \cong \lim_{(\Delta \downarrow X)} \mathrm{Hom}_{\textbf{Sets}}(\Delta^n, \text{Sing}(Y)) \\
        & \cong \mathrm{Hom}_{\textbf{Sets}}(\text{colim}_{(\Delta \downarrow X)} \Delta^n, \mathrm{Sing}(Y))  \cong \mathrm{Hom}_{\textbf{Sets}}(X, \text{Sing}(Y))
\end{aligned}
\end{equation*}
với mọi tập đơn hình $X$ và không gian tôpô $Y$ nên ta có điều phải chứng minh.

 

Định lý 27. Cho $X$ là một không gian tôpô, khi đó vật đơn hình $\mathrm{Sing}(X)$ thỏa mãn điều kiện Kan.

 

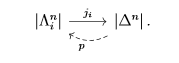
Chứng minh. Với mọi phép nhúng $j_i: \left| \Lambda_i^n \right| \hookrightarrow \left | \Delta^n \right|$ dễ thấy tồn tại một phép co rút $p: \left| \Delta^n \right| \to \left| \Lambda^n_i \right|$ theo nghĩa $p \circ j_i = \mathrm{id}$.

 Screenshot 2021-10-16 at 02-45-54 Phạm Khoa Bằng_K62CNKHTN_Hội đồng Đại số-Hình học-Tôpô.png   1.42K   26 Số lần tải

Ta đã định nghĩa dược hình học hóa của một tập đơn hình, một lẽ tự nhiên ta có thể định nghĩa $\pi_n(X) = \pi_n(\left|X \right|)$ với một tập đơn hình $X$. Dưới đây ta sẽ đưa ra một cách định nghĩa khác của nhóm đồng luân theo một cách hoàn toàn tổ hợp và nhóm định nghĩa được vẫn đẳng cấu với $\pi_n(\left|X\right|)$.

 Screenshot 2021-10-16 at 02-45-59 Phạm Khoa Bằng_K62CNKHTN_Hội đồng Đại số-Hình học-Tôpô.png   1.95K   26 Số lần tải

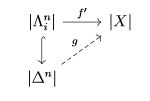
Tuy nhiên ta luôn có thể lấy $g = f' \circ p$.

 

Định nghĩa 28. Cho $X$ là một tập đơn hình và một điểm gốc $v \in X_0$, ta định nghĩa $\pi_n(X,v)$ như sau. Đặt
$$Z_n = \left \{ x \in X_n \mid d_i(x) = s_0^{n}(v) \forall i = \overline{0,n}  \right \}.$$ Ta nói hai phần tử $x, x'$ của $Z_n$ là đồng luân, kí hiệu $x \sim x'$, nếu tồn tại $y \in X_{n+1}$ (gọi là một đồng luân từ $x$ đến $x'$) thỏa mãn
$$d_i(y) = \begin{cases}
        s_0^{n}(v) ,&  i < n \\
        x, & i = n \\
        x,' &  i = n+1.
    \end{cases}$$

Bình luận. Trước tiên chi tiết lấy điểm gốc $v \in X_0$. Thứ nhất, ta có thể xem $X$ như một không gian tôpô và đồng thời là phức kì dị của nó $\mathrm{Sing}(X)$ khi đó một điểm gốc $v$ nên nằm trong $X = \mathrm{Sing}(X)_0$. Thứ hai, cách tạo ra điểm gốc này tạo cho ta một phạm trù mới $\mathbf{Top}_{\star}$ mà trong đó vật là các cặp $(X,v)$; khác với $\mathbf{Top}$, phạm trù này có vật $0$ là tập một phần tử. Tương tự, ta có phạm trù $s\mathbf{Sets}_{\star}$. Ta biết rằng cho $v \in X_0$ tương đương với cho
$$v \in \mathrm{Hom}_{s\mathbf{Sets}}(\Delta^0, X).$$ Một cách tự nhiên $v$ ta một phần tử trong $\mathrm{Hom}_{\mathbf{Sets}}((\Delta^0)_n,X_n)$ chính là $s^n_0(v) \in X_n$. Cuối cùng là định nghĩa của $Z_n$, ta nhắc lại định nghĩa nhóm đồng luân thông thường của một không gian tôpô $X$
$$\pi_n = \mathrm{Hom}_{\mathbf{Top}_{\star}}(S^n, X)/\simeq.$$ Theo quan điểm đơn hình, ta nên định nghĩa
$$\pi_n^{\text{đơn hình}} = \mathrm{Hom}_{s\mathbf{Sets}_{\star}}(\Delta^n/\partial \Delta^n, X)/\simeq,$$ trong đó $\partial \Delta^n = \cup d^i(\Delta^{n-1})$. Như vậy cho $\alpha \in  \mathrm{Hom}_{s\mathbf{Sets}_{\star}}(\Delta^n/\partial \Delta^n, X)$ tương đương với cho một $\alpha \in \mathrm{Hom}_{\mathbf{Sets}}(\Delta^n,X) \cong X_n$ mà

 Screenshot 2021-10-16 at 02-42-22 Phạm Khoa Bằng_K62CNKHTN_Hội đồng Đại số-Hình học-Tôpô.png   2.22K   26 Số lần tải

Nói cách khác, $s_0^{n}(v) = x(d^i) = d_i(x)$.

 

Bổ đề 29. Nếu $X$ là một tập đơn hình fibrant thì $\sim$ là một quan hệ tương đương.

 

Chứng minh. Quan hệ này là phản xạ do $y = s_n x$ là một đồng luân từ $x$ tới chính nó. Để thấy $\sim$ đối xứng và bắc cầu, gọi $y$ là một đồng luân từ $x$ tới $x'$ và $y'$ là một đồng luân từ $x'$ tới $x^{''}$. Điều kiện Kan áp dụng cho các phần tử $s_0^{n+1}(v),...,s_0^{n+1}(v),y,y'$ cho ta một phần tử $z \in X_{n+2}$ mà $d_{n}z = y, d_{n+1}z = y'$ và $d_iz = s_0^{n+1}(v)$ với $i < n$. Phần tử $d_{n+2}z$ do đó là một đồng luân tử $x$ đến $x^{''}$.

 

Định nghĩa 30. Cho $X$ là một tập đơn hình fibrant và một số nguyên $n \geq 1$, tập thương $Z_n/\sim$ có thể được trang bị một phép nhân khiến nó trở thành một nhóm, ta gọi đây là nhóm đồng luân của $X$, kí hiệu bởi $\pi_n(X,v)$.

 

Định lý 31. Nếu $X$ là một tập đơn hình fibrant thì cấu xạ chính tắc $\eta_X: X \to \mathrm{Sing}(\left| X \right|)$ là một đồng luân yếu. Hệ quả là $\eta_X$ cảm sinh một đẳng cấu chính tắc $\pi_n(X,x) \cong \pi_n(\left|X \right|,x)$ với mọi $n \geq 1$.

 

Định lý 32. Cho $X$ là một không gian tôpô thì cấu xạ chính tắc $j:\left| \mathrm{Sing}(X) \right| \to X$ là một đồng luân yếu. Ngoài ra nó cũng cảm sinh đẳng cấu trên tất cả các nhóm đồng điều.

 

Định nghĩa 33. Cho $X$ là một vật đơn hình trong $\mathscr{A}$, nhóm đồng luân thứ $n$ của $X$ định nghĩa bởi $\pi_n(X) = H_n(NX)$ trong đo $N$ là phức chuẩn hóa.

 

Ví dụ. Nếu $G$ là một nhóm đơn hình hoặc một môđun đơn hình với điểm gốc $v = 1$ (nhắc lại, $G$ luôn tự động là fibrant). Xét nhóm
$$N_n(G) = \left \{x \in G_n \mid d_i(x) = s_0^n(1) = 1 \ \forall \ i \neq 0 \right \}.$$ Khi đó $Z_n = \mathrm{Ker}(d_0:N_n \to N_{n-1})$ và $Z_n/\sim = Z_n/B_n$ trong đó $B_n = \left \{x \mid x \sim 1 \right\} = \mathrm{Im}(d_{n+1}:N_{n+1}\to N_n)$. Nói cách khác, $\pi_n(G,1)$ là đồng điều của phức $N_{\bullet}$
$$ ... \to N_2 \overset{d_2}{\rightarrow} N_1 \overset{d_1}{\rightarrow}N_0 \to 1.$$ Điều này giải thích tại sao định nghĩa trước là một mở rộng hợp lý.

 

Định nghĩa 34 (không gian Eilenberg-MacLane).

• Cho $G$ là một nhóm abel và $n$ là một số tự nhiên, một không gian tôpô $X$ thỏa mãn
  $$\pi_k(X)  = 0 \ \forall k \neq n, \
      \pi_n(X)  = G$$ được gọi là một không gian Eilenberg-MacLane kiểu $K(G,n)$.
• Cho $G$ là một nhóm abel và $n$ là một số tự nhiên, một tập đơn hình fibrant $K$ thỏa mãn
  $$ \pi_k(K)  = 0 \ \forall k \neq n, \
      \pi_n(K)  = G$$ được gọi là một tập đơn hình Eilenberg-MacLane kiểu $K(G,n)$.

Bổ đề 35. Cho $G$ là một nhóm abel và $n$ là một số tự nhiên, ta đồng nhất $G$ với phức $C_{\bullet}$ trong $\mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ mà $C_0 = G$ và $C_i = 0$ với mọi $i \neq 0$, khi đó $KG[-n]$ là một tập đơn hình Eilenberg-MacLane kiểu $K(G,n)$.

 

Chứng minh. Rõ ràng ta chỉ cần tính nhóm đồng luân của $KG[-n]$, tuy nhiên điều này khá dễ dàng vì theo định lý Dold-Kan thì $$\pi_k(KG[-n]) = H_k(NKG[-n]) \cong H_k(G[-n]) \cong G$$ nếu $k=n$ và $\cong 0$ nếu $k \neq n$.

 

Hệ quả. $\left|KG[-n] \right|$ là một không gian Eilenberg-MacLane kiểu $K(G,n)$.

 

Định nghĩa 36. Cho $X$ là một tập đơn hình fibrant, cấu xạ $h: X \to \mathbb{Z}X$ gửi $X$ tới các phần tử trong cơ sở của $\mathbb{Z}X$ cảm sinh một đồng cấu
$$\pi_{\bullet}(X) \to \pi_{\bullet}(\mathbb{Z}X) \cong H_{\bullet}(N\mathbb{Z}X) \cong H_{\bullet}(\mathbb{Z}X)$$ (ở đây ta đã sử dụng sự kiện phép chiếu $kX \to NX$ là một tương đương đồng luân), cấu xạ cảm sinh này được gọi là đồng cấu Hurewicz.

 

Định nghĩa 37. Cho một nhóm abel $G$ và một số nguyên $n \geq 1$, một không gian Moore kiểu $M(G,n)$ là một CW-phức $X$ thỏa mãn
$$\widetilde{H}_i(X)  = 0 \ \forall \ i \neq n, \ H_n(X)  = G,$$ trong đó $\widetilde{H}$ kí hiệu nhóm đồng điều rút gọn.

 

Bổ đề 38. Với mọi nhóm abel $G$ và một số nguyên $n \geq 1$, tồn tại một không gian Moore (không nhất thiết chính xác tới một đồng luân).

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 17-10-2021 - 18:19

[bangbang1412]

Định lý Dold-Thom

 

Trong phần này ta sẽ trình bày về tích đối xứng vô hạn, kết quả đáng lưu ý nhất trong phần này là định lý Dold-Thom nói rằng tích đối xứng vô hạn của không gian Moore chính là không gian Eilenberg-MacLane.

 

Định nghĩa 39. (Tích đối xứng vô hạn)

• Cho $X$ là một không gian tôpô với một điểm gốc $x_0 \in X$. Với mỗi $n \geq 0$ ta định nghĩa $$\mathrm{Sym}^0 X = x_0, \ \ \mathrm{Sym}^n X = X^n/ S_n \ \forall n \geq 1,$$ trong đó $X^n$ là tích Descartes $n$ lần của $X$, $X^n/S_n$ là không gian thương của $X^n$ dưới tác động của nhóm đối xứng $S_n$ bằng cách hoán đổi các vị trí. Các phép nhúng tự nhiên $\mathrm{Sym}^nX \to \mathrm{Sym}^{n+1}X$ định nghĩa bởi $(x_1,...,x_n) \mapsto (x_0,x_1,...,x_n)$. Tích đối xứng vô hạn $\mathrm{Sym}^{\infty}X$ được định nghĩa là giới hạn của dãy $$x_0 = \mathrm{Sym}^0 X \subset \mathrm{Sym}^1 X \subset \mathrm{Sym}^2X \subset ... \subset \mathrm{Sym}^nX \subset ...$$ tôpô trên $\mathrm{Sym}^{\infty}X$ được định nghĩa là tôpô yếu định nghĩa bởi họ $\left \{\mathrm{Sym}^n X \right \}$; tức là một tập $F \subset \mathrm{Sym}^{\infty}X$ là đóng khi và chỉ khi $F \cap \mathrm{Sym}^n X$ là đóng với mọi $n$.
• Cho $K$ là một tập đơn hình với một đỉnh góc $e_0 \in K_0$. Với mỗi $k > 0$ đặt $e_k = s_0^k e_0$ và định nghĩa $K(e_0)$ là vật đơn hình con của $K$ sinh bởi $e_0$ ($K(e_0)$ có đúng một $k$-đơn hình với mỗi $k \geq 0$, chính là $e_k$). Với mỗi $n \geq 0$, ta định nghĩa tích đối xứng $\mathrm{Sym}^n K$ bởi $$\mathrm{Sym}^0 K = K(e_0), \ \ \mathrm{Sym}^n K = K^n/S_n \ \forall n \geq 1,$$ trong đó $K^n$ là tích Descartes $n$ lần của $K$, $K^n/S_n$ là vật thương xác định bởi tác động của nhóm đối xứng bằng cách đổi chỗ các vị trí. Với mỗi $n \geq 1$, các $q$-đơn hình của $\mathrm{Sym}^nK$ là các bộ (không sắp thứ tự) $n$ vị trí, mỗi vị trí là một $q$-đơn hình của $K$, toán tử biên và suy biến thỏa mãn $$ d_i(\sigma_1...\sigma_n)  = (d_i \sigma_1)...(d_i\sigma_n), \ s_i(\sigma_1...\sigma_n)  = (s_i\sigma_1)...(s_i\sigma_n).$$ Ta định nghĩa một cấu xạ nhúng $\mathrm{Sym}^n K \to \mathrm{Sym}^{n+1}K, \sigma_1...\sigma_n \mapsto e_q \sigma_1...\sigma_q$ (nếu $\mathrm{dim}\sigma_i = q$) và gọi giới hạn của dãy $$K(e_0) = \mathrm{Sym}^0 K \subset \mathrm{Sym}^1 K \subset ... \subset \mathrm{Sym}^nK \subset ...$$ là tích đối xứng vô hạn của tập đơn hình $K$, kí hiệu $\mathrm{Sym}^{\infty}K$.

Sau đây, ta sẽ đi chứng minh $H_{\bullet}(\left|K \right|; G) \cong H_{\bullet}(\mathbb{Z}K;G)$ với mọi tập đơn hình $K$ và nhóm abel $G$. Nói riêng, $H_{\bullet}(\mathbb{Z}KG[-n]) \cong H_{\bullet}(K(G,n);\mathbb{Z})$.

 

Bổ đề 40. Nếu $f: (X, x_0) \to (Y,y_0)$ là một tương đương đồng luân thì $\mathrm{Sym}^nf$ cũng là một tương đương đồng luân với $n=0,1,...,\infty$.

 

Định lý 41. Với mọi tập đơn hình $K$ tồn tại một đồng luân yếu tự nhiên $$\left|\mathrm{Sym}^n K \right | \to \mathrm{Sym}^n \left|K \right|, \ \text{với} \ n = 0,1,...\infty.$$

 

Hệ quả 42. Cho $X$ là một CW-phức. Tồn tại một đồng luân yếu tự nhiên $\left|\mathrm{Sym}^{\infty}\mathrm{Sing}(X) \right| \to \mathrm{Sym}^{\infty}X$.

 

Chứng minh. Theo định lý 32 thì $j: \left|\mathrm{Sing}(X) \right| \to X$ là một đồng luân yếu nên theo định lý Whitehead cũng là một tương đương đồng luân ($\left|\mathrm{Sing}(X) \right|$ là một CW-phức). Theo bổ đề thì $\mathrm{Sym}^n j: \mathrm{Sym}^{\infty} \left| \mathrm{Sing}(X) \right| \to \mathrm{Sym}^{\infty}X$ là một tương đương đồng luân. Kết hợp với đồng luân yếu $\left| \mathrm{Sym}^{\infty} \mathrm{Sing}(X) \right| \to \mathrm{Sym}^{\infty} \left| \mathrm{Sing}(X) \right| $ ta có điều phải chứng minh.

 

Định lý 43. (Dold-Thom) Cho $K$ là một tập đơn hình liên thông khi đó $\mathrm{Sym}^n K$ cũng liên thông với $n= 0,1,...,\infty$. Hơn nữa, tồn tại một đẳng cấu tự nhiên $H_q(\mathbb{Z}K) \cong \pi_q(\mathrm{Sym}^{\infty}K)$ với mọi $q \geq 1$.

 

Bình luận. Chúng ta sẽ bình luận một chút về định lý Dold-Thom, nếu $K$ là một tập đơn hình, ta thấy rằng $\mathbb{Z}K$ sẽ là một vật đơn hình tự do trong phạm trù các nhóm abel, trong đó $(\mathbb{Z}K)_n = \mathbb{Z}K_n$. Nhưng ngoài ra $\mathrm{Sym}^{\infty}K$ cũng đóng một vai trò tương tự, nó là một vật đơn hình tự do trong phạm trù các monoid giao hoán. Như vậy theo tính phổ dụng của một vật tự do, ta sẽ có một cấu xạ tự nhiên $\mathrm{Sym}^{\infty}K \to \mathbb{Z}K$, định lý Dold-Thom nói rằng cấu xạ này cảm sinh đẳng cấu $\pi_{\bullet}(\mathrm{Sym}^{\infty}K) \overset{\cong}{\rightarrow} \pi_{\bullet}(\mathbb{Z}K) = H_{\bullet}(\mathbb{Z}K)$.

 

Hệ quả 44. Cho $X$ là một CW-phức liên thông, khi đó tồn tại một đẳng cấu tự nhiên $H_q(X) \cong \pi_q(\mathrm{Sym}^{\infty}X)$ với mọi $q \geq 1$. Nói riêng, $\mathrm{Sym}^{\infty}M(G,n) = K(G,n)$ với mọi nhóm abel $G$ và $n \geq 1$.

 

Chứng minh. Nếu $X$ liên thông thì $\mathrm{Sing}(X)$ cũng liên thông nên theo định lý 43
$$H_q(X) = H_q(\mathbb{Z}\mathrm{Sing}(X)) \cong \pi_q(\mathrm{Sym}^{\infty}\mathrm{Sing}(X)).$$ Dễ thấy $\mathrm{Sym}^{\infty}\mathrm{Sing}(X)$ là một vật đơn hình trong phạm trù các monoid abel. Theo định lý 31 ta có một đẳng cấu $\pi_q(\mathrm{Sym}^{\infty}\mathrm{Sing}(X)) \cong \pi_q(\left|\mathrm{Sym}^{\infty}\mathrm{Sing}(X) \right|)$ và lại theo hệ quả 42 thì $\pi_q(\left|\mathrm{Sym}^{\infty}\mathrm{Sing}(X) \right|) \cong \pi_q(\mathrm{Sym}^{\infty}X)$. Khẳng định thứ hai là hệ quả hiển nhiên của khẳng định thứ nhất.

 

Hệ quả 45 Cho $K$ là một tập đơn hình, khi đó tồn tại một đẳng cấu tự nhiên $H_q(\mathbb{Z}K) \cong H_q(\left|K\right|;\mathbb{Z})$ với mọi $q \geq 1$. Kết quả tương tự cũng đúng với đồng điều hệ số bất kỳ.

 

Định lý 46. Một $H$-không gian liên thông đường, giao hoán, kết hợp với một phần tử đơn vị chặt (strict) có kiểu đồng luân yếu của tích các không gian Eilenberg-MacLane.

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 17-10-2021 - 18:30

[bangbang1412]

Đối đồng điều của không gian Eilenberg-MacLane

 

Bài viết này bàn tới việc, tại sao (đối) đồng điều của không gian Eilenberg-MacLane lại khó tính? Ở đây ta sẽ bàn tới mô hình đơn hình (simplicial set) của không gian $K(G,n)$ - $G$ là một nhóm abel, $n \geq 0$. Nhắc lại không gian $K(G,n)$ được định nghĩa bởi

$$\pi_i(K(G,n)) = \begin{cases} G, & \ i = n \\ 0, & i \neq 0. \end{cases}$$

Trong đó $K(G,n)$ được xác định chính xác tới một đồng luân yếu và thậm chí tới một đồng luân nếu ta làm trong phạm trù các CW-phức. Câu hỏi là, tuy nhóm đồng luân của $K(G,n)$ đơn giản như vậy nhưng điều gì làm (đối) đồng điều của nó phức tạp? Trước tiên, ta quay về với mô hình "tổ hợp" của $K(G,n)$ và do đó phải nhắc tới định lý tương ứng Dold-Kan.

 

Định lý (tương ứng Dold-Kan). Cho $\mathscr{A}$ là một phạm trù abel, khi đó hàm tử phức chuẩn hóa $N$ là một tương đương phạm trù giữa $\mathbf{Ch}_{\geq 0}(\mathscr{A})$ và $s\mathscr{A}$. Trong đó $\mathbf{Ch}_{\geq 0}(\mathscr{A})$ là phạm trù các phức mà các vị trí $<0$ là tầm thường và $s\mathscr{A}$ là phạm trù các vật đơn hình trên $\mathscr{A}$; nói cách khác, phạm trù $\mathscr{A}^{\Delta^{op}}$.

 

(Phạm trù $\Delta$ đơn giản có các vật là $[n] = (0 < 1 <...<n)$ và cấu xạ là các ánh xạ bảo toàn thứ tự) Như vậy tồn tại một hàm tử nghịch đảo $K$ (biến một phức thành một vật đơn hình) của $N$, vấn đề đã trở nên đơn giản hơn, nhóm $G$ sẽ được đồng nhất với phức

$$...0 \to 0 \to ... \to 0 \to G (\text{vị trí 0}) \to 0.$$

Phức $KG[-n]$ do đó sẽ là một vật đơn hình Eilenberg-MacLane, lấy hình học hóa $|KG[-n]|$ cho ta một mô hình cụ thể của không gian Eilenberg-MacLane. Trước khi đi xa hơn, ta quay về một vấn đề đơn giản của hàm tử dẫn xuất: gọi $A$ là một vật trong phạm trù abel $\mathscr{A}$ và $T: \mathscr{A} \to \mathscr{A'}$ là một hàm tử cộng tính. Quy trình quen thuộc là lấy một giải thức xạ ảnh

$$P_{\bullet}: ... \to P_n \to ... \to P_1 \to P_0 \to A \to 0.$$

Sau đó xóa $A$ và lấy đồng điều của phức

$$TP^{del}_{\bullet}: ... \to TP_n \to ... TP_1 \to TP_0 \to 0, \ \ L_qT(A) = H_q(TP^{del}_{\bullet}).$$ Trước tiên có hai vấn đề cần lưu ý:

• Tại sao ta cần giả thiết $T0 = 0$? Đơn giản là để $TP_{\bullet}$ vẫn là một phức ($T(\text{vi phân}^2) = T0 = 0$) và do đó lấy được đồng điều; tại bước này ta không cần giả thiết cộng tính.
• Tại sao ta cần giả thiết cộng tính? Trả lời: là để hàm tử dẫn xuất định nghĩa một cách duy nhất từ bổ đề so sánh đồng luân của phức xây chuyền xạ ảnh. Một đồng luân $f-g=ds + sd$ chỉ giữa nguyên dạng khi hàm tử $T$ cộng tính.

Bây giờ câu hỏi là làm sao ta định nghĩa dẫn xuất của $T$ khi bỏ đi giả thiết cộng tính (vẫn cần $T0=0$)? Dold & Puppe trong một bài báo của họ đã định nghĩa khái niệm giải thức đơn hình xạ ảnh kiểu $(A,n)$, nó chỉ đơn giản là một vật đơn hình $X$ (trên $\mathscr{A}$) mà

$$H_n(X) \cong A, H_i(X) = 0 \ \forall \ i >n, X_i = 0 \ \forall i < n,$$

và định nghĩa dẫn xuất hai chỉ số của $T$ bởi

$$L_qT(A,n) = H_q(TX).$$

Ví dụ khi $\mathscr{A} = \mathscr{A'} = \mathbf{Ab}$ là phạm trù các nhóm abel thì ta có hai hàm tử không cộng tính

$$TA = \mathbb{Z}A \otimes G, \ \ T'A = \mathrm{Sym}(A) \otimes G,$$

trong đó $\mathbb{Z}, \mathrm{Sym}$ là hàm tử đại số nhóm và hàm tử đại số đối xứng. Khi $T$ là cộng tính thì $L_qT(A,n) \cong L_{q-n}TA$. Ký hiệu đồng điều hoặc đối đồng điều của $K(A,n)$ trong một vành giao hoán có đơn vị $R$ lần lượt bởi

$$H^*(K(A,n),R) = H^*(A,n;R), \ \ H_*(K(A,n),R) = H_*(A,n;R).$$

Định lý sau trả lời câu hỏi ban đầu của ta.

 

Định lý. (Dold&Puppe) Cả hai dẫn xuất $L_qT(A,n), L_qT'(A,n)$ đều đẳng cấu với $H_q(A,n;G)$.

 

Ý tưởng chứng minh. Hàm tử $T'$ phức tạp hơn - dựa vào công trình của Dold&Thom và Spanier về tích đối xứng vô hạn $SP^{\infty}$; trong khi hàm tử $T$ hầu như theo định nghĩa. Thật vậy

$$L_qT(A,n) = H_q(\mathbb{Z}[KG[-n]] \otimes G) = H_q(A,n; G),$$

trong đó ta đã dùng sự kiện đồng điều một vật đơn hình (ở đây là $KG[-n]$) là đồng điều của phức $\mathbb{Z}[X_{\bullet}]$ (ví dụ, đồng điều kỳ dị của không gian tô-pô $X$ là đồng điều của vật đơn hình $\mathrm{Sing}(X)$) và sự kiện đồng điều của vật đơn hình đẳng cấu với đồng điều của hình học hóa của nó.

 

Định lý của Dold&Puppe cho ta một câu trả lời: sự khó khăn trong tính toán (đối) đồng điều của không gian Eilenberg-MacLane xuất phát từ việc chúng là dẫn xuất của các hàm tử không cộng tính. Trong bài báo On the group $H(\Pi,n)$, II của MacLane, ông đã định nghĩa giải thức bar, một phức hoàn toàn đại số để tính $H_{\bullet}(A,n;G)$. Điều này là tự nhiên do ta định nghĩa $K(A,n)$ từ đối tượng đại số và đi tính một bất biến đại số của một không gian tô-pô thì tại sao không làm việc thuần túy đại số từ đầu? Giải thức bar có liên hệ chặt chẽ với dẫn xuất của $\mathrm{Sym}$, là cơ sở để MacLane định nghĩa cách đo độ cộng tính của một hàm tử + hàm tử đa thức và làm động lực cho Cartan, trong semináire Henri Cartan (1954-1955) tính toàn thành công $H_{\bullet}(A,n;G)$ với $G = \mathbb{Z}_p,\mathbb{Z}$ ($p$ là số nguyên tố) và $A$ là nhóm abel hữu hạn sinh.

 

Tuy nhiên, chứng minh của Cartan cực kỳ phức tạp; khi thành công với bài báo này người ta tin rằng tô-pô đại số có lẽ sắp kết thúc tuy nhiên sau đó họ nhận ra là cỗ máy tính này dù chỉ thay một chỉ tiết nhỏ cũng không thể tính toán được tiếp được. Duy chỉ phát biểu kết quả $H_{\bullet}(A,n,\mathbb{Z}_p)$ ($p$ nguyên tố lẻ) có lẽ cũng đã mất $2$ trang latex.

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 17-10-2021 - 18:24