Chào các bạn! Hôm nay mình sẽ lập ra một topic hình học, cũng không hẳn là topic, đây đơn giản chỉ là những bài hình mình đã làm và cảm thấy hay nên đăng lên cho các bạn thảo luận. Nếu bạn nào thấy hay và thú vị thì gửi lời giải lên để các bạn cùng tham khảo nhé, còn nếu dễ quá thì các bạn nói hướng cũng được để topic được sôi nổi nhé. Nếu không ai trả lời thì mình sẽ đăng giải. Coi như đây là một trang tổng hợp các bài hình. Tất nhiên trong đây vẫn có một số bài mình đã không có lời giải từ lâu đăng lên cho các bạn suy nghĩ! ![]() Mình thì không giỏi hình lắm nên có gì các bạn góp ý nhé!
Mình thì không giỏi hình lắm nên có gì các bạn góp ý nhé!
Mở hàng nha ![]()
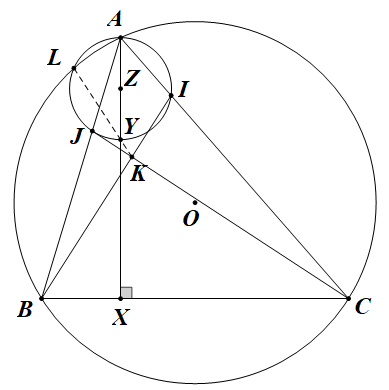
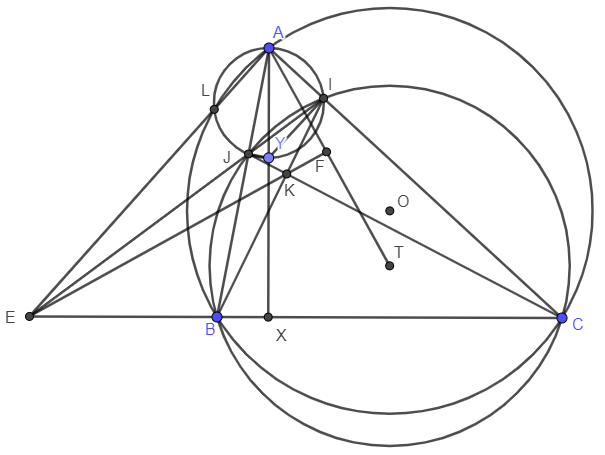
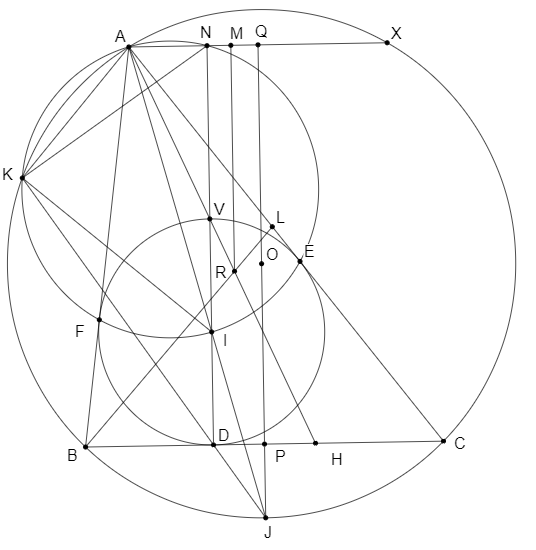
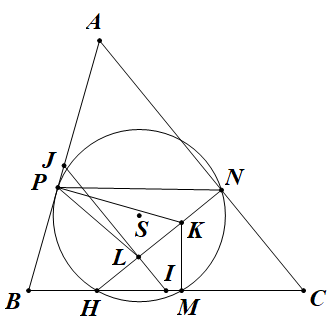
Bài 1: Cho $\Delta ABC$ nhọn ($AB<AC$) nội tiếp đường tròn $(O)$. $X$ là chân đường cao hạ từ $A$ xuống $BC$, $Y$ là một điểm di động trên $AX$. Đường tròn tâm $Z$ đường kính $AY$ cắt $AC,AB$ tại $I,J$. Đường tròn $(AIJ)$ cắt $(O)$ tại $L$. $K$ là giao điểm của $BI$ và $CJ$. Chứng minh $L,Y,K$ thẳng hàng