Chủ đề này có 4 trả lời

[bangbang1412]

In this topic, I introduce the notion of the so-called motivic integration, which is an upgrade version of the old version, namely, the p-adic integration. The word motivic literally means the values of this integration is essentially geometric. It was introduced by M. Kontsevich in his lecture in Orsay in 1995 to solve a theorem of Bartyrev stating that two birational Calabi-Yau varieties have the same Betti numbers.

 

Let $S$ be a scheme. By a $S$-algebraic variety, we mean a $S$-scheme of finite presentation. We denote by $\mathrm{Var}_S$ the isomorphism classes of finite presentation $S$-schemes. When $S = \mathrm{Spec}(k)$ with $k$ a field, we simply write $\mathrm{Var}_k$ instead of $\mathrm{Var}_{\mathrm{Spec}(k)}$.

 

Jet scheme and arc space

 

Let $X$ be a $k$-variety.

 

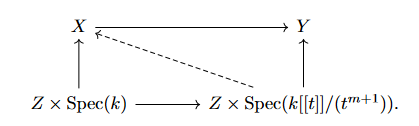
Proposition 1. For $m \in \mathbb{N}$, there exists an algebraic $k$-variety $J_m(X)$ such that:
\begin{equation*}
    \mathrm{Hom}_k(Z \times \mathrm{Spec}(k[t]/(t^{m+1})), X) \simeq \mathrm{Hom}_k(Z,J_m(X))
\end{equation*} for any $k$-scheme $Z$.

 

Proof. It is sufficient to deal with the case $X, Z$ are affine, i.e., $X = \mathrm{Spec}(R)$ and $Z = \mathrm{Spec}(A)$ for some $k$-algebra $R$ and some finitely generated $k$-algebra $R = k[x_1,...,x_n]/(f_1,...,f_r)$.
\begin{equation*}
    \mathrm{Hom}_k(\mathrm{Spec}(A) \times_k \mathrm{Spec}(k[t]/(t^{m+1})), \mathrm{Spec}(R))  \simeq \mathrm{Hom}_k(\mathrm{Spec}(A \otimes k[t]/(t^{m+1})), \mathrm{Spec}(R))
\end{equation*} which is nothing but $\left \{\varphi: k[x_1,...,x_n] \longrightarrow A[t]/(t^{m+1}) \mid \varphi(f_i) = 0 \ \forall \ i = \overline{1,r} \right \}$. For such a $\varphi$, set:
\begin{equation*}
    \varphi(x_i) = a_i^0 + a_i^1 t + \cdots + a_i^m t^m \ \forall \ i =\overline{1,n}
\end{equation*} and,
\begin{equation*}
    \varphi(f_i) = F^0_i(a^u_v) + F^1_i(a^u_v)t + \cdots + F^m_i(a^u_v) t^m
\end{equation*} where $u = \overline{0,m}, v = \overline{1,n}$ and $F^t_i$'s are polynomials in $a^{u}_v$. Consequently, we see that $\varphi(f_i)=0$ if and only if all $F^t_i(a^u_v) = 0$; and hence
\begin{align*}
    \left \{\varphi: k[x_1,...,x_n] \longrightarrow A[t]/(t^{m+1}) \mid \varphi(f_i) = 0 \ \forall \ i = \overline{1,r} \right \} &  = \mathrm{Hom}(k[x_j,x^0_j,...,x^m_j]_{j=\overline{1,n}}/(F_i^l(x^u_j)), A) \\
    & = \mathrm{Hom}(\mathrm{Spec}(A),\mathrm{Spec}(R_m))
\end{align*}
where $R_m = k[x_j,x^0_j,...,x^m_j]_{j=\overline{1,n}}/(F_i^l(x^u_j))$; and finally we can define $J_m(X) = \mathrm{Spec}(R_m)$.

 

Definition 2. For $m \geq n$, the natural surjections:
\begin{equation*}
       k[t]/(t^{m+1}) \twoheadrightarrow k[t]/(t^{n+1}) \twoheadrightarrow  k
\end{equation*} induced transition morphisms $\pi_{m,n}: J_m(X) \longrightarrow J_n(X)$, make $(J_m(X), \pi_{m,n})$ a projective system. Define $J_{\infty}(X) = \underset{m \longrightarrow \infty}{\lim} J_m(X)$ and denote by $\pi_m$ the $m^{th}$-canonical projection $\pi_m:J_m(X) \longrightarrow J(X)$.

 

Remark. It is not trivial that the limit $\underset{m \longrightarrow \infty}{\lim} J_m(X)$ exists in the category of schemes. We must prove that the transition morphisms $\pi_{m,n}$'s are affine.

 

Proposition 3. For any $k$-scheme $Z$, we have:
\begin{equation*}
    \mathrm{Hom}_k(Z \hat{\times_k}  \mathrm{Spec}(k[[t]]), X) \simeq \mathrm{Hom}_k(Z,J_{\infty}(X))
\end{equation*} where $Z \hat{\times} \mathrm{Spec}(k[[t]])$ means the formal completion of $Z \hat{\times}  \mathrm{Spec}(k[[t]])$ along the subscheme $Z \times_k \left \{0 \right \}$.

 

Definition 4. For $m \in \mathbb{N}$, the scheme $J_m(X)$ is called the $m^th$ jet scheme of $X$ and $J_{\infty}(X)$ is called the arc space of $X$. For any $k$-scheme $Z$, elements in $\mathrm{Hom}_k(Z,J_m(X))$ are called $Z$-valued $m$-jets of $X$ and elements in $\mathrm{Hom}_k(Z,J_{\infty}(X))$ are called $Z$-valued arcs of $X$. If $Z = \mathrm{Spec}(k)$, we just say $m$-jets or arcs.

 

Example 5. Let $X = V(x^3 + y^2) \subset \mathbb{A}^2_k$. View $x,y$ as formal power series in $t$ and consider the equation:
    \begin{equation*}
        (a_0+a_1t+\cdots)^3 + (b_0+b_1t+\cdots)^2 = 0.
    \end{equation*} By truncating the above equation at degree $m+1$, it gives us the defining equations of $J_m(X)$. For instance, $J_0(X)$ is given by $a_0^3+b_0^2=0$; $J_1(X)$ is given by $a_0^3+b_0^2=0$ and $3a_0^2 a_1 + 2b_0 b_1=0$.

 

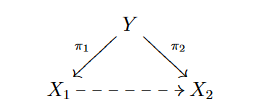
Proposition 6. Let $X \longrightarrow Y$ be an étale morphism of $k$-varieties, then $J_m(X) \cong J_m(Y) \times_Y X$ for any $m \in \mathbb{N} \cup \left \{\infty \right \}$.

 

Proof. We prove that equality on the level of functors of points. We have:
\begin{equation*}
   \mathrm{Hom}(-.J_m(X)) \simeq \mathrm{Hom}(- \times_k \mathrm{Spec}(k[[t]]/(t^{m+1})), X)
\end{equation*} and
\begin{equation*}
    \mathrm{Hom}(-,J_m(Y) \times_Y X) \simeq\mathrm{Hom}(-,J_m(Y)) \times\mathrm{Hom}(-,X) \simeq \mathrm{Hom}(- \times_k \mathrm{Spec}(k[[t]]/(t^{m+1})), Y) \times \mathrm{Hom}(-,X)
\end{equation*} For a $k$-scheme $Z$ we consider the diagram:

We have to show that  for a $Z$-valued $m$-jet of $Y$ and $Z$-valued $0$-jet of $X$ induce a $Z$-valued $m$-jet of $X$ (the other direction is obvious). Since $X \longrightarrow Y$ is étale, it is formally étale so such a dashed arrow exists.

 

Corollary 7. Let $U \hookrightarrow X$ be an open immersion, then $J_m(U) \hookrightarrow J_m(X)$ is also an open immersion for any $m \in \mathbb{N} \cup \left \{\infty \right \}$.

 

By an analogous method, we deduce the following important result:

 

Proposition 8. Let $X$ be a smooth $k$-scheme of dimension $d$. Then $J_m(X)$ is locally a $\mathbb{A}^{md}$-bundle over $X$. In particular, $J_m(X)$ is smooth of dimension $(m+1)d$. In the same way, $J_{m+1}(X)$ is locally a $\mathbb{A}^d$-bundle over $J_m(X)$.

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 13-04-2022 - 18:27

[bangbang1412]

Grothendieck ring of varieties

 

Definition 9. Let $S$ be a ring. A motivic measure $\lambda$ from the category $\mathrm{Var}_k$ with values in $S$, assigns to any $X$ in $\mathrm{Var}_k$ an element $\lambda(X)$ of $S$ such that:

• $\lambda([\mathrm{Spec}(k)]) = 1$.
• $\lambda([X]) = \lambda([Y]) + \lambda([X \setminus Y])$ for $Y$ closed in $X$.
• $\lambda([X][Y]) = \lambda([X])\lambda([Y])$ for $X, Y \in \mathrm{ob}(\mathrm{Var}_k)$.

 

Remark. Any motivic measure $\lambda$ naturally extend to take its values on constructible subsets of algebraic varieties. Indeed a constructible subset $W$ maybe written as a finite disjoint union of locally closed subvarieties $Z_i$ and hence we can define $\lambda(W)$ to be $\sum \lambda(Z_i)$. By the very axioms, this is independent of the choice of the decomposition into locally closed subvarieties.

 

Example 10. Let $k$ be a finite field and $K/k$ a finite extension, then the additive invariant $[X] \longmapsto \left | X(K) \right|$ is a motivic measure.

 

Example 11. Let $l$ be a prime number distinct from the characteristic of $k$. The assignment $$[X] \longmapsto \sum_{i=0}^{2\dim(X)}(-1)^i H_{c}^n(X,\mathbb{Q}_l)$$ where $H_c^i$ denote the $i^{th}$ $l$-adic cohomology with compact support, defines a motivic measure. This also works effectively for every other classic cohomology theories, e.g., Hodge theory, crystalline cohomology.

 

Example 12. Let us assume $k$ is a field of characterisitc zero. It follows from Deligne's mixed Hodge theory that there is a unique motivic measure $H: \mathrm{Var}_k \longrightarrow \mathbb{Z}[u,v]$, which assigns each smooth projective variety $X$ over $k$ its Hodge polynomial:
\begin{equation*}
    H(X,u,v) = \sum_{p,q}(-1)^{p+q}h^{p,q}(X)u^p v^q
\end{equation*} where $h^{p,q}(X) = \dim H^q(X,\Omega^p)$ is the $(p,q)$-Hodge number of $X$. For instance, if $k = \mathbb{C}$ then $H(\mathbb{P}^n,u,v) = \sum_{i=0}^n (uv)^i$. The uniqueness of $H$ is highly nontrivial to be proved; it is a consequence of the fact that $K_0(\mathrm{Var}_k)$ (defined below) is generated by classes of smooth proper $k$-varieties.

 

Definition 14. In the sequel, $[-]$ always denotes the isomorphism class of some object in a appropriate category. We denote by $\mathbb{Z}[\mathrm{Var}_S]$ the free abelian group on $\mathrm{Var}_S$. The Grothendieck ring over $S$ $K_0(\mathrm{Var}_S)$ is the quotient of $\mathbb{Z}[\mathrm{Var}_S]$ by its subgroup, generated by element of the form $[X] - [Z] - [X \setminus Z]$, where $X$ is a $S$-scheme of finite presentation, and $Z$ a closed subscheme of $X$. The fiber product over $S$ induces, by linearity, a ring structure on it by setting $[X] \cdot [Y] = [X \times_S Y]$. We note $\mathbf{L} = [\mathbb{A}_S^1]$ and $\mathscr{M}_S = K_0(\mathrm{Var}_S)[\mathbf{L}^{-1}]$ the localization of $K_0(\mathrm{Var}_S)$ by the element $\mathbf{L}$. When $S = \mathrm{Spec}(k)$ with $k$ a field, we simply write $\mathscr{M}_k$ instead of $\mathscr{M}_{\mathrm{Spec}(k)}$.
    
We denote by $\mathscr{M}_k[T]_{loc}$ the subring of $\mathscr{M}_k[[T]]$ generated by $\mathscr{M}_k[T]$ and the series $(1 - \mathbb{L}^a T^b)^{-1}$ with $a \in \mathbb{Z}$ and $b \in \mathbb{N} \setminus \left \{0 \right \}$.

 

Remark.

• It is evident from the very definition of $K_0(\mathrm{Var}_k)$ that it possesses a universal property: any motivic measure on $\mathrm{Var}_k$ factors through $K_0(\mathrm{Var}_k)$.
• $K_0(\mathrm{Var}_{\mathbb{C}})$ is not a domain. It was showed that there exist two abelian varieties $A, B$ such that $[A] \neq [B]$ but $A \times A \simeq B \times B$, which implies $([A] - [B])([A] + [B]) = [A]^2 - [B]^2 = 0$.
• It is proved that if $k$ has characteristic zero, then $K_0(\mathrm{Var}_k)$ can be generated by isomorphism classes of irreducible smooth projective varieties subject to the blow-up relations.

Example 15. $[\mathbb{P}_k^n] = \mathbb{L}^n + \mathbb{L}^{n-1} + \cdots + \mathbb{L} + 1$.

 

Example 16. For $k$ is algebraically closed and $X = V(x^3 - y^2)$ in $\mathbb{A}^2_k$, then $[X] = [\mathbb{A}_k^1 \setminus \left \{0\right \}] + [\left \{0 \right \}] = [\mathbb{A}^1_k] = \mathbb{L}$.

 

Example 17. For any $f: Y \longrightarrow X$ a piecewise trivial fibration with fiber $F$, i.e., $X = \coprod X_i$ locally closed and $f_{\mid f^{-1}(X_i)}: f^{-1}(X_i) \longrightarrow X_i$ is of the form (precisely, isomorphic to) $X_i \times F \longrightarrow X_i$, then:
\begin{equation*}
    [Y] = \sum [f^{-1}(X_i)] = [F] \sum [X_i] = [F][X].
\end{equation*}
For instance, for a reasonable $k$-scheme $X$, $[J_m(X)] = \mathbb{L}^{m\dim(X)}[X]$.

 

Definition 18. Let $X$ be an algebraic $k$-variety of dimension $d$ (maybe singular). A subset $C \subset J_{\infty}(X)$ is called a cylinder set if $C = \pi^{-1}_n(B_n)$ for some $n \in \mathbb{N}$ and $B_n \subset J_n(X)$ is a constructible subset, i.e., a finite disjoint union of locally closed subvarieties.

 

Remark. In a paper of Denef and Loeser, it has been proven that for any algebraic variety $X$ (not necessarily smooth), $\pi_n(J_{\infty}(X))$ is constructible for any $n \in \mathbb{N}$.

 

Definition 19. Let $X$ be a smooth $k$-variety of dimension $d$ and $C = \pi^{-1}(B_n)$ a cylinder set where $B_n \subset J_n(X)$ a constructible subset. The function:
\begin{align*}
    \widetilde{\mu}: \left \{\text{cylinder sets in} \ J_{\infty}(X) \right \} & \longrightarrow \mathscr{M}_k \\
    \pi^{-1}_n(B_n) & \longmapsto \frac{[B_n]}{\mathbb{L}^{(n+1)d}}.
\end{align*}
It is straightforward to show that $\widetilde{\mu}$ is a finitely additive measure.

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 13-04-2022 - 18:58

[bangbang1412]

Order function associated to an effective divisor

 

Let $X$ be a smooth $k$-variety of dimension $d$. Let $D$ be an effective divisor, $x$ is a point in $X$ and $g$ is a local defining equation for $D$ on a neighborhood $U$ of $x$ in $X$. For an arc $\gamma_u$ over a point $u \in U$. The intersection number $\gamma_u \cdot D$ is defined to be the order of vanishing of the formal power series $g(\gamma_u(t))=0$ at $t=0$.

 

Definition 20. Define the function $F_D$ to be:

\begin{align*}
    F_D: J_{\infty}(X) & \longrightarrow \mathbb{Z}_{\geq 0} \cup \left \{\infty \right \}\\
    \gamma_u & \longmapsto \gamma_u \cdot D.
\end{align*}

We want to integrate the function $F_D$ over $J_{\infty}(X)$ and hence we must understand the level sets $F^{-1}_D(s)$ for $s \in \mathbb{Z}_{\geq 0} \cup \left \{\infty \right \}$.

 

For an effective divisor $D = \sum_{i=1}^r a_i D_i$ ($D_i$'s are prime divisors) and $J \subset \left \{1,2,...,r \right \}$ a subset, define:
\begin{equation*}
    D_J = \begin{cases}
     \bigcap_{j \in J} D_j & \text{if} \ J \neq \varnothing, \\
     Y & \text{if} \ J = \varnothing
    \end{cases}
    \ \ \ \ \text{and} \ \ \ \
    D^{\circ}_J  = D_J \setminus \bigcup_{j \in \left \{1,2,...,r\right \}\setminus J} D_j.
\end{equation*} Recall that a divisor $D = \sum_{i=1}^r a_i D_i$ on $X$ has only simple normal crossings if at each point $x \in X$, there is a neighborhood $U$ of $x$ with coordinates $x_1,...,x_n$ for which a local defining equation for $D$ is $g = x_1^{a_{j_1}}\cdots x_{j_r}^{a_{j_x}}$ with $0 \leq j_x \leq d$.

 

Lemma 21. For $D=\sum a_i D_i$ has only simple normal crossings such that all $D_i$'s are smooth, $F^{-1}_D(s)$ is a cylinder set for $s \in \mathbb{Z}_{\geq 0}$.

 

Lemma 22. $F^{-1}_D(\infty)$ is not a cylinder set but a countable intersection of cylinder sets.

 

So far, lemma 22 tells us that $F_D$ is not $\widetilde{\mu}$-measurable ($\widetilde{\mu}$ in definition 19) because $F_D^{-1}(\infty)$ is not a cylinder set. To proceed, we have to extend $\widetilde{\mu}$ to a measure $\mu$ such that $F^{-1}_D(\infty)$ is $\mu$-measurable. We first see that $J_{\infty}(X) \setminus F_D^{-1}(\infty)$ is a countable disjoint union of cylinder sets
\begin{equation*}
    J_{\infty}(X) \setminus \pi^{-1}_0 \pi_0(F_D^{-1}(\infty)) \sqcup \bigsqcup_{n \in \mathbb{Z}_{\geq 0}} \left(\pi_n^{-1}\pi_n(F_D^{-1}(\infty)) \setminus \pi_{n+1}^{-1}\pi_{n+1}(F_D^{-1}(\infty)) \right).
\end{equation*} The above decomposition suggests us that we should extend $\widetilde{\mu}$ to a measure $\mu$ defined on the colletion of countable disjoint union of cylinder sets so that $J_{\infty}(X)\setminus F_D^{-1}(\infty)$ (and hence $F_D^{-1}(\infty)$) is $\mu$-measurable. However, countable sums are not defined in $\mathscr{M}_k = K_0(\mathrm{Var}_k)[\mathbb{L}^{-1}]$ and nothing warrants that our measure is well-defined in the sense that it is independent of the choice of the decomposition into countable disjoint union of cylinder sets. Kontsevich solved both problems at once! Follow a paper of Loeser, one should proceed by analogy with $p$-adic integration: $K_0(\mathrm{Var}_k)$ plays the role of $\mathbb{Z}$ and $K_0(\mathrm{Var}_k)[\mathbb{L}^{-1}]$ plays the role of $\mathbb{Z}[p^{-1}]$. Since in $\mathbb{R}$, $p^{-i}$ has limit $0$ as $i \longrightarrow \infty$, we should complete $K_0(\mathrm{Var}_k)[\mathbb{L}^{-1}]$ in such a way that $\mathbb{L}^{-i}$ has limit $0$ as $i \longrightarrow \infty$.

 

Definition 23. Definine $F^m$ to be the subgroup of $\mathscr{M}_k$ generated by element of the form $[S]\mathbb{L}^{-i}$ with $\dim(S)\leq i - m$. We have $F^{m+1} \subset F^m, \ \mathbb{L}^{-m} \in F^m$ and $F^m F^n \subset F^{m+n}$. We denote by $\hat{\mathscr{M}}_k$ the completion with respect to this filtration.

 

Definition 24. Let $\mathcal{C}$ denote the collection of countable disjoint unions of cylinder sets $\coprod_{i \in \mathbb{N}} C_i$ for which $\widetilde{\mu}(C_i) \longrightarrow 0$ as $i \longrightarrow \infty$, together with their complements. Extend $\widetilde{\mu}$ to a measure $\mu$ on $\mathcal{C}$ given by
\begin{equation*}
    \bigsqcup_{i \in \mathbb{N}} C_i \longmapsto \sum_{i \in \mathbb{N}}\widetilde{\mu}(C_i).
\end{equation*} It is nontrivial to show that this definition is independent of the choice of $C_i$'s.

 

Lemma 25. $\widetilde{\mu}(\pi_n^{-1}\pi_n(F_D^{-1}(\infty))) \in F^{n+1} \subset \mathscr{M}_k$.

 

Lemma 26. $F_D^{-1}(\infty)$ is $\mu$-measurable and $\mu(F_D^{-1}(\infty))= 0$.

 

Definition 27. (naive version of motivic integration). Keeping the same hypotheses on $X$ and $D$ ($D$ has only simple normal crossings), we define the motivic integral of the pair $(X,D)$ to be
\begin{equation*}
    \int_{J_{\infty}(Y)} \mathbb{L}^{-F_D}d\mu = \sum_{s \in \mathbb{Z}_{\geq 0} \cup \left \{\infty \right \} } \mu(F_D^{-1}(s))\mathbb{L}^{-s}.
\end{equation*} Since $F_D^{-1}(\infty)$ has measure zero so in fact the sum on the right is over $\mathbb{Z}_{\geq 0}$.

 

Proposition 28. With the same hypotheses as in the previous definition. Then:
\begin{equation*}
    \int_{J_{\infty}(X)} \mathbb{L}^{-F_D}d\mu = \sum_{J \subset \left \{1,2,...,r\right \}} [D^0_J]\left( \prod_{j \in J}\frac{\mathbb{L}-1}{\mathbb{L}^{a_j+1}-1} \right) \mathbb{L}^{-d}.
\end{equation*}

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 13-04-2022 - 19:56

[bangbang1412]

Motivic integration: general definition (without smoothness)

 

Let $X$ be an algebraic $k$-variety of pure dimension $d$, we want to extend our measure to a broader generality (without smoothness conditions) so that we can integrate simple functions $\alpha: J_{\infty}(X) \longrightarrow \mathbb{Z}$ whose fibers are well-understood.

 

Definition 29. Let $C$ be a constructible subset of $X$ such that $\pi_n^{-1}(B_n) = C$ for some constructible subset of $J_n(X)$. If furthermore:

• $\pi_n(C) = B_n$,
• $\pi_m(C) \subset J_{m}(X)$ is constructible for any $m \geq n$,
• The truncation morphisms $\pi_{m+1,m}: \pi_{m+1}(C) \longrightarrow \pi_m(C)$ is a piecewise trivial fibration with fiber $\mathbb{A}^d$,

then we say that $C$ is stable at level $n$. We say that $C$ is stable if it is stable at some level. When $X$ is smooth, all cylinders are stable.

 

Definition 30. Let $C$ be a stable cylinder at level $n$. We set $$\widetilde{\mu}(C) = \frac{[\pi_n(C)]}{\mathbb{L}^{(n+1)d}} \in \mathscr{M}_k$$ The stability condition ensures that this definition is independent of the choice of $n$. By proposition 8, when $X$ is smooth, all cylinder subsets are stable. In particular, $J_{\infty}(X)$ is a stable cylinder, and:
\begin{equation*}
    \widetilde{\mu}(J_{\infty}(X)) = \frac{[X]}{\mathbb{L}^{d}}.
\end{equation*} Theorem 31. There exists an algebra $\mathbf{B}_X$ . of subsets of $J_{\infty}(X)$, which contains all stable cylinders nd a unique map $\mu: \mathbf{B}_X \longrightarrow \hat{\mathscr{M}_k}$ satisfying the following conditions:

• If $C$ is a stable cylinder set, then $\mu(C) = \widetilde{\mu}(C)$.
• If $C \in \mathbf{B}_X$ is contained in $J_{\infty}(Z)$ where $Z$ is a closed subvariety of $X$ with $\dim(Z) < \dim(X)$, then $\mu(C) =0$.
• Let $(C_i)_{i \in \mathbb{N}}$ be a sequence in $\mathbf{B}_X$ such that $C_i$'s are mutually disjoint and $C = \bigsqcup C_i$ belongs to $\mathbf{B}_X$, then $\sum \mu(C_i)$ converges to $\mu(C)$ in $\hat{\mathscr{M}}_k$.
• If $C, D$ are in $\mathbf{B}_X$ with $C \subset D$, and if $\mu(D)$ belongs to the closure $\hat{F}_m$ of $F_m$ in $\hat{\mathscr{M}_k}$, then $\mu(C) \in \hat{F}_m$.

Remark. Elements in $\mathbf{B}_X$ are called semi-algebraic sets, but we do not stress to the precise definition here.

 

Definition 32. Let $C$ be in $\mathbf{B}_X$ and $\alpha: C \longrightarrow \mathbb{Z} \cup \left \{ \infty \right \}$ a function such that $\alpha^{-1}(s) \in \mathbf{B}_X$ for any $s \in \mathbb{Z} \cup \left \{ \infty \right \}$ and $\mu(\alpha^{-1}(\infty)) = 0$, we set:
\begin{equation*}
    \int_C \mathbb{L}^{-\alpha}d\mu  = \sum_{s\in \mathbb{Z}} \mu(C \cap \alpha^{-1}(s)) \mathbb{L}^{-s},
\end{equation*} in $\hat{\mathscr{M}}_k$, whenever the right hand side converges in $\hat{\mathscr{M}}_k$, in which case we say $\mathbb{L}^{-\alpha}$ is integrable on $C$.

 

Theorem 33. (Change of varibles) Let $X, Y$ be algebraic $k$-varieties of pure dimension $d$ and $h : Y \longrightarrow X$ be a proper birational morphism. Let assume $Y$ to be smooth. Let $C \in \mathbf{B}_X$ and $\alpha: J_{\infty}(X) \longrightarrow \mathbb{N}$ be a simple function. Then
\begin{equation*}
        \int_C \mathbb{L}^{-\alpha}d\mu = \int_{h^{-1}(C)} \mathbb{L}^{-\alpha \circ h - \mathrm{ord}  h^*(\Omega^d_X)} d\mu.
\end{equation*} Now we can present a rough proof of Bartyrev's theorem. The following diagram illustrates the construction of $\mathscr{M}_k$:

and it motivates the following proof.

 

Theorem 34. (Bartyrev) Let $X_1,X_2$ be two birational smooth Calabi-Yau varieties, then they have the same Hodge numbers.

 

Proof. Let $K$ denote the canonical divisor. We resolve the birational map to a Hironaka hut:

In the change of variables formula, we let $\alpha: J_{\infty}(X_1) \to \mathbb{Z} \cup \left \{ \infty \right \}$ be the zero map. Then

$$\int_{J_{\infty}(X_1)} \mathbb{L}^{-\alpha} d\mu = \mu(F^{-1}(0)) = \frac{[\pi(J_{\infty}(X_1)]}{\mathbb{L}^{(0+1)n}} = \frac{[X_1]}{\mathbb{L}^n},$$ and analogously, let $\alpha': J_{\infty}(X_2) \to \mathbb{Z} \cup \left \{ \infty \right \}.$ be the zero map, we see that $\alpha \circ (\pi_1)_{\infty} = \alpha' \circ (\pi_2)_{\infty}$, both equal the zero map. Applying the change of varibles,

$$\int_{J_{\infty}(Y)} \mathbb{L}^{-\alpha \circ (\pi_1)_{\infty} - \mathrm{ord}\pi_1^*K_{Y/X_1}}d\mu = \int_{J_{\infty}(X_2)} \mathbb{L}^{-\alpha'}d\mu = \frac{[X_2]}{\mathbb{L}^n},$$ which implies that $[X_1]=[X_2]$ in $\hat{\mathscr{M}}_{\mathbb{C}}$, we apply the Hodge polynomial to deduce the theorem.

 

Example 35. Let $D = \varnothing, X' = \mathrm{Bl}_Y(X)$ be the blow of $X$ along the smooth center $Y$ of codimension $c$ in $X$. The relative canonical divisor is $K_{X'/X}=(c-1)E$ where $E$ is the exceptional divisor of the blowup. Using the previous proposition, we have:
\begin{align*}
    \int_{J_{\infty}(X')} \mathbb{L}^{-\mathrm{ord}_{K_{X'/X}}} d\mu_{X'} & = \int_{J_{\infty}(X')} \mathbb{L}^{-\mathrm{ord}_{(c-1)E}} d\mu_{X'} \\
    & = [X' \setminus E] + \frac{[E]}{[\mathbb{P}^c]} \\
    & = [X \setminus Y ] + [Y] = [X].
\end{align*}

Thanks to the change of variables formula, we deduce the rationality of the motivic zeta function and a proof of Bartyrev's theorem.

 

Theorem 36. Let $X$ be an algebraic $k$-variety and let $A$ be a semi-algebraic subset ($\in \mathbf{B}_X$) of $J_{\infty}(X)$. The power series:
\begin{equation*}
    P_C(T) =  \sum_{n=0}^{\infty}[\pi_n(A)]T^n,
\end{equation*} considered as an element of $\mathscr{M}_k[[T]]$, is rational and belongs to $\mathscr{M}_k[T]_{loc}$.

 

Motivic zeta function and motivic nearby cycles

 

Let $k$ be a field of characteristic zero. Let us assume that $X$ is a smooth quasi-projective $k$-scheme of pure dimension $d$ and $f: X \longrightarrow \mathbb{A}_k^1$ is a flat morphism of $k$-schemes. Consider the diagram

where $i$ is the zero section of the structural morphism of the affine line and $j$ its complement. We identify $f$ with the image of $t$ under the ring morphism $k[t] \longrightarrow \Gamma(X,\mathcal{O}_X)$.

 

Definition 37. The motivic zeta function is defined as follows
\begin{equation*}
    Z_f(T) = \sum_{n \geq 1} Z^1_n T^n \in \mathscr{M}_{X_{\sigma}}[[T]],
\end{equation*} where $Z^1_n = \mathbb{L}^{-nd}[\left \{\varphi \in J_n(X) \mid f \circ \varphi = t^n + O(t^{n+1}) \right \}]  = \mathbb{L}^{-nd}[\mathscr{X}^1_n] \in \mathscr{M}_{X_{\sigma}}$.

 

Remark. The expression of $\mathscr{X}^1_n$ requires $X$ to be of pure dimension $d$. Otherwise, one has to work connected components by connected components. We also know from theorem 36 that $Z_f(T) \in \mathscr{M}_{X_{\sigma}}[T]_{loc}$.

 

Let $h: X' \longrightarrow X$ be an embedded resolution of the singularities of $(X,X_{\sigma})$. By this, we mean a proper morphism $h: Y \longrightarrow X$ with $X'$ smooth such that the restriction
\begin{equation*}
    h: X' \setminus h^{-1}(X_{\sigma}) \longrightarrow X \setminus X_{\sigma}
\end{equation*} is an isomorphism and $h^{-1}(X_{\sigma}) = \sum_{i \in I} m_i D_i$ has only simple normal crossings as a subvariety of $X'$. For $\varnothing \neq J \subset I$, we define $D_J, D_J^{\circ}$ as in the previous post. We denote by $\rho_J: \widetilde{D}^{\circ}_J \longrightarrow D_J^{\circ}$ the étale cover of $D^{\circ}_J$, locally defined as follows. For any $x \in D_J^{\circ}$, there exists an affine open neighborhood $U$ of $x$ in $X$ (for the Zariski topology), a regular sequence of elements $(t_j)_{j \in J}$ of the ring $\Gamma(U, \mathcal{O}_X)$, and a unit $u \in \Gamma(U,\mathcal{O}_X^{\times})$ such that
\begin{equation*}
    f = u \prod_{j \in J} t_j^{N_j}
\end{equation*} and such that the component $D_j \cap U$ of $D \cap U$, for any $j \in J$, can be identified with the affine closed subscheme $V(t_j)$ of $U$. The base change of $\rho_J$ along the opent immersion $U \cap D_J^{\circ} \hookrightarrow D_J^{\circ}$ is identified with the finite étale morphism of $k$-schemes
\begin{equation*}
    \mathrm{Spec}\left(\mathcal{O}_{U \cap D_J^{\circ}}[T]/(T^{N_J}- u) \right) \longrightarrow U \cap D^{\circ}_J,
\end{equation*} where the strictly positive ineger $N_J$ is the greatest common divisor of the $N_j$ for all $j \in J$.

 

Theorem 38. Let $h: X' \longrightarrow X$ be an embedded resolution of the singularities of $(X,X_{\sigma})$. Let us denote by $D = h^{-1}(X_{\sigma}) = \sum_{i\in I} m_i D_i$ the exceptional divisor of $h$, that is supposed to be a simple normal crossings divisor, with $D_i$, $i \in I$, as (reduced) irreducible components. There exist strictly positive integers $n_i$, $i \in I$, such that we have the following formulars
\begin{equation*}
    Z_f(T) = \sum_{\varnothing \neq J \subset I}(\mathbb{L}-1)^{\left|J \right|-1}[\widetilde{D}^{\circ}_J]\prod_{j \in J}\frac{1}{T^{-m_j}\mathbb{L}^{n_j}-1} \in \mathscr{M}_{X_{\sigma}}[[T]],
\end{equation*} and
\begin{equation*}
    Z_{f,x}(T)  = \sum_{\varnothing \neq J \subset I}(\mathbb{L}-1)^{\left|J \right|-1}[\widetilde{D}^{\circ}_J \cap h^{-1}(x)]\prod_{j \in J}\frac{1}{T^{-m_j}\mathbb{L}^{n_j}-1} \in \mathscr{M}_{k}[[T]],
\end{equation*} for any $x \in X_{\sigma}(k)$.

 

Definition 39. The motivic nearby cycle $\psi_f$ is defined as, thanks to the rationality of the motivic zeta function,
\begin{equation*}
    \psi_f = -\left(\underset{T \longrightarrow +\infty}{\lim} Z_f(T) \right)= \sum_{\varnothing \neq J \subset I} [\widetilde{D}^{\circ}_J](1 - \mathbb{L})^{\left|J \right|-1} \in \mathscr{M}_{X_{\sigma}}.
\end{equation*} If $x \in X_{\sigma}(k)$, we define the motivic Milnor fiber as follows.
\begin{equation*}
    \psi_{f,x} = -\left(\underset{T \longrightarrow +\infty}{\lim} Z_{f,x}(T) \right)= \sum_{\varnothing \neq J \subset I} [\widetilde{D}^{\circ}_J \cap h^{-1}(x)](1 - \mathbb{L})^{\left|J \right|-1} \in \mathscr{M}_{k}.
\end{equation*}

Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 13-04-2022 - 21:20

[Zaraki]

Hồi đầu năm cũng có học khoán về motivic integration, lúc đó có lập được một cái bảng so sánh với p-adic integration như thế này:

 

 

Link tham khảo: 

• Mihnea Popa https://people.math..../571/index.html
• Francois Loeser Arizona winter school notes
• Devlin Mallory notes Motivic integration
• Willem Veys Arc spaces, motivic integration and stringy invariants.

Trong motivic integration, Bằng có biết có công thức change of variables tổng quát cho bất kì $\alpha: C\to \mathbb{Z}\cup \{\infty\}$ thay vì chỉ $\alpha: J_{\infty}(X)\to \mathbb{N}$ không nhỉ?

Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 16-04-2022 - 07:12