Chủ đề này có 2 trả lời

[Tantran2510]

Tính $I=\int_{D}\left | 2x-x^2 - y^2\right | d(x,y)$ với D giới hạn bởi $x^2+y^2\leq 2y$

[Tantran2510]

Dùng phép đổi biến trong tọa độ cực: $\left\{\begin{matrix} x=rcos\varphi \\ y=rsin\varphi \end{matrix}\right.$ 

 

Từ $x^2+y^2 \leq 2y$ ta được $r \leq 2sin\varphi$, khi đó được miền mới: $D_{r\varphi}=\left \{ (r,\varphi)\in \mathbb{R}^2, 0\leq r \leq2sin\varphi, 0\leq \varphi \leq \pi \right \}$ 

 

TÍch phân: $I = \int _{D_{r\varphi}} r^3\left \| {2cos\varphi -r} \right \| d(r,\varphi)$

 

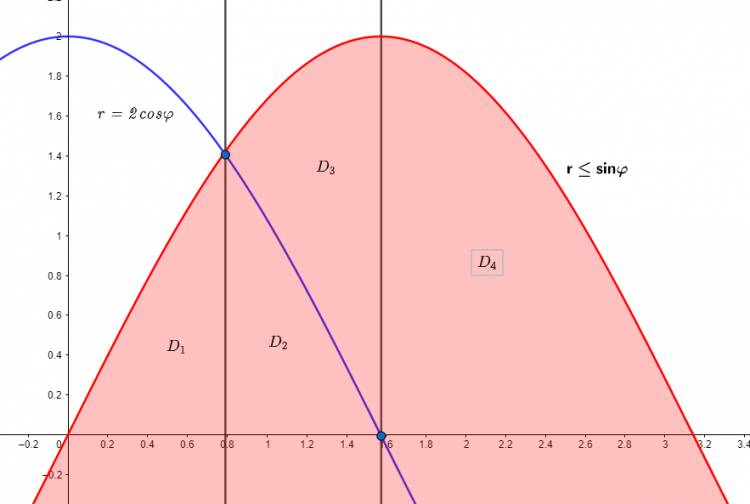
Miền $D_{r\varphi}$ là phần màu đỏ nằm trên trục Or, ta chia thành các miền $D_1, D_2, D_3, D_4$ 

 

Trong $D_1, D_2$ thì $2cos\varphi \geq r$, cụ thể là: 

$D_1=\left \{ 0\leq \varphi \leq \dfrac{\pi}{4}, 0\leq r\leq 2sin\varphi \right \}$

$D_2=\left \{ \frac{\pi}{4}\leq \varphi \leq\frac{\pi}{2}, 0\leq r\leq2cos\varphi \right \}$

 

Trong $D_3, D_4$ thì $2cos\varphi \leq r$, cụ thể là: 

$D_3=\left \{ \frac{\pi}{4}\leq \varphi \leq\frac{\pi}{2}, 2cos\varphi \leq r\leq2sin\varphi \right \}$

$D_2=\left \{ \frac{\pi}{2}\leq \varphi \leq \pi, 0\leq r\leq2sin\varphi \right \}$

 

Cuối cùng chỉ cần tính tích phân trên 4 miền đã chia

File gửi kèm

•  Untitled.png   206.38K   0 Số lần tải

[Nesbit]

Có vẻ như đổi biến $z=y-1$ thì sẽ gọn gàng hơn đấy nhỉ.