Chủ đề này có 96 trả lời

[narutosasukevjppro]

Bài 36. Cho tam giác ABC nội tiếp đường tròn (O). Gọi I, Ia lần lượt là tâm đường tròn nội tiếp, tâm đường tròn bàng tiếp góc A của tam giác ABC. Gọi AA1 là đường kính của đường tròn (O). IaA1 cắt lại đường tròn (O) tại T, AI cắt BC tại E và đường thẳng qua I vuông góc với AE cắt AC tại P. Chứng minh rằng AT, EP và BI đồng quy

Bài viết đã được chỉnh sửa nội dung bởi narutosasukevjppro: 23-08-2022 - 15:37

[DaiphongLT]

Bài 33. Cho tam giác $ABC$ nội tiếp $(O)$ và điểm $P$ bất kỳ trên $(O)$. $J,K$ là tâm đường tròn $(BOP)$ và $(COP)$. $Y,Z$ là hình chiếu của $J,K$ lên $AC,AB$. Chứng minh $YZ$ đi qua 1 điểm cố định khi $P$ di chuyển trên $(O)$

Dựng hình bình hành $OZQD$ và $DKZU$, khi đó $OKQU$ cũng là hình bình hành. Vì $KO=KD$ nên $UZ=UQ$. Gọi $(U,UV)$ cắt $AB$ tại $P$, $E$ và $F$ là hình chiếu của $D$ lên $CA$ và $AB$.
Ta có $\Delta UZQ=\Delta KOD(c-c-c)\Rightarrow \widehat{ZPQ}=\widehat{OCD}=90^{\circ}-\widehat{DAC}=\widehat{AFE}\Rightarrow PQ//EF$, mặt khác $UD//KZ$ nên $DU$ vuông $AB$ hay $D, U, F$ thẳng hàng. Do đó $Z$ và $P$ đối xứng với nhau qua $DF$. Vì vậy nếu gọi $M$ trung điểm $ZQ$ thì ta có $FM//PQ//FE$ nên $F, M, E$ thẳng hàng
Gọi $N$ trung điểm $OD$, khi đó ta có $MNOZ$ là hình bình hành, do đó nếu ta gọi $DM$ cắt $OZ$ tại $O_1$ thì ta có $ZM$ là đường trung bình của tam giác $O_1OD$. Gọi $D_1, D_2$ lần lượt là điểm đối xứng của $D$ qua $CA, AB$, vì $M$ trung điểm $OD_1$ nên $O_1$ thuộc $D_1D_2$, định nghĩa $O_2$ tương tự $O_1$, ta cũng có $O_2$ thuộc $D_1D_2$, do đó $O_1O_2$ là đường thẳng Steiner của $D$ đối với tam giác $ABC$ hay $O_1O_2$ đi qua trực tâm tam giác $ABC$. Đến đây xét phép vị tự tâm $O$, tỉ số $\frac{1}{2}$, ta được $YZ$ đi qua tâm Euler của tam giác $ABC$

[DaiphongLT]

Bài 36. Cho tam giác ABC nội tiếp đường tròn (O). Gọi I, Ia lần lượt là tâm đường tròn nội tiếp, tâm đường tròn bàng tiếp góc A của tam giác ABC. Gọi AA1 là đường kính của đường tròn (O). IaA1 cắt lại đường tròn (O) tại T, AI cắt BC tại E và đường thẳng qua I vuông góc với AE cắt AC tại P. Chứng minh rằng AT, EP và BI đồng quy

Gọi $G$ thuộc $AB$ sao cho $I_aG//IP$, ta có $\Delta AI_aG \sim \Delta AIP (g-g)$ nên $\frac{I_aG}{IP}=\frac{AI_a}{AI}=\frac{EI_a}{EI}$ hay $P, E, G$ thẳng hàng. Gọi $GI_a$ cắt $AA_1$ và $BC$ tại $J$ và $F$, $I_aA_1$ cắt $EJ$ tại $K$. Menelaus cho tam giác $JEA$ cát tuyến $A_1, K, I_a$ ta sẽ được $K$ trung điểm $EJ$. Biến đổi góc đơn giản dễ thấy $AEJF$ nội tiếp. Do đó $\widehat{EAF}=\widehat{EJI_a}=\widehat{KI_aJ}=\widehat{HA_1K}=\widehat{EIT}$ hay $A, T, F$ thẳng hàng. Để ý $(AE, II_a)=-1$ nên $BI, EP, AT$ đồng quy.

[Hoang72]

$\textbf{Bài toán 34.}$ Cho $\Delta ABC$ có $I$ là tâm đường tròn nội tiếp, $O$ là tâm đường tròn ngoại tiếp và $I_a$ là tâm đường tròn bàng tiếp đối diện đỉnh $A$. $(I)$ tiếp xúc với $BC$ tại $D$. $P$ là điểm chính giữa cung $BC$ chứa $A$ của $(O)$. $DP$ cắt $OI$ tại $L$, $PI_a$ cắt $(O)$ tại điểm thứ hai $K$. Chứng minh $A,L,K$ thẳng hàng

Từng khai thác một vài tính chất.

Gọi $Q$ là điểm chính giữa cung $BC$ không chứa $A$.

Cho $KQ$ cắt $BC$ tại $E$.

Khi đó $\overline{QK} . \overline{QE} = QB^2 = QI_a^2$

$\Rightarrow \widehat{QI_aE} = 90^\circ$.

$AI$ cắt $BC$ tại $F$, $(AI)$ cắt lại $(O)$ tại $V$.

Khi đó $V,D,Q$ thẳng hàng. 

Ta có $\frac{QI_a}{QP} = \frac{QB}{QP} = \frac{ID}{IA}$

$\Rightarrow QI_aP\sim \Delta IDA(c.g.c)$

$\Rightarrow \widehat{QPK} = \widehat{DAF}$.

Mặt khác $\overline{QD}.\overline{QV} = QB^2 = \overline{QF} . \overline{QA}$

$\Rightarrow$ Tứ giác $AVDF$ nội tiếp

$\Rightarrow \widehat{QPK} = \widehat{DVF}$

$\Rightarrow V,F,K$ thẳng hàng.

Cho $VP$ cắt $BC$ tại $X$. Ta có kết quả quen thuộc $IX\perp AD$.

$IX$ cắt lại $(BIC)$ tại $N$.

Kẻ đường kính $MK$ của $(O)$.

Dễ thấy $QI = QN$.

Ta có biến đổi góc có hướng:

$(GI,GX)\equiv (NI,NQ) \equiv (IQ,IN)\equiv (IA,IX) \equiv (IA,AD) +\frac{\pi}{2} \equiv -(PQ,PI_a)+\frac{\pi}{2} \equiv (QK,PK) + (PK,PQ) \equiv (QK,PQ) \equiv (OK,QK)\equiv (MG,GQ)\pmod \pi$.

Mà $GQ\equiv GX$, do đó $GI\equiv MG$ suy ra $G,I,M$ thẳng hàng.

Lại có dễ dàng nhận thấy $G,D,P$ thẳng hàng, do đó áp dụng định lý Pascal cho bộ $\begin{pmatrix} A & M & P \\ G & Q & K \end{pmatrix}$ ta có điều phải chứng minh.

Hình gửi kèm

• 

[DaiphongLT]

Bài 38: Cho tam giác $ABC$ $(AB<AC)$, $E$ và $F$ lần lượt nằm trên $CA, AB$ sao cho $BF=CE$, $BE$ cắt $CF$ tại $K$. $I_1, I_2$ lần lượt là tâm đường tròn nội tiếp tam giác $KBF$ và tam giác $KCE$. Phân giác trong góc $\widehat{BAC}$ cắt $I_1I_2$ tại $L$. Chứng minh $LI_1=KI_2$.

[Hoang72]

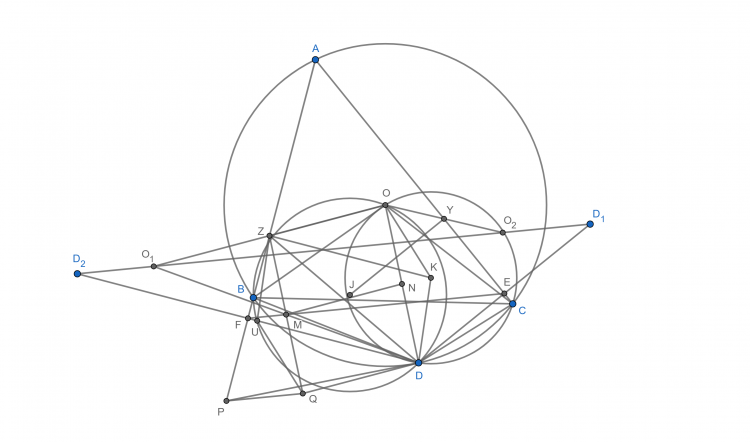
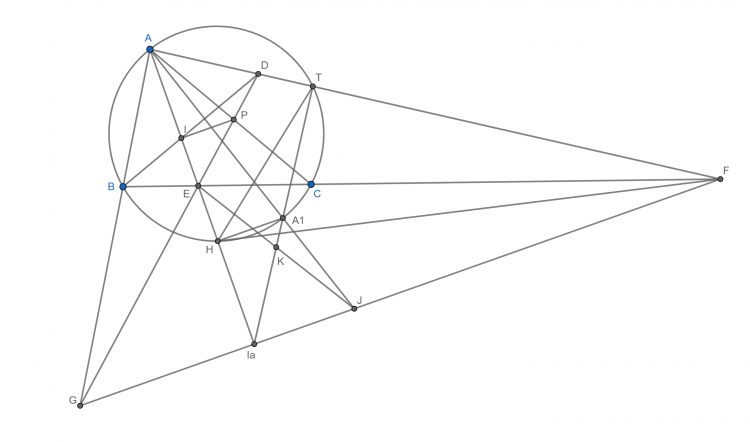
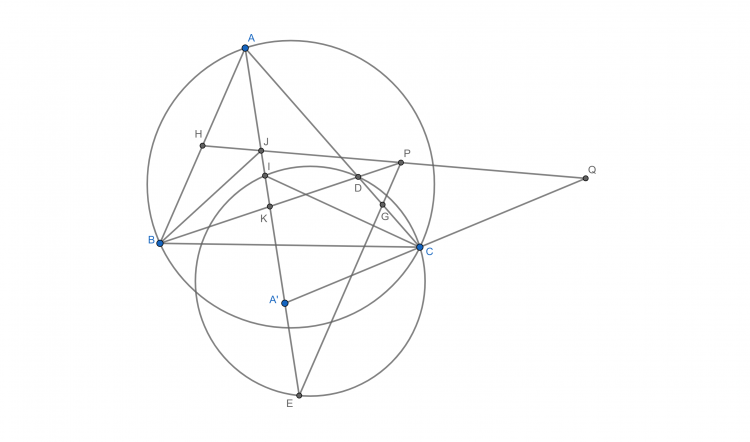
Bài 38: Cho tam giác $ABC$ $(AB<AC)$, $E$ và $F$ lần lượt nằm trên $CA, AB$ sao cho $BF=CE$, $BE$ cắt $CF$ tại $K$. $I_1, I_2$ lần lượt là tâm đường tròn nội tiếp tam giác $KBF$ và tam giác $KCE$. Phân giác trong góc $\widehat{BAC}$ cắt $I_1I_2$ tại $L$. Chứng minh $LI_1=KI_2$.

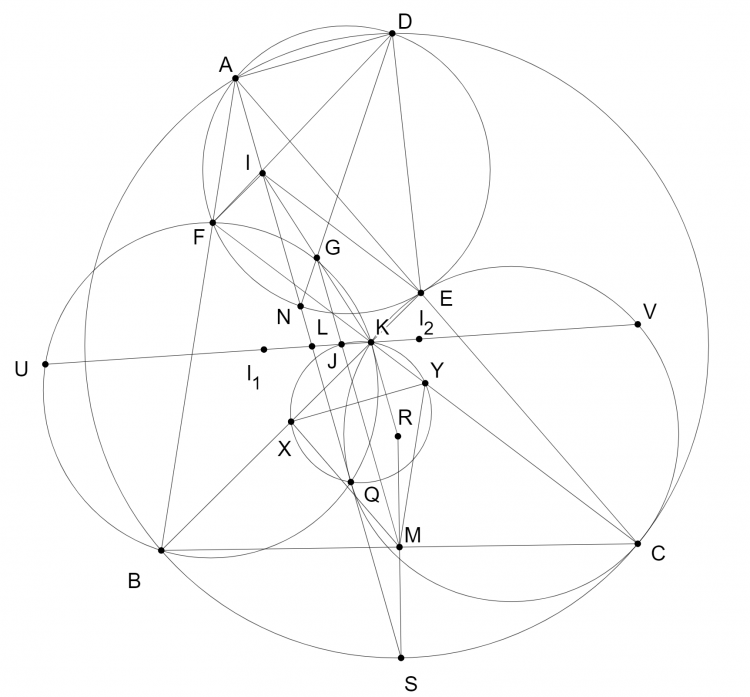
Gọi $D,S$ lần lượt là trung điểm của hai cung $BC$ chứa $A$ và không chứa $A$.

$R$ đối xứng với $S$ qua $BC$. $Q$ là điểm liên hợp đẳng giác của $R$ trong tam giác $KBC$.

Gọi $M,X,Y,G$ lần lượt là trung điểm của $BC,BE,CF,EF$.

Dễ thấy $MXGY$ là hình thoi.

$MG$ cắt $I_1I_2$ tại $J$.

Dựng hình bình hành $KEIF$.

Nhận xét 1: $JL = JK$:

Chứng minh: Ta có $\Delta DBF = \Delta DCE(c.g.c)\Rightarrow \begin{cases} D\in (AEF) \\ DE = DF\end{cases}$.

Kẻ đường kính $DN$ của $(AEF)$.

Sử dụng định nghĩa tỉ số kép dễ dàng chứng minh được $F(AE,IN) = E(AF,IN)$.

Dẫn đến $A,I,N$ thẳng hàng, hay $AI$ là phân giác $\angle BAC$.

Theo tính chất đường trung bình cho tam giác $KIL$, ta có $JK = JL$.

Nhận xét 2: $Q$ thuộc $(KBF)$ và $(KCE)$: 

Chứng minh Do $JL=JK$, theo tính chất đường trung bình hình thang ta có $KR\parallel AS$.

Ta có biến đổi góc $(QB,QK) \equiv (QB,BK) + (BK,QK) \equiv (BC,BR) + (KR,KC)\equiv (AB,AS) + (AI,KC) \equiv (AB,KC)\equiv (FB,FK)\pmod \pi$

$\Rightarrow Q\in (KBF)$, tương tự $K\in (KCE)$.

Nhận xét 3: $J,K,X,Y,Q$ đồng viên:

Chứng minh: Do $Q$ là điểm Miquel của tứ giác toàn phần $BECF.KA$ nên $Q \in (AFC)\cap (AEB)$.

Do đó xét phép vị tự quay $\mathcal{F}_{Q}$: $\begin{cases} B\mapsto F \\ E\mapsto C\end{cases}$

$\Rightarrow \mathcal{F}_{Q}(X) = Y\Rightarrow (QX,QY)\equiv (QB,QF)\equiv (KB,KF)\equiv (KX,KY)\pmod \pi$

$\Rightarrow Q\in (KXY)$.

Đồng thời do $KJ$ là phân giác ngoài của $\angle XKY$ và $JX=JY$ nên $J\in (KXY)$.

Dẫn đến $J,K,X,Y,Q$ đồng viên.

Nhận xét 4: $JI_1 = JI_2$: 

Chứng minh: Cho $I_1I_2$ cắt lại $(KBF)$ và $(KCE)$ tại $U,V$.

Dễ thấy $\Delta UBF=\Delta VCE\Rightarrow UI_1=UB=VC=VI_2$. (1)

Lại có $\frac{\wp_{X/(KBF)}}{\wp_{X/(KCE)}} = -1 = \frac{\wp_{Y/(KBF)}}{\wp_{Y/(KCE)}}$, và đường tròn $(JKXYQ)$ đồng trục với hai đường tròn này nên $\frac{\wp_{J/(KBF)}}{\wp_{J/(KCE)}} = -1$

$\Rightarrow JU = JV$. (2)

Từ (1), (2) ta có $JI_1=JI_2$.

Kết hợp với nhận xét 1 ta có điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi Hoang72: 24-08-2022 - 19:23

[nhungvienkimcuong]

Giờ nhìn hình các bạn làm khiếp thật, bỏ hình lâu quá nên giờ chẳng thể làm bài nào của các bạn cả. Mạn phép các bạn mình đăng một bài, lục lại vở cũ thấy ngày xưa mình có làm bài toán sau.

 

Bài 39: Cho tam giác $ABC$ (góc $B$ lớn hơn góc $C$) và $D$ là điểm trên $AC$ sao cho $\angle ABD =\angle C$. Đặt $I$ là tâm nội tiếp của tam giác $ABC$ và đường tròn ngoại tiếp tam giác $CDI$ cắt $AI$ ở $E$ khác $I$. Đường thẳng đi qua $E$ và song song với $AB$ cắt $BD$ ở $P$. Đặt $J$ là tâm nội tiếp tam giác $ABD$, $A’$ là điểm đối xứng với $A$ qua $I$. Goị $Q$ là giao của $JP$ và $A’C$. Chứng minh rằng $QJ=QA’$.

[DaiphongLT]

Giờ nhìn hình các bạn làm khiếp thật, bỏ hình lâu quá nên giờ chẳng thể làm bài nào của các bạn cả. Mạn phép các bạn mình đăng một bài, lục lại vở cũ thấy ngày xưa mình có làm bài toán sau.

 

Bài 39: Cho tam giác $ABC$ (góc $B$ lớn hơn góc $C$) và $D$ là điểm trên $AC$ sao cho $\angle ABD =\angle C$. Đặt $I$ là tâm nội tiếp của tam giác $ABC$ và đường tròn ngoại tiếp tam giác $CDI$ cắt $AI$ ở $E$ khác $I$. Đường thẳng đi qua $E$ và song song với $AB$ cắt $BD$ ở $P$. Đặt $J$ là tâm nội tiếp tam giác $ABD$, $A’$ là điểm đối xứng với $A$ qua $I$. Goị $Q$ là giao của $JP$ và $A’C$. Chứng minh rằng $QJ=QA’$.

Gọi $K$ là giao điểm của $AI$ và $BD$, ta có $\widehat{JED}=\widehat{ICD}=\frac{\widehat{ACB}}{2}=\frac{\widehat{ABD}}{2}=\widehat{JBD}$ hay $JBED$ nội tiếp. Do đó $E$ là tâm đường tròn bàng tiếp góc $A$ của tam giác $ABD$ hay $(AK, JE)=-1$. Mặt khác $PE//AB$ nên $PJ$ sẽ đi qua trung điểm $AB$. Gọi trung điểm $AB$ là $H$. Ta có $\Delta ABJ \sim \Delta ACI (g-g)$ nên $\Delta AHJ \sim \Delta ACA' (c-g-c)$. Vì vậy $\widehat{AJH}=\widehat{AA'C}$ hay có đpcm.

[Hoang72]

Một đẳng thức mà mình rút ra được sau khi làm một bài toán. Không biết có cách giải tự nhiên không:

Bài 40: Cho ba điểm $D,E,F$ nằm trên ba cạnh $BC,CA,AB$ của $\Delta ABC$.

Gọi $H$ là điểm Miquel ứng với ba điểm $D,E,F$ của tam giác $ABC$.

$(DEF)$ cắt $BC,CA,AB$ tại $M,N,P$. Chứng minh rằng $\frac{HE}{HF}= \frac{DE}{DF} : \frac{MN}{MP}$.

[DaiphongLT]

Bài 41: Cho tam giác $ABC$, $L$ là điểm Lemoine. $E, F$ nằm trên $CA, AB$ sao cho $LE//AB$ và $LF//AC$. Đường thẳng qua $L$ song song $EF$ cắt $CA, AB$ tại $M, N$.
$a)$ Chứng minh $MNCB$ nội tiếp đường tròn $(K)$
$b)$ Chứng minh giao điểm hai tiếp tuyến tại $M, N$ của $(K)$ nằm trên $EF$
 

[KietLW9]

$\textbf{Bài toán 42.}$ Cho $\Delta ABC$ nội tiếp $(O;R)$. Đường tròn nội tiếp $(I)$ tiếp xúc với $BC,CA,AB$ tại $A_1,B_1,C_1$. Trên tia đối của các tia $IA_1,IB_1,IC_1$ lấy các điểm $A_2,B_2,C_2$ sao cho $IA_2=IB_2=IC_2=R$. Chứng minh rằng $AA_2,BB_2,CC_2$ đồng quy tại một điểm trên $(O)$.

 

 

[KietLW9]

$\textbf{Bài toán 43.}$ Cho $\Delta ABC$ nhọn nội tiếp $(O)$. $D,E$ là hai điểm bất kì trên $AB,AC$. Đường thẳng qua $A$ vuông góc với $DE$ cắt $(ADE)$ và $(O)$ tại $P,Q$. $OP,OQ$ cắt $DE,BC$ tại $S,N$. Gọi $W$ là trực tâm $\Delta ASO$. Chứng minh rằng $S,W,O,N$ đồng viên.

[Le Tuan Canhh]

Bài toán 44.Cho tam giác ABC cân tại A và nội tiếp đường tròn (O) đường kính AK; lấy điểm I thuộc cung nhỏ AB của đường tròn (O)(I≠A,B). Gọi M là giao điểm của IK và BC, đường trung trực của đoạn thẳng IM cắt AB và AC lần lượt tại D và E. Chứng minh rằng tứ giác ADME là hình bình hành.

[MinhAnhNguyen]

Bài 30: Cho tam giác $ABC$, trực tâm $H$. $G, N_a$ là điểm Gergone, Nagel của tam giác $ABC$. $K$ là điểm liên hợp đẳng cự với $H$ trong tam giác $ABC$. Chứng minh $GN_a$ đi qua $K$

Định nghĩa $I$ là tâm nội tiếp, $I_a,I_b,I_c$ là tâm bàng tiếp

$A_1,A_2,A_3,A_4$ là hình chiếu của $A,I,I_a$ xuống $BC$, $AH'$ cắt $BC$

Cần chứng minh $A(BH',N_aG_e)=B(AH',N_aG_e)$

Đường vuông góc qua $C$ với $BC,AC$ cắt $AI_a,BI_b$ tại $D,E$

Ta có $A(BH',N_aG_e)=(BA_4,A_3A_2)=(CA_1,A_2A_3)=(DA,II_a)$

Tương tự $(B(AH',N_aG_e)=(EB,II_b)$

Tương đương với việc $AB,I_aI_b,DE$ đồng quy

Sử dụng hàng điểm điều hòa là xong

 

Bài viết đã được chỉnh sửa nội dung bởi MinhAnhNguyen: 12-09-2023 - 19:51

[Sangnguyen3]

Bài toán 45 : 
Cho $\Delta ABC$ nhọn có trực tâm $H$, đường tròn tâm $I$ qua $B,C$ và cắt $HB,HC$ lần lượt tại $E,F$. Các đường tròn $(HBF),(HCE)$ cắt nhau tại $D$ . $(J)$ là đường tròn qua $E,F$ và trung điểm $BC$ cắt $HB,HC,FB,EC$ lần lượt tại $M,N,P,Q$. Gọi $U,V$ là tâm các đường tròn $(DMP),(DNQ)$.

CMR $ID//UV$

Bài viết đã được chỉnh sửa nội dung bởi Sangnguyen3: 18-10-2023 - 10:51

[Hakubaeagle1412]

Bài toán 46 : Cho tam giác ABC nhọn (AB<AC) ; A1,B1,C1 lần lượt là chân đường phân giác hạ từ A,B,C xuống BC,CA,AB . AA1 cắt B1C1 tại A2 ; A3 đối xứng với A2 qua BC  ; B3 và C3 xác định tương tự . Chứng minh rằng : AA3,BB3,CC3 đồng quy 

[Hakubaeagle1412]

Bài toán 45 : 
Cho $\Delta ABC$ nhọn có trực tâm $H$, đường tròn tâm $I$ qua $B,C$ và cắt $HB,HC$ lần lượt tại $E,F$. Các đường tròn $(HBF),(HCE)$ cắt nhau tại $D$ . $(J)$ là đường tròn qua $E,F$ và trung điểm $BC$ cắt $HB,HC,FB,EC$ lần lượt tại $M,N,P,Q$. Gọi $U,V$ là tâm các đường tròn $(DMP),(DNQ)$.

CMR $ID//UV$

Bài này bạn có sol không cho mình xin với