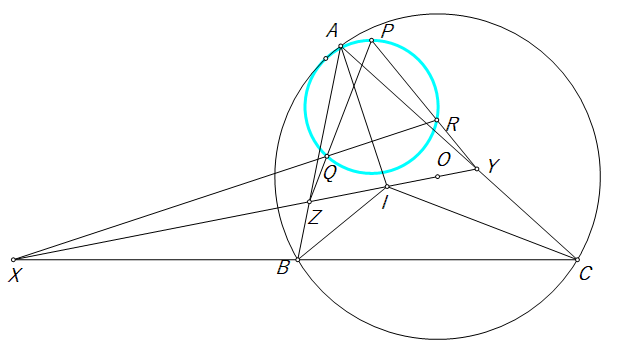
$\textbf{Bài toán}$ Cho $\Delta ABC$ nội tiếp đường tròn $(O)$, ngoại tiếp đường tròn $(I)$. $OI$ cắt $BC,CA,AB$ tại $X,Y,Z$. Đường thẳng qua $X,Y,Z$ vuông góc với $IA,IB,IC$ cắt nhau tạo thành tam giác $PQR$. Chứng minh rằng $(PQR)$ tiếp xúc $(O)$.

Chứng minh rằng $(PQR)$ tiếp xúc $(O)$.
#1
 Đã gửi 31-08-2022 - 15:39
Đã gửi 31-08-2022 - 15:39

- DOTOANNANG và Hoang72 thích
Trong cuộc sống không có gì là đẳng thức , tất cả đều là bất đẳng thức ![]()
![]()
$\text{LOVE}(\text{KT}) S_a (b - c)^2 + S_b (c - a)^2 + S_c (a - b)^2 \geqslant 0\forall S_a,S_b,S_c\geqslant 0$
#2
 Đã gửi 01-09-2022 - 21:21
Đã gửi 01-09-2022 - 21:21

$\textbf{Bài toán}$ Cho $\Delta ABC$ nội tiếp đường tròn $(O)$, ngoại tiếp đường tròn $(I)$. $OI$ cắt $BC,CA,AB$ tại $X,Y,Z$. Đường thẳng qua $X,Y,Z$ vuông góc với $IA,IB,IC$ cắt nhau tạo thành tam giác $PQR$. Chứng minh rằng $(PQR)$ tiếp xúc $(O)$.
Gọi $(I)$ tiếp xúc $BC, CA, AB$ tại $D, E, F$. Đầu tiên xét phép nghịch đảo cực $I$, phương tích $r^2$ (với $r$ là bán kính của đường tròn $(I)$), ta dễ chứng minh được $OI$ là đường thẳng Euler của tam giác $DEF$
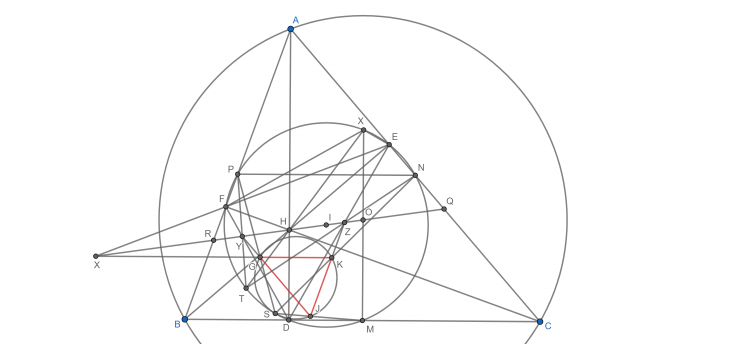
Đổi mô hình bài toán về mô hình trực tâm như sau: Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, đường cao $AD, BE, CF$ đồng quy tại trực tâm $H$. $X, Y, Z$ lần lượt là giao điểm của $OH$ với $EF, FD, DE$. Đường thẳng qua $X, Y, Z$ lần lượt vuông góc với $HD, HE, HF$ cắt nhau tạo thành tam giác $GKJ$. Chứng minh $(GKJ)$ tiếp xúc $(DEF)$.
Vai trò của tam giác $DEF$ trong bài toán này chính là tam giác $ABC$ ở bài toán gốc. Do đó $OI$ ở bài toán gốc có vai trò như $OH$ ở bài toán này.
Chứng minh: Gọi $M, N, P$ lần lượt là trung điểm $BC, CA, AB$.
Ta có $\Delta JKG \sim MNP$ (các cạnh tương ứng song song) do đó $MJ, NK, PG$ đồng quy. Gọi điểm đồng quy là $S$
Bổ đề: Gọi $OM$ cắt $(DEF)$ tại $X$. Khi đó $PY, XH, NZ$ đồng quy tại một điểm nằm trên đường tròn Euler của tam giác $ABC$. Chứng minh bổ đề này không khó, chủ yếu là liên hệ các dây cung đặc biệt và dùng định lí Pascal nhiều lần, mình xin phép không chứng minh
Quay lại bài toán, gọi $PY, XH, NZ$ đồng quy tại $T$. Ta sẽ chứng minh $\Delta PYG\sim \Delta NZK$
Thật vậy: Gọi giao điểm $OH$ với $CA, AB$ là $Q, R$, ta có $\widehat{PYG}=\widehat{PYQ}$ $+$ $\widehat{GYQ}$ $=$ $\widehat{PTN}+\widehat{NZQ}$ $+$ $\widehat{AQR}$ $=$ $\widehat{BAC}$ $+$ $\widehat{NZQ}$ $+$ $180^{\circ}$ $-$ $\widehat{BAC}$ $-$ $\widehat{ARQ}$ $=$ $\widehat{NZQ}+\widehat{KZQ}=\widehat{NZK}$ $(1)$
Tiếp theo ta sẽ chứng minh $\frac{PY}{NZ}=\frac{YG}{ZK}$ $(2)$
Ta có $\frac{YG}{ZK}=\frac{sin\widehat{YXG}.XY}{sin\widehat{YGX}}.\frac{sin\widehat{ZKX}}{XZ.sin\widehat{ZXK}}=\frac{XY}{XZ}.\frac{sin\widehat{ABC}}{sin\widehat{ACB}}=\frac{XY}{XZ}.\frac{AC}{AB}=\frac{YF}{FD}.\frac{DE}{EZ}.\frac{AC}{AB}$
Do đó ta cần chứng minh $\frac{PY}{NZ}=\frac{YF}{FD}.\frac{DE}{EZ}.\frac{AC}{AB}$ hay $\frac{PY}{YF}.\frac{EZ}{NZ}=\frac{DE}{DF}.\frac{AC}{AB}$
Ta có $\frac{PY}{YF}.\frac{EZ}{NZ}=\frac{sin\widehat{ARQ}.RY}{sin\widehat{FPY}}.\frac{sin\widehat{BFD}}{sin\widehat{ARQ}.RY}.\frac{sin\widehat{AQR}.ZQ}{sin\widehat{DEC}}.\frac{sin\widehat{ZNQ}}{sin\widehat{AQR}.ZQ}=\frac{sin\widehat{ACB}}{sin\widehat{ABC}}.\frac{sin\widehat{EXH}}{sin\widehat{FXH}}=\frac{AB}{AC}.\frac{HE.sin\widehat{XEH}}{XH}.\frac{XH}{HF.sin\widehat{XFH}}=\frac{AB}{AC}.\frac{HE}{HF}.\frac{sin\widehat{ABC}}{sin\widehat{ACB}}=\frac{AB}{AC}.\frac{HE}{HF}.\frac{AC}{AB} = \frac{HE}{HF}$
Do đó ta cần chứng minh $\frac{HE}{HF}=\frac{DE}{DF}.\frac{AC}{AB}\Leftrightarrow \frac{HE}{DE}.\frac{DF}{HF}=\frac{AC}{AB}$ (hiển nhiên đúng). Vì vậy ta có $(2)$
Từ $(1)$ và $(2)$ ta có được $\Delta PYG\sim \Delta NZK$ $(g-g)$ $\Rightarrow \widehat{PGY}=\widehat{ZKN}$ hay $GKJS$ nội tiếp. Ở Mặt khác $GK//PN$ nên ta có đpcm.
$P/s:$ bài này của anh Nguyễn Duy Phước, mọi người có thể tham khảo bài toán này và trường hợp tổng quát hơn ở đây:https://artofproblem...165960p16088122
Bài viết đã được chỉnh sửa nội dung bởi DaiphongLT: 01-09-2022 - 21:24
- Hoang72 yêu thích
ズ刀Oア
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh