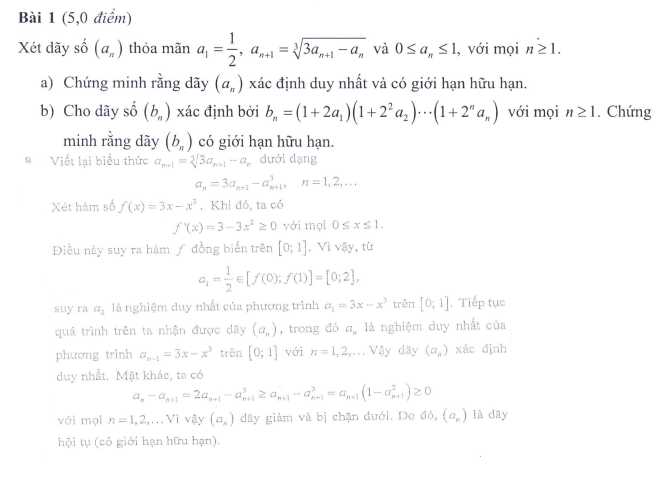Để áp dụng suy luận như trên, bạn phải tìm một khoảng ổn định của $f$, nghĩa là một khoảng/đoạn $I$ sao cho với mọi $t \in I$ thì $f(t) \in I$.
Sau đó khi bạn có $x_0 \in I$ thì bằng quy nạp sẽ có $x_n \in I$ với mọi $n$.
Tiếp theo, nếu $f$ đồng biến trên $I$ thì dãy sẽ tăng hoặc giảm, tùy theo $x_1 \ge x_0$ hay $x_1 \le x_0$.
Nếu $x_1 \ge x_0$ thì $f(x_1) \ge f(x_0)$ vì $f$ đồng biến, hay $x_2 \ge x_1$. Tiếp tục, ta có $x_3 \ge x_2$... bằng quy nạp thì $x_{n+1} \ge x_n$ với mọi $n$, hay dãy $(x_n)$ tăng.
Tương tự, nếu $x_1 \le x_0$ thì dãy $(x_n)$ giảm.
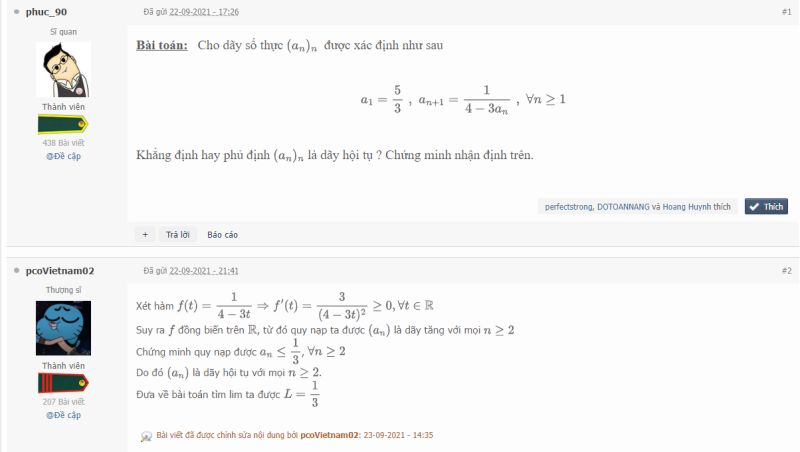
Cần nói thêm là bài làm của bạn pcoVietnam2 ở trên là chưa chặt chẽ ở đoạn này:
"$f$ đồng biến trên $\mathbb{R}$."
Kết luận này là sai, $f$ không xác định tại điểm điểm $\frac{4}{3}$. Ta chỉ có $f'(t) \ge 0$ với $t \in (-\infty, \frac{4}{3})$ và $t \in (\frac{4}{3},+\infty)$, nghĩa là $f$ chỉ đồng biến trên các khoảng $(-\infty, \frac{4}{3})$ và $(\frac{4}{3},+\infty)$ mà thôi.
$$\text{H}^r_{\text{ét}}(\mathcal{O}_K, M) \times \text{Ext}^{3-r}_{\mathcal{O}_K}(M,\mathbb{G}_m) \to \text{H}^3_{\text{ét}}(\mathcal{O}_K,\mathbb{G}_m) \cong \mathbb{Q}/\mathbb{Z}.$$
"Wir müssen wissen, wir werden wissen." - David Hilbert
![]()