Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 12-05-2023 - 21:53
Tiêu đề

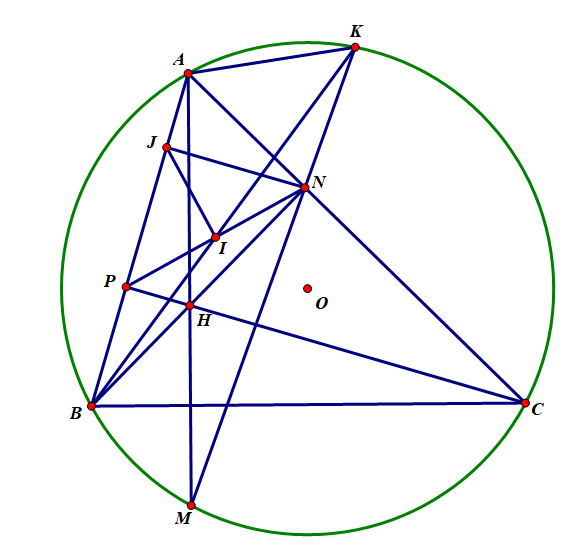
I là trung điểm của PN
#1
 Đã gửi 12-05-2023 - 21:51
Đã gửi 12-05-2023 - 21:51

- truongphat266 yêu thích
N.K.S - Learning from learners!
#2
 Đã gửi 23-05-2023 - 20:34
Đã gửi 23-05-2023 - 20:34

Trong quá trình giải bài này em tìm được 2 cách giải.Cách thứ nhất tuy dài hơn nhưng mang tính mở rộng còn cách 2 chỉ áp dụng cho bài này.Nhưng thôi,đăng cách 2 cho gọn:
Gọi $J$ là hình chiếu của $N$ lên $AB$
Ta có: $\widehat{INB}=\widehat{BAM}=\widehat{BKN}$ nên $\Delta BNI\sim \Delta BKN \Rightarrow BN^{2}=BI.BK$
Mà $BN^{2}=BJ.BA$ nên $BJ.BA=BI.BK$ suy ra $AJIK$ nội tiếp $\Rightarrow \widehat{PJI}=\widehat{AKB}=\widehat{ACB}=\widehat{APN}$
$\Rightarrow IJ=PI \Rightarrow IP=IN \Rightarrow$ $I$ là trung điểm $PN$(đpcm)
Bài viết đã được chỉnh sửa nội dung bởi huytran08: 24-05-2023 - 14:37
- perfectstrong, Le Tuan Canhh, truongphat266 và 2 người khác yêu thích
How far are you from me,Fruit?
I am hidden in your heart,Flower.
(Rabindranath Tagore)
#3
 Đã gửi 24-05-2023 - 14:24
Đã gửi 24-05-2023 - 14:24

Mà $BN^{2}=BJ.BA$ nên $BJ.BA=BI.BK$ suy ra $AJIK$ nội tiếp $\Rightarrow \textcolor{red}{\widehat{PIJ}}=\widehat{AKB}=\widehat{ACB}=\widehat{APN}$
Chỗ này là $\angle PJI$ chứ nhỉ? Nhưng nói chung kết quả vẫn đúng ![]()
Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 24-05-2023 - 14:24
- huytran08 yêu thích
$$\text{LOVE}\left( x \right)|_{x = \alpha}^\Omega = + \infty $$
I'm still there everywhere.
#4
 Đã gửi 25-05-2023 - 22:22
Đã gửi 25-05-2023 - 22:22

Trong quá trình giải bài này em tìm được 2 cách giải.Cách thứ nhất tuy dài hơn nhưng mang tính mở rộng còn cách 2 chỉ áp dụng cho bài này.Nhưng thôi,đăng cách 2 cho gọn:
Gọi $J$ là hình chiếu của $N$ lên $AB$
Ta có: $\widehat{INB}=\widehat{BAM}=\widehat{BKN}$ nên $\Delta BNI\sim \Delta BKN \Rightarrow BN^{2}=BI.BK$
Mà $BN^{2}=BJ.BA$ nên $BJ.BA=BI.BK$ suy ra $AJIK$ nội tiếp $\Rightarrow \widehat{PJI}=\widehat{AKB}=\widehat{ACB}=\widehat{APN}$
$\Rightarrow IJ=PI \Rightarrow IP=IN \Rightarrow$ $I$ là trung điểm $PN$(đpcm)
Mạo muội đoán mò, cách còn lại chắc bạn sẽ sử dụng đến một vài tính chất của trực tâm như:
(ở đây gọi E là giao điểm HM và BC)
+ E là trung điểm của HM
+ NB là phân giác của góc PNE
và 2 lần xét tam giác đồng dạng g.g rồi c.g.c ![]()
![]()
![]()
Bài viết đã được chỉnh sửa nội dung bởi thvn: 25-05-2023 - 22:28
N.K.S - Learning from learners!
#5
 Đã gửi 26-05-2023 - 07:19
Đã gửi 26-05-2023 - 07:19

Mạo muội đoán mò, cách còn lại chắc bạn sẽ sử dụng đến một vài tính chất của trực tâm như:
(ở đây gọi E là giao điểm HM và BC)
+ E là trung điểm của HM
+ NB là phân giác của góc PNE
và 2 lần xét tam giác đồng dạng g.g rồi c.g.c


thầy đoán trúng quá,cách đấy hơi dài nên em đăng cách còn lại lên
- thvn yêu thích
How far are you from me,Fruit?
I am hidden in your heart,Flower.
(Rabindranath Tagore)
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh