Cho tam giác $ABC$ có trực tâm $H$ và các cạnh $a,b,c$. Gọi $x,y,z$ lần lượt là khoảng cách từ $H$ đến các cạnh $BC,CA,AB$. Chứng minh rằng:
$4 \left(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z} \right) = \left(-\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}\right) \left( \dfrac{a}{x}-\dfrac{b}{y}+\dfrac{c}{z} \right) \left( \dfrac{a}{x}+\dfrac{b}{y}-\dfrac{c}{z} \right)$ (1)
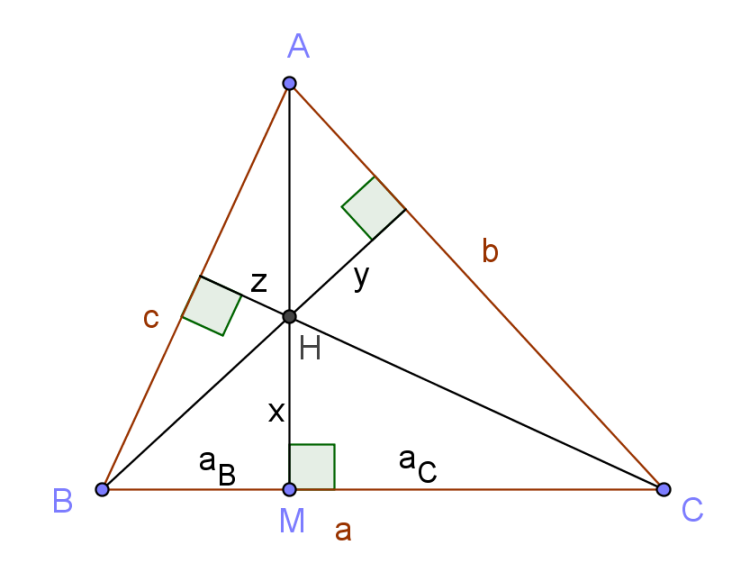
$\Delta BHM\sim\Delta ACM\Rightarrow \frac{HM}{BM}=\frac{CM}{AM}\Rightarrow MB.MC=MH.MA\Rightarrow a_B.a_C=x.h_A$
$\Rightarrow \frac{a}{x}=\frac{a.h_A}{a_B.a_C}=\frac{(a_B+a_C).h_A}{a_B.a_C}=\frac{h_A}{a_B}+\frac{h_A}{a_C}=\tan B+\tan C$
CMTT ta có : $\frac{b}{y}=\tan C+\tan A$ và $\frac{c}{z}=\tan A+\tan B$
Suy ra : VT(1)$=8.(\tan A+\tan B+\tan C)$ và VP(1)$=8.\tan A.\tan B.\tan C$
Mà $\tan A=\tan (B+C)=\frac{\tan B+\tan C}{1-\tan B.\tan C}\Rightarrow \tan A+\tan B+\tan C=\tan A.\tan B.\tan C$
Vậy VT(1) = VP(1) (đpcm) $\boxed{}$
Bài viết đã được chỉnh sửa nội dung bởi Kool LL: 02-08-2014 - 23:30







