Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 13-01-2013 - 20:40

CMR : tổng bình phương các khoảng cách từ các đỉnh của tam giác đều $ABC$ nội tiếp đường tròn $(O,R)$ đến đường thẳng $d$ bất kỳ qua $O$ không đổi
#1
 Đã gửi 02-11-2007 - 23:00
Đã gửi 02-11-2007 - 23:00

#2
 Đã gửi 14-01-2013 - 00:30
Đã gửi 14-01-2013 - 00:30

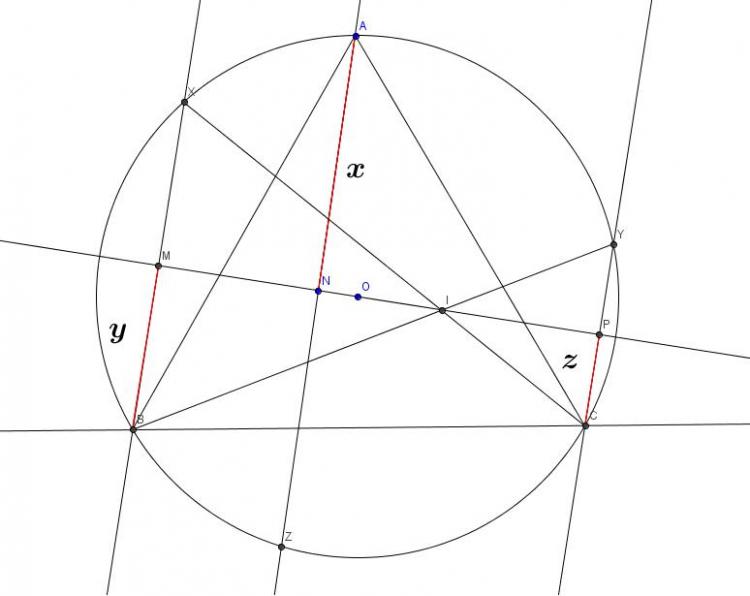
Giả sử $A$ nằm khác phía $B,C$ đối với dt $d$
Ta vẽ: $AN$ vuông góc $d$ và cắt $(O)$ ở $Z$
$BM$ vuông góc $d$ và cắt $(O)$ ở $X$
$CP$ vuông góc $d$ và cắt $(O)$ ở $Y$
đặt $BM=y=>BX=2y$
$AN=x=>AZ=2x$
$CP=z=>CY=2z$
Gọi giao điểm $CX$ và $BY$ là $I$ dễ dàng chứng minh được : $M,N,P,I$ thẳng hàng
ta có $\Delta{XBI}$ cân tại $I$ mà $BXC=60 =>\Delta{XBI}$ đều
Đặt $BX=2y=XI=IB=a_2$
CMTT $\Delta{ICY}$ đều Đặt $CY=2z=CI=YI=a_1$
** chứng minh $AZ=a_1+a_2=2x$
Ta có: $BX//AZ=> ZX=AB=AC=>...=> AX//CZ=> CX=AZ=a_1+a_2$ (dễ nhận ra)
đẳng thức cần tìm bằng $a_1^2+a_2^2+(a_1+a_2)^2= 4R^2(sin^2 \widehat{BCZ} + sin^2 \widehat{XCB} + sin^2 \widehat{ACZ})$
Đặt $\widehat{BCZ}=t$
Ta có $sin^2\widehat{BCZ}+sin^2\widehat{XCB}+sin^2\widehat{ACZ}$
$=sin^2\widehat{BCZ}+sin^2(\widehat{XCZ}-\widehat{BCZ})+sin^2(\widehat{XCZ}+\widehat{XCA})$
$=sin^2t+sin^2(60-t)+sin^2(60+t)$ (chứng minh được $\widehat{BCZ}=\widehat{XCA}$)
với biểu thức vừa biến đổi ra: Ta hoàn toàn chứng minh được đó là một hằng số bằng những phép biến đổi thông thường $sin^2t+sin^2(60-t)+sin^2(60+t)=\frac{3}{2}$
Vậy $a_1^2+a_2^2+(a_1+a_2)^2= 6R^2$
$=>x^2+y^2+z^2=\frac{3}{2}R^2$ (đpcm)
hình đây các bạn
Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 14-01-2013 - 22:27
- BlackSelena, triethuynhmath và Yii thích
#3
 Đã gửi 14-01-2013 - 00:57
Đã gửi 14-01-2013 - 00:57

Cách 3: Gọi $H, I, K$ lần lượt là chân các đường cao kẻ từ $A, B, C$ xuống đường thẳng $d$, gọi $AH,BI,CK$ lần lượt cắt $(O)$ tai điểm thứ 2$D, E, F$. Dễ thấy $DBEC$, $DBFC$ la hình thang cân =>$BE=DC, CF= DB$ => $AH^2+BI^2+CK^2= \frac{1}{4}(DA^2+BE^2+CF^2)=\frac{1}{4}(DA^2+DB^2+DC^2)=\frac{1}{4}.6R^2=\frac{3}{2}R^2$ (ko đổi)
Mở rộng: Cho hình vuông $ABCD$ có tâm $O$. CMR tổng bình phương các khoảng cách từ các đỉnh của hìng vuông đến đường thẳng $d$ bất kỳ qua $O$ không đổi
CM: Chọn hệ trục tọa độ sao cho O là gốc tọa độ, $AB$//$Oy$, $AC$//$Ox$, gọi độ dài cạnh hình vuông là 2a. Ta có $A(-a;a);B(-a;-a);C(a;-a);D(a;a)$. => $d(A/d)^2+d(B/d)^2+d(C/d)^2+d(D/d)^2=\frac{(ta+a)^2+(a-ta)^2+(ta+a)^2+(ta-a)^2}{t^2+1}=2a^2$
Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 14-01-2013 - 22:26
#4
 Đã gửi 14-01-2013 - 20:52
Đã gửi 14-01-2013 - 20:52

Anh giải thích rõ hơn được không: $d(A/d)^2+d(B/d)^2+d(C/d)^2+d(D/d)^2=\frac{(ta+a)^2+(a-ta)^2+(ta+a)^2+(ta-a)^2}{t^2+1}=2a^2$ không hiều: t là gì d(c/d)^2 để làm gì?CM: Chọn hệ trục tọa độ sao cho O là gốc tọa độ, $AB$//$Oy$, $AC$//$Ox$, gọi độ dài cạnh hình vuông là 2a. Ta có $A(-a;a);B(-a;-a);C(a;-a);D(a;a)$. => $d(A/d)^2+d(B/d)^2+d(C/d)^2+d(D/d)^2=\frac{(ta+a)^2+(a-ta)^2+(ta+a)^2+(ta-a)^2}{t^2+1}=2a^2$
Cám ơn nhiều.
Bài viết đã được chỉnh sửa nội dung bởi quagn1998: 14-01-2013 - 20:53
#5
 Đã gửi 15-01-2013 - 09:21
Đã gửi 15-01-2013 - 09:21

ÀAnh giải thích rõ hơn được không: $d(A/d)^2+d(B/d)^2+d(C/d)^2+d(D/d)^2=\frac{(ta+a)^2+(a-ta)^2+(ta+a)^2+(ta-a)^2}{t^2+1}=2a^2$ không hiều: t là gì d(c/d)^2 để làm gì?
Cám ơn nhiều.
#6
 Đã gửi 18-01-2013 - 19:08
Đã gửi 18-01-2013 - 19:08

Theo như đề bài thì mình cũng có đặt ra 1 câu hỏi: Lẽ nào với mọi đa giác đều $n$ đỉnh đều có tổng bình phương các đường cao kẻ từ các đỉnh xuống đường thẳng bất kì qua tâm đều là hẳng số ?????
Sau khi tìm hiểu thì, kết quả là:
Với $n=3$($n$ là số đỉnh) các đỉnh là $A_1,A_2,A_3$, chiếu $A_i$ xuống $d$ thành $A_i'$
Đặt $R=1$ gọi $x$ là góc tạo bởi $OA_1$ và $d$
$\sum_{i=1}^{3}A_i'O^2=cos^2x+cos^2(x+\frac{2\pi}{3})+cos^2(x+\frac{4\pi}{3})=\frac{3}{2}$
Ta có $\sum_{i=1}^{3}A_iA_i'^2=3R^2-\sum_{i=1}^{3}A_i'O^2$
=>$\sum_{i=1}^{3}A_iA_i'^2$ không đổi
Với trường hợp tổng quát:
$\sum_{i=1}^{n}A_i'O^2=\sum_{k=0}^{n-1}cos^2(x+k\frac{2\pi}{n})$ cũng 0 phụ thuộc vào $x$ (các bạn tự kiểm tra)
vậy $\sum_{i=1}^{n}A_iA_i'^2$ không đổi
Lí do: các hình chiếu của $OA_i (i=1,2,3,...,n)$ xuống d không phụ thuộc vào $d$ vào $OA_i$ bằng nhau tạo với $d$ các góc lập thành cấp số cộng công sai $\frac{2\pi}{n}$
Mở rộng 2:
Vậy trong không gian? Tứ diện đều cũng mang tính chất tương tự? Mình cũng 0 bik có đúng không các bạn nghĩ thử xem?
- triethuynhmath yêu thích
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh