cho mình hỏi về vấn đề vấn đề frobenius các kết quả đã có là thế nào

vấn đề frobenius
Bắt đầu bởi prime, 14-06-2005 - 20:36
#1
 Đã gửi 14-06-2005 - 20:36
Đã gửi 14-06-2005 - 20:36

#2
 Đã gửi 15-06-2005 - 23:46
Đã gửi 15-06-2005 - 23:46

Bạn phải nói cụ thể hơn để các bạn khác cùng biết chứ. Ai biết vấn đề Frobenius là cái gì ? Nhiều thứ liên quan có thể gọi là vấn đề Frobenius thì sao.
Thân lừa ưa cử tạ ! 
#3
 Đã gửi 16-06-2005 - 20:27
Đã gửi 16-06-2005 - 20:27

van de nay la
a1,..,ad, la cac so nguyen to cung nhau
linear diophantine problem of frobenius la tim so tu nhien n lon nhat ko bieu dien tuyen tinh qua a1,...,ad voi cac he so nguyen khong am
ban co the search theo tu khoa tren, tiec la minh chua tim duoc nhieu va no
a1,..,ad, la cac so nguyen to cung nhau
linear diophantine problem of frobenius la tim so tu nhien n lon nhat ko bieu dien tuyen tinh qua a1,...,ad voi cac he so nguyen khong am
ban co the search theo tu khoa tren, tiec la minh chua tim duoc nhieu va no
#4
 Đã gửi 17-06-2005 - 11:08
Đã gửi 17-06-2005 - 11:08

Thứ này thuộc về number theory rồi,mà mình thì không rành lắm.Cho mình hỏi cắt ngang một tí nhé prime :
Bạn nói là vấn đề là tìm số tự nhiên lớn nhất không biểu diễn tuyến tính qua các số nguyên tố cùng nhau ban đầu.
Mình muốn hỏi là
1)liệu có chứng minh được là tồn tại số tự nhiên đó hay không tức là khi n đủ lớn thì luôn biểu diễn tuyến tính được qua các số nguyên tố cùng nhau ban đầu ấy mà.
2)Chỉ số d cụ thể là rất quan trọng đúng không?Có phải là d=2,d=3,... thì cho những kết luận khác nhau không hay là lúc nào cũng có những kết luận tổng quát cho loại bài toán này?
Bạn nói là vấn đề là tìm số tự nhiên lớn nhất không biểu diễn tuyến tính qua các số nguyên tố cùng nhau ban đầu.
Mình muốn hỏi là
1)liệu có chứng minh được là tồn tại số tự nhiên đó hay không tức là khi n đủ lớn thì luôn biểu diễn tuyến tính được qua các số nguyên tố cùng nhau ban đầu ấy mà.
2)Chỉ số d cụ thể là rất quan trọng đúng không?Có phải là d=2,d=3,... thì cho những kết luận khác nhau không hay là lúc nào cũng có những kết luận tổng quát cho loại bài toán này?
Lạy chúa!
Con không hề hoài nghi tí nào về sự hiện hữu hoài nghi của người nhưng con hoài nghi rất nhiều về sự minh mẫn và công bình của người!
Con không hề hoài nghi tí nào về sự hiện hữu hoài nghi của người nhưng con hoài nghi rất nhiều về sự minh mẫn và công bình của người!
#5
 Đã gửi 17-06-2005 - 21:11
Đã gửi 17-06-2005 - 21:11

ok để mình noi qua về vấn đề này cho mọi người cùng xem:
1) do ( a_{1},..., a_{d} )=1 nên mọi số tư nhiên đều có thể biểu thị tuyến tính qua a_{1},..., a_{d} với hệ số nguyên, tức là phương trình điôphang
x.a1+y.a2+...+z.ad=n luôn có nghiêm nguyên với mọi n.
luôn có nghiêm nguyên với mọi n.
2) Vấn đề frobenius là nghiên cứu phương trình trên trong trường hợp nghiệm là nguyên không âm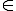 0.
0.
định lí sau là cơ sở cho các nghiên cứu:
định lí: cho a_{1},..., a_{d} là các số nguyên dương sao cho
(a1,...,ad)=1
Nếu
n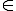
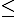
thì (* )luôn có nghiệm nguyên không âm.
chứng minh.
theo 1) luôn tôn tại z_{1},..., z_{d} để
z_{1}.a_{1}+ ..+z_{d}a_{d} .= n.
chia từng z_{i} với i=1...k-1 cho a_{d} ta có
z_{i}=a_{d}q_{i}+x_{i} và 0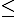 x_{i}
x_{i} 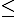 a_{d}-1
a_{d}-1
đặt
x_{d}=z_{d}+ :limits_{i=1}^{d-1} a_{i} q_{i}.
:limits_{i=1}^{d-1} a_{i} q_{i}.
thì
n= z_{1}.a_{1} +..+z_{d}a_{d}
= x_{1}.a_{1} +..+zx_{d-1}a_{d-1}+ a_{d}(z_{d}+ :limits_{i=1}^{d-1} a_{i} q_{i}.)
:limits_{i=1}^{d-1} a_{i} q_{i}.)
=x_{1}.a_{1} +..+x_{d-1}a_{d-1}+ x_{d}a_{d}
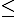 (a_{d}-1)
(a_{d}-1)  :limits_{i=1}^{d-1} a_{i}
:limits_{i=1}^{d-1} a_{i}
+ x_{d}a_{d}
ở đó x_{d} là nguyên nhưng có thể âm. tuy nhiên nếu
n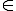 (a_{d}-1)
(a_{d}-1)  :limits_{i=1}^{d-1} a_{i} ,
:limits_{i=1}^{d-1} a_{i} ,
thì x_{d}a_{d}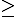 0 nên x_{d}
0 nên x_{d} 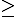 0
0
vậy dịnh lí được chứng minh
người ta kí hiệuG( a_{1},..., a_{d}) là số tư nhiên bé nhất đê mọi số tự nhiên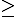 G( a_{1},..., a_{d}) đều biểi thị qua các số nguyên không âm
G( a_{1},..., a_{d}) đều biểi thị qua các số nguyên không âm
từ đinh lí trên ta có
G( a_{1},..., a_{d})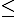 ( a_{d} -1)
( a_{d} -1)  :limits_{i=1}^{d-1} a_{i}
:limits_{i=1}^{d-1} a_{i}
Đây chính là vấn đề frobenius
lần sau mình sẽ nói thêm về d=2,3..
d=2 thì dã được giải quyết còn lại thì chưa.
1) do ( a_{1},..., a_{d} )=1 nên mọi số tư nhiên đều có thể biểu thị tuyến tính qua a_{1},..., a_{d} với hệ số nguyên, tức là phương trình điôphang
x.a1+y.a2+...+z.ad=n
2) Vấn đề frobenius là nghiên cứu phương trình trên trong trường hợp nghiệm là nguyên không âm
định lí sau là cơ sở cho các nghiên cứu:
định lí: cho a_{1},..., a_{d} là các số nguyên dương sao cho
(a1,...,ad)=1
Nếu
n
thì (* )luôn có nghiệm nguyên không âm.
chứng minh.
theo 1) luôn tôn tại z_{1},..., z_{d} để
z_{1}.a_{1}+ ..+z_{d}a_{d} .= n.
chia từng z_{i} với i=1...k-1 cho a_{d} ta có
z_{i}=a_{d}q_{i}+x_{i} và 0
đặt
x_{d}=z_{d}+
thì
n= z_{1}.a_{1} +..+z_{d}a_{d}
= x_{1}.a_{1} +..+zx_{d-1}a_{d-1}+ a_{d}(z_{d}+
=x_{1}.a_{1} +..+x_{d-1}a_{d-1}+ x_{d}a_{d}
+ x_{d}a_{d}
ở đó x_{d} là nguyên nhưng có thể âm. tuy nhiên nếu
n
thì x_{d}a_{d}
vậy dịnh lí được chứng minh
người ta kí hiệuG( a_{1},..., a_{d}) là số tư nhiên bé nhất đê mọi số tự nhiên
từ đinh lí trên ta có
G( a_{1},..., a_{d})
Đây chính là vấn đề frobenius
lần sau mình sẽ nói thêm về d=2,3..
d=2 thì dã được giải quyết còn lại thì chưa.
#6
 Đã gửi 17-06-2005 - 21:12
Đã gửi 17-06-2005 - 21:12

ok để mình noi qua về vấn đề này cho mọi người cùng xem:
1) do ( a_{1},..., a_{d} )=1 nên mọi số tư nhiên đều có thể biểu thị tuyến tính qua a_{1},..., a_{d} với hệ số nguyên, tức là phương trình điôphang
x.a1+y.a2+...+z.ad=n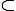 luôn có nghiêm nguyên với mọi n.
luôn có nghiêm nguyên với mọi n.
2) Vấn đề frobenius là nghiên cứu phương trình trên trong trường hợp nghiệm là nguyên không âm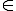 0.
0.
định lí sau là cơ sở cho các nghiên cứu:
định lí: cho a_{1},..., a_{d} là các số nguyên dương sao cho
(a1,...,ad)=1
Nếu
n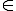 ( a_{d} -1)
( a_{d} -1) 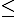 :limits_{i=1}^{d-1} a_{i}
:limits_{i=1}^{d-1} a_{i}
thì (* )luôn có nghiệm nguyên không âm.
chứng minh.
theo 1) luôn tôn tại z_{1},..., z_{d} để
z_{1}.a_{1}+ ..+z_{d}a_{d} .= n.
chia từng z_{i} với i=1...k-1 cho a_{d} ta có
z_{i}=a_{d}q_{i}+x_{i} và 0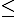 x_{i}
x_{i} 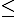 a_{d}-1
a_{d}-1
đặt
x_{d}=z_{d}+ :limits_{i=1}^{d-1} a_{i} q_{i}.
:limits_{i=1}^{d-1} a_{i} q_{i}.
thì
n= z_{1}.a_{1} +..+z_{d}a_{d}
= x_{1}.a_{1} +..+zx_{d-1}a_{d-1}+ a_{d}(z_{d}+ :limits_{i=1}^{d-1} a_{i} q_{i}.)
:limits_{i=1}^{d-1} a_{i} q_{i}.)
=x_{1}.a_{1} +..+x_{d-1}a_{d-1}+ x_{d}a_{d}
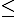 (a_{d}-1)
(a_{d}-1)  :limits_{i=1}^{d-1} a_{i}
:limits_{i=1}^{d-1} a_{i}
+ x_{d}a_{d}
ở đó x_{d} là nguyên nhưng có thể âm. tuy nhiên nếu
n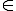 (a_{d}-1)
(a_{d}-1)  :limits_{i=1}^{d-1} a_{i} ,
:limits_{i=1}^{d-1} a_{i} ,
thì x_{d}a_{d}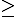 0 nên x_{d}
0 nên x_{d} 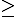 0
0
vậy dịnh lí được chứng minh
người ta kí hiệuG( a_{1},..., a_{d}) là số tư nhiên bé nhất đê mọi số tự nhiên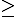 G( a_{1},..., a_{d}) đều biểi thị qua các số nguyên không âm
G( a_{1},..., a_{d}) đều biểi thị qua các số nguyên không âm
từ đinh lí trên ta có
G( a_{1},..., a_{d})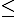 ( a_{d} -1)
( a_{d} -1)  :limits_{i=1}^{d-1} a_{i}
:limits_{i=1}^{d-1} a_{i}
Đây chính là vấn đề frobenius
lần sau mình sẽ nói thêm về d=2,3..
d=2 thì dã được giải quyết còn lại thì chưa.
1) do ( a_{1},..., a_{d} )=1 nên mọi số tư nhiên đều có thể biểu thị tuyến tính qua a_{1},..., a_{d} với hệ số nguyên, tức là phương trình điôphang
x.a1+y.a2+...+z.ad=n
2) Vấn đề frobenius là nghiên cứu phương trình trên trong trường hợp nghiệm là nguyên không âm
định lí sau là cơ sở cho các nghiên cứu:
định lí: cho a_{1},..., a_{d} là các số nguyên dương sao cho
(a1,...,ad)=1
Nếu
n
thì (* )luôn có nghiệm nguyên không âm.
chứng minh.
theo 1) luôn tôn tại z_{1},..., z_{d} để
z_{1}.a_{1}+ ..+z_{d}a_{d} .= n.
chia từng z_{i} với i=1...k-1 cho a_{d} ta có
z_{i}=a_{d}q_{i}+x_{i} và 0
đặt
x_{d}=z_{d}+
thì
n= z_{1}.a_{1} +..+z_{d}a_{d}
= x_{1}.a_{1} +..+zx_{d-1}a_{d-1}+ a_{d}(z_{d}+
=x_{1}.a_{1} +..+x_{d-1}a_{d-1}+ x_{d}a_{d}
+ x_{d}a_{d}
ở đó x_{d} là nguyên nhưng có thể âm. tuy nhiên nếu
n
thì x_{d}a_{d}
vậy dịnh lí được chứng minh
người ta kí hiệuG( a_{1},..., a_{d}) là số tư nhiên bé nhất đê mọi số tự nhiên
từ đinh lí trên ta có
G( a_{1},..., a_{d})
Đây chính là vấn đề frobenius
lần sau mình sẽ nói thêm về d=2,3..
d=2 thì dã được giải quyết còn lại thì chưa.
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh



