Thời gian làm bài: 150 phút (Không kể thời gian giao để)
Câu 1:<4 đ>Tìm hai số $x,y$ nguyên thoả mãn $x^2-xy=7x-2y-15$
Câu 2:<3 đ>
Giải hệ phương trình:
$\left\{\begin{matrix}\frac{x}{x^2+1}+\frac{y}{y^2+1}=\frac{2}{3}\\ (x+y)(1+\frac{1}{xy})=6\end{matrix}\right.$
Câu 3:<5 đ>
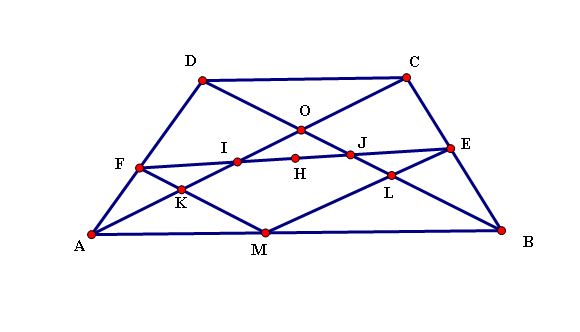
Cho hình thang $ABCD(AB//CD)$. Trên đáy lớn AB lấy điểm M không trùng với các đỉnh. Qua M kẻ các đường thẳng song song với AC và BD, các đường thẳng này cắt hai cạch BC, AD lần lượt tại E và F. Đoạn EF cắt AC và BD lần lượt tại I và J. Gọi H là trung điểm của IJ.
a. Chứng minh rằng: $FH=HE$
b. Cho $AB=2CD$. Chứng minh rằng: $EJ=JI=IF$
Câu 4:<3 đ>
Cho đường tròn O và một dây cung $AB(O\not\in AB)$. Các tiếp tuyến tại A và B của đường tròn cắt nhau tại C. Kẻ dây cung CD của đường tròn đường kính $OC(D\neq A,B)$. Dây cung CD cắt cung AB của đường tròn (O) tại E (E nằm giữa C và D).
a. Chứng minh: $\widehat{BED}=\widehat{DAE}$
b. Chứng minh: $DE^2=DA.DB$
Câu 5:<2 đ>
Cho $S=\frac{1}{\sqrt{1.2012}}+\frac{1}{\sqrt{2.2011}}+...+\frac{1}{\sqrt{k(2012-k+1)}}+...+\frac{1}{\sqrt{2012.1}}, (k\in \mathbb{N};1\leq k\leq 2012)$
So sánh S và $\frac{4024}{2013}$
Câu 6:<3 đ>
Cho $x,y,z$ là ba số dương thoả mãn $xyz=1.$
Chứng minh rằng:$\frac{x^2}{y+1}+\frac{y^2}{z+1}+\frac{z^2}{x+1}\geq \frac{3}{2}$
Bỏ hai bài hình............. Đời ta coi như xuống dốc
Bài viết đã được chỉnh sửa nội dung bởi minhtuyb: 03-03-2012 - 16:16