Chủ đề này có 32 trả lời

[E. Galois]

Chuyển nhanh đến:
1) Điều lệ
2) Đăng kí thi đấu
3) Lịch thi đấu và tổng hợp kết quả

BTC yêu cầu MSS09 ra đề vào topic này. Sau khi đánh máy đề, phải nhấn nút Chấp nhận để để được hiện lên.

Các toán thủ khi thi đấu, cứ yên tâm rằng, sau khi trả lời là bài làm đã được lưu, BTC đã nhận được bài làm của bạn, có điều bạn không nhìn thấy được mà thôi. Bạn nên mừng vì điều này, như thế các toán thủ khác không thể copy bài của bạn được.

Bạn cũng nên sử dụng chức năng xem trước của diễn đàn để sửa các lỗi Latex trước khi gửi bài, vì gửi rồi sẽ không xem và sửa lại được nữa

b. Luật Loại trực tiếp: Luật chỉ áp dụng khi có $n >20$ toán thủ tham gia thi đấu.
- Sau mỗi trận, $k$ toán thủ có số điểm ít nhất sẽ bị loại. Trong trường hợp có nhiều toán thủ cùng điểm số, toán thủ nào có thời gian bỏ thi đấu dài nhất sẽ ưu tiên bị loại.
$$k=\frac{\left \{(n-10) - [(n-10) \mod 10] \right \}}{10}$$
- Toán thủ bị loại sẽ không đuợc đăng kí lại
- Khi Chỉ còn 20 toán thủ, Luật này ko còn hiệu lực

BTC lưu ý:
1) trận 8 có 31 toán thủ tham gia nên sau trận này, 02 toán thủ ít điểm nhất sẽ bị loại.

2) Các toán thủ chớ quên rằng mỗi một mở rộng đúng sẽ được 10 điểm, các bạn nên mở rộng bài toán để thu được nhiều điểm hơn

[minhtuyb]

Đêm nay anh Thế unhide đề hộ em nhé

Đề của MSS09:
Cho tam giác $ABC$ có các đường trung tuyến xuất phát tại đỉnh B và C vuông góc với nhau. Tìm GTNN của biểu thức:
$S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2}$

[WhjteShadow]

Đây là lời giải còn hình em sẽ up lên sau(em chưa biết vẽ T.T):
Vẽ đường trung tuyến xuất phát từ B và C lần lượt là BN và CM (M nằm giữa A và B,N nằm giữa A và C) và BN cắt CM tại O
TA có do MN là đường trung bình của tam giác ABC $\Rightarrow MN=\dfrac{1}{2}BC$ và $MN \parallel BC$
Theo Ta-let có $\dfrac{OM}{OC}=\dfrac{ON}{OB}=\dfrac{1}{2}$
Đặt $OM=a,ON=b \Rightarrow OC=2a,OB=2b$
Mà do $BN\perp CM$ nên theo Pythago có $OM^2+OB^2=BM^2;ON^2+OC^2=NC^2;OB^2+OC^2=BC^2$
Hay $a^2+4b^2=BM^2;b^2+4a^2=NC^2;4a^2+4b^2=BC^2 \Rightarrow 5a^2+5b^2=BM^2+CN^2$
Nhưng do $AM=\dfrac{1}{2}AB$ và $AN=\dfrac{1}{2}AC \Rightarrow 20a^2+20b^2=AB^2+AC^2=5BC^2$
Vậy $AB^2+AC^2=5BC^2$
Vẽ AH vuông góc với BC tại H $\Rightarrow \sin^2 ABC=\dfrac{AH^2}{AB^2}; \sin^2 ACB=\dfrac{AH^2}{AC^2}$

Ta sẽ chứng minh $\dfrac{1}{\sin^2 ABC}+\dfrac{1}{\sin^2 ACB}\geq \dfrac{20}{9}$
$\Leftrightarrow \dfrac{AB^2+AC^2}{AH^2}\geq \dfrac{20}{9}$
$\Leftrightarrow 9(AB^2+AC^2)\geq 20AH^2$
$\Leftrightarrow 18AH^2+9(BH^2+CH^2)\geq 20AH^2$ (Theo pythago với 2 tam giác vuông ABH và ACH)
$\Leftrightarrow 9(BH^2+CH^2)\geq 2AH^2$
$\Leftrightarrow 10(BH^2+CH^2)\geq (AH^2+BH^2)+(AH^2+CH^2)$
$\Leftrightarrow 10(BH^2+CH^2)\geq AB^2+AC^2$ (Theo Pythago)
$\Leftrightarrow 10(BH^2+CH^2)\geq 5BC^2$ (Do$AB^2+AC^2=5BC^2$)
$\Leftrightarrow 2(BH^2+CH^2)\geq BC^2$
$\Leftrightarrow BH^2+CH^2 \geq 2BH.CH$ (Luôn đúng theo BĐT Cauchy)
$\Rightarrow \dfrac{\sqrt 3}{\sin^2 ABC}+\dfrac{\sqrt 3}{\sin^2 ACB}+\sqrt 2 \geq \dfrac{\sqrt 3 .9}{20}+\sqrt 2$
Dấu "=" xảy ra $\Leftrightarrow \vartriangle ABC$ cân tại A và $AC=AB=\sqrt{\dfrac{5}{2}}BC$
Mở rộng:
do $\dfrac{1}{\sin^2 ABC}+\dfrac{1}{\sin^2 ACB} \geq \dfrac{20}{9}$
Và áp dụng bđt $\dfrac{x^n+y^n}{2}\geq \left( {\frac{{x + y}}{2}} \right)^n$
ta sẽ có hướng mở rộng là c/m $\frac{{x^{2n} + y^{2n} }}{2} \ge \left( {\frac{{10}}{9}} \right)^n$
Mở rộng 2 của WhjteShadow: Đặt $\frac{1}{sinABC}=a$,$\frac{1}{sinABC}=b$
$\Rightarrow a^2+b^2\geq\frac{20}{9}$
Ta sẽ Khai thác từ $a^{2n}+b^{2n}\geq (\frac{10}{9})^n.2$
Theo BĐT Bunyakoski ta có
\[
\Rightarrow (a^{3n} + b^{3n} )(a^n + b^n ) \ge (a^{2n} + b^{2n} )^2 \ge \left[ {\left( {\frac{{10}}{9}} \right)^n .2} \right]^2
\]
Hay đề mở rộng là c/m
\[
(\frac{1}{{sin^n ABC}} + \frac{1}{{sin^n ACB}})(\frac{1}{{sin^{3n} ABC}} + \frac{1}{{sin^{3n} ACB}}) \ge \left[ {\left( {\frac{{10}}{9}} \right)^n .2} \right]^2
\]


Mong em gõ latex thuần thục hơn chút. Lời giải tốt. Thuần túy hình học.
D-B=11.4h
E=10
F=2 * 10=20
S=86.6

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 11-04-2012 - 21:24

[nthoangcute]

Bài này khá hay:
Bổ đề 1: Cho $\Delta$ABC, đặt $\widehat{BAC}=\delta$, $BC=a,CA=b,AB=c$. Khi ấy: $\frac{1}{sin(\delta)}=\frac{bc}{2S_{ABC}}$
Chứng minh bổ đề 1:
Xét $\delta < 90^o$: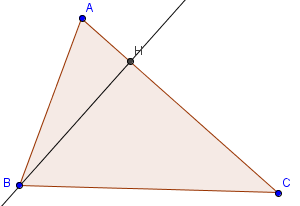

Lúc đó, ta kẻ đường cao BH của $\Delta$ABC. Vậy $S_{ABC}=\frac{BH.AC}{2}=\frac{BH.b}{2}$ (1)
Lại có $\Delta$ABH vuông tại H nên $sin(\delta)=\frac{BH}{AB}=\frac{BH}{c}$ (2)
Từ (1), (2) $\to \frac{1}{sin(\delta)}=\frac{bc}{2S'_{ABC}}$
Xét $\delta = 90^o$:
Khi đó $\Delta$ABC vuông tại H. Vậy $sin(\delta)=sin(90^o)=1$ và $S'_{ABC}=\frac{bc}{2}$
$\to \frac{1}{sin(\delta)}=\frac{bc}{2S_{ABC}}$
Xét $\delta > 90^o$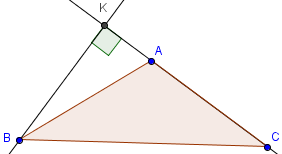

Kẻ đường cao BK của $\Delta$ABC. Vậy $S_{ABC}=\frac{BK.AC}{2}=\frac{BK.b}{2}$ (3)

Lại có $\Delta$ABK vuông tại K nên $sin(\delta)=sin(180^o-\delta)=sinBAK=\frac{BK}{AB}=\frac{BK}{c}$ (4)

Từ (3), (4) $\to \frac{1}{sin(\delta)}=\frac{bc}{2S_{ABC}}$

Tóm lại, Bổ đề 1 được Chứng minh.
Bổ đề 2: Cho $\Delta$ABC, trung tuyến $AM=m_a$. Đặt $BC=a,CA=b,AB=c$ ($a,b,c>0$). Khi ấy: $4m_a^2+a^2=2(b^2+c^2)$
(Bổ đề này quá quen thuộc nên mình xin phép không chứng minh, nếu cần chúng minh cứ hỏi mình)

Bổ đề 3: Cho $\Delta$ABC. Đặt $BC=a,CA=b,AB=c$ ($a,b,c>0$). Đặt diện tích $\Delta$ABC=S'.
Khi ấy: $16S'^2=4(a^2b^2+b^2c^2+c^2a^2)-(a^2+b^2+c^2)^2$
Chứng minh bổ đề 3:
Ta có $16S'=16p(p-a)(p-b)(p-c)$ (với p là nửa chu vi $\Delta$ABC)

$=(a+b+c)(a+b-c)(b+c-a)(c+a-b)$

$=2(a^2b^2+b^2c^2+c^2a^2)-a^4-b^4-c^4$

$=4(a^2b^2+b^2c^2+c^2a^2)-(a^2+b^2+c^2)^2$ (đpcm)
Trở lại với bài toán: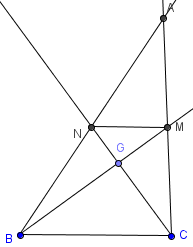

Kẻ đường trung tuyến BM, CN của $\Delta$ABC cắt nhau tại G. Đặt $BC=a,CA=b,AB=c$ ($a,b,c>0$).
Gọi $\widehat{ABC}=\alpha$, $\widehat{ACB}=\beta$. Đặt diện tích $\Delta$ABC=S'.
Vậy G là trọng tâm $\Delta$ABC hay $\frac{BG}{BM}=\frac{CG}{CM}=\frac{2}{3}$
Áp dụng Bổ đề 2 ta có:
$4BM^2+b^2=2(a^2+c^2)$

$4CN^2+c^2=2(a^2+b^2)$

$\to 4BM^2+4CN^2+b^2+c^2=4a^2+2b^2+2c^2$

$\to 4(\frac{3BG}{2})^2+4(\frac{3CG}{2})^2=4a^2+b^2+c^2$

$\to 9(BG^2+CG^2)=4a^2+b^2+c^2$

Lại thấy $\Delta$BGC vuông tại G nên $BG^2+CG^2=a^2$

$\to 9a^2=4a^2+b^2+c^2$

$\to 5a^2=b^2+c^2$

Ta thấy:
Áp dụng Bổ đề 1 thì $\frac{1}{sin(\alpha)}=\frac{ac}{2S'}$ và $\frac{1}{sin(\beta)}=\frac{ab}{2S'}$

suy ra $\frac{1}{sin^2(\alpha)}+\frac{1}{sin^2(\beta)}$

$=\frac{a^2b^2+a^2c^2}{4S'^2}$

$=\frac{4a^2(b^2+c^2)}{16S'^2}$

$=\frac{4a^2.5a^2}{4(a^2b^2+b^2c^2+c^2a^2)-(a^2+b^2+c^2)^2}$

$=\frac{20a^4}{4(a^2(b^2+c^2)+b^2c^2)-(6a^2)^2}$

$=\frac{20a^4}{4b^2c^2-16a^4}$

$=\frac{5a^4}{b^2c^2-4a^4}$

Ta có: áp dụng BĐT cô-si cho 2 số dương thì:
$bc \leq \frac{b^2+c^2}{2}=\frac{5a^2}{2}$

Khi đó: $\frac{5a^4}{b^2c^2-4a^4} \geq \frac{5a^4}{(\frac{5a^2}{2})^2-4a^4}=\frac{20}{9}$

Vậy: $\frac{1}{sin^2(\alpha)}+\frac{1}{sin^2(\beta)} \geq \frac{20}{9}$
suy ra:
$S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2}$

$=\sqrt{3}.(\frac{1}{sin^2(\alpha)}+\frac{1}{sin^2(\beta)})+\sqrt{2}$

$\geq \frac{20 \sqrt{3}}{9}+\sqrt{2}$

$=\frac{20\sqrt{3}+9\sqrt{2}}{9}$

Vậy $S_{min}=\frac{20\sqrt{3}+9\sqrt{2}}{9} \Leftrightarrow b=c=\frac{\sqrt{10}a}{2} \Leftrightarrow \Delta$ABC cân tại A có $AC=AB=\frac{\sqrt{10}BC}{2}$
__________________________________________________________________________
Mở rộng đây:
Đặt $BC=a,CA=b,AB=c$ ($a,b,c>0$).
Gọi $\widehat{ABC}=\alpha$, $\widehat{ACB}=\beta$., $\widehat{CAB}=\gamma$
Đặt diện tích $\Delta$ABC=S.
Với đề bài như vậy, ta có thể:

1. Tìm Min của $A=\frac{1}{sin^{2n} \alpha}+\frac{1}{sin^{2n} \beta}$ ($n \in N^*$)

2. Tìm Max của $B=sin^{2n} \alpha+sin^{2n} \beta$ ($n \in N^*$)

3. Tìm Min của $C=\frac{1}{sin^{2n} \alpha}+\frac{1}{sin^{2n} \beta}+\frac{1}{sin^{2n} \gamma}$ ($n \in N^*$)


Chứng minh các mở rộng:
Với cách làm tương tự của bài toán gốc, ta có:
Đặt $sin(\alpha) =x, sin(\beta) =y, sin( \gamma)=z$
Khi ấy: $\frac{1}{x^2}+\frac{1}{y^2} \geq \frac{20}{9}$
1. $A=\frac{1}{sin^{2n} \alpha}+\frac{1}{sin^{2n} \beta} $

$=\frac{1}{x^{2n}}+\frac{1}{y^{2n}}$

Áp dụng BĐT cô si :
$\frac{\frac{1}{x^{2n}}+\frac{1}{y^{2n}}}{2} \geq (\frac{\frac{1}{x^2}+\frac{1}{y^2}}{2})^n \geq (\frac{10}{9})^n$

Hay $A=\frac{1}{x^{2n}}+\frac{1}{y^{2n}} \geq \frac{10^n}{2.9^n}$

Suy ra ...
2. Áp dụng kết quả của bài toán gốc thì:
$sin^2(\alpha)+sin^2(\beta)$

$=\frac{4S^2}{a^2b^2}+\frac{4S^2}{a^2c^2}$

$=\frac{4S^2.(b^2+c^2)}{a^2b^2c^2}$

$=\frac{20S^2}{b^2c^2}$

Lại có: theo bài toán gốc thì ta đã CM được $4S=b^2c^2-4a^4$

Do đó $sin^2(\alpha)+sin^2(\beta)$

$=\frac{5(b^2c^2-4a^4)}{b^2c^2}$

$\leq \frac{5.(b^2c^2-4.\frac{4b^2c^2}{25})}{b^2c^2}$

$=\frac{9}{5}$

Vậy:...
"Chú ý: có thể sử dụng BĐT này để Tìm Min của Bài toán gốc bằng BĐT: $\frac{1}{m}+\frac{1}{n} \geq \frac{4}{m+n}$"
3. (Cái này khó hơn)
Cũng sử dụng kết quả của bài toán gốc để có:

$C'=\frac{1}{sin^{2} \alpha}+\frac{1}{sin^{2} \beta}+\frac{1}{sin^{2} \gamma}$

$=\frac{a^2b^2}{4S^2}+\frac{b^2c^2}{4S^2}+\frac{c^2a^2}{4S^2}$

$=\frac{a^2b^2+b^2c^2+c^2a^2}{4S^2}$

$=\frac{4(a^2b^2+b^2c^2+c^2a^2)}{4(a^2b^2+b^2c^2+c^2a^2)-(a^2+b^2+c^2)^2}$

$=\frac{4}{4-\frac{(a^2+b^2+c^2)^2}{a^2b^2+b^2c^2+c^2a^2}}$

$=\frac{4}{4-\frac{(6a^2)^2}{5a^4+b^2c^2}}$

$\geq \frac{4}{4-\frac{36a^4}{5a^4+\frac{25a^4}{4}}}$

$=5$
Áp dụng BĐT: $\frac{x^n+y^n+z^n}{3} \geq (\frac{x+y+z}{3})^n$, ta được:
$C=\frac{1}{sin^{2n} \alpha}+\frac{1}{sin^{2n} \beta}+\frac{1}{sin^{2n} \gamma}$
$\geq 3.(\frac{\frac{1}{sin^{2} \alpha}+\frac{1}{sin^{2} \beta}+\frac{1}{sin^{2} \gamma}}{3})^n$
$\geq 3.(\frac{5}{3})^n$

Lời giải tốt, tuy khá nặng. Bỏ qua các lỗi lặt vặt không đáng kể.
D-B=12.9h
E=9.9
F=3 * 10=30
S=94.8

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 11-04-2012 - 20:52

[phantomladyvskaitokid]

Gọi G là giao của 2 đường trung tuyến BD và CE thì G là trọng tâm tam giác ABC

tam giác ABC có D, E là trung điểm của AC, AB nên DE//BC

Gọi I, N, K là chân đường vuông góc hạ từ E, G, D xuống BC, H là trung điểm của BC

kéo dài NG cắt ED tại M

do DE//BC nên EI=DK=MN

$\Delta GNC$ có EM//NC $\Rightarrow \frac{MG}{MN}=\frac{EG}{EC}=\frac{2}{3}\Rightarrow MN=\frac{2}{3}GN$ X

theo quan hệ đường vuông góc, đường xiên $GN\leq GH$

tam giác GBC vuông ở G có trung tuyến GH nên $GH=\frac{1}{2}BC$

do đó$EI=DK\leq \frac{1}{2}BC$

a/d định lí pytago ta có $BE^2+DC^2=EG^2+BG^2+DG^2+GC^2=\frac{5}{4}(GB^2+GC^2)=\frac{5}{4}BC^2$

ta có

$S=\sqrt{3}(\frac{BE^2}{EI^2}+\frac{DC^2}{DK^2})+\sqrt{2}=\sqrt{3}\frac{BE^2+CD^2}{EI^2}+\sqrt{2}\geq \sqrt{3}\frac{\frac{5}{4}BC^2}{\frac{1}{4}BC^2}+\sqrt{2}=5\sqrt{3}+\sqrt{2}$

dấu = xảy ra khi và chỉ khi tam giác ABC có $AB=AC=\frac{\sqrt{10}}{2}BC$

Sai từ dấu X trở xuống dẫn đến sai kết quả. Vẫn cho điểm nửa đoạn trên.
D-B=17.9h
E=4
F=0
S=42.1

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 11-04-2012 - 20:59

[NLT]

BN,CM là các trung tuyến, AD, GH lần lượt vuông góc BC tại G, H => G là trọng tâm tam giác ABC.

$S = \frac{{\sqrt 3 }}{{\frac{{AD^2 }}{{AB^2 }}}} + \frac{{\sqrt 3 }}{{\frac{{AD^2 }}{{AC^2 }}}} + \sqrt 2 $

$ = \,\frac{{\sqrt 3 \left( {AB^2 + AC^2 } \right)}}{{AD^2 }} + \sqrt 2 $

Bây giờ ta chứng minh $AB^2 + AC^2 = 5BC^2 $
Xét tam giác BGC, ta có\[BC^2 = BG^2 + GC^2 = 4\left( {GM^2 + GN^2 } \right)\]
Xét tam giác BGM, ta có : \[BM^2 = BG^2 + GM^2 \to \frac{{AB^2 }}{4} = GM^2 + 4GN^2 \]
Xét tam giác CGN, ta có : \[CN^2 = CG^2 + GN^2 \to \frac{{AC^2 }}{4} = 4GM^2 + GN^2 \]
Suy ra:\[\frac{{AB^2 + AC^2 }}{4} = 5\left( {GM^2 + GN^2 } \right) = \frac{5}{4}BC^2 \]

\[ \to AB^2 + AC^2 = 5BC^2 \]

Do đó: \[S = \frac{{\sqrt 3 \left( {AB^2 + AC^2 } \right)}}{{AD^2 }} + \sqrt 2 = \frac{{5\sqrt 3 BC^2 }}{{AD^2 }} + \sqrt 2 \]

Mặt khác: \[\frac{{BC}}{{AD}} = \frac{{BC}}{{3GH}} \ge \frac{{2GH}}{{3GH}} = \frac{2}{3}\]
(Theo Thales ta suy ra AD=3GH)
Vì vậy, \[S \ge \frac{{20\sqrt 3 }}{9} + \sqrt 2 \]
Vậy Min S=\[\frac{{20\sqrt 3 }}{9} + \sqrt 2 \] khi BC=2GH => Tam giác ABC cân tại A

Lời giải chưa chặt ở phần dấu =.
D-B=20.2h
E=9
F=0
S=54.8

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 11-04-2012 - 21:15

[Nguyễn Hữu Huy]

Đêm nay anh Thế unhide đề hộ em nhé

Đề của MSS09:
Cho tam giác $ABC$ có các đường trung tuyến xuất phát tại đỉnh B và C vuông góc với nhau. Tìm GTNN của biểu thức:
$S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2}$

Ta dễ dàng thấy đc tam giác trên chỉ có thể nằm ở các dạng sau :
Dạng 1 : Tam giác nhọn

Dạng 2 : Tam giác có góc B hoặc góc C tù (TH 2 xin được post sau )

TH 1 : Đối với tam giác nhọn !
Gọi đường trung tuyến CN và BM ; ; gọi G là trọng tâm ; AG cắt BC tại D
Kẻ đường cao AH vuông góc với BC


Ta có
$sin^2 \widehat{ABC} = \dfrac{AH^2}{AB^2} \Rightarrow \dfrac{1}{sin^2 \widehat{ABC}} = \dfrac{AB^2}{AH^2}$

$sin^2 \widehat{ACB} = \dfrac{AH^2}{AC^2} \Rightarrow \dfrac{1}{sin^2 \widehat{ACB}} = \dfrac{AC^2}{AH^2}$

KHi đó

$\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB} = \frac{\sqrt{3}.(AB^2 + AC^2)}{AH^2} = \frac{\sqrt{3}.(2AH^2 + BH^2 + CH^2)}{AH^2} = 2.\sqrt{3} + \frac{\sqrt{3}.(BH^2 + CH^2)}{AH^2}$ (*1)

(đúng theo định lý Pitago : $AB^2 + AC^2 = AH^2 + BH^2 + AH^2 + CH^2 = 2AH^2 + BH^2 + CH^2$)

Theo BĐT AM - GM thì ta có
$BH^2 + CH^2 \geq \dfrac{(BH + CH)^2}{2} = \dfrac{BC^2}{2}$ (1)

Từ gt ta có :
2 đường trung tuyến BM và CN vuông góc với nhau
Gọi G là trọng tâm tam giác ABC
Gọi giao của AG cắt BC tại D
$\Rightarrow$ D là trung điểm BC
$\Rightarrow GD = \dfrac{1}{2}BC $ (do GD là đg trung tuyến ứng vs cạnh huyền của tam giác BGC vuông tại G)

mà $AD = 3GD$ ( do AD là đường trung tuyến , G là trọng tâm )

$\Rightarrow AD = \dfrac{3}{2}.BC$
Mà $AD \geq AH \Rightarrow \dfrac{3}{2}.BC \geq AH \Rightarrow \dfrac{9}{4}.BC^2 \geq AH^2 $ (2)

Từ (1) và (2)
$ \Rightarrow \frac{\sqrt{3}.(BH^2 + CH^2)}{AH^2} \geq \frac{\sqrt{3}.(\dfrac{BC^2}{2})}{\dfrac{9}{4}.BC^2} = \dfrac{2\sqrt{3}}{9} $ (*2)

Từ (*1) và (*2) ta có
$S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2} = \sqrt{2} + 2\sqrt{3} + \dfrac{2\sqrt{3}}{9} $

Dấu "=" xảy ra khi và chỉ khi tam giác ABC cân !

p/s : Có cần tìm đk gì nữa ko nhỉ !!? Xin được nợ hình BCT - em xin post sau (máy em bị lỗi ko vẽ đc)

Đêm nay anh Thế unhide đề hộ em nhé

Đề của MSS09:
Cho tam giác $ABC$ có các đường trung tuyến xuất phát tại đỉnh B và C vuông góc với nhau. Tìm GTNN của biểu thức:
$S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2}$

Bổ sung cho dấu "=" xảy ra ở TH 1

Dấu "=" xảy ra $\Leftrightarrow BH = CH$ ; AD vuông góc với BC

${\color{Blue} \Leftrightarrow }$ Tam giác ABC cân tại A

TH 2 :
Ở Th này , ta có 1 trong hai góc B hoặc C tù
Không mất tính tổng quát , giả sử $\widehat{B} \geq 90^0 > \widehat{C}$



Khi đó ta cũng thực hiện tương tự TH 1 , vẻ đường cao AH vuông góc với B
Tương tự TH 1
Ta cũng tìm ra được

$\frac{\sqrt{3}}{sin^2 \widehat{ABC}} + \frac{\sqrt{3}}{sin^2 \widehat{ACB}}$

$= \dfrac{\sqrt{3}.AB^2}{AH^2} + \dfrac{\sqrt{3}.AC^2}{AH^2}$ (ở đoạn này thì sử dụng t/c 2 bù nhau thì có tỷ số lượng giác bằng nhau ; $\widehat{ABC} + \widehat{ABH} = 180^0 \Rightarrow Sin^2 \widehat{ABC} = Sin^2 \widehat{ABH}$
p/s : Có cần chứng minh ko nhỉ !?)

$= \dfrac{\sqrt{3}.(AB^2 + AC^2)}{AH^2} $

$= \dfrac{\sqrt{3}.(AH^2 + HB^2 + AH^2 + HC^2) }{AH^2}$ (áp dụng Pi-Ta-Go với 2 tam giác ABH và ACH cùng vuông ở H)

$= \dfrac{\sqrt{3}.(2AH^2 + HB^2 + HC^2)}{AH^2}$

$= 2\sqrt{3} + \dfrac{\sqrt{3}.(BH^2 + CH^2}{AH^2}$

Mặt khác khí đó nếu nhìn kĩ thì ta sẽ thấy

$BH^2 + CH^2 \geq \dfrac{(BH + CH)^2}{2} > BC^2 > \dfrac{BC^2}{2}$ (theo AM- GM)

Và Mặt khác cũng có $AH^2 \leq \dfrac{9}{4}BC^2$ (từ TH 1)

KHi đó
$2\sqrt{3} + \dfrac{\sqrt{3}.(BH^2 + CH^2)}{AH^2} > 2\sqrt{3} + \dfrac{\sqrt{3}.\frac{BC^2}{2}}{\dfrac{9}{4}BC^2} > 2\sqrt{3} + \dfrac{2\sqrt{3}}{9}$

$\Rightarrow S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2}> 2\sqrt{3} + \dfrac{2\sqrt{3}}{9} + \sqrt{2}$


Từ TH1 và TH2 ta thấy rằng $Min S = \frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2} = 2\sqrt{3} + \dfrac{2\sqrt{3}}{9} + \sqrt{2}$

Min xảy ra ở TH1 (tam giác ABC nhọn)

Dấu "=" xảy ra ở TH 1

Dấu "=" xảy ra $\Leftrightarrow BH = CH$ ; AD vuông góc với BC

${\color{Blue} \Leftrightarrow }$ Tam giác ABC cân tại A

Đêm nay anh Thế unhide đề hộ em nhé

Đề của MSS09:
Cho tam giác $ABC$ có các đường trung tuyến xuất phát tại đỉnh B và C vuông góc với nhau. Tìm GTNN của biểu thức:
$S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2}$

Mở rộng cho bài trên
Nếu thay đổi giữ kiện sin thành cos hoặc tan thì bài toán có thay đổi chút ít
Xin được bỏ đi lượng $\sqrt{2}$ ko cần thiết

$S=\frac{\sqrt{3}}{tan^2ABC}+\frac{\sqrt{3}}{tan^2ACB}$
Thực hiện các bước biến đổi tương tự như bài toán gốc
Ta có
$S=\frac{\sqrt{3}}{tan^2ABC}+\frac{\sqrt{3}}{tan^2ACB}$

$S = \dfrac{\sqrt{3}(BH^2 + CH^2)}{AH^2}$ (*)

và tới đây , 1 cách tự nhiên ta sẽ nghĩ tới việc "nguy trang" bài toán
Chứng minh rằng
$\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB} \geq \frac{\sqrt{3}}{tan^2ABC}+\frac{\sqrt{3}}{tan^2ACB}$

Ko mấy khó khăn để chứng mih điều trên (từ bài toán gốc và (*))

Nhưng nếu thấy việc "ngụy trang" trên chưa đủ
Thì tiếp tục dùng CT
$sin^2 a + cos^2 a = 1$
Thay $cos^2 a = 1 - sin^2 a$

Khi đó ta có bài toán

Chứng minh rằng
$\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB} \geq \frac{\sqrt{3}}{1 - sin^2ABC}+\frac{\sqrt{3}}{1 - sin^2ACB}$
(cũng ko ngụy trang được là bao hì !?)

Cũng có 1 ý tưởng khác nhưng chắc em phá sản
Thay $sin^2 ABC$ bằng $Cos^2 ABC$
Cũng ko biết nó có min hay ko !?

Về mở rộng thì rất nhiều (mở kho BĐT lượng giác là ta có thể mở ra 1 lượng lớn bài toán mở rộng hay)
VD
dùng BĐT
sin A + sin B + sic C \leq \frac{3\sqrt{3}}{2}

ta sẽ chế đc
Tìm Min
$\frac{1}{sin^2 A} + \frac{1}{sin^2 B} + \frac{1}{sin^2 C} \geq \frac{9}{sin^2 A + sin^2 B + sin^2 C} \geq \frac{9}{\frac{(sin A + sin B + sin C)^2}{3}} \geq \frac{9}{\frac{27}{4}} = \frac{4}{3}$

Và nhiều mở rộng đóng hẹp khác!

P/s : Quên ! Do 2 góc hợp bởi 2 đg trung tuyến xuất phát ở B và C của tam giác ABC nên góc A < 90*
nên chỉ có 2 TH đã xét (ko "truy sát" TH này vì nó dễ thấy (nhưng sợ anh Hân lắm nên cứ viết vô đc bao nhiều hay bấy nhiêu ! anh Hân hầy ! hjhjhj)

Lý luận dấu = chưa chặt. Các bài "chế" chưa thực sự hay. Mở rộng 3 không tính.
D-B=21.2h
E=9
F=2 * 10=20
S=73.8

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 11-04-2012 - 21:22

[Dung Dang Do]

Giải:
Gọi $E,F$ là trung điểm của $AC$ và $AB$. Hạ đường cao AH ta có
$$sin^2 ABC=\frac{AH^2}{AB^2}$$
$$sin^2 ACB=\frac{AH^2}{AC^2}$$
Thay vào biểu thức $S$ ta có
$$S=\frac{\sqrt{3}(AB^2+AC^2)}{AH^2}+\sqrt{2}$$
Mà $AH<AD$ X (quan hệ đường xiên và hình chiếu)
$$\to S \ge \frac{\sqrt{3}(AB^2+AC^2)}{AD^2}+\sqrt{2}$$
Ta lại có:$AD=3GD;BC=2GD \iff AD=\frac{3}{2}BC<1>$
Dễ thấy $GD=\frac{1}{2}BC=>AD^2=\frac{9}{4}BC^2$
$BG^2+GF^2=BF^2=\frac{1}{4}AB^2$
(định lý Pytago)
$$BG^2+GF^2=BF^2=\frac{1}{4}AB^2$$
mà $$BF=\frac{1}{2}CG; GE=\frac{1}{2}BG$$
$$\iff 4BG^2+CG^2=AB^2;4CG^2+BG^2=AC^2$$
$$\iff 5(BG^2+CG^2)=AB^2+AC^2$$
$$ 5BC^2=AB^2+AC^2<2>$$
Từ $<1><2>$ ta có
$$S \ge \frac{\sqrt{3}*BC^2}{\frac{9}{4}BC^2}+\sqrt{2}=\sqrt{3}*\frac{20}{9}+\sqrt{2}$$
Dấu bằng xảy ra khi và chỉ khi $$AH=AD \iff H \equiv D$$
Vậy $$Min S=\sqrt{3}*\frac{20}{9}+\sqrt{2}\iff AH=AD \iff H \equiv D$$

Lý luận dấu = chưa chặt.
D-B=22h
E=8.5
F=0
S=51.5

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 11-04-2012 - 21:16

[E. Galois]

Trận đấu đã kết thúc, đây là lúc minhtuyb nêu đáp án và các toán thủ chém gió về bài làm của nhau

[nthoangcute]

Mở rộng 2 của WhjteShadow: Đặt $\frac{1}{sinABC}=a$,$\frac{1}{sinABC}=b$
=>$a^2+b^2=\frac{20}{9}$ Ta sẽ Khai thác từ $a^{2n}+b^{2n}\geq (\frac{10}{9})^n.2$ Và Bunhia ta có
=>$(a^{3n}+b^{3n})(a^{n}+b^{n})\geq (a^{2n}+b^{2n})^2\geq [(\frac{10}{9})^n.2]}^2$
Hay đề mở rộng là c/m $(\frac{1}{sin^nABC}+\frac{1}{sin^nACB})(\frac{1}{sin^{3n}ABC}+\frac{1}{sin^{3n}ACB})\geq [(\frac{10}{9})^n.2]^2$
(các a m0d ơi nếu có lỗi latex thì sửa hộ e với nha

sai rùi Đạt ơi:
>$a^2+b^2 \geq \frac{20}{9}$ chứ

Bài viết đã được chỉnh sửa nội dung bởi nthoangcute: 09-04-2012 - 12:32

[WhjteShadow]

HI lúc đấy mẹ cứ giục đi ngủ nên nhầm @@~.Ánh ơi xem lại đi kết quả sai rồi kìa

[minhtuyb]

Bổ sung cho dấu "=" xảy ra ở TH 1

Dấu "=" xảy ra $\Leftrightarrow BH = CH$ ; AD vuông góc với BC

${\color{Blue} \Leftrightarrow }$ Tam giác ABC cân tại A

TH 2 :
Ở Th này , ta có 1 trong hai góc B hoặc C tù
Không mất tính tổng quát , giả sử $\widehat{B} \geq 90^0 > \widehat{C}$



Khi đó ta cũng thực hiện tương tự TH 1 , vẻ đường cao AH vuông góc với B
Tương tự TH 1
Ta cũng tìm ra được

$\frac{\sqrt{3}}{sin^2 \widehat{ABC}} + \frac{\sqrt{3}}{sin^2 \widehat{ACB}}$

$= \dfrac{\sqrt{3}.AB^2}{AH^2} + \dfrac{\sqrt{3}.AC^2}{AH^2}$ (ở đoạn này thì sử dụng t/c 2 bù nhau thì có tỷ số lượng giác bằng nhau ; $\widehat{ABC} + \widehat{ABH} = 180^0 \Rightarrow Sin^2 \widehat{ABC} = Sin^2 \widehat{ABH}$
p/s : Có cần chứng minh ko nhỉ !?)

$= \dfrac{\sqrt{3}.(AB^2 + AC^2)}{AH^2} $

$= \dfrac{\sqrt{3}.(AH^2 + HB^2 + AH^2 + HC^2) }{AH^2}$ (áp dụng Pi-Ta-Go với 2 tam giác ABH và ACH cùng vuông ở H)

$= \dfrac{\sqrt{3}.(2AH^2 + HB^2 + HC^2)}{AH^2}$

$= 2\sqrt{3} + \dfrac{\sqrt{3}.(BH^2 + CH^2}{AH^2}$

Mặt khác khí đó nếu nhìn kĩ thì ta sẽ thấy

$BH^2 + CH^2 \geq \dfrac{(BH + CH)^2}{2} > BC^2 > \dfrac{BC^2}{2}$ (theo AM- GM)

Và Mặt khác cũng có $AH^2 \leq \dfrac{9}{4}BC^2$ (từ TH 1)

KHi đó
$2\sqrt{3} + \dfrac{\sqrt{3}.(BH^2 + CH^2)}{AH^2} > 2\sqrt{3} + \dfrac{\sqrt{3}.\frac{BC^2}{2}}{\dfrac{9}{4}BC^2} > 2\sqrt{3} + \dfrac{2\sqrt{3}}{9}$

$\Rightarrow S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2}> 2\sqrt{3} + \dfrac{2\sqrt{3}}{9} + \sqrt{2}$


Từ TH1 và TH2 ta thấy rằng $Min S = \frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2} = 2\sqrt{3} + \dfrac{2\sqrt{3}}{9} + \sqrt{2}$

Min xảy ra ở TH1 (tam giác ABC nhọn)

Dấu "=" xảy ra ở TH 1

Dấu "=" xảy ra $\Leftrightarrow BH = CH$ ; AD vuông góc với BC

${\color{Blue} \Leftrightarrow }$ Tam giác ABC cân tại A

Các bạn đều thiếu TH này thì phải
Đáp án mình có TH này
P/s: Trâu bò quá, tưởng leo lại lên top 1 ai dè ...

Bài viết đã được chỉnh sửa nội dung bởi minhtuyb: 09-04-2012 - 15:52

[minhtuyb]

Đêm nay anh Thế unhide đề hộ em nhé

Đề của MSS09:
Cho tam giác $ABC$ có các đường trung tuyến xuất phát tại đỉnh B và C vuông góc với nhau. Tìm GTNN của biểu thức:
$S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2}$

Đáp án:

*TH 1: Tam giác ABC có 3 góc nhọn:
Với $0^o<\alpha\leq 90^o$, ta có:
$\frac{1}{sin^2\alpha}=\frac{ sin^2\alpha + cos^2\alpha }{sin^2\alpha}=\frac{cos^2\alpha}{ sin^2\alpha}+1=cot^2\alpha +1$
Áp dụng:
$S=\sqrt{3}(\frac{1}{sin^2 ABC}+\frac{1}{sin^2ACB })+\sqrt{2}=\sqrt{3}(cot^2ABC+cot^2ACB+2)+\sqrt{2}$
$\geq \sqrt{3}[\frac{( cotABC+cotACB)^2}{2}+2]+ \sqrt{2}(*)$

Giờ ta tìm GTNN của $cotABC+cotACB$:


-Gọi $AP;BM,CN$ là 2 đường trung tuyến của $\Delta ABC\Rightarrow BM\perp CN(gt)$; G là trọng tâm của $\Delta ABC\Rightarrow \Delta GBC$ vuông tại G
-Kẻ $AH \perp BC (H \in BC)$. Có:
$cotABC+cotACB=\frac{BH}{AH}+\frac{CH}{AH}=\frac{BC}{AH}(1)$
-Theo t/c đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có: $BC=2GP$. Mà $GP=\frac{AP}{3}$ (t/c trọng tâm trong tam giác) $AP\geq AH$ ( Q/hệ giữa đường xiên và hình chiếu). Từ những điều trên, suy ra:
$BC\geq \frac{2}{3}AH(2)$
-Từ (1) và (2)$\Rightarrow cotABC+cotACB\geq \frac{\frac{2}{3}AH }{AH}=\frac{2}{3}(**)$
-Từ (*) và (**) suy ra:
$S\geq \sqrt{3}(\frac{\frac{4}{9}}{2}+2)+ \sqrt{2}=\frac{20}{9}\sqrt{3}+\sqrt{2}=const$
Dấu bằng xảy ra khi $ cotABC=cotACB;H\equiv P\Leftrightarrow \Delta ABC$ cân tại A

*TH 2: Tam giác ABC có góc B hoặc góc C không nhỏ hơn 90 độ.
KMTTQ, giả sử $\widehat{ABC}\geq 90^o>\widehat{ACB}$. Kẻ $AH\perp BC(H\in BC)$
Lúc này ta lại có:
$S=\sqrt{3}(\frac{1}{sin^2 ABC}+\frac{1}{sin^2ACB }) +\sqrt{2}$
$=\sqrt{3}(\frac{1}{\frac{AH^2}{AB^2}}+\frac{1}{\frac{AH^2}{AC^2}})+\sqrt{2}$ (t/c sin 2 góc bù nhau)
$=\sqrt{3}.\frac{AB^2+AC^2}{AH^2}+\sqrt{2}$
Áp dụng đ/l‎ý Py-ta-go vào các tam giác vuông AHB và AHC (vuông tại H), có:
$=\sqrt{3}.\frac{AH^2+HB^2+AH^2+HC^2}{AH^2}+\sqrt{2}=\sqrt{3}.\frac{HB^2+HC^2}{AH^2}+2\sqrt{3}+\sqrt{2}$
Lại có: $ HB^2+HC^2\geq BC^2; BC\geq \frac{2}{3}AH(cmt)$
$\Rightarrow S\geq \sqrt{3}.\frac{\frac{4}{9}AH^2 }{AH^2}+2\sqrt{3}+\sqrt{2}=\frac{22}{9}\sqrt{3}+\sqrt{2}$
Dấu bằng xảy ra khi $H\equiv B$;$H\equiv P\Rightarrow$ dấu bằng không xảy ra

-Từ 2 trường hợp trên ta thấy minS đạt ở TH 1. Vậy
$minS=\frac{20}{9}\sqrt{3}+\sqrt{2}$ khi$\Delta ABC$ nhọn và cân tại A

[Dung Dang Do]

Em ko xét TH tam giác đó vuông rồi tiếc quá

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 11-04-2012 - 21:25

[phantomladyvskaitokid]

thứ nhất, cô giáo t bảo ở THCS chỉ dùng tslg của góc nhọn

thứ hai, t vẫn chưa hiểu tại sao cần xét trường hợp góc B hoặc C tù

@ ĐG: hôm nay ngoan nhỉ

Bài viết đã được chỉnh sửa nội dung bởi phantomladyvskaitokid: 09-04-2012 - 19:12

[minhtuyb]

Em ko xét TH tam giác đó vuông rồi tiếc quá

"*TH 2: Tam giác ABC có góc B hoặc góc C không nhỏ hơn 90 độ."
Bao gồm cả vuông rồi nhé, khi đó $AH=AB;HC=BC;BH=0$. Cả đoạn $HB^2+HC^2\geq BC^2$, có dấu đẳng thức tức là cũng đang xét trường hợp vuông nhé ( "=" xảy ra khi vuông tại B mà )
Thế này thì C-B tính theo bài của bạn Nguyễn Hữu Huy nhé
~~> Phantom: $AB^2+AC^2=5BC^2$ thì sao nhỉ. Chứ hiểu ý bạn lắm, chỉ rõ hộ mình nhé

Bài viết đã được chỉnh sửa nội dung bởi minhtuyb: 09-04-2012 - 19:15

[nthoangcute]

Không cần đâu bạn, cứ cm ra đây rồi để anh Hân gộp cho công bằng

Bạn này khiêu khích mình rùi đấy, nhìn này:
Chứng minh công thức Hê-rông:
Cách 1:Gọi $p$ là nửa chu vi
Giả sử $a \geq b \geq c$. Vẽ đường cao AH ($H \in BC$). Do a là cạnh lớn nhất của tam giác nên B và C là 2 góc nhọn, do đó H nằm giữa B và C.
Đặt $CH = x$ ($x>0$), Áp dụng định lý Py ta go ta có:
$AB^2 - BH^2 = AC^2 - CH^2$ ($=AH^2$),do đó:
$c^2 - (a - x)^2 = b^2 -x^2$ => $2ax = a^2 + b^2 - c^2$
$\to x =\frac{a^2 + b^2 - c^2}{2a}$
Trong tam giác AHC vuông tại H, áp dụng định lý Py-ta-go ta có:
$AH^2 =AC^2 - CH^2 = b^2 - \frac{(a^2 + b^2 - c^2)^2}{4a^2}$
$=\frac{4a^2b^2 -(a^2 + b^2 - c^2)^2}{4a^2}$
Từ đó: $S^2 = (\frac{BC.AH}{2})^2 =\frac{BC^2.AH^2}{4}$
$=\frac{4a^2b^2 - (a^2 + b^2 - c^2)^2}{16}$
$= \frac{(2ab + a^2 + b^2 - c^2)(2ab - a^2 - b^2 + c^2)}{16}$
$=\frac{[(a+b)^2 - c^2][c^2 - (a - b)^2]}{16}$
$=\frac{(a+b+c)(a+b-c)(c+a-b)(c-a+b)}{16}$
$=\frac{2p(2p - 2c)(2p - 2b)(2p - 2a)}{16}$
$= p(p - c)(p - b)(p - c)$

[nthoangcute]

Cách 2:
Ta có: $sin^2 a+cos^2 a=1$
$\to (\frac{2S}{bc})^2+(\frac{b^2+c^2-a^2}{2bc})^2=1$
$\to \frac{16S^2+(b^2+c^2-a^2)^2}{4b^2c^2}=1$
$\to 16S^2=4b^2c^2-(b^2+c^2-a^2)^2$
$\to 16s^2=(2bc-b^2-c^2+a^2)(2bc+b^2+c^2…$
$\to 16S^2=(a^2-(b-c)^2)((b+c)^2-a^2)$
$\to 16S^2=(a-b+c)(a+b-c)(b+c-a)(b+c+a)$
=>$S^2=2p(2p-2c)(2p-2b)(2p-2a)/16$
=>$S^2=p(p-c)(p-a)(p-b)$

Bài viết đã được chỉnh sửa nội dung bởi nthoangcute: 09-04-2012 - 20:34

[NLT]

Mời mấy anh chấm điểm bài thi lần này

[NLT]

Đêm nay anh Thế unhide đề hộ em nhé

Đề của MSS09:
Cho tam giác $ABC$ có các đường trung tuyến xuất phát tại đỉnh B và C vuông góc với nhau. Tìm GTNN của biểu thức:
$S=\frac{\sqrt{3}}{sin^2ABC}+\frac{\sqrt{3}}{sin^2ACB}+\sqrt{2}$

Không hiểu sao mà minhtuyb lại cho đề có số $\sqrt{2}$ không có gì đặc biệt vào vậy ? Và dẫn đến kết quả cuối cùng khi cộng thêm $\sqrt{2}$ mất đẹp mất. Mình nghĩ là những trường hợp như vậy các bạn ko nên đưa vào, càng làm cho bài toán mất đẹp hơn