Chủ đề này có 7 trả lời

[Tham Lang]

Mình xin được đăng một chuyên đề nhỏ của thầy giáo dạy mình, đã được đăng lên nội san nhà trường.
Sau đây là nội dung

TƯ DUY TÌM TÒI BÀI TOÁN VÀ CÁCH GIẢI QUYẾT MỘT VẤN ĐỀ

Thầy giáo Nguyễn Đức Thịnh - THPT Bắc Yên Thành - Nghệ An

Chúng ta bắt đầu từ bài toán sau :
Cho tam giác $ABC$ đều cạnh $a$, khi đó tam giác $ABC$ có diện tích $S$ được tính theo công thức :
$S = \dfrac{\sqrt{3}a^2}{4}$ suy ra $3a^2 = 4\sqrt{3}S$, tức là $a^2 + a^2+a^2 = 4\sqrt{3}S$,vậy nảy sinh một vấn đề với một tam giác bất kì thì ta có kết quả như thế nào ?
Đi đến bài toán :
Cho tam giác $ABC$ có các cạnh $a,b,c$ và diện tích $S$.Chứng minh rằng :
$$a^2+b^2+c^2\ge4\sqrt{3}S (1)$$
Thực tế lời giải bài toán đã được trình bày ở nhiều tài liệu tham khảo, tuy nhiên mục đích ở chuyên đề này là hướng dẫn học sinh chứng minh theo nhiều cách khác nhau nhằm rèn luyện tính linh hoạt của tư duy đồng thời các phương pháp chứng minh đó còn dùng cho các bài toán khác. Sau đây là một số cách chứng minh (1) Đẳng thức xảy ra khi tam giác $ABC$ đều ..
Cách giải 1.Sử dụng công thức $Herong$ và bất đẳng thức $AM-GM$
ÁP dụng công thức $Herong$ :
$$S^2 = p(p-a)(p-b)(p-c) \le p\left (\dfrac{p-a+p-b+p-c}{3}\right )^2 = \left (\dfrac{a+b+c}{6}\right )^3$$
Do đó :$12\sqrt{3}S \le (a+b+c)^2 \le 3\left (a^2+b^2+c^2\right ) \Leftrightarrow a^2+b^2+c^2 \ge4\sqrt{3}S$$
Bài toán được chứng minh.
Cách giải 2.Sử dụng định lí $côsin$ và bất đẳng thức $Cauchy-Schwarz$ :
Áp dụng định lí $côsin$ :$c^2 = a^2 + b^2 - 2ab\cos{C}$ và công thức tính diện tích tam giác $S = \dfrac{ab\sin{C}}{2}$, ta có :
$$(1) \Leftrightarrow a^2 + b^2 + a^2 + b^2 - 2ab\cos{C} \ge 2\sqrt{3}ab\sin{C} \Leftrightarrow a^2 + b^2 \ge ab\cos{C} + ab\sin{C} \Leftrightarrow \dfrac{a}{b}+\dfrac{b}{a} \ge \cos{C} = \sqrt{3}\sin{C} (1')$$
$(1')$ đúng vì $VT \ge 2, VP \le \sqrt{4.(\sin^2{C}+\cos^2{C})} = 2$$
Cách giải 3 . Sử dụng công thức cộng cung và định lí $côsin$ :
ÁP dụng định lí $côsin$ :$c^2 = a^2+b^2-2ab\cos{C}$ và công thức tính diện tích tam giác $S = \dfrac{ab\sin{C}}{2}$, ta có :
$$(1) \Leftrightarrow a^2+b^2-ab\cos{C} - \sqrt{3}ab\sin{C} \ge 0 \Leftrightarrow (a-b)^2-2ab\left [1 - \left (\dfrac{1}{2}\cos{C}+\dfrac{\sqrt{3}}{2}\sin{C}\right ) \right ] \ge 0$$
$$\Leftrightarrow (a - b)^2+2ab\left [1 -\cos{(C - 60^0)}\right ] \ge 0$$
Đúng vì $(a - b)^2 \ge 0, \cos{(C - 60^0)}\le 1$
Cách 4.sử dụng cách dựng hình và công thức cộng cung.
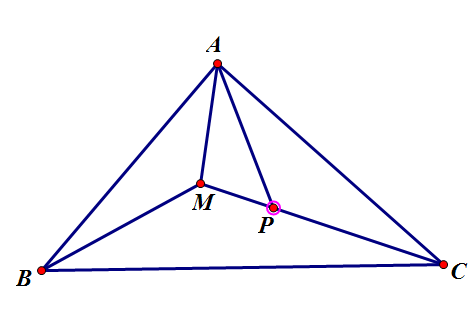
Trong trường hợp tam giác $ABC$ đều thì (1) đúng. Xét trường hợp tam giác $ABC$ không đều , ta có thể coi góc $A$ lớn nhất, suy ra $A >60^0$,dựng vào phía trong tam giác $ABC$ các tam giác cân $AMB, APC$ sao cho :$\hat{AMB} = \hat{APC} = 120^0$.
Khi đó :$AM = \dfrac{c}{\sqrt{3}}, AP = \dfrac{b}{\sqrt{3}}$ .ÁP dụng định lí $côsin$ trong $\bigtriangleup{MAP}$, ta có :
$$MP^2 =AM^2+AP^2-2AM.AP.\cos{MAP} = \left (\dfrac{b}{\sqrt{3}}\right )^2 +\left (\dfrac{c}{\sqrt{3}}\right )^2 -\dfrac{2bc\cos{(A -60^0)}}{3}$$
Nên $$MP^2=\dfrac{b^2+c^2-2bc\cos{(A-60^0)}}{3}=\dfrac{b^2+c^2-bc\left (\cos{A}+\sqrt{3}\sin{A}\right )}{3}=\dfrac{a^2+b^2+c^2-4\sqrt{3}S}{6}$$
Mặt khác $MP^2 \ge 0 \Leftrightarrow a^2+b^2+c^2\ge4\sqrt{3}S$.
Cách giải 5.Sử dụng bất đẳng thức phụ và công thức $Herong$.
Ta có $a^2\ge a^2-(b-c)^2=4(p-b)(p-c)$
Suy ra $a^2+b^2+c^2 \ge 4\left ((p-a)(p-b)+(p-b)(p-c)+(p-c)(p-a)\right ) $
Sử dụng $(xy+yz+zx)^2\ge3xyz(x+y+z)$
Ta có :
$a^2+b^2+c^2\ge\sqrt{3xyz(x+y+z)}=4\sqrt{3}S$
Cách giải 6.Sử dụng công thức về cạnh và bán kính đường tròn ngoại tiếp.
Dễ chứng minh $a^2+b^2+c^2\le 9R^2$ bằng phương pháp $vecto$.
ÁP dụng $AM-GM$ ta có :$9R^2 \ge a^2+b^2+c^2 \ge3\sqrt[3]{a^2b^2c^2}\Leftrightarrow abc\le3\sqrt{3}R^3
\Leftrightarrow a^2+b^2+c^2\ge 3\sqrt[3]{a^2b^2c^2}=\dfrac{3abc}{\sqrt[3]{abc}}\ge\dfrac{\sqrt{3}abc}{R}\ge4\sqrt{3}S$
Cách giải 7.Sử dụng định lí $cosin$ mở rộng và đẳng thức lượng giác.
ÁP dụng định lí $côsin$ mở rộng, ta có :
$\cot{A}+\cot{B}+\cot{C}=\dfrac{a^2+b^2+c^2}{4S}$
Lại có :
$\cot{A}\cot{B}+\cot{B}\cot{C}+\cot{C}\cot{A}=1$ nên suy ra $\cot{A}+\cot{B}+\cot{C}\sqrt{3}$.suy ra
$a^2+b^2+c^2\ge 4\sqrt{3}S$.
Cách giải 8.Sử dụng bất đẳng thức lượn giác và $AM-GM$.
Áp dụng định lí sin và công thức tính diện tích $S = 2R^2\sin{A}\sin{B}\sin{C}$, ta có :
$(1)\Leftrightarrow\sin^2{A}+\sin^2{B}+\sin^2{C}\ge2\sqrt{3}\sin{A}\sin{B}\sin{C}$
Theo AM-GM, ta có :
$\sin^2{A}+\sin^2{B}+\sin^2{C}\ge 3\sqrt[3]{\sin^2{A}\sin^2{B}\sin^2{C}}=\dfrac{3\sin^2{A}\sin^2{B}\sin^2{C}}{\sqrt{\sin^2{A}\sin^2{B}\sin^2{C}}}$
Mặt khác, áp dụng $AM-GM$ ta lại có :
$\sqrt{\sin^2{A}\sin^2{B}\sin^2{C}}\le\dfrac{3\sqrt{3}}{8}$ nên $\sin^2{A}+\sin^2{B}+\sin^2{C}\ge2\sqrt{3}\sin{A}\sin{B}\sin{C}$
Bất đẳng thức được chứng minh.
Cách giải 9.Sử dụng cách kẻ đường cao và $AM-GM$
Giả sử góc $A$ là lớn nhất.Kẻ đường cao $AH$, khi đó :
$AB^2 =AH^2+BH^2, AC^2=AH^2+CH^2$ nên $a^2+b^2+c^2=AB^2+AC^2+BC^2 =2AH^2+BH^2+CH^2+BC^2 \ge 2AH^2+\dfrac{BC^2}{2}+BC^2=2AH^2+\dfrac{3BC^2}{2}\ge2\sqrt{3}AH.BC=4\sqrt{3}S.$
Cách giải 10.Sử dụng công thức đường trung tuyến và bất đăng thức $AM-GM$
Áp dụng công thức đường trung tuyến $b^2+c^2=2m_a^2+\dfrac{a^2}{2}\Leftrightarrow a^2+b^2+c^2=2m_a^2+\dfrac{3a^2}{2}\ge 2\sqrt{3}a.m_a\ge2\sqrt{3}a.h_a=4\sqrt{3}S$
Từ những gợi ý trên, ta hoàn toàn có thể đưa ra được những cách giải khác cho bài toán này.

[icefrogblug]

hay thiet

[CD13]

Chém bừa thêm 5 cách nữa vậy!

Cách 1
$\tan \frac{A}{2}.\tan \frac{B}{2}.\tan \frac{C}{2} \le \frac{1}{3\sqrt{3}}$
$ \to a^2+b^2+c^2 \ge \frac{(a+b+c)^2}{3}=4\sqrt{3}\frac{p^2}{3\sqrt{3}} \ge 4\sqrt{3}(p^2.\tan \frac{A}{2}.\tan \frac{B}{2}.\tan \frac{C}{2})=4\sqrt{3}S$


Cách 2:
Giả sử $a \ge b \ge c \to \sin A \ge \sin B \ge \sin C$
Ta có:
$(a^2+b^2+c^2)\frac{3\sqrt{3}}{2} \ge (ab+bc+ca)\frac{3\sqrt{3}}{2} \ge (ab+bc+ca)(\sin A+\sin B+\sin C)\\ \ge 3(bc\sin A+ac\sin B+ab\sin C)=18S $
$\to$ điều phải chứng minh!

Cách 3:
Hêrông cho ta viết được: $16S^2=2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)$
từ: $a^4+b^4+c^4 \ge a^2b^2+b^2c^2+c^2a^2$
dẫn đến $(a^2+b^2+c^2)^2\ge 3[2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)]=48S^2$

Cách 4:
Chứng minh: $a^2+b^2+c^2\ge ab+bc+ca \ge 36r^2$
Lại do: $a^2+b^2+c^2\ge \frac{4}{3}p^2$
Nhân 2 vế BĐT cùng chiều cho ta điều phải chứng minh!

Cách 5: (Một bài toán quen thuộc)
Chứng minh: $a^2+b^2+c^2\ge 4\sqrt{3}S+(a-b)^2+(b-c)^2+(c-a)^2$

Bài viết đã được chỉnh sửa nội dung bởi CD13: 20-08-2012 - 18:14

[CD13]

Và chúng ta có mấy bài toán bậc cao hơn tí!

Bài 1:
$a^n+b^n+c^n \ge \frac{(2\sqrt{S})^n}{\sqrt[4]{3^{n-4}}}$

Bài 2:
$a^nb^n+b^nc^n+c^na^n \ge 4^n \sqrt{3^{2-n}}S^n$

Bài 3:
$a^{2n}+b^{2n}+c^{2n} \ge 3(\frac{4S}{\sqrt{3}})^n+(a-b)^{2n}+(b-c)^{2n}+(c-a)^{2n}$.

Bài viết đã được chỉnh sửa nội dung bởi CD13: 20-08-2012 - 18:24

[yenyen100]

Ô,bạn học trg Bắc Yên Thành à,mình cung ở Yên Thành nhưng lại ở Đô Thành nên pải đi Diễn Châu học nè,Mình rất mong được sự chỉ giáo của các bạn ,bởi vì mình biết gv trên đó rất giỏi,tiếc là m k có cơ hội dc lên đó học tập

[thanh hai nguyen]

tuy biết tư duy là như vậy nhưng những bài trên có hướng giải phần lớn do có sẵn và tự nội suy tư duy chứ chẳng may đi thi gặp bài khó mình vẫn ? như thường, nhưng nó vẫn very hay, thanks!

[phanquockhanh]

Mình xin được đóng góp một bài tập nhỏ cho chuyên đề trên:

Bài toán:  Cho $\Delta ABC$, chứng minh rằng:

$cosA+cosB+cosC\leq \frac{3}{2}$

Bài giải:

Cách 1:Dùng tỉ số diện tích

Kẻ các đường cao AD,BE,CF 

Đặt $S_{AEF}=S_{1};S_{BFD}=S_{2};S_{CED}=S_{3},S_{ABC}=S$.

Khi đó: $cosA=\sqrt{\frac{S_{1}}{S}};cosB=\sqrt{\frac{S_{2}}{S}};cosC=\sqrt{\frac{S_{3}}{S}}$

$\sqrt{\frac{S_{1}}{S}}=\sqrt{\frac{AF.AE}{AB.AC}}\leq \frac{1}{2}\left ( \frac{AF}{AB}+\frac{AE}{AC} \right ) (1)$

Tương tự:$\sqrt{\frac{S_{2}}{S}}=\leq \frac{1}{2}\left ( \frac{BF}{AB}+\frac{BD}{BC} \right ) (2)$

 

$\sqrt{\frac{S_{3}}{S}}=\leq \frac{1}{2}\left ( \frac{CD}{CB}+\frac{CE}{CA} \right ) (3)$

CỘNG (1),(2),(3) THEO TỪNG VẾ TA ĐƯỢC:

$cosA+cosB+cosC\leq \frac{1}{2}\left ( \frac{AF}{AB} +\frac{FB}{AB}+ \frac{AE}{AC} +\frac{EC}{AC} +\frac{BD}{BC} +\frac{DC}{BC} \right )=\frac{3}{2}$

Đẳng thức xảy ra $\Leftrightarrow$ ABC đều

Cách 2:Vận dụng bất đẳng thức Erdos-Mordell:

Cho tam giác ABC.M là điểm bất kì nămg trong tam giác.Đặt $x_{1}=MA;x_{2}=MB;x_{2}=MC;p_{1},p_{2},p_{3}$ lần lượt là khoảng cách từ điểm M đến BC,CA,AB tương ứng. Khi đó ta có bất đẳng thức:

$x_{1}+x_{2}+x_{3}\geq 2(p_{1}+p_{2}+p_{3})$

Áp dụng :

Gọi O,R lần lượt là tâm và bán kính đường tròn ngoại tiếp tam giác ABC.

Gọi M,N,P lần lượt là trung điểm các cạnh AB,BC,CA

Nhận thấy $\widehat{A}=\widehat{MOB}$

Do đó:

$cosA=cos\widehat{MOB}=\frac{OM}{OB}=\frac{OM}{R};cosB=\frac{ON}{R};cosC=\frac{OP}{R}$

Do đó:

$cosA+cosB+cosC=\frac{OM+ON+OP}{R}\leq \frac{1}{2}\left ( \frac{OA+OB+OC}{R} \right )=\frac{3}{2}(ERDOS-MORDELL)$

Đẳng thức xảy ra $\Leftrightarrow$ ABC đều

Cách 3:Sử dụng bất đẳng thức Trê-bư-sêp:

Gọi a,b,c là 3 cạnh tam giác ABC.Khi đó:

a=c.cosB+b.cosC

b=a.cosC+c.cosB;

c=a.cosB+b.cosA.

Cộng 3 bất đẳng thức trên ta có:

$a+b+c=(c+b)cosA+(a+c)cosB+(a+b)cosC$

Không mất tính tổng quát giả sử:$a\geq b\geq c$.Khi đó:

$\left\{\begin{matrix} cosA\leq cosB\leq cosC\\ c+b\leq a+c\leq a+b \end{matrix}\right.$

Do đó:

$a+b+c=(c+b)cosA+(a+c)cosB+(a+b)cosC$

$\geq \frac{1}{3}(cosA+cosB+cosC)(c+b+a+c+a+b)$(TRE-BU-SEP)

$\Rightarrow \frac{1}{3}(cosA+cosB+cosC)\leq \frac{3}{2}$

Cách 4:Phương pháp vectơ:

Gọi I,r lần lượt là tâm và bán kính đường tròn nội tiếp tam giác ABC.M, N, P lần lượt là tiếp điểm của đường tròn với các cạnh AB,AC,BC.Khi đó, ta có:

$0\leq (\overrightarrow{IM}+\overrightarrow{IN}+\overrightarrow{IP})^{2}$

$\Leftrightarrow0\leq3r^2+2(\overrightarrow{IM}.\overrightarrow{IN}+\overrightarrow{IM}.\overrightarrow{IP}+\overrightarrow{IP}.\overrightarrow{IN})$

Mặt khác:

$\overrightarrow{IM}.\overrightarrow{IN}=2r^2cos\widehat{MIN}=-2r^2.cosA$

Tương tự:

$\overrightarrow{IM}.\overrightarrow{IP}=-2r^2.cosB; \overrightarrow{IP}.\overrightarrow{IN}=-2r^2.cosC;$

Do đó:

$cosA+cosB+cosC\leq \frac{3}{2}$

Đẳng thức xảy ra <=> Tam giác ABC đều.

 

Bài viết đã được chỉnh sửa nội dung bởi phanquockhanh: 27-05-2013 - 15:30

[phanquockhanh]

Cách 5: Sử dụng vector gốc

Lấy A,B,C lần lượt là ba gốc của 3 vectơ đơn vị sau:

$\overrightarrow{e_{1}}=\frac{\overrightarrow{AB}}{AB}$

$\overrightarrow{e_{2}}=\frac{\overrightarrow{BC}}{BC}$

$\overrightarrow{e_{3}}=\frac{\overrightarrow{CA}}{CA}$

Ta có: $0\leq (\overrightarrow{e_{1}}+\overrightarrow{e_{2}}+\overrightarrow{e_{3}})^2$

$\Leftrightarrow 0\leq 3+2(\overrightarrow{e_{1}}\overrightarrow{e_{2}}+\overrightarrow{e_{2}}\overrightarrow{e_{3}}+\overrightarrow{e_{3}}\overrightarrow{e_{1}})$

$\Leftrightarrow 0\leq 3-2(cosA+cosB+cosC)$

$\Leftrightarrow cosA+cosB+cosC\leq \frac{3}{2}$

Dấu "=" xảy ra <=> $\Delta$ ABC đều

Cách 6:Sử dụng bất đẳng thức SCHUR:

Ta có:

cosA+cosB+cosC$\leq \frac{3}{2}$$\Leftrightarrow \frac{b^2+c^2-a^2}{2bc}+\frac{a^2+c^2-b^2}{2ac}+\frac{a^2+b^2-c}{2ab}$

$\Leftrightarrow b^2a+c^2a+c^2b+a^2b+a^2c+b^2c\leq 3abc$

$\Leftrightarrow a(a-b)(a-c)+b(b-c)(b-a)+c(c-a)(c-b)\geq 0$

(Bất đẳng thức Schur)

Cách 7:Sử dụng tam thức bâc 2:

Xét $cosA+cosB+cosC-\frac{3}{2}=$

$2cos\frac{A+B}{2}cos\frac{A-B}{2}+1-2sin^{2}\frac{C}{2}-\frac{3}{2}=$

$2sin\frac{C}{2}cos\frac{A-B}{2}-2sin^2\frac{C}{2}-\frac{1}{2}$

Đặt $x=sin\frac{C}{2}.(0< x<1)$.Xét tam thức $f(x)=-2sin^{2}x+2cos\frac{A-B}{2}x-\frac{1}{2}$

Ta có: $\Delta '=cos^{2}\frac{A-B}{2}-1\leq 0;a=-2< 0 \Rightarrow f(x)\leq 0,\forall x$(0< x<1)

Từ đó: $cosA+cosB+cosC\leq \frac{3}{2}$

Cách 8:dùng phương pháp hàm số

Ta có:

$cosA+cosB+cosC=2cos\frac{A+B}{2}cos\frac{A-B}{2}+1-2sin^{2}\frac{C}{2}$

Đặt x=sin$\frac{C}{2}$(0<x<1)

Xét hàm số:$f(x)=-2x^{2}+2cos\frac{A-B}{2}x+1$

Lập BBT,ta được:

$f(x)\leq f_{max}(x)=1+\frac{1}{2}cos\frac{A-B}{2}\leq \frac{3}{2}$

Từ đó, ta có ĐPCM

 

Bài viết đã được chỉnh sửa nội dung bởi phanquockhanh: 27-05-2013 - 15:37